红黑树（C++）

文章目录

红黑树

红黑树的概念

红黑树的概念 红黑树，是一种二叉搜索树，但在每个结点上增加一个存储位表示结点的颜色，可以是Red或Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制，红黑树确保没有一条路径会比其他路径长出俩倍，因而是接近平衡的。

红黑树和AVL树都是高效的平衡二叉树，增删改查的时间复杂度都是O()，红黑树不追求绝对平衡，其只需保证最长路径不超过最短路径的2倍，相对而言，降低了插入和旋转的次数，所以在经常进行增删的结构中性能比AVL树更优，而且红黑树实现比较简单，所以实际运用中红黑树更多。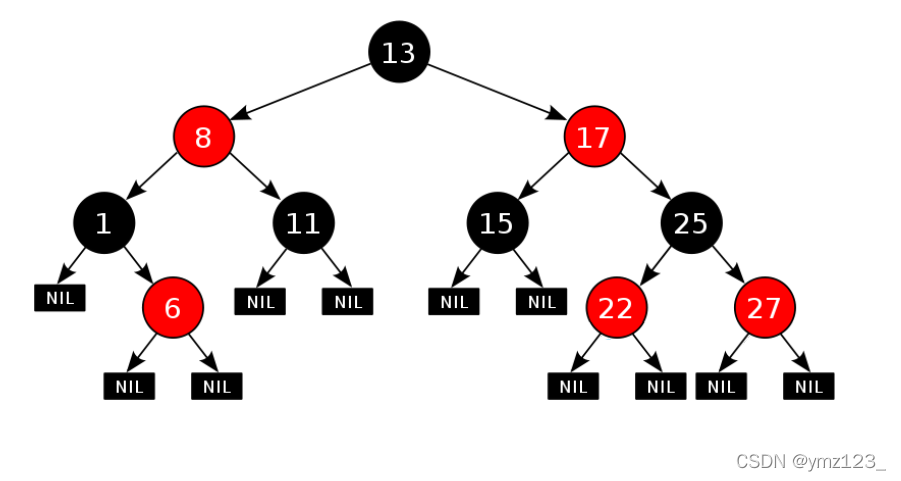

红黑树的性质

1. 每个结点不是红色就是黑色
2. 根节点是黑色的
3. 如果一个结点是红色的，则它的两个孩子结点是黑色的
4. 对于每个结点，从该节点到其所有后代叶节点的简单路径上，均包含相同数目的黑色结点
5. 每个叶子结点都是黑色的（此处的叶子节点指的是空结点，如上图路径数为11条）

红黑树结点的定义

enumColor{
    BLACK,
    RED
};template<classT>structRBTreeNode{
    RBTreeNode<T>* _left;
    RBTreeNode<T>* _right;
    RBTreeNode<T>* _parent;

    Color _col;
    T _data;RBTreeNode(const T& data):_left(nullptr),_right(nullptr),_parent(nullptr), _col（RED)
        ，_data(data){}};

红黑树的插入操作

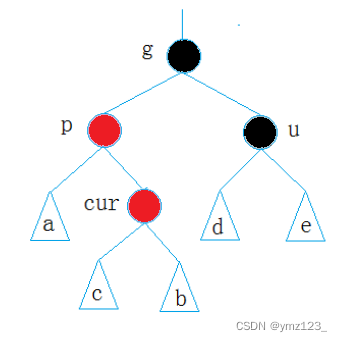
约定：cur为当前节点，p为父节点，g为祖父节点，u为叔叔节点

情况一

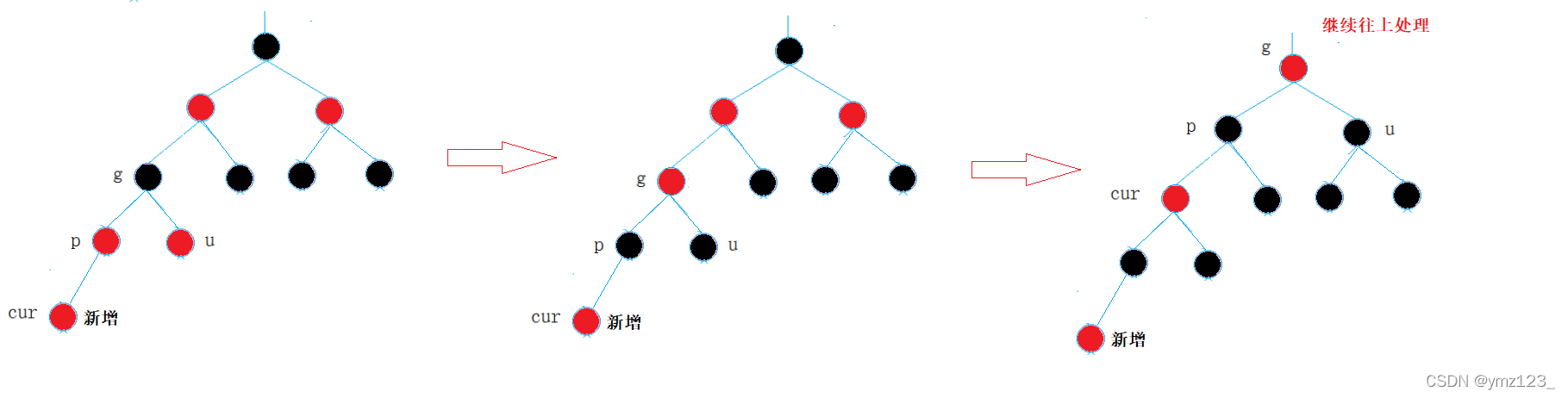
• 情况一：cur为红，p为红，g为黑，u存在且为红 注意：此处看到的树，可能是一棵完整的树，也可能是一棵子树
• 解决方式：将p，u改为黑，g改为红，然后把g当成cur，继续向上调整

如果g是根节点，调整完成后，需要将g改为黑色
如果g是子树，g一定有双亲，且g的双亲如果是红色，需要继续向上调整。

情况二

• 情况二：cur为红，p为红，g为黑，u不存在/u为黑
• 解决方法：p为g的左孩子，cur为p的左孩子，则进行右单旋；p为g的右孩子，cur为p的右孩子，则进行左单旋。 p变黑，g变红。

1.如果u节点不存在，则cur一定是新插入节点，因为如果cur不是新插入节点，则cur和p一定有一个节点的颜色是黑色，就不满足性质4：每条路径黑色节点个数相同。

2.如果u节点存在，则其一定是黑色的，cur一定不是新增节点，那么cur节点原来的颜色一定是黑色的，是作为子树的祖父，由第一种情况变化过来的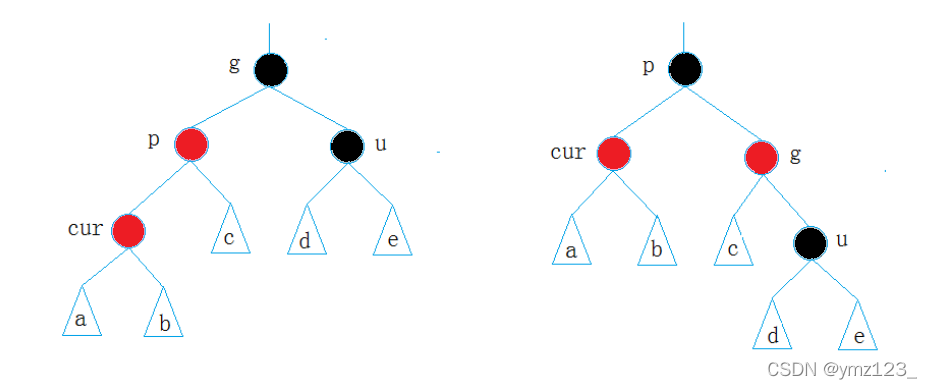

情况三

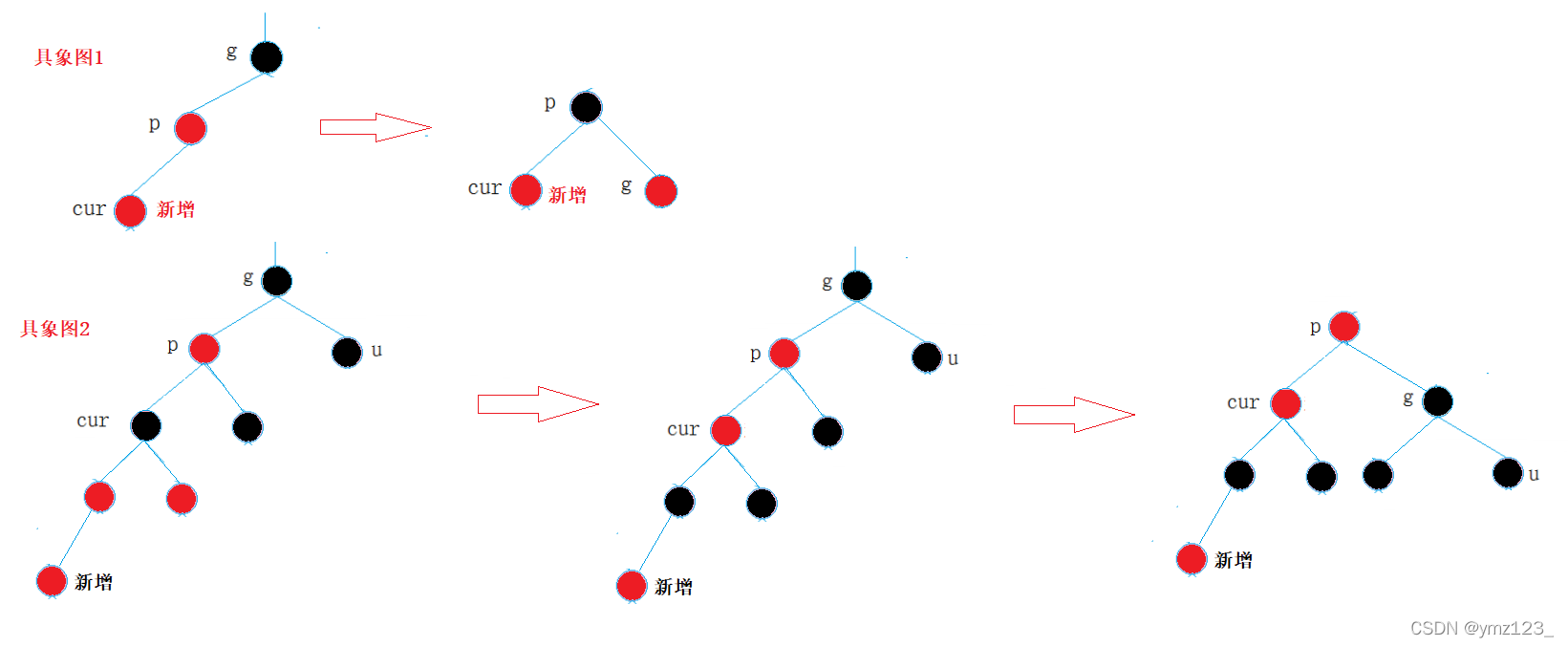
• 情况三：cur为红，p为红，g为黑，u不存在/u为黑（折线型）
• p为g的左孩子，cur为p的右孩子，则针对p做左单旋转； p为g的右孩子，cur为p的左孩子，则针对p做右单旋转。 即转换为了情况二。再对g做对于旋转。 即进行双旋转。

// T->K  set// T->pair<const K, V> maptemplate<classK,classT,classKeyOfT>classRBTree{typedef RBTreeNode<T> Node;public:typedef RBTreeIterator<T, T&, T*> iterator;typedef RBTreeIterator<T,const T&,const T*> const_iterator;

    iterator begin();
    iterator end();RBTree():_root(nullptr){}// 拷贝构造和赋值重载// 析构

    Node*Find(const K& key);

    pair<iterator,bool>Insert(const T& data){if(_root ==nullptr){
            _root =newNode(data);
            _root->_col = BLACK;returnmake_pair(iterator(_root),true);}

        Node* parent =nullptr;
        Node* cur = _root;

        KeyOfT kot;while(cur){if(kot(cur->_data)<kot(data)){
                parent = cur;
                cur = cur->_right;}elseif(kot(cur->_data)>kot(data)){
                parent = cur;
                cur = cur->_left;}else{returnmake_pair(iterator(cur),false);}}// 新增节点，颜色是红色，可能破坏规则3，产生连续红色节点
        cur =newNode(data);
        Node* newnode = cur;
        cur->_col = RED;if(kot(parent->_data)<kot(data)){
            parent->_right = cur;
            cur->_parent = parent;}else{
            parent->_left = cur;
            cur->_parent = parent;}// 控制近似平衡while(parent && parent->_col == RED){
            Node* grandfather = parent->_parent;if(parent == grandfather->_left){
                Node* uncle = grandfather->_right;// 情况一：uncle存在且为红，进行变色处理，并继续往上更新处理if(uncle && uncle->_col == RED){
                    parent->_col = uncle->_col = BLACK;
                    grandfather->_col = RED;

                    cur = grandfather;
                    parent = cur->_parent;}// 情况二+三：uncle不存在，或者存在且为黑，需要旋转+变色处理else{// 情况二：单旋+变色if(cur == parent->_left){RotateR(grandfather);
                        parent->_col = BLACK;
                        grandfather->_col = RED;}else// 情况三：双旋 + 变色{RotateL(parent);RotateR(grandfather);
                        cur->_col = BLACK;
                        grandfather->_col = RED;}break;}}else// (parent == grandfather->_right){
                Node* uncle = grandfather->_left;if(uncle && uncle->_col == RED){
                    parent->_col = uncle->_col = BLACK;
                    grandfather->_col = RED;

                    cur = grandfather;
                    parent = cur->_parent;}else{if(parent->_right == cur){RotateL(grandfather);
                        parent->_col = BLACK;
                        grandfather->_col = RED;}else{RotateR(parent);RotateL(grandfather);
                        cur->_col = BLACK;
                        grandfather->_col = RED;}break;}}}

        _root->_col = BLACK;returnmake_pair(iterator(newnode),true);}voidRotateR(Node* parent);voidRotateL(Node* parent);private:
    Node* _root;};

红黑树的验证

红黑树的检测分为两步：

1. 检测其是否满足二叉搜索树(中序遍历是否为有序序列)
2. 检测其是否满足红黑树的性质

此处用未改造过的红黑树

template<classK,classV>structRBTreeNode{
    RBTreeNode<K, V>* _left;
    RBTreeNode<K, V>* _right;
    RBTreeNode<K, V>* _parent;

    Colour _col;
    pair<K, V> _kv;RBTreeNode(const pair<K, V>& kv):_left(nullptr),_right(nullptr),_parent(nullptr),_col(RED),_kv(kv){}};template<classK,classV>classRBTree{typedef RBTreeNode<K, V> Node;public:RBTree():_root(nullptr){}boolInsert(const pair<K, V>& kv);voidRotateR(Node* parent);voidRotateL(Node* parent);void_InOrder(Node* root){if(root ==nullptr){return;}_InOrder(root->_left);
        cout << root->_kv.first <<" ";_InOrder(root->_right);}voidInOrder(){_InOrder(_root);
        cout<<endl;}boolCheckRED_RED(Node* cur){if(cur ==nullptr){returntrue;}if(cur->_col == RED && cur->_parent->_col == RED){
            cout <<"违反规则三，存在连续的红色节点"<< endl;returnfalse;}returnCheckRED_RED(cur->_left)&&CheckRED_RED(cur->_right);}// 检查每条路径黑色节点的数量boolCheckBlackNum(Node* cur,int blackNum,int benchmark){if(cur ==nullptr){if(blackNum != benchmark){
                cout <<"违反规则四：黑色节点的数量不相等"<< endl;returnfalse;}returntrue;}if(cur->_col == BLACK)++blackNum;returnCheckBlackNum(cur->_left, blackNum, benchmark)&&CheckBlackNum(cur->_right, blackNum, benchmark);}boolIsBalance(){if(_root ==nullptr){returntrue;}if(_root->_col == RED){
            cout <<"根节点是红色，违反规则二"<< endl;returnfalse;}// 算出最左路径的黑色节点的数量作为基准值int benchmark =0;
        Node* cur = _root;while(cur){if(cur->_col == BLACK){++benchmark;}

            cur = cur->_left;}int blackNum =0;returnCheckRED_RED(_root)&&CheckBlackNum(_root, blackNum, benchmark);}private:
    Node* _root;};voidTestRBTree1(){constint n =1000000;
    vector<int> a;
    a.reserve(n);srand(time(0));for(size_t i =0; i < n;++i){
        a.push_back(rand());}

    RBTree<int,int> t1;for(auto e : a){
        t1.Insert(make_pair(e, e));}

    cout << t1.IsBalance()<< endl;//t1.InOrder();}

用红黑树封装map、set

红黑树的迭代器

begin()与end()
begin()可以放在红黑树中最小节点(即最左侧节点)的位置
end()放在最大节点(最右侧节点)的下一个位置

typedef RBTreeIterator<T, T&, T*> iterator;typedef RBTreeIterator<T,const T&,const T*> const_iterator;

    iterator begin(){
        Node* left = _root;while(left && left->_left){
            left = left->_left;}//return leftreturniterator(left);}

    iterator end(){returniterator(nullptr);}

操作符重载

template<classT,classRef,classPtr>structRBTreeIterator{typedef RBTreeNode<T> Node;typedef RBTreeIterator<T, Ref, Ptr> Self;
    Node* _node;RBTreeIterator(Node* node =nullptr):_node(node){}

    Ref operator*(){return _node->_data;}

    Ptr operator->(){return&_node->_data;}

    Self&operator--(){// 跟++基本是反过来return*this;}

    Self&operator++(){if(_node->_right){// 右子树中序第一个节点，也就是右子树的最左节点
            Node* subLeft = _node->_right;while(subLeft->_left){
                subLeft = subLeft->_left;}

            _node = subLeft;}else{// 当前子树已经访问完了，要去找祖先访问，沿着到根节点的路径往上走，// 找孩子是父亲左的那个父亲节点
            Node* cur = _node;
            Node* parent = cur->_parent;while(parent && parent->_right == cur){
                cur = parent;
                parent = parent->_parent;}

            _node = parent;}return*this;}booloperator!=(const Self& s)const{return _node != s._node;}booloperator==(const Self& s)const{return _node == s._node;}};

封装map

#pragmaonce#include"RBTree.h"namespace MyMap
{template<classK,classV>classmap{structMapKeyOfT{const K&operator()(const pair<const K, V>& kv){return kv.first;}};public:typedeftypenameRBTree<K, pair<const K, V>, MapKeyOfT>::iterator iterator;

        iterator begin(){return _t.begin();}

        iterator end(){return _t.end();}

        pair<iterator,bool>insert(const pair<const K, V>& kv){return _t.Insert(kv);}

        V&operator[](const K& key){
            pair<iterator,bool> ret = _t.Insert(make_pair(key,V()));return ret.first->second;}private:
        RBTree<K, pair<const K, V>, MapKeyOfT> _t;};voidtest_map(){
        map<string, string> dict;
        dict.insert(make_pair("sort","排序"));
        dict.insert(make_pair("string","字符串"));
        dict.insert(make_pair("debug","找虫子"));
        dict.insert(make_pair("set","集合"));

        map<string, string>::iterator it = dict.begin();while(it != dict.end()){
            cout << it->first <<":"<< it->second << endl;++it;}
        cout << endl;}}

封装set

#pragmaonce#include"RBTree.h"namespace MySet
{template<classK>classset{structSetKeyOfT{const K&operator()(const K& key){return key;}};public:typedeftypenameRBTree<K, K, SetKeyOfT>::iterator iterator;

        iterator begin(){return _t.begin();}

        iterator end(){return _t.end();}

        pair<iterator,bool>insert(const K& key){return _t.Insert(key);}private:
        RBTree<K, K, SetKeyOfT> _t;};voidtest_set(){
        set<int> s;
        s.insert(1);
        s.insert(3);
        s.insert(7);
        s.insert(2);
        s.insert(12);
        s.insert(22);
        s.insert(2);
        s.insert(23);
        s.insert(-2);
        s.insert(-9);
        s.insert(30);

        set<int>::iterator it = s.begin();while(it != s.end()){
            cout <<*it <<" ";++it;}
        cout << endl;for(auto e : s){
            cout << e <<" ";}
        cout << endl;}}