机器学习——先验概率、后验概率、全概率公式、贝叶斯公式

一、先验概率

1、定义

先验概率（prior probability）是指根据以往经验和分析得到的概率，如全概率公式，它往往作为"由因求果"问题中的"因"出现的概率。——百度百科

2、直观理解

这件事还没有发生，根据以往的经验和数据推断出这件事会发生的概率。

3、例子

以扔硬币为例，在扔之前就知道正面向上的概率为0.5，这个0.5就是先验概率。

二、后验概率

1、定义

后验概率是指在得到“结果”的信息后重新修正的概率，是“执果寻因”问题中的"果"。——百度百科

2、直观理解

这件事已经发生，但是导致这件事发生的原因可能有多种，此时推断是由哪一种原因导致的，计算这件事发生的原因是由某个因素引起的概率。

3、例子

小明同学不去学校上课，有两个原因：一是生病，二是自行车坏了。 然后，今天上课的时候老师发现小明同学没来学校，（注：这里是一个结果。 也就是说，小明同学没来学校这件事已经发生了。）此时，老师叫同学们计算小明同学没来学校是因为生病还是自行车坏了的概率。

这里已经发生的事是小明同学没有来学校上课。 原因有两个：是生病和自行车坏了。后验概率就是根据结果（小明没来学校）来计算原因（生病/自行车坏了）的概率。

三、全概率公式

全概率公式为概率论中的重要公式，它将对一复杂事件A的概率求解问题转化为了在不同情况下发生的简单事件的概率的求和问题。——百度百科

内容：如果事件B1、B2、B3…Bi构成一个完备事件组，即它们两两互不相容，其和为全集；并且P(Bi)大于0，则对任一事件A有

全概率公式：P(A)=P(A|B1)P(B1) + P(A|B2)P(B2) + ... + P(A|Bi)P(Bi)。

全概率就是表示达到某个目的，有多种方式（或者造成某种结果，有多种原因），问达到目的的概率是多少（造成这种结果的概率是多少）。

四、贝叶斯公式：

贝叶斯公式，是指当分析样本大到接近总体数时，样本中事件发生的概率将接近于总体中事件发生的概率。

贝叶斯公式：

贝叶斯理论的思路是，**在主观判断的基础上，先估计一个值（先验概率），然后根据观察的新信息不断修正(可能性函数)**。

P(A)：没有数据B的支持下，A发生的概率，也叫做先验概率。这完全是根据经验做出的判断，这也是前面说的贝叶斯公式的主观因素部分。

P(A|B)：在数据B的支持下，A发生的概率，也叫后验概率。即在B事件发生之后，我们对A事件概率的重新评估。

P(B|A)：给定某参数A的概率分布：也叫似然函数。这是一个调整因子，即新信息B带来的调整，作用是使得先验概率更接近真实概率。至于新信息带来的调整作用大不大，还得看因子的值大不大。

该公式又或者：

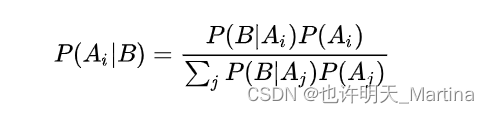
贝叶斯公式就是当已知结果，问导致这个结果的第 i 原因的可能性是多少。

在贝叶斯法则中，每个名词都有约定俗成的名称：

Pr(A)是A的先验概率或边缘概率。之所以称为"先验"是因为它不考虑任何B方面的因素。

Pr(A|B)是已知B发生后A的条件概率，也由于得自B的取值而被称作A的后验概率。

Pr(B|A)是已知A发生后B的条件概率，也由于得自A的取值而被称作B的后验概率。

Pr(B)是B的先验概率或边缘概率，也作标准化常量（normalized constant）。

按这些术语，Bayes法则可表述为：

后验概率 = (似然度 * 先验概率)/标准化常量，也就是说，后验概率与先验概率和似然度的乘积成正比。

另外，比例Pr(B|A)/Pr(B)也有时被称作标准似然度（standardised likelihood），Bayes法则可表述为：后验概率 = 标准似然度 * 先验概率。

最大似然估计：

P(原因1|结果)

P(原因2|结果)

P(原因3|结果)

...

然后这个计算机大脑发现，P(原因i|结果)是最大的，因此就认为呢，造成此种结果的最大原因是原因i。这个就叫最大似然估计（Maximum likelihood estimation，MLE） 。

这种计算算的就是后验概率，后验概率起了这样一个用途，根据一些发生的事实（通常是坏的结果），分析结果产生的最可能的原因，然后才能有针对性地去解决问题。

参考：

简书-贝叶斯公式的理解

先验概率与后验概率 - 知乎