本文探讨了Python脚本与动态模态分解(DMD)的结合应用。我们将利用Python对从OpenFOAM模拟中提取的二维切片数据进行DMD计算。这种方法能够有效地提取隐藏的流动模式,深化对流体动力学现象的理解。

使用开源CFD软件OpenFOAM,有两种方法可以对CFD数据进行DMD计算。第一种方法是直接将OpenFOAM的场数据读入Python;第二种方法则是从OpenFOAM中提取二维切片,然后对这些数据进行DMD计算。
本文将重点介绍第二种方法,即利用Python的强大库直接分析从OpenFOAM提取的二维切片数据,执行DMD并可视化提取的模态。
OpenFOAM案例模态分解准备指南
本研究的起点是雷诺数为100的方形圆柱周围完全发展的、统计稳定的流动。在此基础上,我们将模拟时间延长至100个涡脱落周期。在每个脱落周期内,我们从数据中提取16次二维切片。二维切片的提取是通过OpenFOAM中的
surfaces
函数对象实现的,具体配置如下:
surfaces
{
type surfaces;
libs ("libsampling.so");
writeControl timeStep;
writeInterval 142;
surfaceFormat vtk;
fields (p U);
interpolationScheme cellPoint;
surfaces
{
zNormal
{
type cuttingPlane;
point (0 0 0.05);
normal (0 0 1);
interpolate true;
}
};
};
// ************************************************************************* //
模拟完成后,在案例的
postProcessing
目录中会生成一个名为
surfaces
的子目录,其中包含所有提取的表面数据。目录结构如下:
surfaces/
├── 4771.2000000577236
│ └── zNormal.vtp
├── 4772.6200000577546
│ └── zNormal.vtp
├── 4774.0400000577856
│ └── zNormal.vtp
├── 4775.4600000578166
│ └── zNormal.vtp
.
.
.
在进行后续分析之前,请确保案例模拟已完成且表面数据已成功提取。
表面数据提取
为了从OpenFOAM生成的VTK文件中提取数据,我们将使用PyVista库。PyVista是可视化工具包(VTK)的Python接口,通过NumPy包装VTK库,提供了直接访问数组的方法和类。它为VTK的强大可视化后端提供了一个文档完善的Pythonic接口,便于快速原型设计、分析和空间参考数据集的可视化集成。
PyVista在科学计算可视化中具有重要价值,尤其适用于演示和研究论文的图形生成。同时它也作为其他依赖3D网格渲染的Python模块的支持库。
导入必要的模块,包括PyVista:
importmatplotlib.colors
importmatplotlib.pyplotasplt
importnumpyasnp
importpandasaspd
importfluidfoamasfl
importscipyassp
importos
importmatplotlib.animationasanimation
importpyvistaaspv
importimageio
importio
%matplotlibinline
plt.rcParams.update({'font.size' : 18, 'font.family' : 'Times New Roman', "text.usetex": True})
接下来设置路径变量和常量:
### 常量
d=0.1
Ub=0.015
### 路径
Path='E:/deephub/Sq_Cyl_Surfaces/surfaces/'
save_path='E:/deephub/SquareCylinderData/'
Files=os.listdir(Path)
现在可以尝试读取第一个快照表面:
Data=pv.read(Path+Files[0] +'/zNormal.vtp')
grid=Data.points
x=grid[:,0]
y=grid[:,1]
z=grid[:,2]
rows, columns=np.shape(grid)
print('rows = ', rows, 'columns = ', columns)
print(Data.array_names)
输出:
['TimeValue', 'p', 'U']
从输出可以看出,我们的二维切片包含了时间值、压力场和速度场。利用PyVista,可以为每个快照提取涡量场,并将结果数据组织成一个大型矩阵,以便进行后续的POD计算。具体实现如下:
Data=pv.read(Path+Files[0] +'/zNormal.vtp')
grid=Data.points
x=grid[:,0]
y=grid[:,1]
z=grid[:,2]
rows, columns=np.shape(grid)
print('rows = ', rows, 'columns = ', columns)
### 对U场进行处理
Snaps=len(Files) # 快照数量
data_Vort=np.zeros((rows,Snaps-1))
foriinnp.arange(0,Snaps-1):
data=pv.read(Path+Files[i] +'/zNormal.vtp')
gradData=data.compute_derivative('U', vorticity=True)
grad_pyvis=gradData.point_data['vorticity']
data_Vort[:,i:i+1] =np.reshape(grad_pyvis[:,2], (rows,1), order='F')
np.save(save_path+'VortZ.npy', data_Vort)
让我们检查一下生成的
data_Vort
数组的维度:
data_Vort.shape
### 输出
### (96624, 1600)
此外,我们可以可视化涡量场的一个快照:
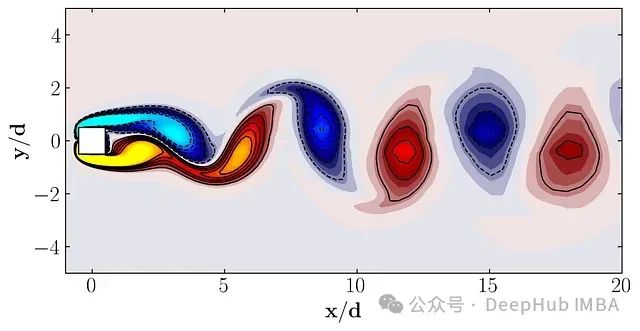
这个可视化结果展示了方形圆柱周围的涡量分布,为我们提供了流场结构的直观认识。
正交分解(POD)
为了确定动态模态分解(DMD)的最佳近似秩,我们可以对涡量场数据进行正交分解(POD)分析。POD是一种强大的降维技术,能够捕捉流场中的主要能量结构。
以下是POD分析的Python实现:
### POD分析
# 构建数据矩阵
X=data_Vort
# 计算并去除平均场
X_mean=np.mean(X, axis=1)
Y=X-X_mean[:,np.newaxis]
# 计算协方差矩阵
C=np.dot(Y.T, Y)/(Y.shape[1]-1)
# 对协方差矩阵进行奇异值分解
U, S, V=np.linalg.svd(C)
# 计算POD模态
Phi_POD=np.dot(Y, U)
# 计算时间系数
a=np.dot(Phi_POD.T, Y)
接下来可以分析POD特征值以评估各模态的能量贡献:
Energy=np.zeros((len(S),1))
foriinnp.arange(0,len(S)):
Energy[i] =S[i]/np.sum(S)
X_Axis=np.arange(Energy.shape[0])
heights=Energy[:,0]
fig, axes=plt.subplots(1, 2, figsize= (12,4))
ax=axes[0]
ax.plot(Energy, marker='o', markerfacecolor='none', markeredgecolor='k', ls='-', color='k')
ax.set_xlim(0, 20)
ax.set_xlabel('Modes')
ax.set_ylabel('Energy Content')
ax=axes[1]
cumulative=np.cumsum(S)/np.sum(S)
ax.plot(cumulative, marker='o', markerfacecolor='none', markeredgecolor='k', ls='-', color='k')
ax.set_xlabel('Modes')
ax.set_ylabel('Cumulative Energy')
ax.set_xlim(0, 20)
plt.show()
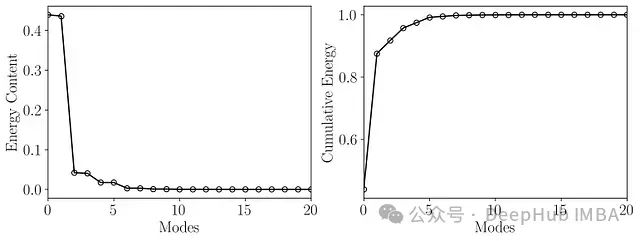
分析结果显示,前21个POD模态捕捉了约99.9%的总能量。这一发现为我们后面选择DMD的近似秩提供了重要依据,表明使用21阶近似进行DMD分析是合理的。
以下是前几个POD模态的可视化结果,用于参考:
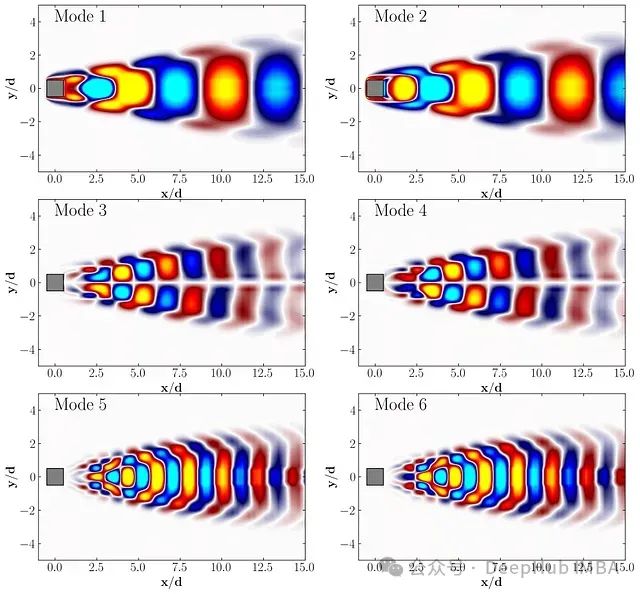
这些模态图展示了流场中的主要结构,为我们理解流动特性提供了直观的洞察。
动态模态分解(DMD)
动态模态分解是一种强大的技术,能够提取流场中的动态特征。以下是DMD算法的Python实现:
defDMD(X1, X2, r, dt):
# 对X1进行奇异值分解
U, s, Vh=np.linalg.svd(X1, full_matrices=False)
# 截断SVD矩阵
Ur=U[:, :r]
Sr=np.diag(s[:r])
Vr=Vh.conj().T[:, :r]
# 构建Atilde矩阵并计算其特征值和特征向量
Atilde=Ur.conj().T@X2@[email protected](Sr)
Lambda, W=np.linalg.eig(Atilde)
# 计算DMD模态
Phi=X2@[email protected](Sr) @W
# 计算连续时间特征值
omega=np.log(Lambda)/dt
# 计算DMD模态振幅
alpha1=np.linalg.lstsq(Phi, X1[:, 0], rcond=None)[0]
b=np.linalg.lstsq(Phi, X2[:, 0], rcond=None)[0]
# DMD重构
time_dynamics=None
foriinrange(X1.shape[1]):
v=np.array(alpha1)[:,0]*np.exp( np.array(omega)*(i+1)*dt)
iftime_dynamicsisNone:
time_dynamics=v
else:
time_dynamics=np.vstack((time_dynamics, v))
X_dmd=np.dot(np.array(Phi), time_dynamics.T)
returnPhi, omega, Lambda, alpha1, b, X_dmd
为了应用这个DMD函数,我们首先需要准备时间偏移的数据矩阵:
# 获取数据矩阵的两个时间步长偏移视图
X1=np.matrix(X[:, 0:-1])
X2=np.matrix(X[:, 1:])
然后,我们定义近似秩和时间步长:
r=21 # 根据POD分析结果选择
dt=0.01*142
接下来,我们执行DMD计算:
Phi, omega, Lambda, alpha1, b, X_dmd=DMD(X1, X2, r, dt)
在进行可视化之前,我们首先分析DMD特征值的分布。这有助于我们理解所识别的DMD模态的动态特性。我们将实部和虚部特征值绘制在单位圆上:
theta=np.linspace(0, 2*np.pi, 150)
radius=1
a=radius*np.cos(theta)
b=radius*np.sin(theta)
fig, ax=plt.subplots()
ax.scatter(np.real(Lambda), np.imag(Lambda), color='r', marker='o', s=100)
ax.plot(a, b, color='k', ls='--')
ax.set_xlabel(r'$\Lambda_r$')
ax.set_ylabel(r'$\Lambda_i$')
ax.set_aspect('equal')
plt.show()
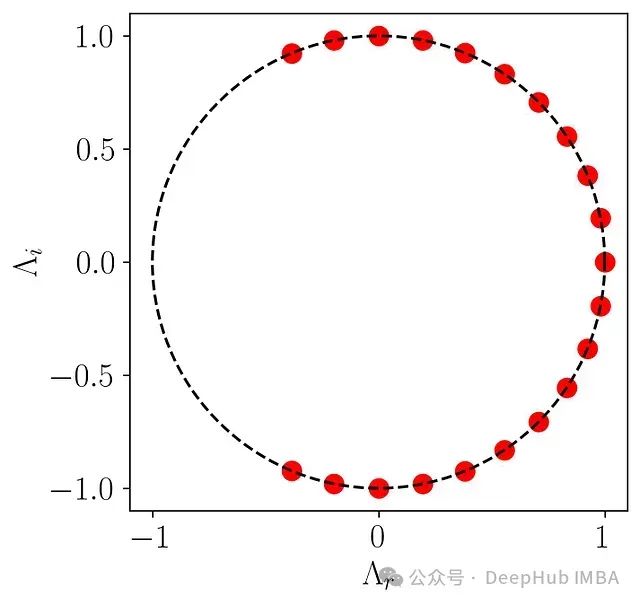
这个图显示所有特征值都位于单位圆上,表明DMD模态既不增长也不衰减,呈现稳定的特性。
为了可视化DMD模态,我们首先需要将DMD模态矩阵转换为数组:
A=np.squeeze(np.asarray(Phi))
然后可以使用Matplotlib绘制DMD模态:
Rect1=plt.Rectangle((-0.5, -0.5), 1, 1, ec='k', color='white', zorder=2)
Mode=11
fig, ax=plt.subplots(figsize=(11, 4))
p=ax.tricontourf(x/0.1, y/0.1, np.real(A[:,Mode]), levels=1001, vmin=-0.005, vmax=0.005, cmap=cmap)
ax.add_patch(Rect1)
ax.xaxis.set_tick_params(direction='in', which='both')
ax.yaxis.set_tick_params(direction='in', which='both')
ax.xaxis.set_ticks_position('both')
ax.yaxis.set_ticks_position('both')
ax.set_xlim(-1, 20)
ax.set_ylim(-5, 5)
ax.set_aspect('equal')
ax.set_xlabel(r'$\bf x/d$')
ax.set_ylabel(r'$\bf y/d$')
ax.text(0, 4, r'$f_i ='+str(np.imag(Lambda[Mode])) +'$', fontsize=25, color='black')
plt.show()
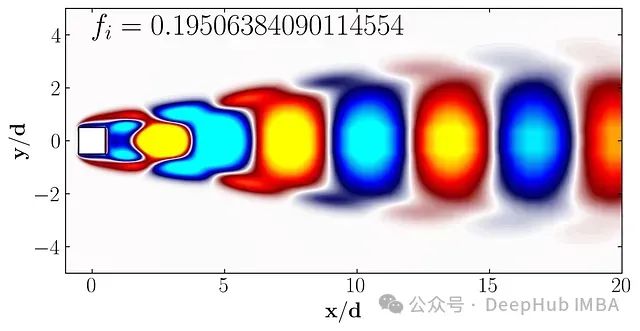
这个图展示了第11个DMD模态的空间结构。类似地,我们可以绘制前6个DMD模态:

这些DMD模态图揭示了流场中的关键动态结构,为我们深入理解方形圆柱周围的流动特性提供了重要依据。
通过结合POD和DMD分析,我们不仅捕捉了流场的主要能量结构,还揭示了这些结构随时间的演化特性。这种综合分析方法为复杂流动系统的研究提供了强大的工具,能够帮助我们更深入地理解流体动力学现象。
总结
本文详细介绍了一种基于OpenFOAM和Python的流场动态分析方法。我们从OpenFOAM模拟数据的提取和处理开始,利用PyVista库高效地处理二维切片数据。通过正交分解(POD)成功捕捉了流场的主要能量结构,为动态模态分解(DMD)的应用奠定了基础。DMD分析进一步揭示了流场的动态特征,使我们能够深入理解方形圆柱周围的复杂流动现象。
这种结合OpenFOAM、POD和DMD的综合分析方法,不仅提高了对复杂流体系统的认识,还为流体动力学研究提供了强大的工具。Python的灵活性和效率在整个分析过程中发挥了关键作用,展示了其在科学计算和数据可视化方面的优势。
作者:Shubham Goswami