机器学习:过拟合与欠拟合是如何被解决的?
什么是过拟合与欠拟合
机器学习的主要挑战是我们的算法能够在为观测的数据上误差较小,而不是在只在训练集上表现良好,我们这种能力我们称之为泛化。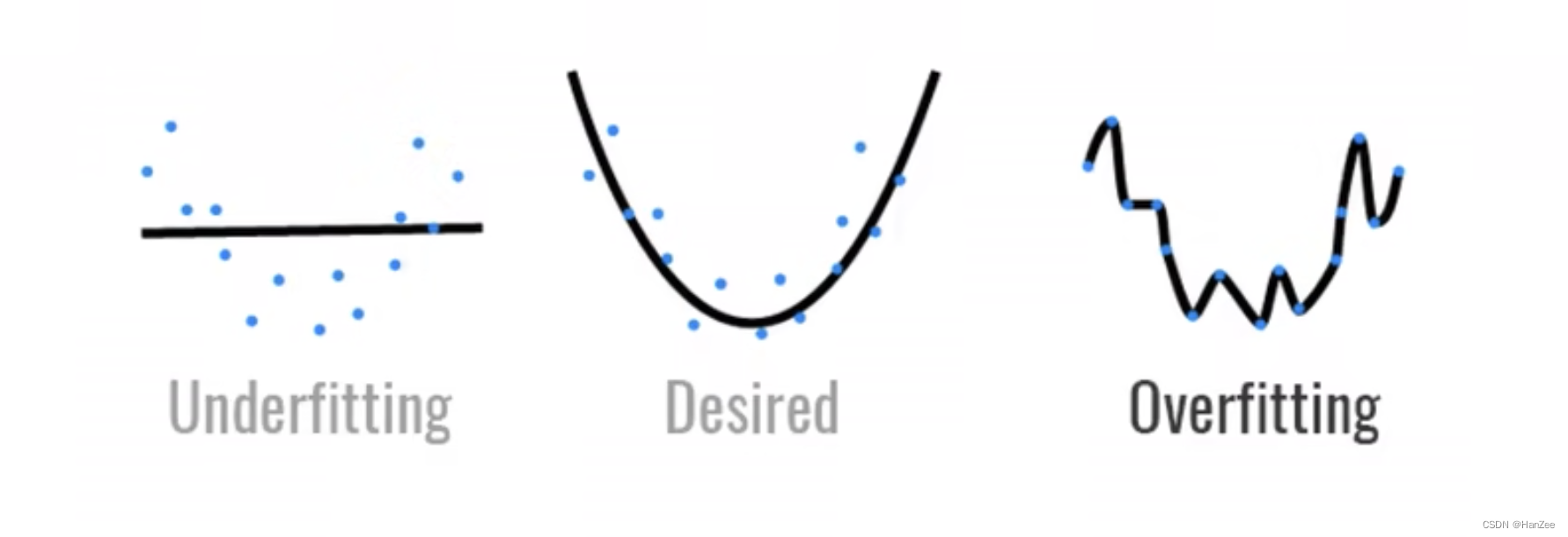
过拟合
如上右图所示,模型通过训练集很好的拟合了观测数据,训练误差很小,但是由于过度的在训练集上拟合,当其用于推理测试数据时,误差很可能会变大,因为数据是有噪声的并且其本身与真实概率分布也有一定偏差,训练集的概率分布与真实概率分布还是有一定差距的,当模型过度的接近训练集的概率分布,那么他就会随着训练轮数的增加而远离真实的概率分布(这里我们假设测试集复合真实概率分布),以上的情况我们称之为过拟合。
欠拟合
如上左图所示,模型通过训练集拟合的直线不能很好的拟合图中的观测值,训练误差和泛化误差都非常高,我们称之为欠拟合。
如何解决过拟合
L2正则化(权重衰减)
谈到正则化,我们继续观察上面过拟合图像,函数过度的复杂了(太弯弯绕了~),我们首先想到的一定是降低他的复杂度,也就是说我们要减少权重参数的维度与大小(权重衰减),它的维度决定了图像他有个拐点,大小则决定了图像弯曲程度。那么我们就有了一个想法了💡!
我们从权重衰减的方向入手(也就是参数的大小):
我们让权重参数的二范数小于某个值来约束它。在优化损失函数(以MSE为例)的时候可得如下方程组:
{
min
1
n
∑
i
=
1
n
(
w
i
x
i
−
y
i
)
2
∥
w
∥
2
2
<
=
σ
\begin{cases}\min \dfrac{1}{n}\sum ^{n}_{i=1}\left( w_{i}x_{i}-y_{i}\right) ^{2}\\ \left\| w\right\| _{2}^{2}<= \sigma\end{cases}
⎩⎨⎧minn1∑i=1n(wixi−yi)2∥w∥22<=σ
这里我们根据拉格朗日乘子法 ,可以把在约束内求最值,改成无范围求最值。得到下方方程(lambda为惩罚系数):
L
(
w
)
=
1
n
∑
i
=
1
n
(
w
i
x
i
−
y
i
)
+
1
2
λ
∑
i
=
1
n
(
w
i
)
2
L\left( w\right) =\dfrac{1}{n}\sum ^{n}_{i=1}\left( w_{i}x_{i}-y_{i}\right) + \dfrac{1}{2} \lambda\sum ^{n}_{i=1}\left( w_{i}\right) ^{2}
L(w)=n1i=1∑n(wixi−yi)+21λi=1∑n(wi)2
根据梯度下降法(
α
\alpha
α为learning rate),我们继续化简:
W
n
e
w
=
W
−
α
L
(
w
)
′
=
W
−
α
x
−
λ
α
w
=
(
1
−
α
x
)
w
−
α
x
\begin{aligned}W_{new}=W-\alpha L\left( w\right)^\prime \\ =W-\alpha x-\lambda \alpha w\\ =\left( 1-\alpha x\right) w-\alpha x\end{aligned}
Wnew=W−αL(w)′=W−αx−λαw=(1−αx)w−αx
我们发现,参数w每回合都在慢慢减少,权重系数减少,也就是对数据与噪声变得不敏感(曲线越平滑,根据泰勒展开可知),相对来讲,也就是降低了数据的拟合程度从而缓解过拟合。
这里我们要注意,其中衰减的参数包含偏置系数b,因为权重系数决定了模型推理结果的方差,而偏置系数决定了偏差,不能缓解过拟合。
代码实现
%matplotlib inline
import torch
from torch import nn
from d2l import torch as d2l
n_train, n_test, num_inputs, batch_size =20,100,200,5
true_w, true_b = torch.ones((num_inputs,1))*0.05,0.05
train_data = d2l.synthetic_data(true_w, true_b,n_train)
train_iter = d2l.load_array(train_data, batch_size)
test_data = d2l.synthetic_data(true_w, true_b, n_train)
test_iter = d2l.load_array(test_data,batch_size, is_train=False)definit_params():
w = torch.normal(0,1,size=(num_inputs,1),requires_grad =True)
b = torch.zeros(1,requires_grad =True)return[w,b]defl2_penalty(w):return torch.sum(torch.abs(w))
num_epochs, lr =1000,0.003deftrain(lambd):
w,b = init_params()
net,loss =lambda X : d2l.linreg(X,w,b), d2l.squared_loss
animator = d2l.Animator(xlabel='epochs', ylabel='loss', yscale='log',
xlim=[5, num_epochs], legend=['train','test'])for epoch inrange(num_epochs):for X,y in train_iter:
l = loss(net(X),y)+lambd*l2_penalty(w)
l.sum().backward()
d2l.sgd([w,b],lr,batch_size)if(epoch +1)%5==0:
animator.add(epoch +1,(d2l.evaluate_loss(net, train_iter, loss),
d2l.evaluate_loss(net, test_iter, loss)))print('w的L2范数是:', torch.norm(w).item())
train(lambd=1)
降维
剔除掉冗余的特征和比重不大的特征,原因。
2. 采用合适的模型(控制模型的复杂度)
采用合适的模型
过于复杂的模型会带来过拟合问题。对于模型的设计,目前公认的一个深度学习规律"deeper is better"。国内外各种大牛通过实验和竞赛发现,对于CNN来说,层数越多效果越好,但是也更容易产生过拟合,并且计算所耗费的时间也越长。
根据奥卡姆剃刀法则:在同样能够解释已知观测现象的假设中,我们应该挑选“最简单”的那一个。对于模型的设计而言,我们应该选择简单、合适的模型解决复杂的问题。
数据增强
如何解决欠拟合
欠拟合的问题一般出现在训练开始,随着训练的深入,一般此问题会不攻自破,我们一般采用:
- 增加模型的复杂度(比如从直线->曲线)。
- 增加数据维度(维度数应该远远小于数据的数量,否则可能出现过拟合)。
- 增加数据量。
版权归原作者 HanZee 所有, 如有侵权,请联系我们删除。