视觉SLAM总结——SuperPoint / SuperGlue
视觉SLAM总结——SuperPoint / SuperGlue
在我刚开始接触SLAM算法的时候听到过一个大佬讲:“SLAM其实最重要的是前端,如果特征匹配做得足够鲁棒,后端就可以变得非常简单”,当时自己总结过一篇传统视觉特征的博客视觉SLAM总结——视觉特征子综述,由于当时对深度学习了解不够,因此并没有涵盖基于深度学习的视觉特征匹配方法,而实际上,基于深度学习的特征匹配效果要远优于传统方法。本博客结合代码对2018年提出的SuperPoint和2020年提出的SuperGlue两篇最为经典的深度学习算法进行学习总结。
1. SuperPoint
SuperPoint发表于2018年,原论文名为《SuperPoint: Self-Supervised Interest Point Detection and Description
》,该方法使用无监督的方式训练了一个用于提取图像特征以及特征描述子的网络。
1.1 网络结构
SuperPoint的网络结构如下图所示:
我们知道,图像特征通常包括两部分,特征点已经特征描述子,上图中两个分支即分别用来提取特征点和特征描述子。网络首先使用了VGG-Style的Encoder用于降低图像尺寸提取特征,Encoder部分由卷积层、Max-Pooling层和非线性激活层组成,通过三个Max-Pooling层将图像尺寸变为输出的
1
/
8
1/8
1/8,代码如下:
# Shared Encoder
x = self.relu(self.conv1a(data['image']))
x = self.relu(self.conv1b(x))
x = self.pool(x)
x = self.relu(self.conv2a(x))
x = self.relu(self.conv2b(x))
x = self.pool(x)
x = self.relu(self.conv3a(x))
x = self.relu(self.conv3b(x))
x = self.pool(x)
x = self.relu(self.conv4a(x))
x = self.relu(self.conv4b(x))# x的输出维度是(N,128,W/8, H/8)
对于特征点提取部分,网路先将维度
(
W
/
8
,
H
/
8
,
128
)
(W/8, H/8, 128)
(W/8,H/8,128)的特征处理为
(
W
/
8
,
H
/
8
,
65
)
(W/8, H/8, 65)
(W/8,H/8,65)大小,这里的
65
65
65的含义是特征图的每一个像素表示原图
8
×
8
8\times8
8×8的局部区域加上一个当局部区域不存在特征点时用于输出的Dustbin通道,通过Softmax以及Reshape的操作,最终特征会恢复为原图大小,代码如下:
# Compute the dense keypoint scores
cPa = self.relu(self.convPa(x))# x维度是(N,128,W/8, H/8)
scores = self.convPb(cPa)# scores维度是(N,65,W/8, H/8)
scores = torch.nn.functional.softmax(scores,1)[:,:-1]# scores维度是(N,64,W/8, H/8)
b, _, h, w = scores.shape
scores = scores.permute(0,2,3,1).reshape(b, h, w,8,8)# scores维度是(N,W/8, H/8, 8, 8)
scores = scores.permute(0,1,3,2,4).reshape(b, h*8, w*8)# scores维度是(N,W/8, H/8)
scores = simple_nms(scores, self.config['nms_radius'])
这里指的注意的是我们是先对包括Dustbin通道的特征图进行Softmax操作后再进行Slice的。假如没有Dustbin通道,当
8
×
8
8\times8
8×8的局部区域内没有特征点时,经过Softmax后64维的特征势必还是会有一个相对较大的值输出,但加入Dustbin通道后就可以避免这个问题,因此需要在Softmax操作后再进行Slice。最后再经过NMS后相应较大的位置即为输出的特征点。
对于特征描述子提取部分,网络先将维度
(
W
/
8
,
H
/
8
,
128
)
(W/8, H/8, 128)
(W/8,H/8,128)的特征处理为
(
W
/
8
,
H
/
8
,
256
)
(W/8, H/8, 256)
(W/8,H/8,256)大小,其中
256
256
256将是我们即将输出的特征的维度。按照通道进行归一化后根据特征点的位置通过双线性插值得到特征向量。
# Compute the dense descriptors
cDa = self.relu(self.convDa(x))
descriptors = self.convDb(cDa)# descriptor的维度是(N,256,8,8)
descriptors = torch.nn.functional.normalize(descriptors, p=2, dim=1)# 按通道进行归一化# Extract descriptors
descriptors =[sample_descriptors(k[None], d[None],8)[0]for k, d inzip(keypoints, descriptors)]
其中双线性插值相关的操作在sample_descriptors中,该函数如下:
defsample_descriptors(keypoints, descriptors, s:int=8):""" Interpolate descriptors at keypoint locations """
b, c, h, w = descriptors.shape
keypoints = keypoints - s /2+0.5
keypoints /= torch.tensor([(w*s - s/2-0.5),(h*s - s/2-0.5)],).to(keypoints)[None]# 这里*s的原因是keypoints在(W,H)特征图上提取的,而descriptor目前是在(W/s,H/s)的特征图上提取的
keypoints = keypoints*2-1# normalize to (-1, 1)
args ={'align_corners':True}if torch.__version__ >='1.3'else{}
descriptors = torch.nn.functional.grid_sample(
descriptors, keypoints.view(b,1,-1,2), mode='bilinear',**args)# 双线性插值
descriptors = torch.nn.functional.normalize(
descriptors.reshape(b, c,-1), p=2, dim=1)return descriptors
以上就完成了SuperPoint前向部分特征点和特征向量的提取过程,接下来看下这个网络是如何训练的?
1.2 损失函数
首先我们看下基于特征点和特征向量是如何建立损失函数的,损失函数公式如下:
L
(
X
,
X
′
,
D
,
D
′
;
Y
,
Y
′
,
S
)
=
L
p
(
X
,
Y
)
+
L
p
(
X
′
,
Y
′
)
+
λ
L
d
(
D
,
D
′
,
S
)
\mathcal{L}\left(\mathcal{X}, \mathcal{X}^{\prime}, \mathcal{D}, \mathcal{D}^{\prime} ; Y, Y^{\prime}, S\right)=\mathcal{L}_{p}(\mathcal{X}, Y)+\mathcal{L}_{p}\left(\mathcal{X}^{\prime}, Y^{\prime}\right)+\lambda \mathcal{L}_{d}\left(\mathcal{D}, \mathcal{D}^{\prime}, S\right)
L(X,X′,D,D′;Y,Y′,S)=Lp(X,Y)+Lp(X′,Y′)+λLd(D,D′,S)其中
L
p
\mathcal{L}_{p}
Lp为特征点相关的损失,
L
d
\mathcal{L}_{d}
Ld为特征向量相关的损失,其中
X
\mathcal{X}
X、
Y
Y
Y、
D
\mathcal{D}
D分别为图像上通过网络提取的特征点、特征向量和特征点的真值。
特征点相关损失
L
p
\mathcal{L}_{p}
Lp定义为一个交叉熵损失:
L
p
(
X
,
Y
)
=
1
H
c
W
c
∑
h
=
1
w
=
1
H
c
,
W
c
l
p
(
x
h
w
;
y
h
w
)
\mathcal{L}_{p}(\mathcal{X}, Y)=\frac{1}{H_{c} W_{c}} \sum_{{h=1 \\ w=1}}^{H_{c}, W_{c}} l_{p}\left(\mathbf{x}_{h w} ; y_{h w}\right)
Lp(X,Y)=HcWc1h=1w=1∑Hc,Wclp(xhw;yhw)其中
l
p
(
x
h
w
;
y
h
w
)
=
−
log
(
exp
(
x
h
w
y
)
∑
k
=
1
65
exp
(
x
h
w
k
)
)
l_{p}\left(\mathbf{x}_{h w} ; y_{h w}\right)=-\log \left(\frac{\exp \left(\mathbf{x}_{h w y}\right)}{\sum_{k=1}^{65} \exp \left(\mathbf{x}_{h w k}\right)}\right)
lp(xhw;yhw)=−log(∑k=165exp(xhwk)exp(xhwy))其中
H
c
=
H
/
8
H_{c}=H/8
Hc=H/8,
W
c
=
W
/
8
W_{c}=W/8
Wc=W/8;
y
h
w
y_{h w}
yhw为真值,即
8
×
8
8\times8
8×8的方格中哪个Pixel为特征点;
x
h
w
\mathbf{x}_{h w}
xhw是一个长度为
65
65
65的特征向量,向量的每一个数值代表相应的Pixel上特征点的响应值。
特征向量相关损失
L
d
\mathcal{L}_{d}
Ld定义为一个合页损失(Hinge-Loss,在SVM算法中用到):
L
d
(
D
,
D
′
,
S
)
=
1
(
H
c
W
c
)
2
∑
h
=
1
w
=
1
H
c
,
W
c
∑
h
′
=
1
w
′
=
1
H
c
,
W
c
l
d
(
d
h
w
,
d
h
′
w
′
′
;
s
h
w
h
′
w
′
)
\mathcal{L}_{d}\left(\mathcal{D}, \mathcal{D}^{\prime}, S\right)=\frac{1}{\left(H_{c} W_{c}\right)^{2}} \sum_{{h=1 \\ w=1}}^{H_{c}, W_{c}} \sum_{{h^{\prime}=1 \\ w^{\prime}=1}}^{H_{c}, W_{c}} l_{d}\left(\mathbf{d}_{h w}, \mathbf{d}_{h^{\prime} w^{\prime}}^{\prime} ; s_{h w h^{\prime} w^{\prime}}\right)
Ld(D,D′,S)=(HcWc)21h=1w=1∑Hc,Wch′=1w′=1∑Hc,Wcld(dhw,dh′w′′;shwh′w′)其中
l
d
(
d
,
d
′
;
s
)
=
λ
d
∗
s
∗
max
(
0
,
m
p
−
d
T
d
′
)
+
(
1
−
s
)
∗
max
(
0
,
d
T
d
′
−
m
n
)
l_{d}\left(\mathbf{d}, \mathbf{d}^{\prime} ; s\right)=\lambda_{d} * s * \max \left(0, m_{p}-\mathbf{d}^{T} \mathbf{d}^{\prime}\right)+(1-s) * \max \left(0, \mathbf{d}^{T} \mathbf{d}^{\prime}-m_{n}\right)
ld(d,d′;s)=λd∗s∗max(0,mp−dTd′)+(1−s)∗max(0,dTd′−mn)其中
λ
d
\lambda_{d}
λd为定义的权重,
s
h
w
h
′
w
′
s_{h w h^{\prime} w^{\prime}}
shwh′w′为判断是通过单应矩阵关联判断否为同一个特征点的函数:
s
h
w
h
′
w
′
=
{
1
,
if
∥
H
p
h
w
^
−
p
h
′
w
′
∥
≤
8
0
,
otherwise
s_{h w h^{\prime} w^{\prime}}= \begin{cases}1, & \text { if }\left\|\widehat{\mathcal{H} \mathbf{p}_{h w}}-\mathbf{p}_{h^{\prime} w^{\prime}}\right\| \leq 8 \\ 0, & \text { otherwise }\end{cases}
shwh′w′={1,0, if ∥∥∥Hphw−ph′w′∥∥∥≤8 otherwise 其中
p
\mathbf{p}
p为
8
×
8
8\times8
8×8的方格的中心点,当
H
p
h
w
^
\widehat{\mathcal{H} \mathbf{p}_{h w}}
Hphw和
p
h
′
w
′
\mathbf{p}_{h^{\prime} w^{\prime}}
ph′w′距离小于8个像素时认为匹配成功,一个放个对应的其实是一个特征点。此外我们来分析下合页损失,当匹配成功时,当相似度
d
T
d
′
\mathbf{d}^{T} \mathbf{d}^{\prime}
dTd′大于正样本阈值
m
p
m_{p}
mp时会进行惩罚;当匹配失败时,当相似度
d
T
d
′
\mathbf{d}^{T} \mathbf{d}^{\prime}
dTd′小于负样本阈值
m
p
m_{p}
mp时会进行惩罚。在这样的损失函数作用下,**当匹配成功时,相似度就应该很大,匹配失败时,相似度就应该很小**。
1.3 自监督训练过程
以上就是网路损失函数的相关定义,在SuperPoint论文中很重要的一部分就是不监督训练,下面我们来看看该网络是如何实无监督训练的。网络训练一共分为如下几部分: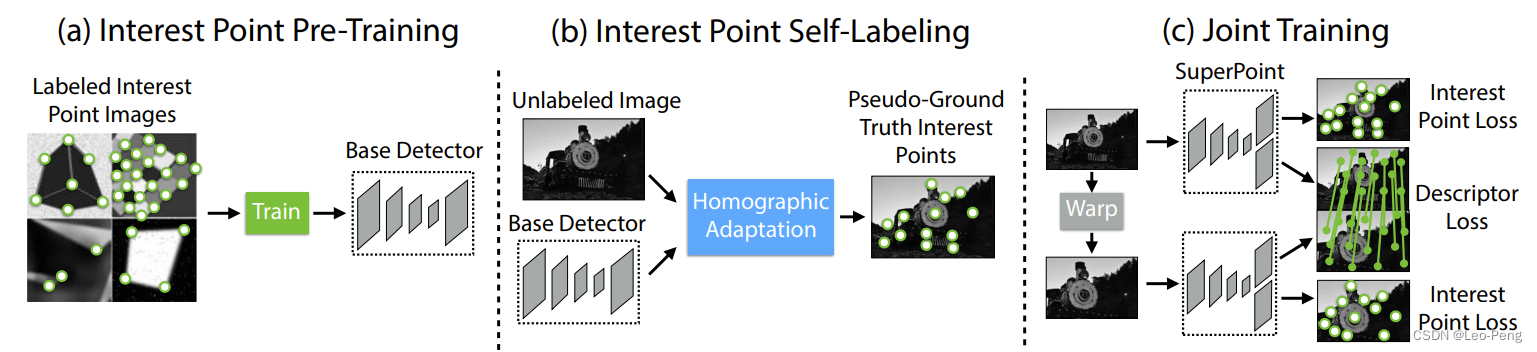
第一步是在如下图所示的Synthetic Shapes Dataset上进行预训练,训练的结果成为MagicPoint。虽然是在合成的数据集上进行训练的,但是论文中提到MagicPoint在Corner-Like Structure的现实场景也具备一定的泛化能力,而面对更加普遍的场景,MagicPoint的效果就会下降,为此作者增加了第二步,即Homographic Adaption。
第二步的Homographic Adaption的流程如下图所示:
我们假设
f
θ
(
⋅
)
f_{\theta}(\cdot)
fθ(⋅)为MagicPoint的检测模型,
I
I
I为输入图像,
X
\mathbf{X}
X为MagicPoint检测的特征点,
H
\mathcal{H}
H为随机的单应矩阵。首先我们有:
x
=
f
θ
(
I
)
\mathbf{x}=f_{\theta}(I)
x=fθ(I)我们对图像进行单应变换,如果特征点检测算法具备单应不变性(这也是我们希望具备的),那么就应该满足如下公式:
H
x
=
f
θ
(
H
(
I
)
)
\mathcal{H} \mathbf{x}=f_{\theta}(\mathcal{H}(I))
Hx=fθ(H(I))对公式进行变换:
x
=
H
−
1
f
θ
(
H
(
I
)
)
\mathbf{x}=\mathcal{H}^{-1} f_{\theta}(\mathcal{H}(I))
x=H−1fθ(H(I))然后哦我们采样尽可能多的随机单应矩阵就可以得到足够多的具备单应不变性的特征点的真值:
F
^
(
I
;
f
θ
)
=
1
N
h
∑
i
=
1
N
h
H
i
−
1
f
θ
(
H
i
(
I
)
)
\hat{F}\left(I ; f_{\theta}\right)=\frac{1}{N_{h}} \sum_{i=1}^{N_{h}} \mathcal{H}_{i}^{-1} f_{\theta}\left(\mathcal{H}_{i}(I)\right)
F^(I;fθ)=Nh1i=1∑NhHi−1fθ(Hi(I))
第三步则是根据前面提供的损失函数进行迭代训练。
以上就完成SuperPoint算法的基本原理介绍,其效果如下: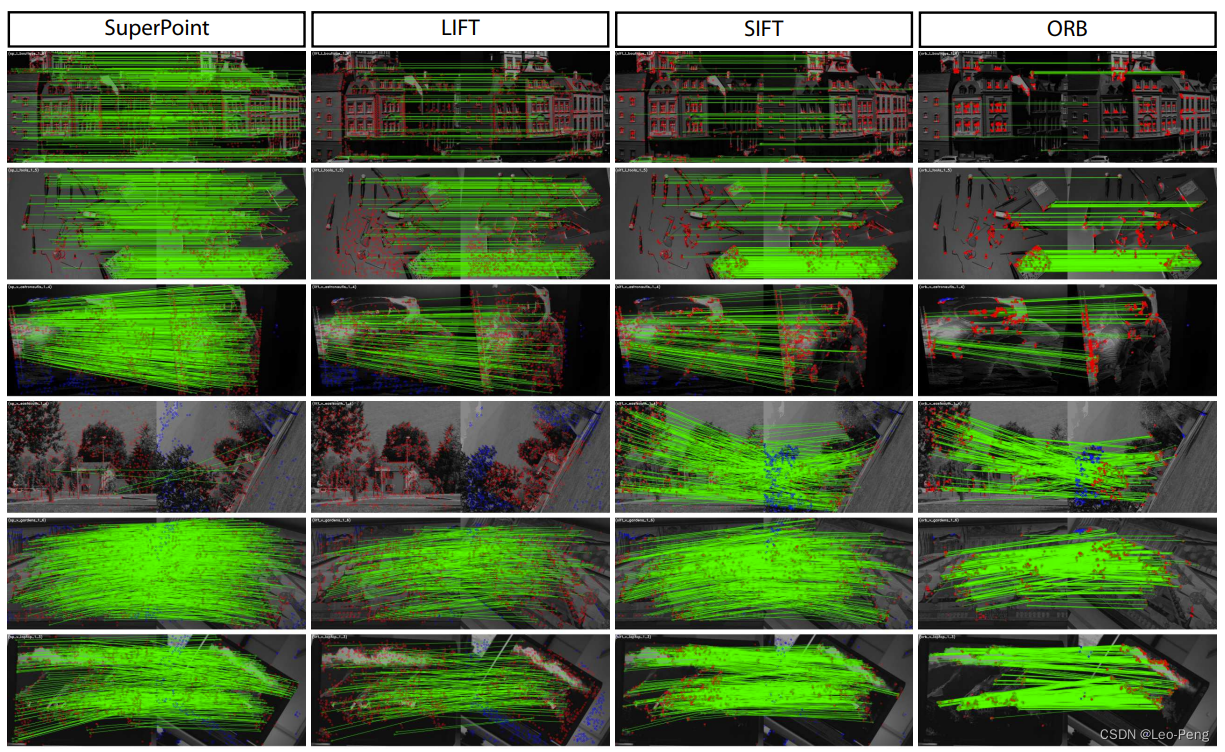
我们可以看到第四行SuperPoint的表现其实很差,我们知道单应变化成立的前提条件是场景中存在平面,而第四行的场景很显然不太满足这种条件,因此效果也会比较差,这也体现了SuperPoint在自监督训练下的一些不足之处。
2. SuperGlue
SupreGlue发表于2020年,原论文名为《SuperGlue: Learning Feature Matching with Graph Neural Networks》,该论文引入了Transformer实现了一种2D特征点匹配方法。我们知道,在经典的SLAM框架中,前端进行特征提取,后端进行非线性优化,而中间非常重要的一步就是特征匹配,传统的特征匹配通常是结合最近邻、RASANC等一些算法进行处理,SuperGlue的推出是SLAM算法迈向端到端深度学习的一个重要里程碑。由于下面的网络介绍中涉及到Transformer的相关知识,对这部分知识不熟悉的同学可以参考下计算机视觉算法——Transformer学习笔记。
2.1 Sinkhorn算法
SuperGlue论文中给出的算法Pipeline如下图所示: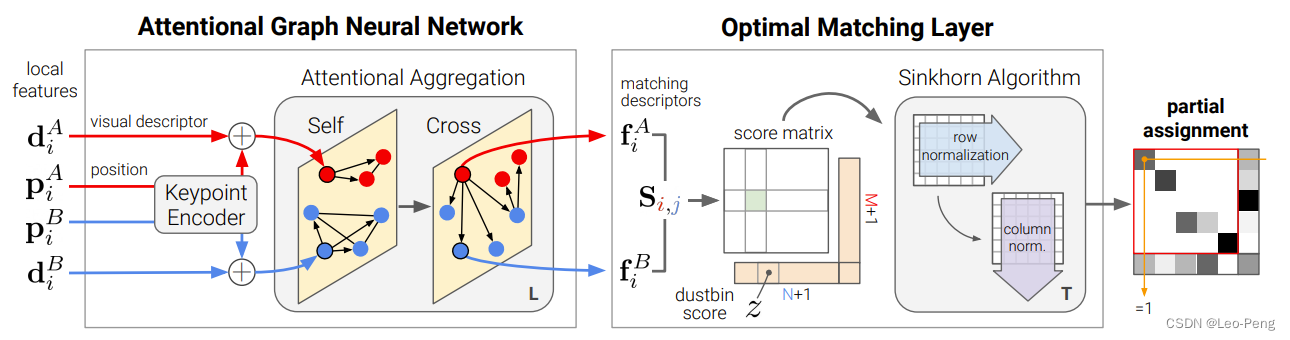
从算法Pipeline可以看出,算法通过Attentional Graph Neural Network输出一个Score Matrix,在Optimal Matching Layer中使用Sinkhorn Algorithm得到最终的匹配结果,这里我们先来搞清楚这个Score Matrix是什么,后文再讨论如何得到这个Score Matrix,要搞清楚Score Matrix的含义,我们就得先了解Sinkhorn Algorithm的基本原理。
Sinkhorn Algorithm解决的是最有传输问题,即解决如何以最小代价将一个分布转移为另一个分布的问题,这里我们参考博客Notes on Optimal Transport中的一个例子来说明该算法:
家里有的水果种类和份数如下表所示:
水果类别苹果梨子份数21
家庭成员对水果的需求量如下表所示:
家庭成员小A小B小C需求数量111
然后团队成员不同家庭成员对不用水果的喜好程度还不一样,如下表所示:
小A小B小C苹果012梨子201
那么我们怎样分配水果才能使得整体最优呢?如果我们将该问题当作一个二分图问题的话,那么可以使用匈牙利匹配或者KM算法求解,但是二分图问题要求对象是不可微分的,也就是说水果是不可以切开的。但是Sinkhorn Algorithm解决的是可微分问题,也就是这里我们分水果的时候可以将水果切开分。
下面我们通过公式来定义该问题,我们定义家庭成员对水果的需求为
c
=
(
1
,
1
,
1
)
⊤
\mathbf{c}=(1,1,1)^{\top}
c=(1,1,1)⊤,水果的数量分布为
r
=
(
2
,
1
)
⊤
\mathbf{r}=(2,1)^{\top}
r=(2,1)⊤,接下来我们定义分配矩阵
U
(
r
,
c
)
U(\mathbf{r}, \mathbf{c})
U(r,c)为
U
(
r
,
c
)
=
{
P
∈
R
>
0
n
×
m
∣
P
1
m
=
r
,
P
⊤
1
n
=
c
}
U(\mathbf{r}, \mathbf{c})=\left\{P \in \mathbb{R}_{>0}^{n \times m} \mid P \mathbf{1}_{m}=\mathbf{r}, P^{\top} \mathbf{1}_{n}=\mathbf{c}\right\}
U(r,c)={P∈R>0n×m∣P1m=r,P⊤1n=c}
U
(
r
,
c
)
U(\mathbf{r}, \mathbf{c})
U(r,c)包含了所有分配的可能性,接下来我们根据团队成员对甜点的定义损失矩阵
M
M
M,我们最佳的分配方案应该满足
d
M
(
r
,
c
)
=
min
P
∈
U
(
r
,
c
)
∑
i
,
j
P
i
j
M
i
j
d_{M}(\mathbf{r}, \mathbf{c})=\min _{P \in U(\mathbf{r}, \mathbf{c})} \sum_{i, j} P_{i j} M_{i j}
dM(r,c)=P∈U(r,c)mini,j∑PijMij注意这里不是矩阵相乘,而是逐个像素相乘再相加。使用Sinkhorn Algorithm求解该问题的流程其实非常简单,如下图所示:
 首先根据损失矩阵
首先根据损失矩阵
M
M
M定义一个分配矩阵
P
λ
=
e
−
λ
M
P_{\lambda}=e^{-\lambda M}
Pλ=e−λM,然后进行迭代计算,每次迭代先将每一行的值进行归一化后乘以
r
\mathbf{r}
r,也就是使得分配矩阵该行所有的值加起来正好为
r
\mathbf{r}
r,例如该行表示苹果的分配情况,那么
r
=
2
\mathbf{r}=2
r=2。同理,对每列进行归一化后乘以
C
\mathbf{C}
C,如此迭代直到收敛,收敛后的分配矩阵即我们最后的最优分配结果。我写了一个非常简单的测试程序如下:
import numpy as np
cost = np.array([[0,1,2],[2,0,1]], dtype=np.float)
row_weight = np.array([2,1])
col_weight = np.array([1,1,1])for _ inrange(100):
cost = cost / np.sum(cost, axis=1).reshape(2,-1)* row_weight.reshape(2,-1)print(cost)
cost = cost / np.sum(cost, axis=0).reshape(-1,3)* col_weight.reshape(-1,3)print(cost)
最后输出的结果为:
[[0.1.0.99340351][1.0.0.00659649]]
很合理地,算法将苹果分给了更喜欢的小B和小C,而小A得到的是他最爱的梨子,这个算法流程其实非常简单,但是为什么会这样就能得到最优?什么情况下会不收敛?这些问题我暂时没有投入太多时间去深入了解,之后有时间再补上。
2.2 网络结构
下面我们结合代码一步一步解析SuperGlue的网络Pipeline是怎样得到Score矩阵
S
\mathbf{S}
S以及SuperGlue算法针对遮挡、噪声等问题实现的一些Trick:
假定有
A
、
B
A、B
A、B两张图像,分别检测出
M
M
M和
N
N
N个特征点,分别记为
A
:
=
{
1
,
…
,
M
}
\mathcal{A}:=\{1, \ldots, M\}
A:={1,…,M}和
B
:
=
{
1
,
…
,
N
}
\mathcal{B}:=\{1, \ldots, N\}
B:={1,…,N},每个特征点由
(
p
,
d
)
(\mathbf{p}, \mathbf{d})
(p,d)表示,其中
p
i
:
=
(
x
,
y
,
c
)
i
\mathbf{p}_{i}:=(x, y, c)_{i}
pi:=(x,y,c)i为第
i
i
i个特征点的(归一化后的)位置和置信度,
d
i
∈
R
D
\mathbf{d}_{i} \in \mathbb{R}^{D}
di∈RD为第
i
i
i个特征点的特征向量。我们首先对输入网络的特征点和特征向量进行编码:
(
0
)
x
i
=
d
i
+
M
L
P
e
n
c
(
p
i
)
{ }^{(0)} \mathbf{x}_{i}=\mathbf{d}_{i}+\mathbf{M L P}_{\mathrm{enc}}\left(\mathbf{p}_{i}\right)
(0)xi=di+MLPenc(pi)其作用就是特征点的位置和特征向量编码进同一个特征
(
0
)
x
i
{ }^{(0)} \mathbf{x}_{i}
(0)xi,使得网络在**进行匹配时能够同时考虑到特征描述和位置的相似性**,了解Transformer的同学应该想到这其实就是Transformer中普遍用的Positional Encoding。在代码中这个过程如下:
self.kenc = KeypointEncoder(self.descriptor_dim, self.keypoint_encoder)
desc0 = desc0 + self.kenc(kpts0, data['scores0'])
desc1 = desc1 + self.kenc(kpts1, data['scores1'])
classKeypointEncoder(torch.jit.ScriptModule):""" Joint encoding of visual appearance and location using MLPs"""def__init__(self, feature_dim, layers):super().__init__()
self.encoder = MLP([3]+ layers +[feature_dim])
nn.init.constant_(self.encoder[-1].bias,0.0)@torch.jit.script_methoddefforward(self, kpts, scores):
inputs =[kpts.transpose(1,2), scores.unsqueeze(1)]# 注意这里将Score也Concatenate进输入return self.encoder(torch.cat(inputs, dim=1))defMLP(channels:list, do_bn=True):""" Multi-layer perceptron """
n =len(channels)
layers =[]for i inrange(1, n):
layers.append(
nn.Conv1d(channels[i -1], channels[i], kernel_size=1, bias=True))if i <(n-1):if do_bn:
layers.append(nn.BatchNorm1d(channels[i]))
layers.append(nn.ReLU())return nn.Sequential(*layers)
接下来我们就是将特征
(
0
)
x
i
{ }^{(0)} \mathbf{x}_{i}
(0)xi输入进Attention Graph Neural Network,作者在这里定义了两种Graph,分别是连接特征点
i
i
i和**同一张图像内的其他特征点**的无向图
E
self
\mathcal{E}_{\text {self }}
Eself 以及连接特征点
i
i
i与**另一张图像内的特征点**的无向图
E
cross
\mathcal{E}_{\text {cross }}
Ecross 。我们通过Transformer计算特征点
i
i
i与图
E
\mathcal{E}
E的信息
m
E
→
i
\mathbf{m}_{\mathcal{E} \rightarrow i}
mE→i,这个“信息”是原论文中"message"的直译,可以理解为通过Transformer提取的特征。信息
m
E
→
i
\mathbf{m}_{\mathcal{E} \rightarrow i}
mE→i计算过程如下:
m
E
→
i
=
∑
j
:
(
i
,
j
)
∈
E
α
i
j
v
j
\mathbf{m}_{\mathcal{E} \rightarrow i}=\sum_{j:(i, j) \in \mathcal{E}} \alpha_{i j} \mathbf{v}_{j}
mE→i=j:(i,j)∈E∑αijvj
α
i
j
=
Softmax
j
(
q
i
k
j
)
\alpha_{i j}=\operatorname{Softmax}_{j}\left(\mathbf{q}_{i} \mathbf{k}_{j}\right)
αij=Softmaxj(qikj)其中,
v
j
\mathbf{v}_{j}
vj、
q
i
\mathbf{q}_{i}
qi、
k
j
\mathbf{k}_{j}
kj分别为value、query、key,计算过程如下:
q
i
=
W
1
(
ℓ
)
x
i
Q
+
b
1
\mathbf{q}_{i}=\mathbf{W}_{1}{ }^{(\ell)} \mathbf{x}_{i}^{Q}+\mathbf{b}_{1}
qi=W1(ℓ)xiQ+b1
[
k
j
v
j
]
=
[
W
2
W
3
]
(
ℓ
)
x
j
S
+
[
b
2
b
3
]
\left[\begin{array}{l} \mathbf{k}_{j} \\ \mathbf{v}_{j} \end{array}\right]=\left[\begin{array}{l} \mathbf{W}_{2} \\ \mathbf{W}_{3} \end{array}\right]{ }^{(\ell)} \mathbf{x}_{j}^{S}+\left[\begin{array}{l} \mathbf{b}_{2} \\ \mathbf{b}_{3} \end{array}\right]
[kjvj]=[W2W3](ℓ)xjS+[b2b3]代码如下:
self.attn = MultiHeadedAttention(num_heads, feature_dim)
message = self.attn(x, source, source)
classMultiHeadedAttention(torch.jit.ScriptModule):""" Multi-head attention to increase model expressivitiy """
prob: List[torch.Tensor]def__init__(self, num_heads:int, d_model:int):super().__init__()assert d_model % num_heads ==0
self.dim = d_model // num_heads
self.num_heads = num_heads
self.merge = nn.Conv1d(d_model, d_model, kernel_size=1)
self.proj = nn.ModuleList([deepcopy(self.merge)for _ inrange(3)])# 对应不同的W
self.prob =[]@torch.jit.script_methoddefforward(self, query, key, value):
batch_dim = query.size(0)
query, key, value =[l(x).view(batch_dim, self.dim, self.num_heads,-1)for l, x inzip(self.proj,(query, key, value))]# 通过卷积提取query、key、value
x, prob = attention(query, key, value)# 进行attention计算
self.prob.append(prob)return self.merge(x.contiguous().view(batch_dim, self.dim*self.num_heads,-1))# 合并多头结果defattention(query, key, value):
dim = query.shape[1]
scores = torch.einsum('bdhn,bdhm->bhnm', query, key)/ dim**.5
prob = torch.nn.functional.softmax(scores, dim=-1)return torch.einsum('bhnm,bdhm->bdhn', prob, value), prob
得到信息
m
E
→
i
\mathbf{m}_{\mathcal{E} \rightarrow i}
mE→i后,我们进一步更新特征:
(
ℓ
+
1
)
x
i
A
=
(
ℓ
)
x
i
A
+
MLP
(
[
(
ℓ
)
x
i
A
∥
m
E
→
i
]
)
{ }^{(\ell+1)} \mathbf{x}_{i}^{A}={ }^{(\ell)} \mathbf{x}_{i}^{A}+\operatorname{MLP}\left(\left[(\ell) \mathbf{x}_{i}^{A} \| \mathbf{m}_{\mathcal{E} \rightarrow i}\right]\right)
(ℓ+1)xiA=(ℓ)xiA+MLP([(ℓ)xiA∥mE→i])其中
(
ℓ
)
x
i
A
{ }^{(\ell)} \mathbf{x}_{i}^{A}
(ℓ)xiA为第
l
l
l 层图像
A
A
A上特征点
i
i
i对应的特征,
[
⋅
∥
⋅
]
[\cdot \| \cdot]
[⋅∥⋅]表示的Concatenate操作,值得注意的是,当
l
l
l 为为奇数时计算的
E
self
\mathcal{E}_{\text {self }}
Eself 的信息,而
l
l
l 为偶数时计算的是
E
cross
\mathcal{E}_{\text {cross }}
Ecross 的信息。这部分代码如下所示:
desc0, desc1 = self.gnn(desc0, desc1)
self.gnn = AttentionalGNN(self.descriptor_dim, self.GNN_layers)
classAttentionalGNN(torch.jit.ScriptModule):def__init__(self, feature_dim:int, layer_names:list):super().__init__()
self.layers = nn.ModuleList([
AttentionalPropagation(feature_dim,4)for _ inrange(len(layer_names))])
self.names = layer_names
@torch.jit.script_methoddefforward(self, desc0, desc1):for i, layer inenumerate(self.layers):
layer.attn.prob =[]if self.names[i]=='cross':
src0, src1 = desc1, desc0
else:# if name == 'self':
src0, src1 = desc0, desc1
delta0, delta1 = layer(desc0, src0), layer(desc1, src1)
desc0, desc1 =(desc0 + delta0),(desc1 + delta1)# 这里相当于residual相加return desc0, desc1
classAttentionalPropagation(torch.jit.ScriptModule):def__init__(self, feature_dim:int, num_heads:int):super().__init__()
self.attn = MultiHeadedAttention(num_heads, feature_dim)
self.mlp = MLP([feature_dim*2, feature_dim*2, feature_dim])
nn.init.constant_(self.mlp[-1].bias,0.0)@torch.jit.script_methoddefforward(self, x, source):
message = self.attn(x, source, source)return self.mlp(torch.cat([x, message], dim=1))# 这里就是上文公式对应的代码计算
这里反复迭代Self-/Cross-Attention的目的原论文指出是为了模拟人类进行匹配时来回浏览的过程,其实Self-Attention为了使得特征更加具备匹配的特异性,而Cross-Attention是为了这些具备特异性的点在图像间进行相似度比较。这个过程在原论文中作者有很好的可视化出来,如下图所示: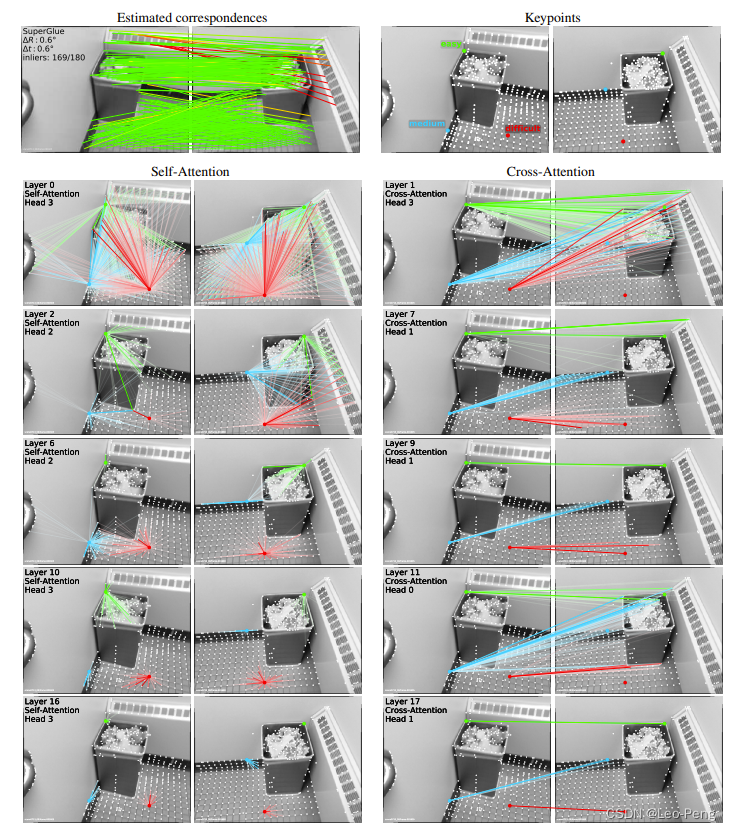
其中,绿色、蓝色和红色分别代表匹配简单、中等和困难的特征点,从左侧Self-Attention的可视化结果我们可以看出,在浅层时,特征点关联到了图像上所有的特征的,而随着网络层数的增加,Self-Attention逐渐收敛到和自己最相似的特征点(包括位置和特征描述),而Cross-Attention表现也是相同的,随着网络层数的增加逐渐收敛到正确匹配点。而且我们可以观察到,绿色的特征点更容易收敛,且关注的区域会随着网络的层数增加而减小。
在完成Attention Graph Neural Network计算后,我们对所有特征点的特征进行一层MLP构建最终我们匹配用的Score矩阵
S
i
,
j
\mathbf{S}_{i, j}
Si,j:
f
i
A
=
W
⋅
(
L
)
x
i
A
+
b
,
∀
i
∈
A
\mathbf{f}_{i}^{A}=\mathbf{W} \cdot{ }^{(L)} \mathbf{x}_{i}^{A}+\mathbf{b}, \quad \forall i \in \mathcal{A}
fiA=W⋅(L)xiA+b,∀i∈A
f
i
B
=
W
⋅
(
L
)
x
i
B
+
b
,
∀
i
∈
B
\mathbf{f}_{i}^{B}=\mathbf{W} \cdot{ }^{(L)} \mathbf{x}_{i}^{B}+\mathbf{b}, \quad \forall i \in \mathcal{B}
fiB=W⋅(L)xiB+b,∀i∈B
S
i
,
j
=
<
f
i
A
,
f
j
B
>
,
∀
(
i
,
j
)
∈
A
×
B
,
\mathbf{S}_{i, j}=<\mathbf{f}_{i}^{A}, \mathbf{f}_{j}^{B}>, \forall(i, j) \in \mathcal{A} \times \mathcal{B},
Si,j=<fiA,fjB>,∀(i,j)∈A×B,其中
<
⋅
,
⋅
>
<·, ·>
<⋅,⋅>为点乘操作,对应代码如下:
# Final MLP projection.
mdesc0, mdesc1 = self.final_proj(desc0), self.final_proj(desc1)# Compute matching descriptor distance.
scores = torch.einsum('bdn,bdm->bnm', mdesc0, mdesc1)
scores = scores / self.descriptor_dim**.5
self.final_proj = nn.Conv1d(self.descriptor_dim, self.descriptor_dim, kernel_size=1, bias=True)
接下来就是对scores矩阵应用Sinkhorn算法:
scores = log_optimal_transport(
scores, self.bin_score,
iters=self.config['sinkhorn_iterations'])
deflog_sinkhorn_iterations(Z: torch.Tensor, log_mu: torch.Tensor, log_nu: torch.Tensor, iters:int)-> torch.Tensor:""" Perform Sinkhorn Normalization in Log-space for stability"""
u, v = torch.zeros_like(log_mu), torch.zeros_like(log_nu)for _ inrange(iters):
u = log_mu - torch.logsumexp(Z + v.unsqueeze(1), dim=2)
v = log_nu - torch.logsumexp(Z + u.unsqueeze(2), dim=1)return Z + u.unsqueeze(2)+ v.unsqueeze(1)deflog_optimal_transport(scores: torch.Tensor, alpha: torch.Tensor, iters:int)-> torch.Tensor:""" Perform Differentiable Optimal Transport in Log-space for stability"""
b, m, n = scores.shape
one = scores.new_tensor(1)
ms, ns =(m*one).to(scores),(n*one).to(scores)
bins0 = alpha.expand(b, m,1)
bins1 = alpha.expand(b,1, n)
alpha = alpha.expand(b,1,1)
couplings = torch.cat([torch.cat([scores, bins0],-1),
torch.cat([bins1, alpha],-1)],1)
norm =-(ms + ns).log()
log_mu = torch.cat([norm.expand(m), ns.log()[None]+ norm])
log_nu = torch.cat([norm.expand(n), ms.log()[None]+ norm])
log_mu, log_nu = log_mu[None].expand(b,-1), log_nu[None].expand(b,-1)
Z = log_sinkhorn_iterations(couplings, log_mu, log_nu, iters)
Z = Z - norm # multiply probabilities by M+Nreturn Z
Sinkhorn算法原理在上文中已经介绍过,这里值得注意的一点是算法针对特征匹配失败问题的处理Trick,文章中特别由提到这一部分,如果不考虑特征点匹配失败的情况,那么我们得到的分配矩阵
P
∈
[
0
,
1
]
M
×
N
\mathbf{P} \in[0,1]^{M \times N}
P∈[0,1]M×N应该满足:
P
1
N
≤
1
M
and
P
⊤
1
M
≤
1
N
\mathbf{P} \mathbf{1}_{N} \leq \mathbf{1}_{M} \quad \text { and } \quad \mathbf{P}^{\top} \mathbf{1}_{M} \leq \mathbf{1}_{N}
P1N≤1M and P⊤1M≤1N其中待分配向量
1
M
\mathbf{1}_{M}
1M和
1
N
\mathbf{1}_{N}
1N分别为长度为
M
M
M和
N
N
N,元素值为
1
1
1的向量。为了求得分配矩阵
P
\mathbf{P}
P,我们是通过计算得分矩阵
S
∈
R
M
×
N
\mathbf{S} \in \mathbb{R}^{M \times N}
S∈RM×N获得,但是由于真实环境中存在遮挡或者噪声,总会有特征点匹配不上的情况,为此,作者在得分矩阵添加一行和一列作为Dustbin:
S
‾
i
,
N
+
1
=
S
‾
M
+
1
,
j
=
S
‾
M
+
1
,
N
+
1
=
z
∈
R
\overline{\mathbf{S}}_{i, N+1}=\overline{\mathbf{S}}_{M+1, j}=\overline{\mathbf{S}}_{M+1, N+1}=z \in \mathbb{R}
Si,N+1=SM+1,j=SM+1,N+1=z∈R此时,待分配向量拓展为
a
=
[
1
M
⊤
N
]
⊤
\mathbf{a}=\left[\begin{array}{ll}\mathbf{1}_{M}^{\top} & N\end{array}\right]^{\top}
a=[1M⊤N]⊤和
b
=
[
1
N
⊤
M
]
⊤
\mathbf{b}=\left[\begin{array}{ll}\mathbf{1}_{N}^{\top} & M\end{array}\right]^{\top}
b=[1N⊤M]⊤,且分配矩阵满足:
P
‾
1
N
+
1
=
a
and
P
‾
⊤
1
M
+
1
=
b
\overline{\mathbf{P}} \mathbf{1}_{N+1}=\mathbf{a} \quad \text { and } \quad \overline{\mathbf{P}}^{\top} \mathbf{1}_{M+1}=\mathbf{b}
P1N+1=a and P⊤1M+1=b其实这也很好理解,对于待匹配点,要求其最多只能与另一个匹配点匹配,但是对于Dustbin,最多能够
M
M
M或者
N
N
N个匹配点与之对应,也就是说最坏的情况就是所有的匹配点都没有匹配上。
2.3 损失函数和网络训练
SuperGlue的损失函数如下所示:
Loss
=
−
∑
(
i
,
j
)
∈
M
log
P
‾
i
,
j
−
∑
i
∈
I
log
P
‾
i
,
N
+
1
−
∑
j
∈
J
log
P
‾
M
+
1
,
j
\begin{aligned} \text { Loss }=&-\sum_{(i, j) \in \mathcal{M}} \log \overline{\mathbf{P}}_{i, j} -\sum_{i \in \mathcal{I}} \log \overline{\mathbf{P}}_{i, N+1}-\sum_{j \in \mathcal{J}} \log \overline{\mathbf{P}}_{M+1, j} \end{aligned}
Loss =−(i,j)∈M∑logPi,j−i∈I∑logPi,N+1−j∈J∑logPM+1,j其中
M
=
{
(
i
,
j
)
}
⊂
A
×
B
\mathcal{M}=\{(i, j)\} \subset \mathcal{A} \times \mathcal{B}
M={(i,j)}⊂A×B为匹配点的真值,
I
⊆
A
\mathcal{I} \subseteq \mathcal{A}
I⊆A和
J
⊆
B
\mathcal{J} \subseteq \mathcal{B}
J⊆B为图像
A
A
A和
B
B
B中没有匹配上的特征点。
关于网络的训练文章在论文的附录中有提到:
(1)基于带有Depth和位姿真值的数据集获取真值,基本方法是通过使用SuperPoint或者SIFT分别在已知位姿的两张图像进行特诊检测,根据Depth将一张图像的特征点投影到另一张图像上,通过重投影误差判断哪些点是匹配成功的点作为真值的正样本。对于负样本,也就是没有匹配上的点,要求重投影误差大于一定的值。
(2)SuperGlue对Indoor、Outdoor和Homograpy变换场景分别训练,Indoor、Outdoor场景训练使用Homograpy变换的模型作为处置。
(3)SuperGlue和SuperPoint的联合训练中,分别使用了两个SuperPoint网络分别进行检测和特征提取的工作,在训练过程中,检测部分的网络权重锁住,只训练特征提取部分的网络。
以上就完成SuperPoint和SuperGlue的总结,除了SuperPoint和SuperGlue,这两年使用NN做特征匹配的方法也有不少,比如:
《OpenGlue: Open Source Graph Neural Net Based Pipeline for Image Matching》
匹配速度更快;
《LoFTR: Detector-Free Local Feature Matching with Transformers》
无特征匹配,对于若纹理区域效果特别好;
《MatchFormer: Interleaving Attention in Transformers for Feature Matching》
改进的LoFTR, 将Attention引入特征编码阶段,大幅度提升特征匹配在大视角变化时的匹配性能
这些算法之后有时间可以再整理下,有问题欢迎交流~
版权归原作者 Leo-Peng 所有, 如有侵权,请联系我们删除。