机器学习西瓜书要点归纳
目录地址
第3章 线性模型
3.1 基本形式
线性模型定义:
其中x是输入向量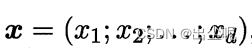
优点:形式简单,易于建模,可解释性好。
3.2 线性回归
输入预处理:连续值可以直接用,离散值若有序,可以按序赋值变连续(如“高,中,低”变为“1,0.5,0”,否则可以单热点码编码。
回归常用MSE,要偏导数为0,当输入是一维时可以算出来: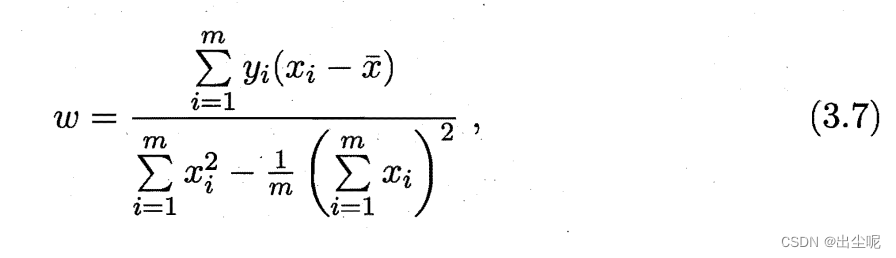
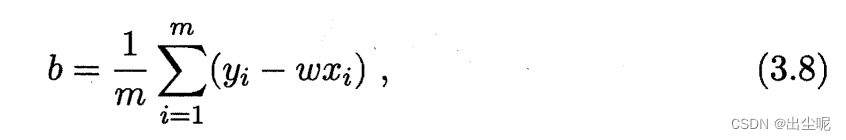
当多元时,矩阵求导,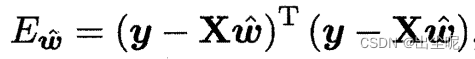
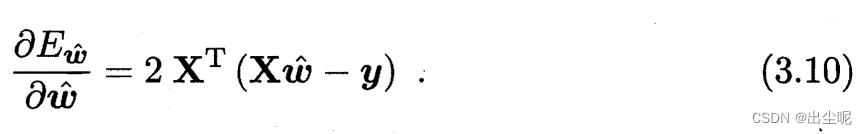
矩阵微分公式见南瓜书
原理可见:链接
当
X
T
X
X^TX
XTX满秩,即可逆,可解得:
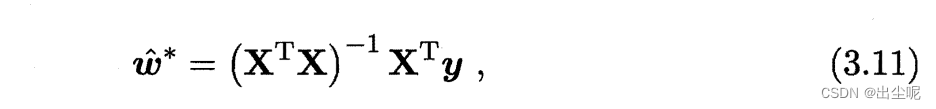
当不满秩,有多解,常见是奥卡姆剃刀式引入正则化找简单的,具体根据学习算法偏好决定。
广义线性模型:
这样子,是拟合
g
(
y
)
g(y)
g(y)。
3.3 对数几率回归
用于二分类任务。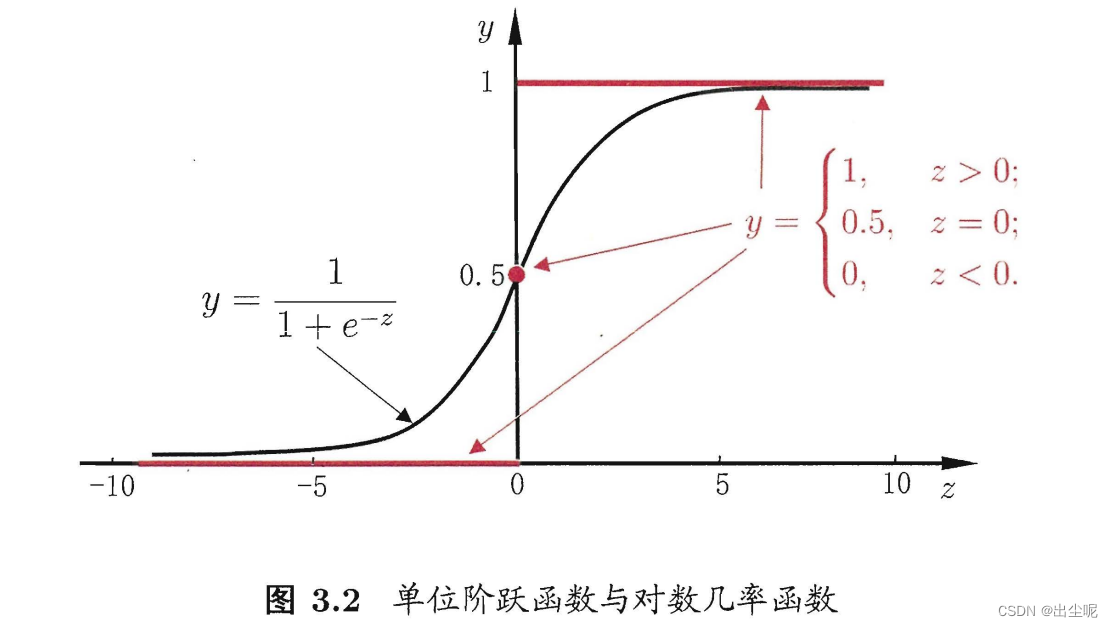
二分类,理想的函数是红线的二分类函数,但是不可导,
所以要找替代函数(surrogate function),例如黑线:
对数几率函数(logistic function):
此时的形式为: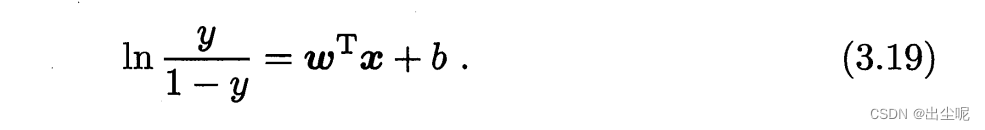
也可以为闭式解。
可以理解为,
y
y
y是正例概率,
1
−
y
1-y
1−y是反例概率,y/(1-y)就是正例比反例更可能的概率。
绿线是给定y的y/(1-y),蓝线是给定y的ln[y/(1-y)],
期望输入一个x,线性模型可以得到一个合适的y。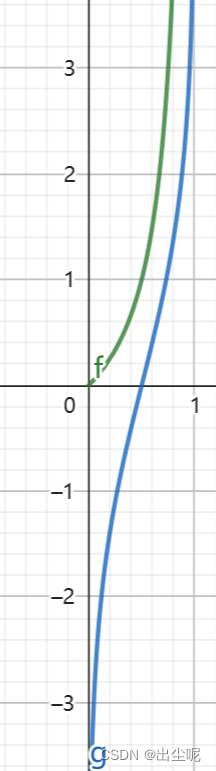
求解时,可以用极大似然估计,也就是把每个样本的标签对应的预测求和,让这个和尽可能大。
每个样本都是让下式尽可能接近于1: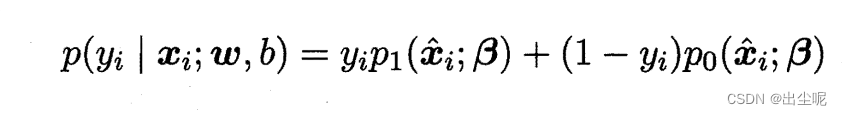
β
\beta
β是要优化的参数,
则是最小化: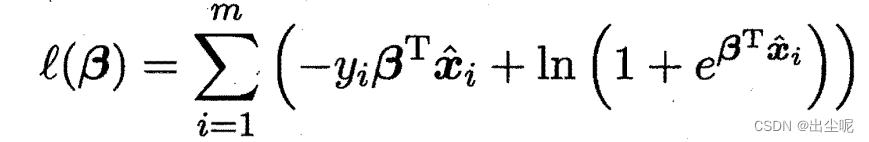
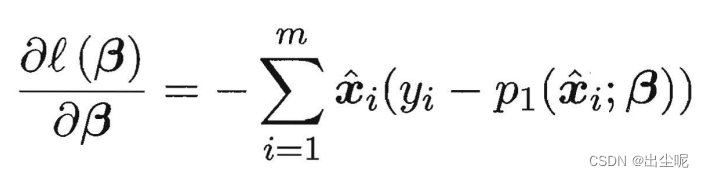
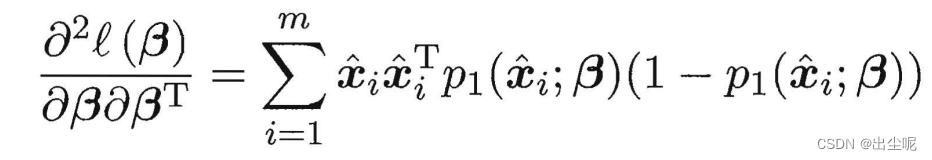
二阶导大于0,这是个凸函数,可以梯度下降法或牛顿法等求和。
3.4 线性判别分析
线性判别分析(Linear Discriminant Analysis, LDA):一种二分类方法。
LDA思想:对训练集,设法将样例投影到一条直线上,使得同类样例的投影点尽可能接近,不同类样例的投影点尽可能远离;对测试集,投影到该直线,根据投影点的位置确定新样本的类别。
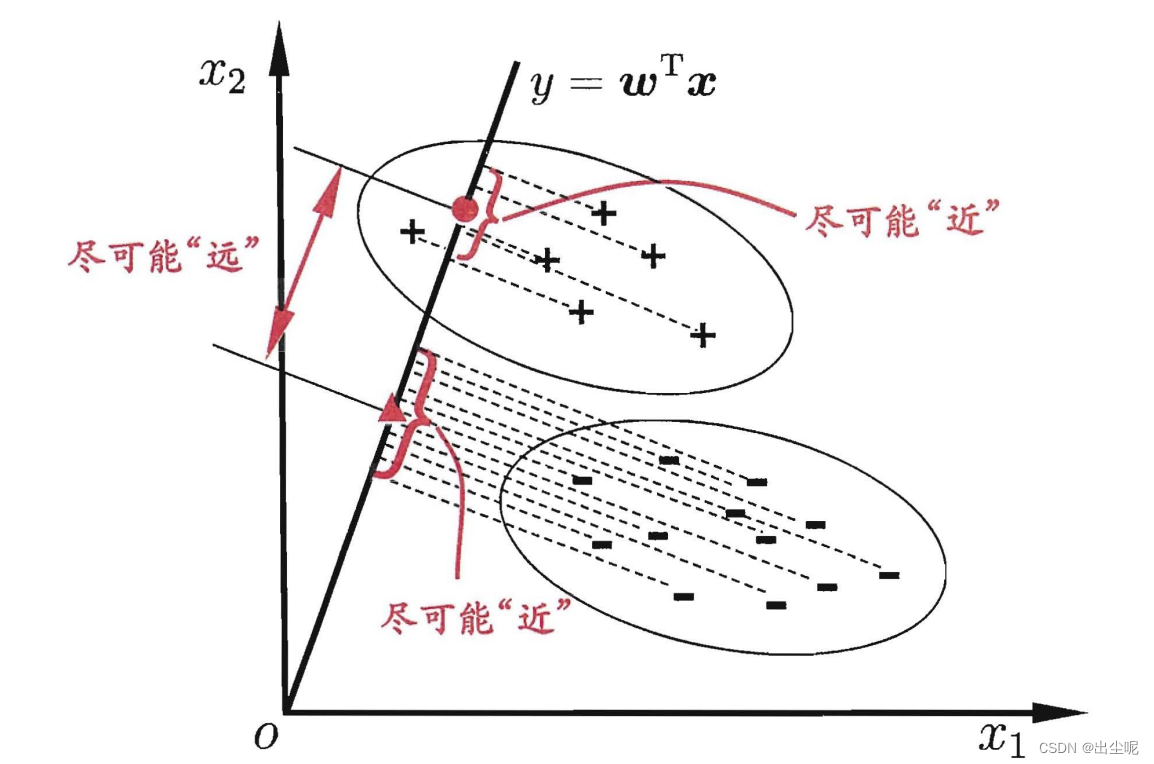
具体方法:
直线就是
y
=
w
x
y=wx
y=wx,x是输入w是参数。
要让正例
y
0
y_0
y0和反例
y
1
y_1
y1的平均值尽可能大,让正反例内的方差尽可能小:
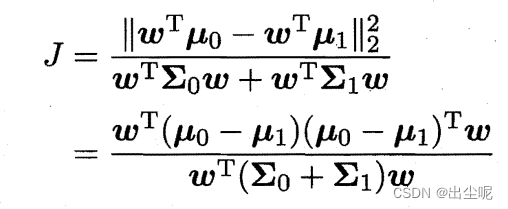
也就是让J尽可能大,
μ
\mu
μ是平均值向量,
Σ
\Sigma
Σ是协方差矩阵。
定义
类内散度矩阵(within-class scatter matrix):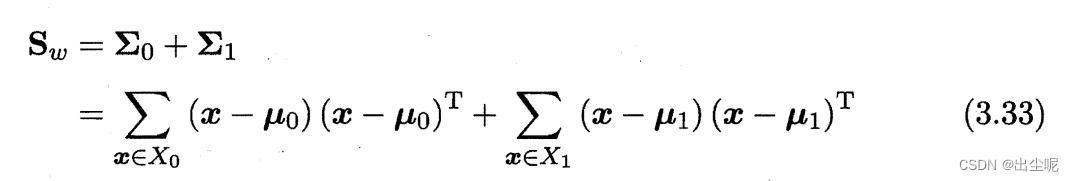
类间散度矩阵(between-class scatter matrix):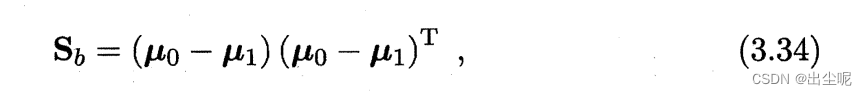
则
J恰好是
S
b
,
S
w
S_b,S_w
Sb,Sw的广义瑞利商(generalized Rayleigh quotient)。
优化方法:
该商只与w方向有关,与w大小无关。
则不妨让分母为1,优化分子:
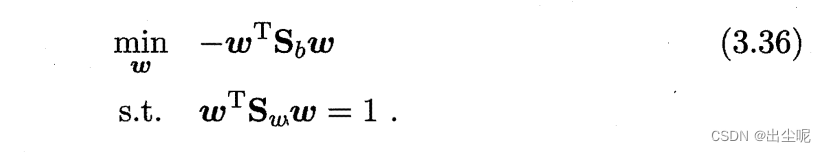
拉格朗日乘子法(具体见南瓜书)得:
注意,
λ
\lambda
λ只是希望约束和值相切,即垂线平行的,取值不重要,
又由于
S
b
w
S_bw
Sbw的方向是
μ
0
−
μ
1
\mu_0-\mu_1
μ0−μ1(因为后面的
(
μ
0
−
μ
1
)
T
w
(\mu_0-\mu_1)^Tw
(μ0−μ1)Tw是标量),所以只要数乘该方向向量
λ
(
μ
0
−
μ
1
)
\lambda(\mu_0-\mu_1)
λ(μ0−μ1)即可了。
可得:
S
w
S_w
Sw常用奇异值分解表示,为了追求数值稳定性。
可从贝叶斯决策理论角度阐述,可以证明,数据同先验、满足高斯分布且协方差相等,LDA可达最优分类。
推广到多分类任务:
定义: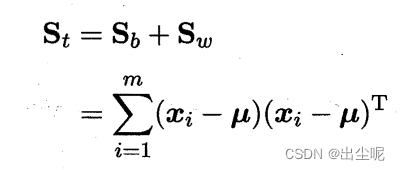
Sb变为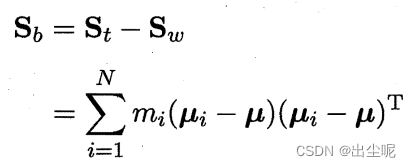
(和之前N=2时的定义相比,只会差一个权重系数
m
1
m
2
/
(
m
1
+
m
2
)
m_1m_2/(m_1+m_2)
m1m2/(m1+m2),不影响优化结果)
优化目标可为: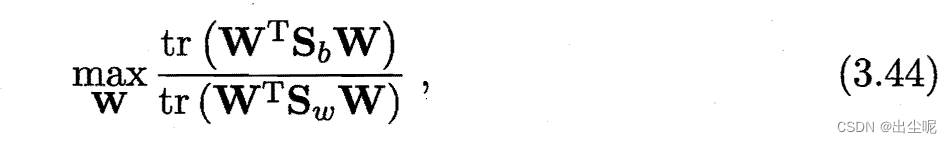
tr是各对角线元素之和,最后
W
T
X
W^TX
WTX是一个
N
−
1
N-1
N−1维的向量,N是类别数。
则
这次的推导也是看南瓜书,原理看链接
W的解是
S
w
−
1
S
b
S_w^{-1}S_b
Sw−1Sb的前N-1个最大的广义特征值对应的特征向量,是最小化损失的有损压缩。
d维变成N-1维的向量,也可以作为降维的方法,可以把维度改为任意的d’而不必是N-1,但是
d ′ ≤ N − 1 d'\le N-1 d′≤N−1因为Sb的秩就是N-1。原因可参考链接,也可以在n=2时验证,理解了2个类别秩为1可以数学归纳法。
之后还是做投影,看和哪个类的距离最近。
3.5 多分类学习
本节介绍了3种模式,通过二分类器达到多分类的目的。
一对一(One vs. One,OvO)
一对其余(One vs. Rest,OvR)
多对多(Many vs. Many,MvM)
OvO和OvR: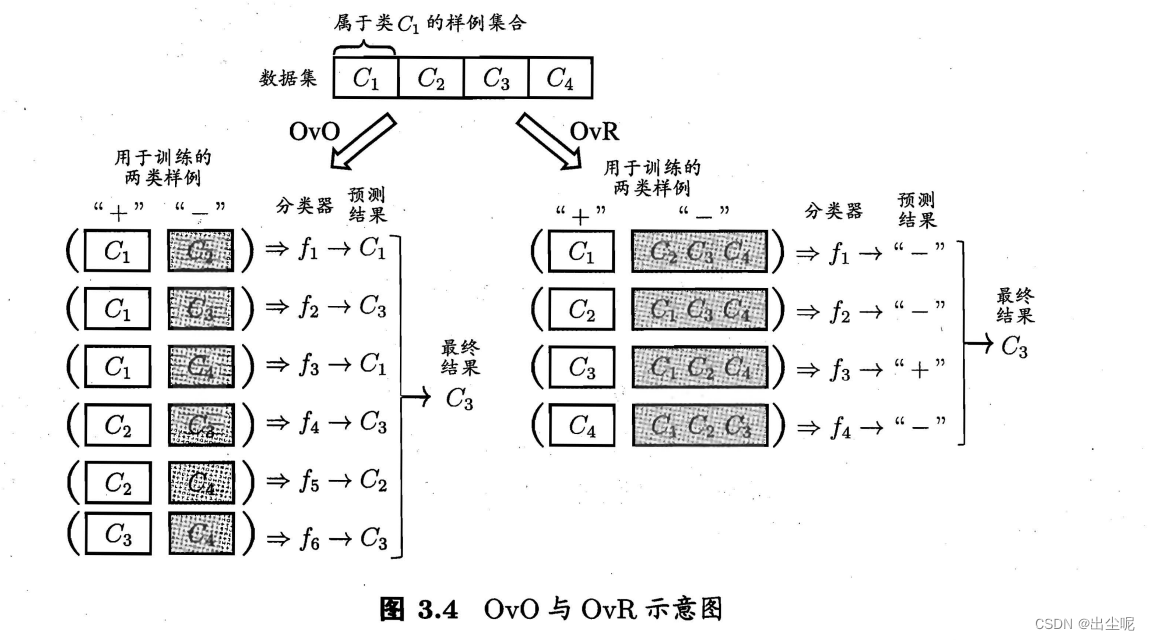
MvM之一:纠错输出码(Error Correcting Output Codes,ECOC)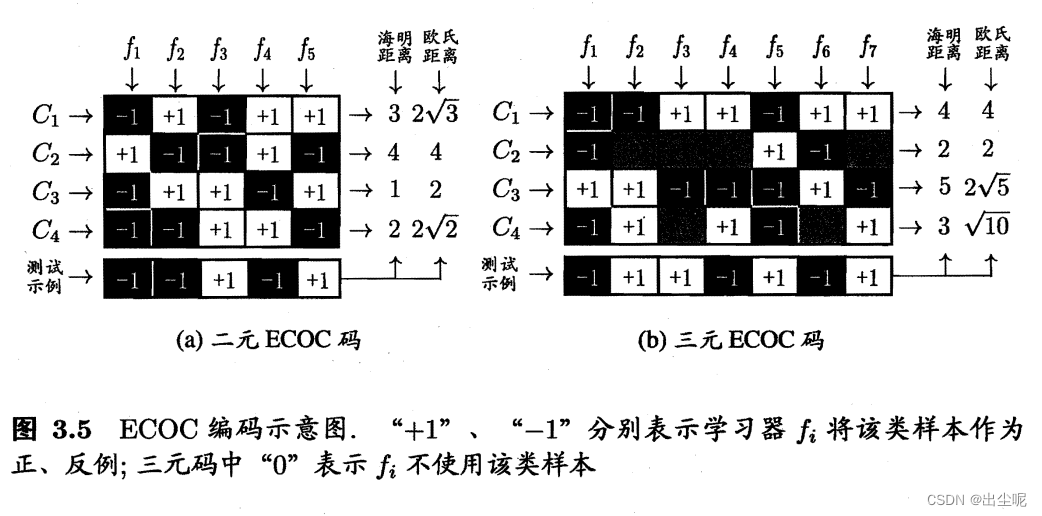
C是类别的编码,f是分类器。
还有DAG形式的MvM等。
3.6 类别不平衡问题
对于二分类,因为y/(1-y)是正例/负例出现的概率。
令m+、m-分别是正负例样本数,那么期望概率是m+/m-的时候,要有以m+/m-为阈值而不是原来的1,即: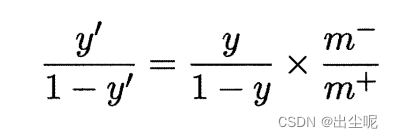
具体做法除了以上的“阈值移动(threshold-moving)”,还有反例“欠采样(undersampling)”(这常常结合集成模型防止丢失主要信息),正例“过采样(oversampling)”(这常常使用插值等方法数据增强缓解过拟合)。
此外,令期望出现正例的概率是cost-/cost+也可以作为代价敏感学习的方法,当cost-小时多预测为负,反之亦然。
3.7 阅读材料
习题
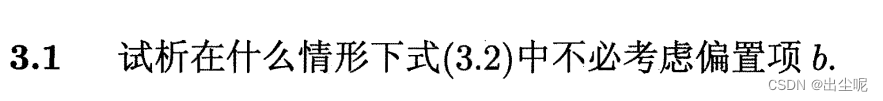

当全0向量输入时输出应该是0时。


反证法:当b=0,x=1,就是sigmoid函数,显然非凸。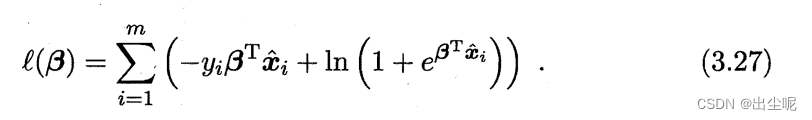
在书中二阶导>0。
牛顿迭代法:
import numpy as np
import pandas as pd
Set = pd.read_csv("data.csv")# 数据集
X = np.array(Set[['密度','含糖率']])# 标签
Y = np.where(np.array(Set[['好瓜']])=='是',1,0)
N,Dy = Y.shape
X = np.append(X,np.ones(N).reshape(N,1),axis=1)
_,Dx = X.shape
X=X.T
Y=Y.T
Beta = np.random.random(size=(Dx,1))
T =10for t inrange(T):
p1=np.exp(Beta.T@X)/(1+np.exp(Beta.T@X))
f1=(-np.sum(X*(Y-p1),axis=1)).reshape(3,1)
f2=(X*p1*(1-p1))@X.T
Beta = Beta - np.linalg.inv(f2)@f1
print('t:',t)print('Beta:',Beta)print('p1:',p1)# 可视化import matplotlib.pyplot as plt
plt.scatter(X[0], X[1], s=10, marker='o')
plt.xlabel('x0')
plt.ylabel('x1')
plt.title('Title')for i inrange(N):
plt.text(X[0][i], X[1][i],"{},{:.3f}".format(Y[0][i],p1[0][i]))
x=np.array([0.2,0.9])
a =-Beta[0][0]/Beta[1][0]# 直线斜率
b =-Beta[2][0]/Beta[1][0]# 直线截距
y_line = a * x + b # 直线方程
plt.plot(x, y_line,'r--')
plt.show()
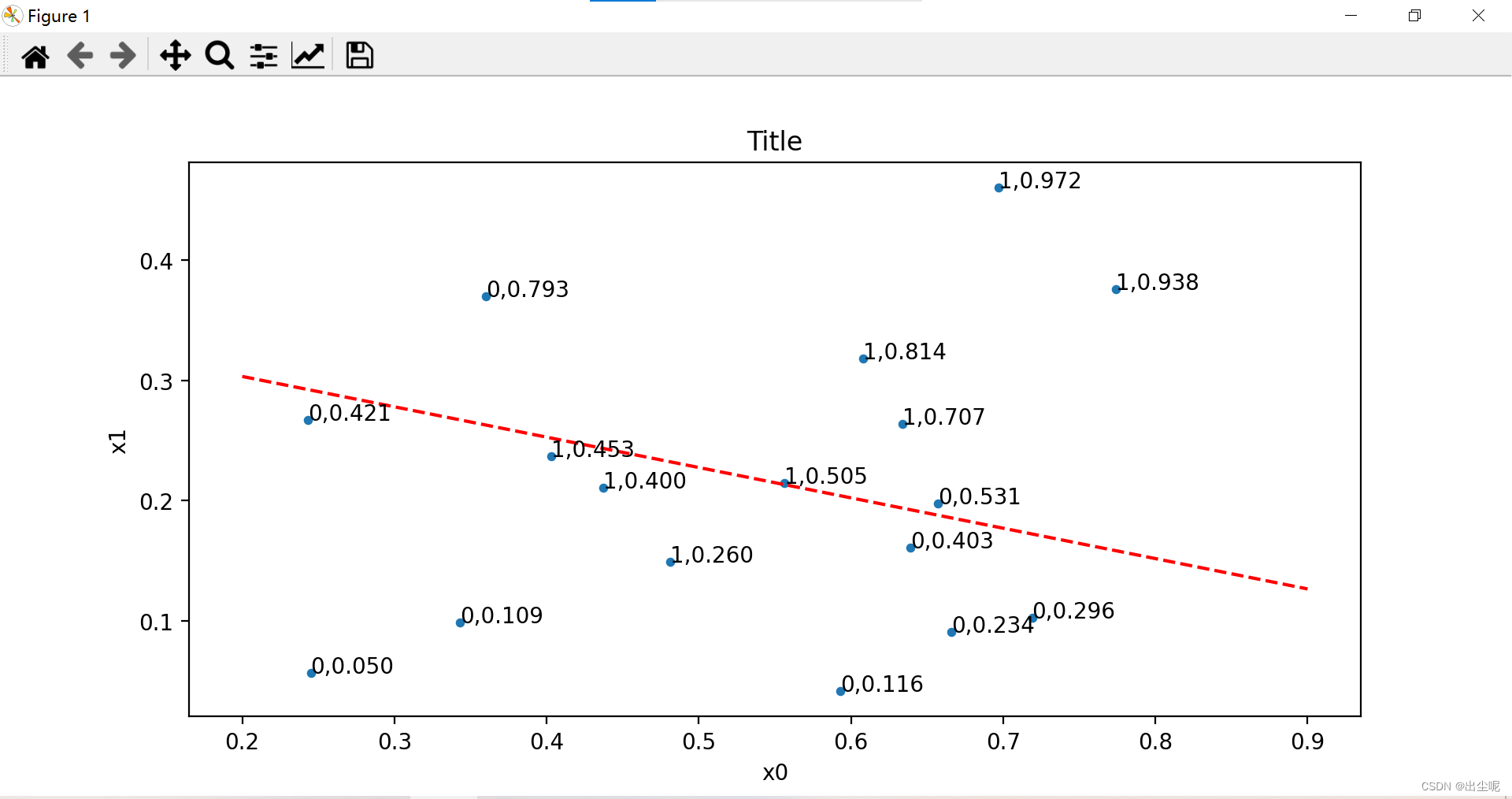
线右上是预测1,左下是预测0.

略
略

参考SVM的核函数。

目标是
m
a
x
(
h
(
c
0
,
c
1
)
+
h
(
c
0
,
c
2
)
+
h
(
c
0
,
c
3
)
+
h
(
c
1
,
c
2
)
+
h
(
c
1
,
c
3
)
+
h
(
c
2
,
c
3
)
)
max(h(c0,c1)+h(c0,c2)+h(c0,c3)+h(c1,c2)+h(c1,c3)+h(c2,c3))
max(h(c0,c1)+h(c0,c2)+h(c0,c3)+h(c1,c2)+h(c1,c3)+h(c2,c3))
h
(
c
i
,
c
j
)
=
s
u
m
(
a
b
s
(
c
i
−
c
j
)
)
h(ci,cj)=sum(abs(ci-cj))
h(ci,cj)=sum(abs(ci−cj))
不失一般性,任意固定c0,其他进行搜索,运算次数O(227)=O(134,217,728),可以暴力枚举。

之所以要满足这个条件,是因为,如果不是,都会带来更加偏好某一个类的效果。
是否满足该条件?
这个要取决于编码的具体方式,不是二分类能决定的。
但是二分类的分类效果也会影响概率,比如数据不均等。
当编码长度冗余,会影响独立性。
因为期望上影响相互抵消。
多分类都可以是二分类的直接套用。
能获得理论最优解,那么"训练集是真实样本总体的无偏采样"要满足。
版权归原作者 出尘呢 所有, 如有侵权,请联系我们删除。
