一、线性卷积:
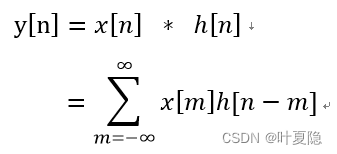
一个输入经过一个线性时不变系统,得到的输出就是线性卷积。
举例:
x[n] = [1, 3, 2, 4];
h[n] = [2, 1, 3];
y[n] = [2, 7, 10, 19, 10, 12];
矩阵表示形式:
输出的长度等于两个输入长度的和减一(L1 + L2 - 1).
二、循环卷积
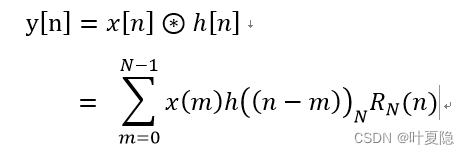
x[n] 和 h[n]都是周期的,下面公式中的h((n-m))不同于线性卷积的翻转,此处为圆周翻装。
(1)N = 4
不够N的需要padding 0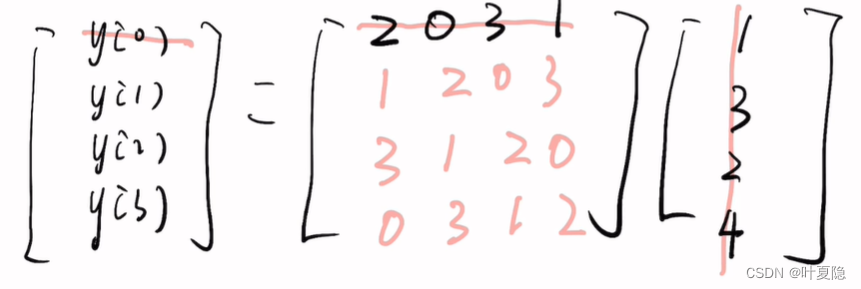
(2) N = 5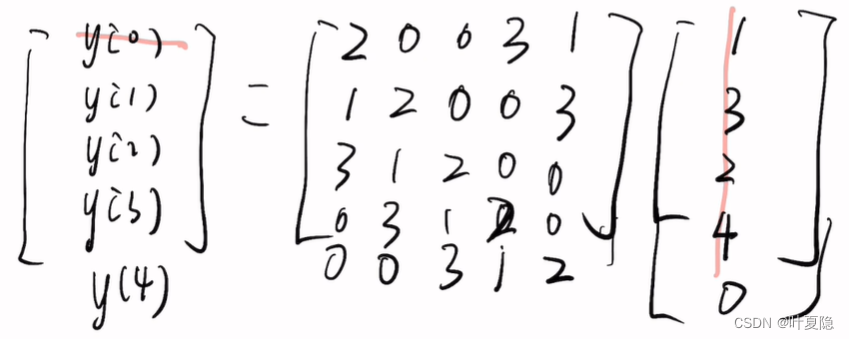
(3) N = 6
y[n] = [2, 7, 10, 19, 10, 12];
由上面可以看出,当N≥L1+L2-1时,线性卷积的结果和圆周卷积结果一致。公式证明:
最后这个公式的意义:
两个信号做线性卷积,然后以圆周卷积的周期L去做延拓,再取周期信号的主值空间(0 … L-1),中间yl线性卷积的长度是L1+L2-1,所以取L去做周期延拓的时候L≥L1+L2-1才不会混叠。


如上图所示:N=4或者5的时候,都发生了混叠,只有N大于等于6,才不会混叠。
三、结论:
N≥L1+L2-1时,线性卷积等于圆周卷积。
四、应用:
DFT:
圆周卷积的性质:时域的圆周卷积等于频域乘积,当计算时域线性卷积时,可以通过圆周卷积的性质,在频域通过简单乘法得到,前提是N≥L1+L2-1,圆周卷积才等于线性卷积。
版权归原作者 叶夏隐 所有, 如有侵权,请联系我们删除。