幼儿园的小朋友会排队做操
小学生们会排队打饭
大妈购物也会抢着“排队”付账
作为程序猿的你,会以下的排序算法吗?

本节目标
1.排序的概念及意义
2.直接插入和希尔排序的实现及分析
3.直接选择和堆排序的实现及分析
首先我们先来看一下基本的七大排序,今天我们先一起学习前四个:
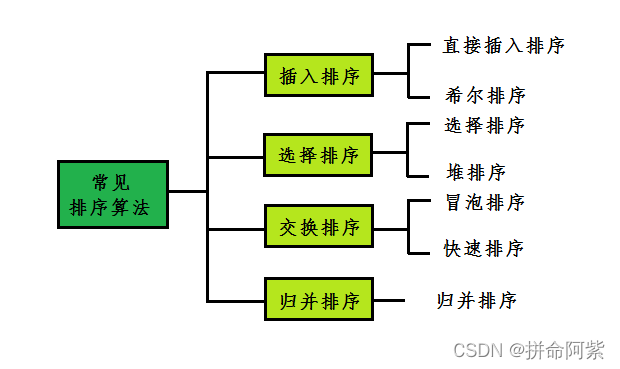
 1、排序的概率及意义
1、排序的概率及意义
** 排序**:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起 来的操作。
稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记 录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍 在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的。
内部排序:数据元素全部放在内存中的排序 。
外部排序:数据元素太多不能同时放在内存中,根据排序过程的要求不能在内外存之间移动数据 的排序。
** 排序的运用**:例如在淘宝购物时我们可以根据综合、销量、好评……进行排序。
 2、直接插入和希尔排序的实现及分析
2、直接插入和希尔排序的实现及分析
2.1.直接插入排序
①基本思想
直接插入排序是一种简单的插入排序法,其基本思想是:把待排序的记录按其关键码值的大小逐 个插入到一个已经排好序的有序序列中,直到所有的记录插入完为止,得到一个新的有序序列 。 实际中我们玩扑克牌时,就用了插入排序的思想:

** ②直接插入排序**
升序:
#include<stdio.h>
void InsertSort(int *a, int n)
{
for (int i = 0; i<n - 1; i++)
{
int end = i;
int tmp = a[end + 1];
while (end >= 0)
{
if (n > 1 && a[end] > tmp)
{
a[end + 1] = a[end];
--end;
}
else
{
break;
}
}
a[end + 1] = tmp;
}
}
void PrintArray(int* a, int n)
{
for (int i = 0; i < n; i++)
{
printf("%d ", a[i]);
}
printf("\n");
}
void TestInsertSort()
{
int a[] = { 1, 3, 2, 6, 8, 7, 9, 4, 5, 0 };
int size = sizeof(a) / sizeof(int);
InsertSort(a, size);
PrintArray(a, size);
}
int main()
{
TestInsertSort();
return 0;
}
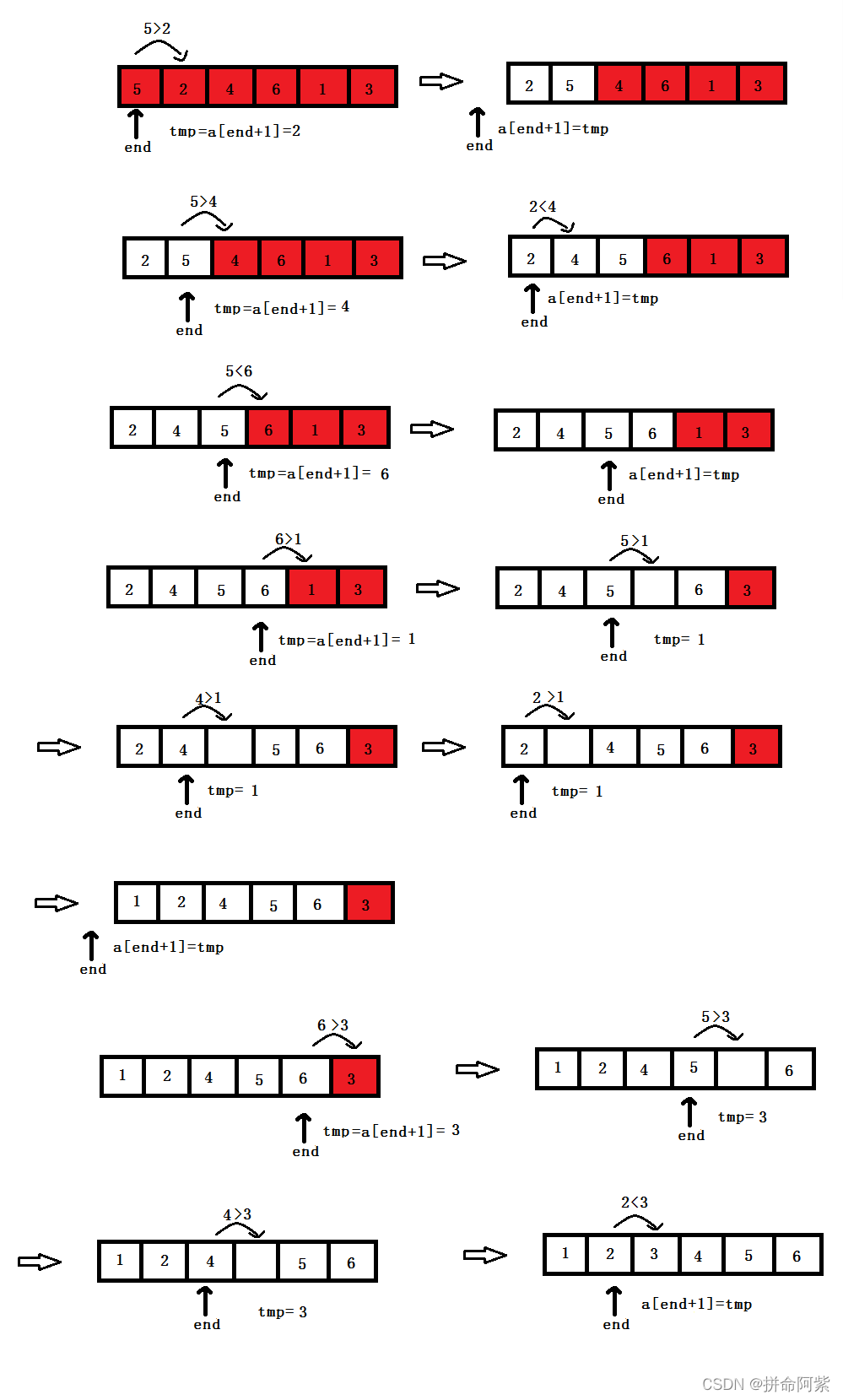
思想: 刚开始执行时,end是数组第一个元素的下标,tmp存放的是end后面一个元素的值,让数组的end下标对应的值与tmp的值进行比较。若为升序,end下标对应的值如果大于tmp中存放的值就交换,然后让end--,然后while循环让end下标对应的值与tmp比较,若end<0就跳出,若end对应下标的值小于tmp要break(避免不必要的比较),跳出内循环后让end+1下标对应数组元素等于tmp。然后使end指向第二个元素的下标,同样的方法依次比较。
总结:
元素集合越接近有序,直接插入排序算法的时间效率越高
时间复杂度:O(N^2)
空间复杂度:O(1),它是一种稳定的排序算法
稳定性:稳定
2.2希尔排序
希尔排序可以说是直接插入排序的进阶版。
希尔排序包含两部分:预排序(接近有序)、 直接插入排序(有序)
希尔排序法又称缩小增量法。希尔排序法的基本思想是:先选定一个整数,把待排序文件中所有 记录分成个组,所有距离为的记录分在同一组内,并对每一组内的记录进行排序。然后,取,重 复上述分组和排序的工作。当到达=1时,所有记录在统一组内排好序。
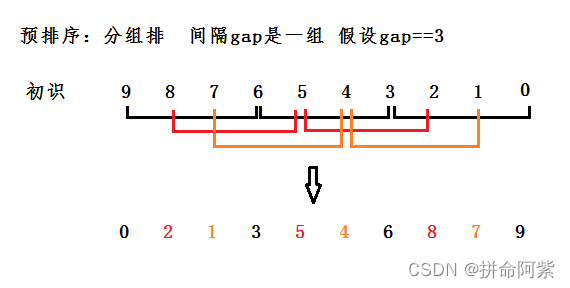
** 观察以下排序:**
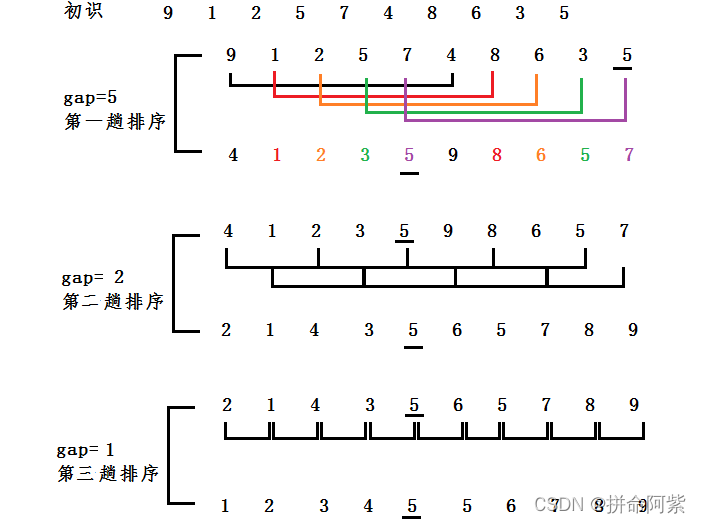
** 多组间隔为gap的预排序,gap有大变小**
gap越大,大的数可以越快的到很后面,小的数可以越快到前面,预排序越不接近有序
gap越小,越接近有序
gap==1时就是直接插入排序
代码:
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
//希尔排序:直接插入排序的基础上的优化
//1、先进行预排序,让数组接近有序(分组排)
//2、直接插入排序
//时间复杂度为log₂N*N或者是log₃N*N
void ShellSort(int* a, int n)
{
int gap = n;
while (gap > 1)
{
//gap = gap / 2; //log₂N
gap = gap / 3 + 1;//log₃N
//gap>1时都是预排序 接近有序
//gap==1时就是直接插入排序 有序
//gap很大时,下面预排序时间复杂度O(n)
//gap很小时,数组已经很接近有序了,这事差不多也是O(n)
//把间隔为gap的多组数据同时排
for (int i = 0; i<n - gap; i++)
{
int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
if (n > 1 && a[end] > tmp)
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}
}
}
void PrintArray(int* a, int n)
{
for (int i = 0; i < n; i++)
{
printf("%d ", a[i]);
}
printf("\n");
}
void TestInsertSort()
{
int a[] = { 1, 3, 2, 6, 8, 7, 9, 4, 5, 0 };
int size = sizeof(a) / sizeof(int);
ShellSort(a, size);
PrintArray(a, size);
}
int main()
{
TestInsertSort();
return 0;
}
希尔排序的特性总结:
① 希尔排序是对直接插入排序的优化
② 当gap > 1时都是预排序,目的是让数组更接近于有序。当gap == 1时,就是直接插入排序。它与直接插入排序的区别就是多了一个预排序,这样使时间效率更好
③ 希尔排序的时间复杂度不好计算,需要进行推导,推导出来平均时间复杂度: O(N^1.3— N^2)
④ 稳定性:不稳定
 3、直接选择和堆排序的实现及分析
3、直接选择和堆排序的实现及分析
选择排序的基本思想: 每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完 。
3.1直接选择排序
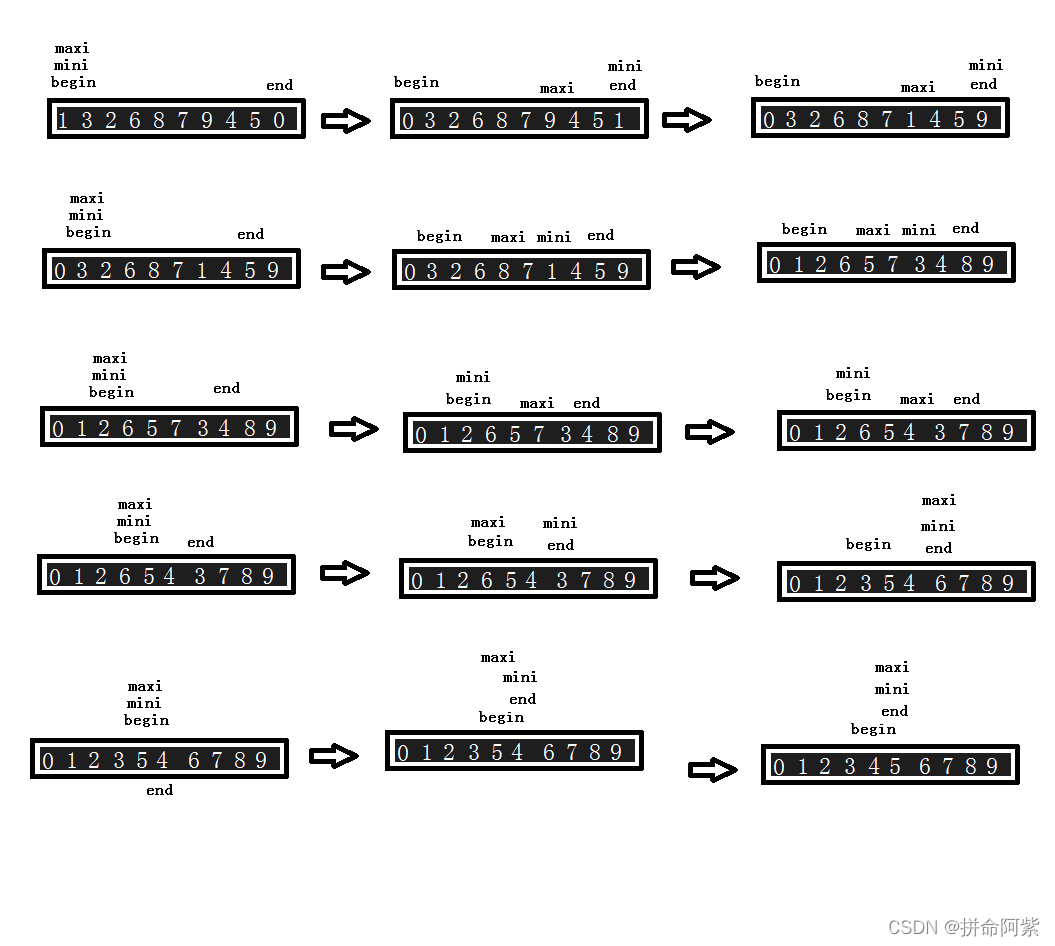
** 代码:**
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
void Swap(int* p1, int* p2)
{
int tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
//直接选择排序
void SelectSort(int* a, int n)
{
int begin = 0, end = n - 1;
while (begin < end)
{
int mini = begin, maxi = begin;
for (int i = begin; i <= end; ++i)
{
if (a[i] < a[mini])
{
mini = i;
}
if (a[i] > a[maxi])
{
maxi = i;
}
}
Swap(&a[mini], &a[begin]);
if (maxi == begin)
{
maxi = mini;
}
Swap(&a[maxi], &a[end]);
begin++;
--end;
}
}
void PrintArray(int* a, int n)
{
for (int i = 0; i < n; i++)
{
printf("%d ", a[i]);
}
printf("\n");
}
void TestInsertSort()
{
int a[] = { 1, 3, 2, 6, 8, 7, 9, 4, 5, 0 };
int size = sizeof(a) / sizeof(int);
SelectSort(a, size);
PrintArray(a, size);
}
int main()
{
TestInsertSort();
return 0;
}
直接选择排序的特性总结:
**1. 直接选择排序思考非常好理解,但是效率不是很好。实际中很少使用 **
**2. 时间复杂度:O(N^2) **
**3. 空间复杂度:O(1) **
4. 稳定性:不稳定
3.2堆排序
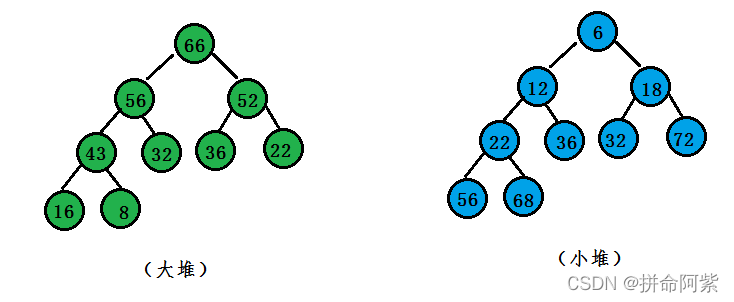
3.2.1堆排序的两大特性
- 结构性:用数组表示的完全二叉树
- 有序性:任一结点的关键字都是其子树所有结点的最大值(或最小值)
- 最大堆,也称大顶堆:最大值
- 最小堆,也称小顶堆:最小值
- 大顶堆的要求:树中所有父亲都大于等于孩子
- 小顶堆的要求:树中所有父亲都小于等于孩子
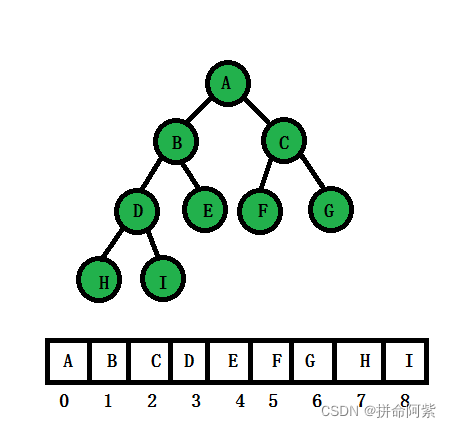
**3.2.2堆物理存储结构及父子关系 **
堆物理存储上是按照数组存储的
完全二叉树是想象出来的
通过下标可以找出父子关系
leftchild=parent*2+1
rightchild=parent*2+1+1=leftchild+1
parent=(child-1)/ 2
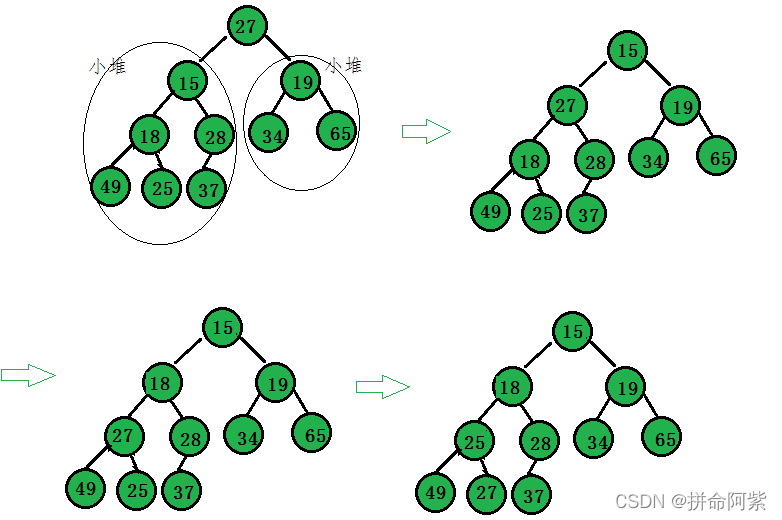
** 3.2.3向下调整算法(前提左右子树必须都为堆)**
** 例:建小堆**
向下调整算法
首先左右子树都必须是小堆
**第一步,先判断左右子树是否都为小堆,要是为小堆就可以进行第二步向下调整算法 **
第二步,向下调整算法,找出根结点的左子树和右子树小的那个,然后与根结点比较如果小于根结点就交换(如果不小于,则这整颗数都是小堆不需要交换)。依次循环,直到找到叶子结点终止
** 要是左右子树不是小堆,就不能直接使用向下调整算法了!怎么办?**
办法:倒着从最后一棵子树开始调,分析倒着走,叶子不需要调,从最后一个非叶子的子树开始调,依次调,让这棵树变成小堆 。
**升序建大堆,因为大堆的根节点是整颗树的最大值 **
**降序建小堆,因为小堆的根节点是整颗树的最小值 **
**把堆建完后就需要排序,将第一个跟最后一个交换,然后把最后一个数不看做堆里面,前n-1个数向下调整选出次大的数,再与倒数第二个位置交换 **
** 代码:**
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
void Swap(int* p1, int* p2)
{
int tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
void AdjustDwon(int* a, int n, int root)
{
int parent = root;
int child = parent * 2 + 1; // 默认是左孩子
while (child < n)
{
// 1、选出左右孩子中大的那一个
if (child + 1 < n && a[child + 1] > a[child])
{
child += 1;
}
if (a[child] > a[parent])
{
Swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
void HeapSort(int* a, int n)
{
// 建堆 O(N)
for (int i = (n - 1 - 1) / 2; i >= 0; --i)
{
AdjustDwon(a, n, i);
}
// 排升序,建大堆还是小堆?建大堆
int end = n - 1;
while (end > 0)
{
Swap(&a[0], &a[end]);
AdjustDwon(a, end, 0);
--end;
}
}
void PrintArray(int* a, int n)
{
for (int i = 0; i < n; i++)
{
printf("%d ", a[i]);
}
printf("\n");
}
void TestInsertSort()
{
int a[] = { 1, 3, 2, 6, 8, 7, 9, 4, 5, 0 };
int size = sizeof(a) / sizeof(int);
HeapSort(a, size);
PrintArray(a, size);
}
int main()
{
TestInsertSort();
return 0;
}
堆排序的特性总结:
- 堆排序使用堆来选数,效率就高了很多。
- 时间复杂度:O(N*logN)
- 空间复杂度:O(1)
- 稳定性:不稳定
版权归原作者 拼命阿紫 所有, 如有侵权,请联系我们删除。