简介
bili 吴恩达 机器学习
这是一门让计算机在没有明确编程的情况下学习的科学。
亚瑟·塞缪尔(1959):赋予计算机学习能力而不被明确编程的研究领域。
机器学习作为人工智能的一个子领域。专门研究计算机怎样模拟或实现人类的学习行为,以获取新的知识或技能,重新组织已有的知识结构使之不断改善自身的性能。它是人工智能核心,是使计算机具有智能的根本途径。
机器学习有下面几种定义:
(1)机器学习是一门人工智能的科学,该领域的主要研究对象是人工智能,特别是如何在经验学习中改善具体算法的性能。
(2)机器学习是对能通过经验自动改进的计算机算法的研究。
(3)机器学习是用数据或以往的经验,以此优化计算机程序的性能标准。
机器学习算法
机器学习算法:
- 监督学习
- 无监督学习
强化学习
监督学习 Supervised Learning
从输入到输出的标签
从被给予“正确答案”中学习
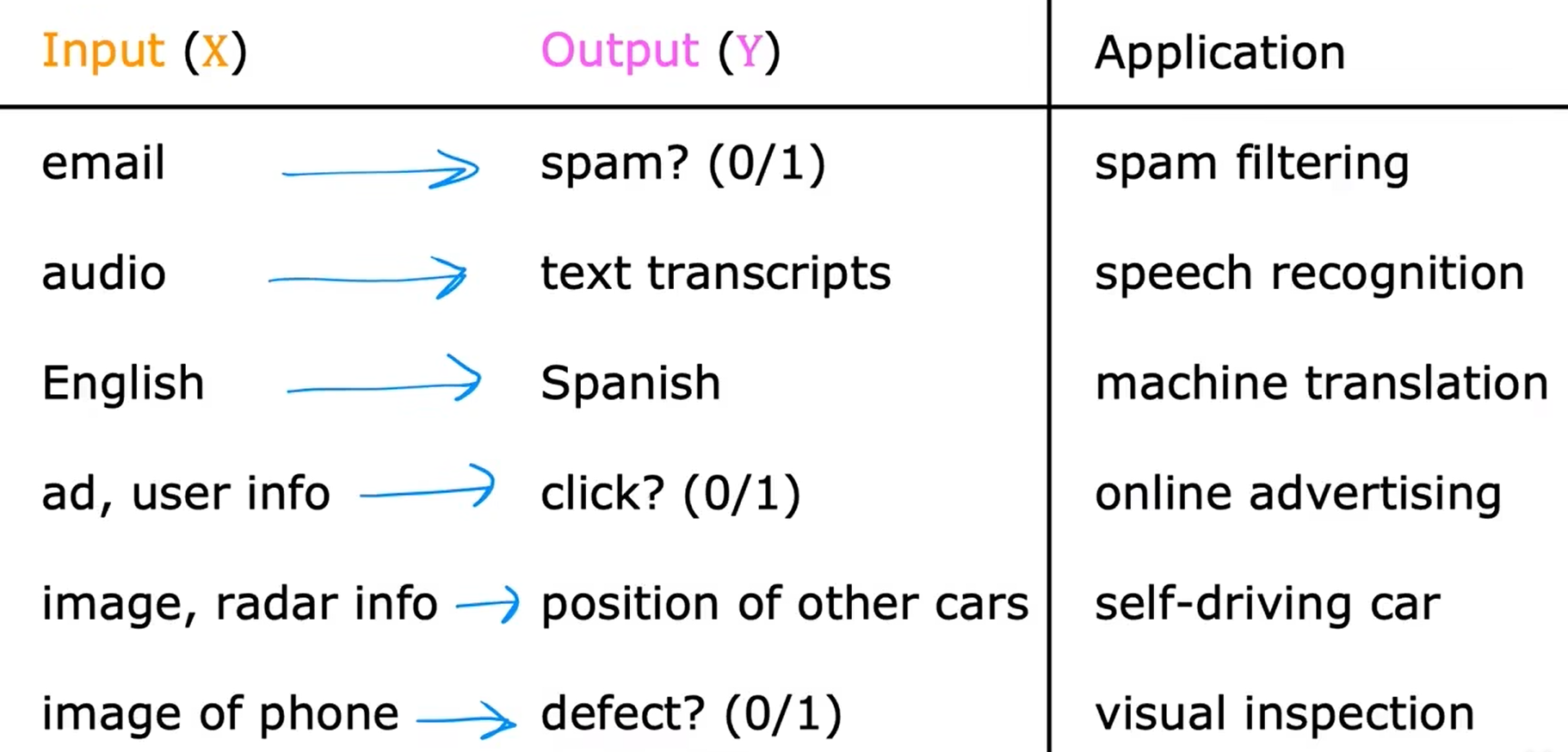
监督学习算法种类:
- 回归 - 回归试图预测无限多个可能的数字中的任何一个。
- 分类 - 分类是指只预测少量可能的输出或类别。

回归 Regression
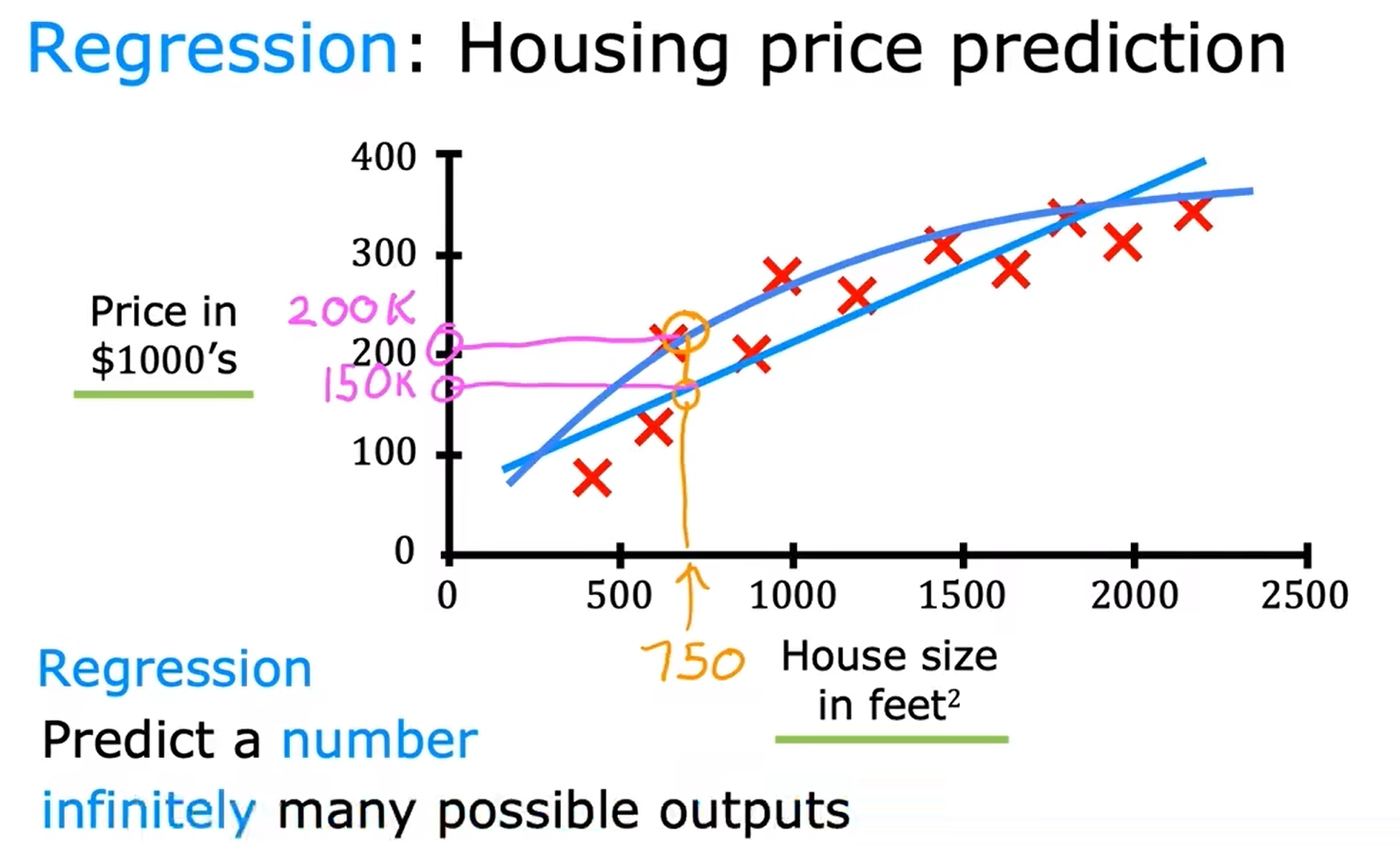
试着从无限多个可能的数字中预测一个数字,例如例子中的房价。
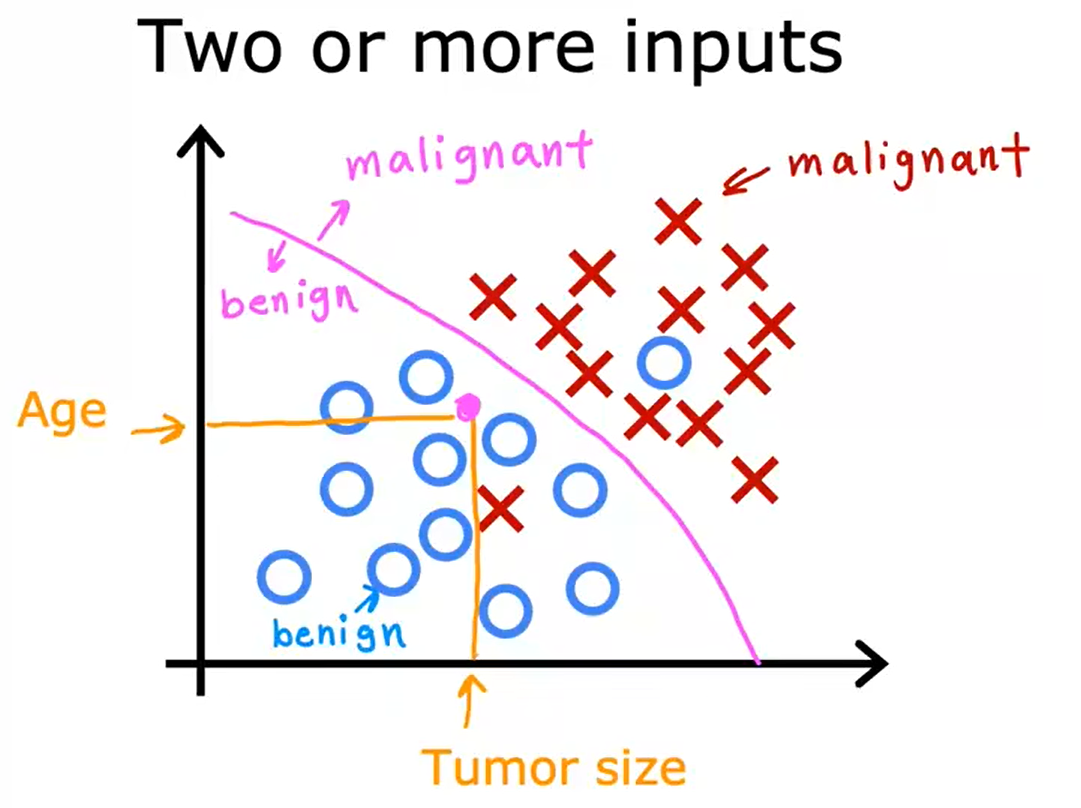
分类 Classification
以乳腺癌检测为例,只有两种可能的输出或两种可能的类别,这就是为什么它被称为分类。
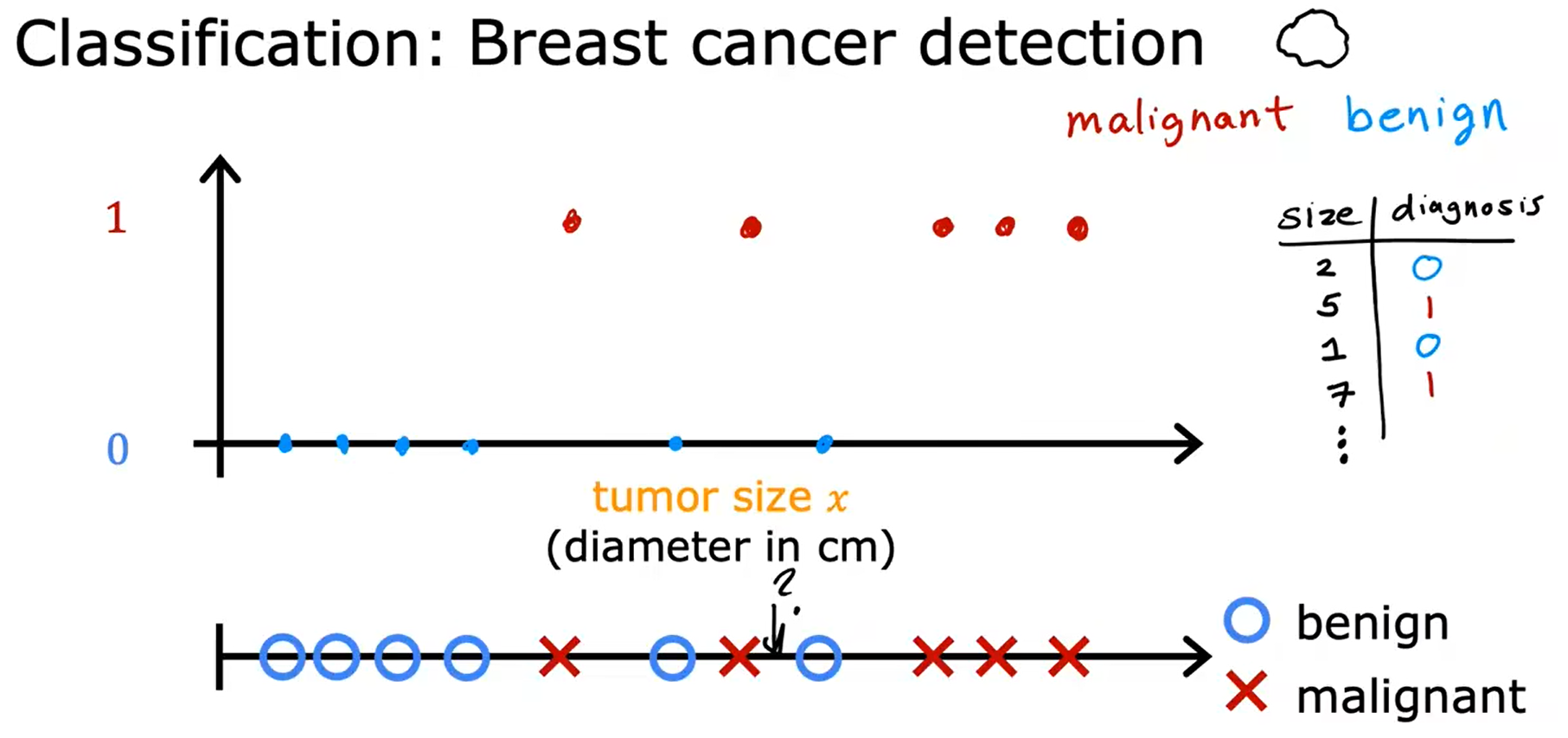
预测类别不一定是数字。
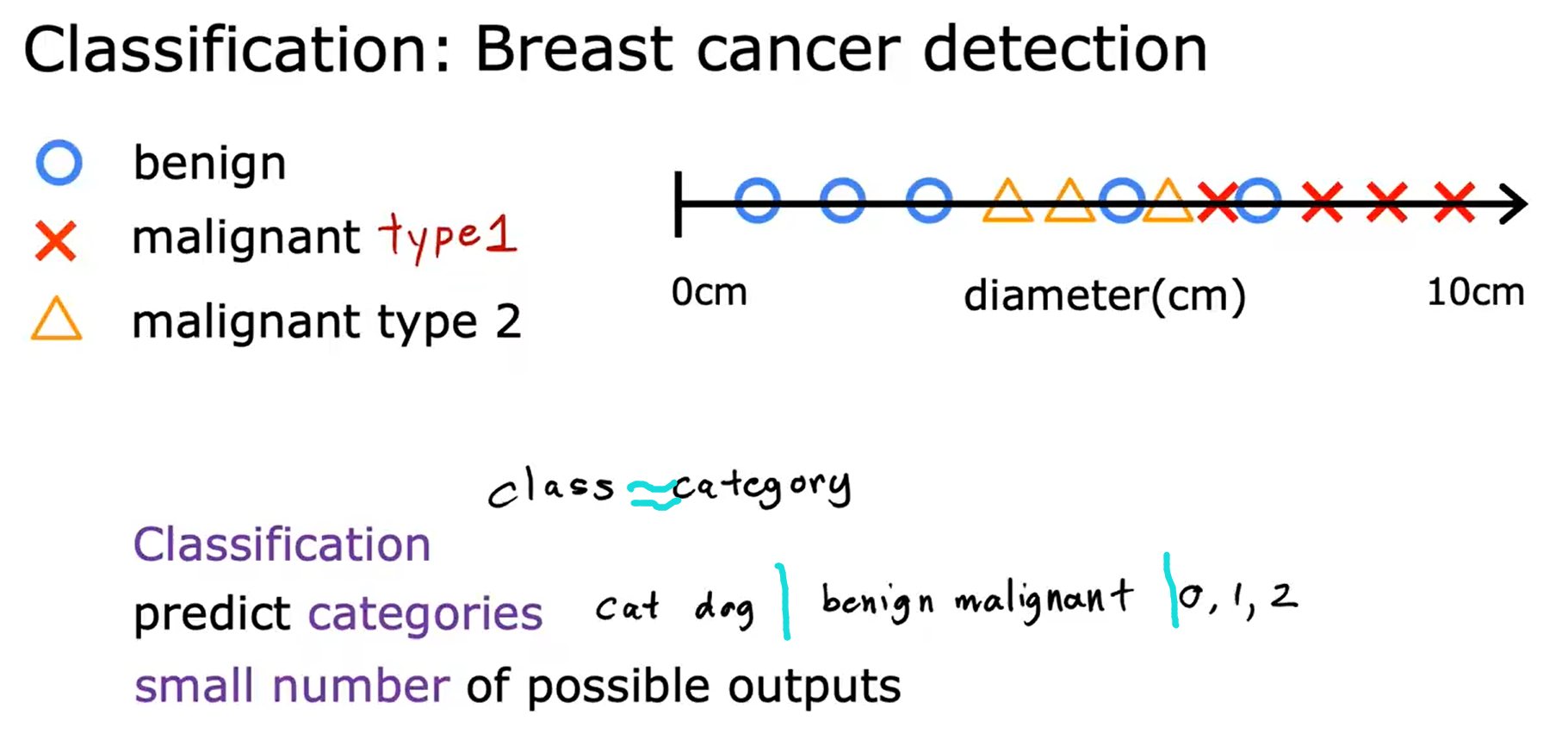
无监督学习 Unsupervised Learning
数据只包含输入x,而不包含输出标签y。
算法必须在数据中找到结构,模式或有趣的东西。
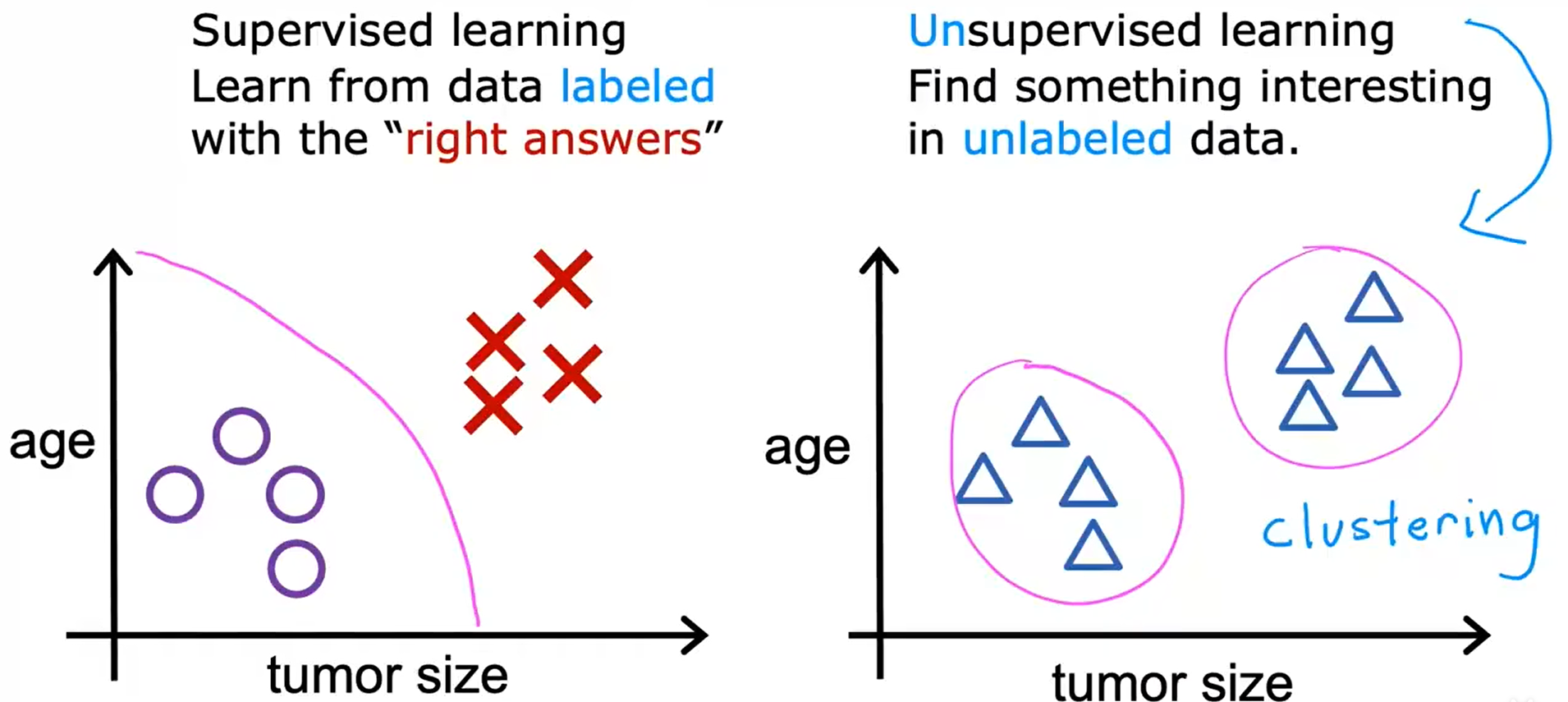
我们不想监督算法并为每一个输入给出引用的正确答案;相反,我们想让算法自己找到一些结构或模式或者只是在数据中找到一些有趣的东西。
无监督学习算法可以决定数据可以分配到两个不同的组或两个不同的集群。
无监督学习分类
- 聚类 - 将相似的数据点分组在一起。
- 异常检测 - 发现异常数据点(金融系统中的欺诈检测)
- 降维 - 使用更少的数字压缩数据,尽可能少的丢失信息
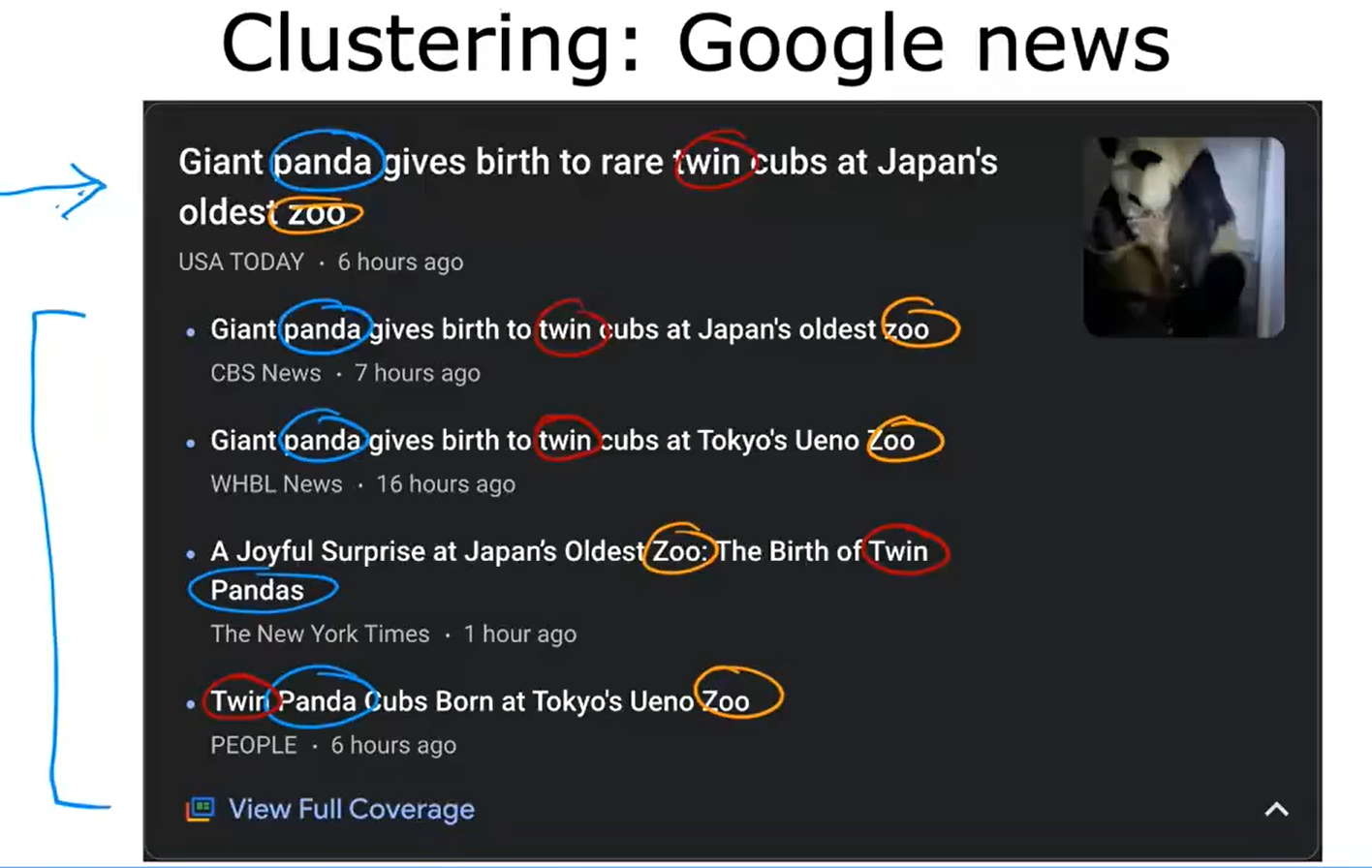
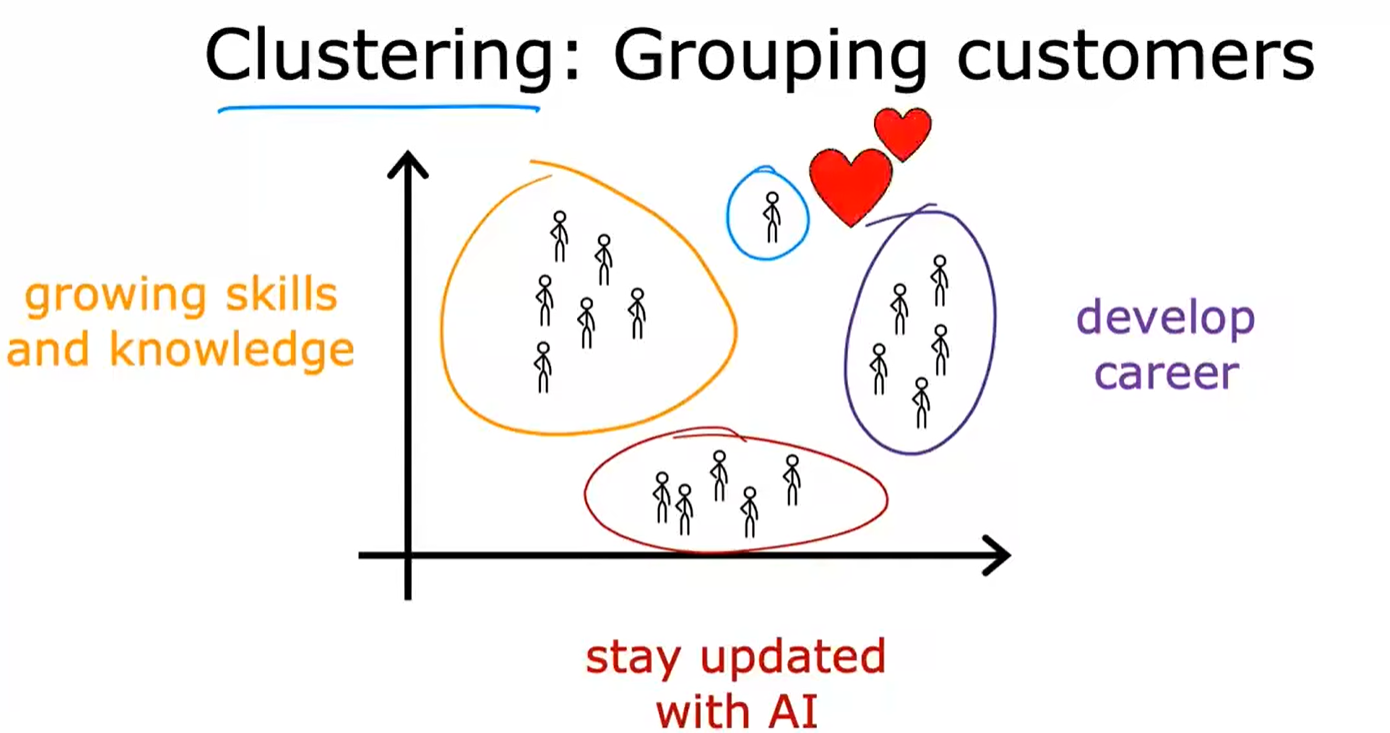
聚类 Clustering
聚类算法是一种无监督学习算法。获取没有标签的数据,并尝试将其自动分组到集群中。

线性回归模型 Linear Regression Model
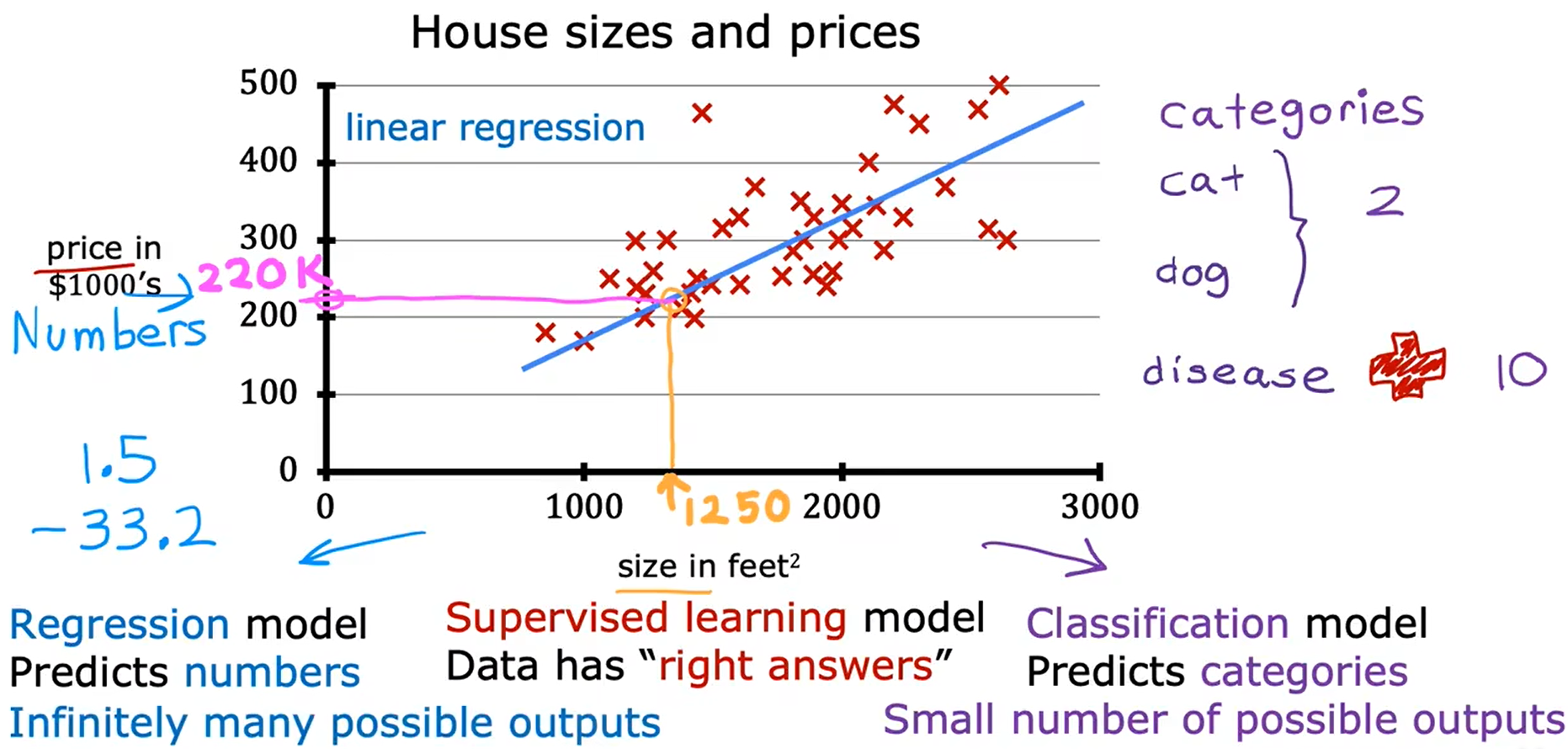
线性回归模型意味着对你的数据拟合一条直线,这可能是当今世界上使用最广泛的学习算法。它是一种特殊类型的监督学习模型,它被称为回归模型,因为它预测数字作为输出。
在回归模型中,模型可以输出无限多的可能数字,但分类模型只有少量可能的产出,所以有一个可能输出的离散有限集。
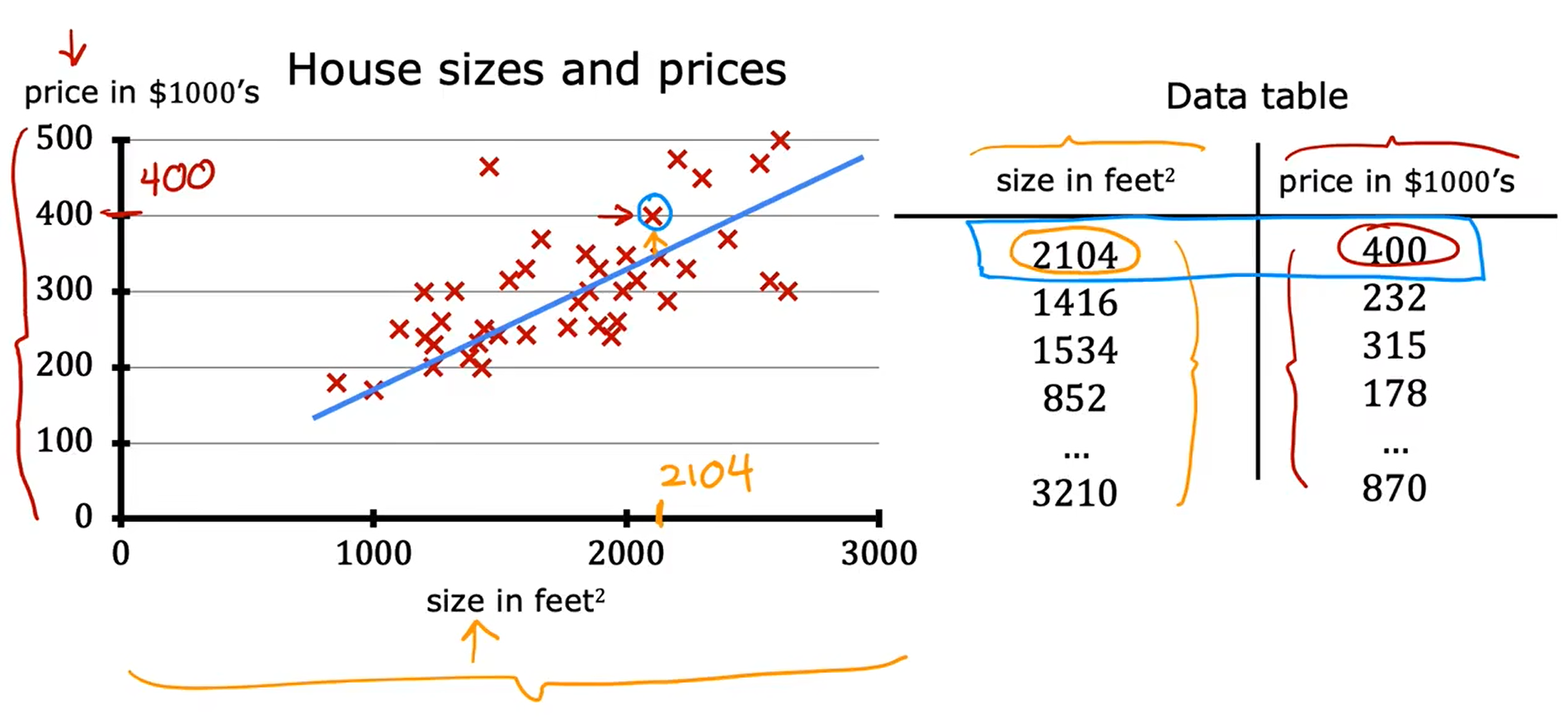
例如:根据房子的大小来预测房子的价格。
术语
- 用来训练模型的数据集叫作 训练集
- 输入变量也叫作特征或者 输入特征
- 输出变量(目标变量、输出目标)

训练集、输入特征、输出目标 →→→ 学习算法 →→→ 功能函数
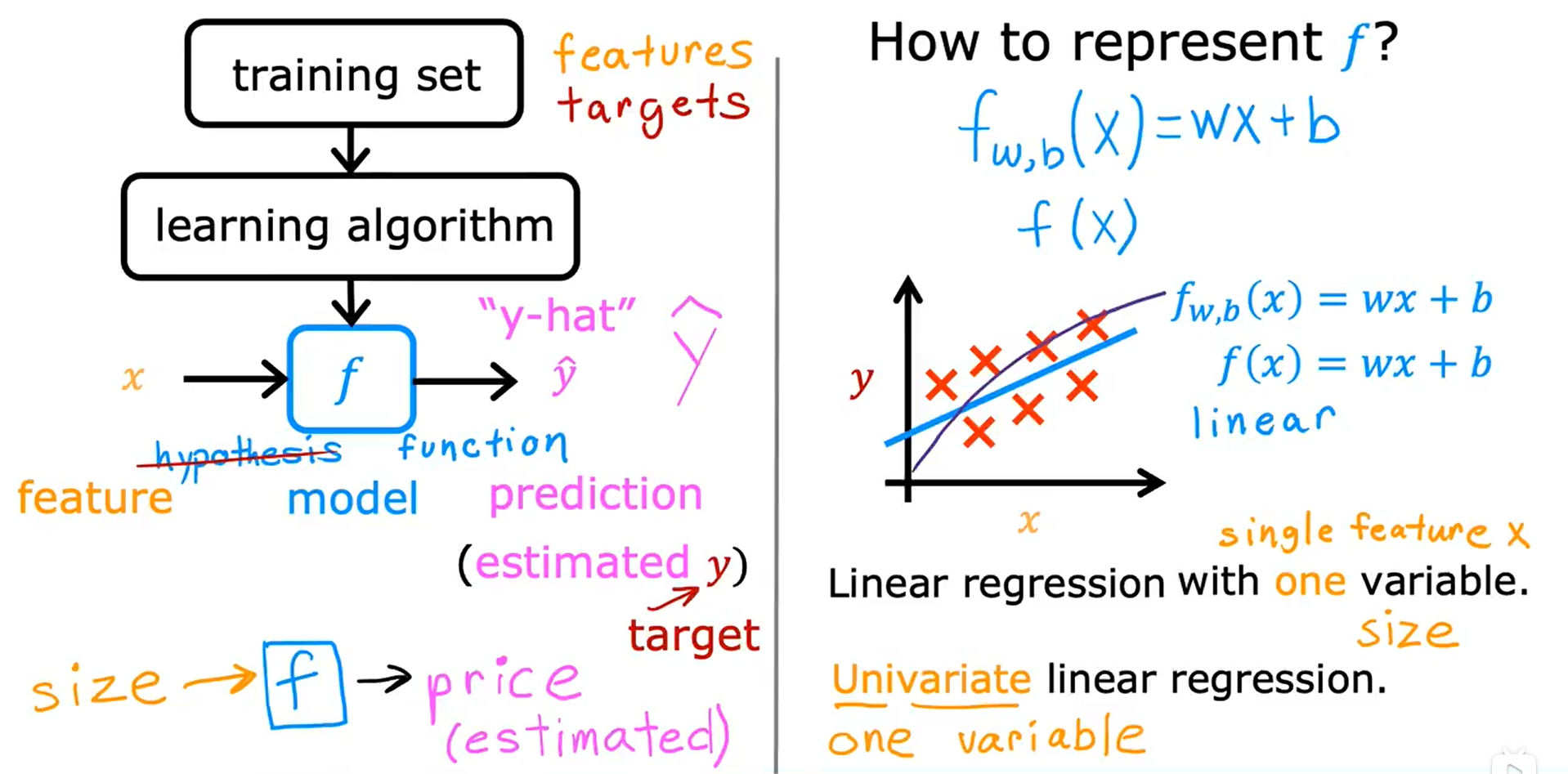
函数 f 称为模型。y是目标,是训练集中的实际真实值。y-hat 是对 y 的估计或预测,它可能是也可能不是实际的真实值。
线性函数只是直线的一个花哨术语,而不是曲线或抛物线等非线性函数。
线性回归,带有一个变量的线性回归,具有一个输入变量的线性模型又称 单变量线性回归。
成本(代价)函数 Cost Function
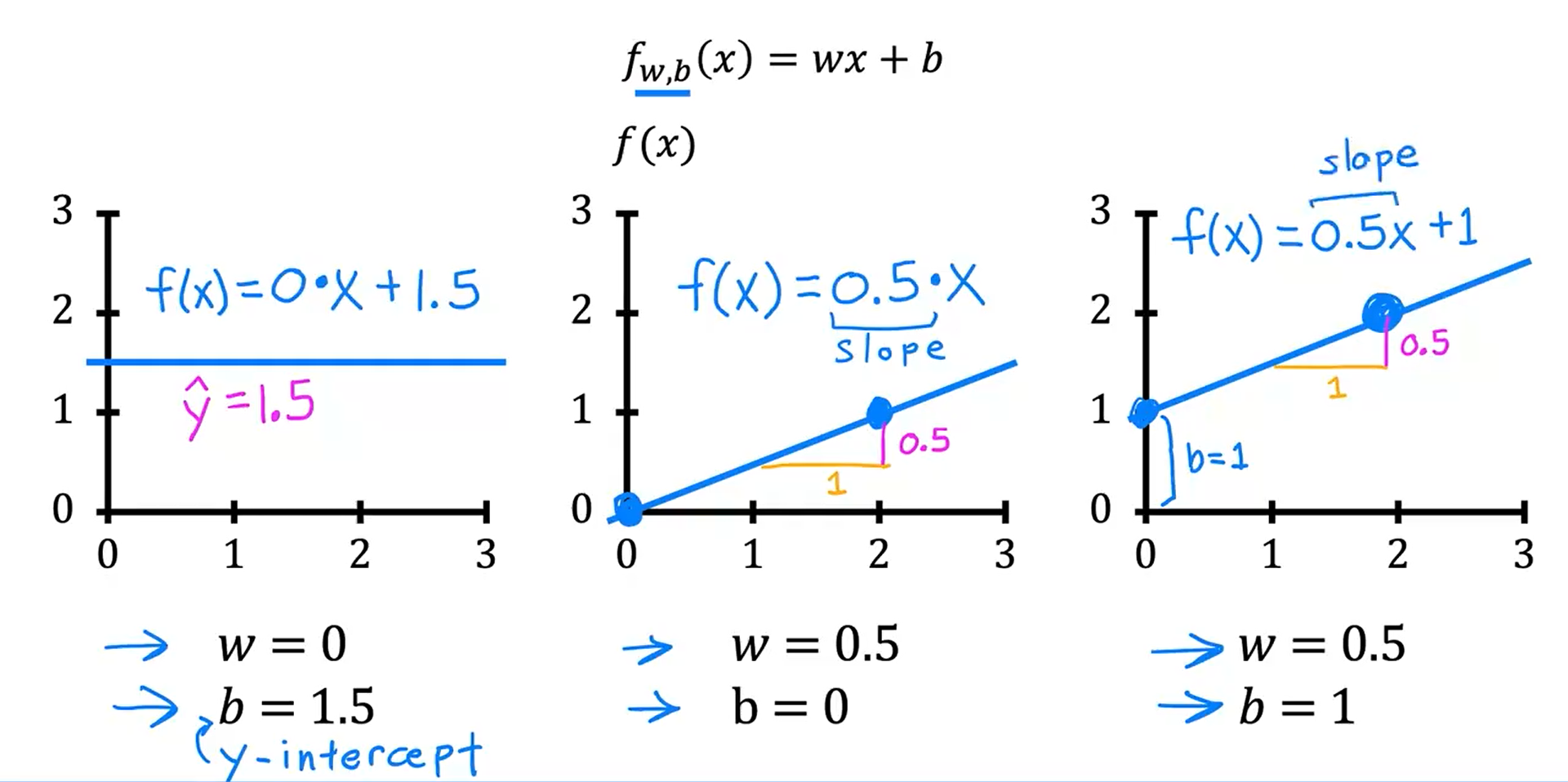
模型:f_w,b (x) = wx +b
在机器学习中,w 和 b 被称为模型的参数,模型的参数是可以在训练中调整的变量,以改进模型,在此例中,以便直线更好地拟合训练数据。有时 w 和 b 也被称为系数或权重。
机器学习使用的成本函数实际上是 m 的两倍,额外的除以 2 是为了让我们以后的一些计算更整洁一点。
此例中的成本函数也称为 平方误差成本函数,平方误差成本函数是线性回归中最常用的函数
为了衡量参数 w 和 b 的选择与训练数据的匹配程度(测量训练数据的对齐程度),所以使用代价函数J(w,b)

代价函数的直观理解
代价函数的作用是衡量模型的预测值与y的真实值之间的差异
线性回归的目标是找到参数 w (或参数 w 和 b),找到代价函数 J 的最小可能值
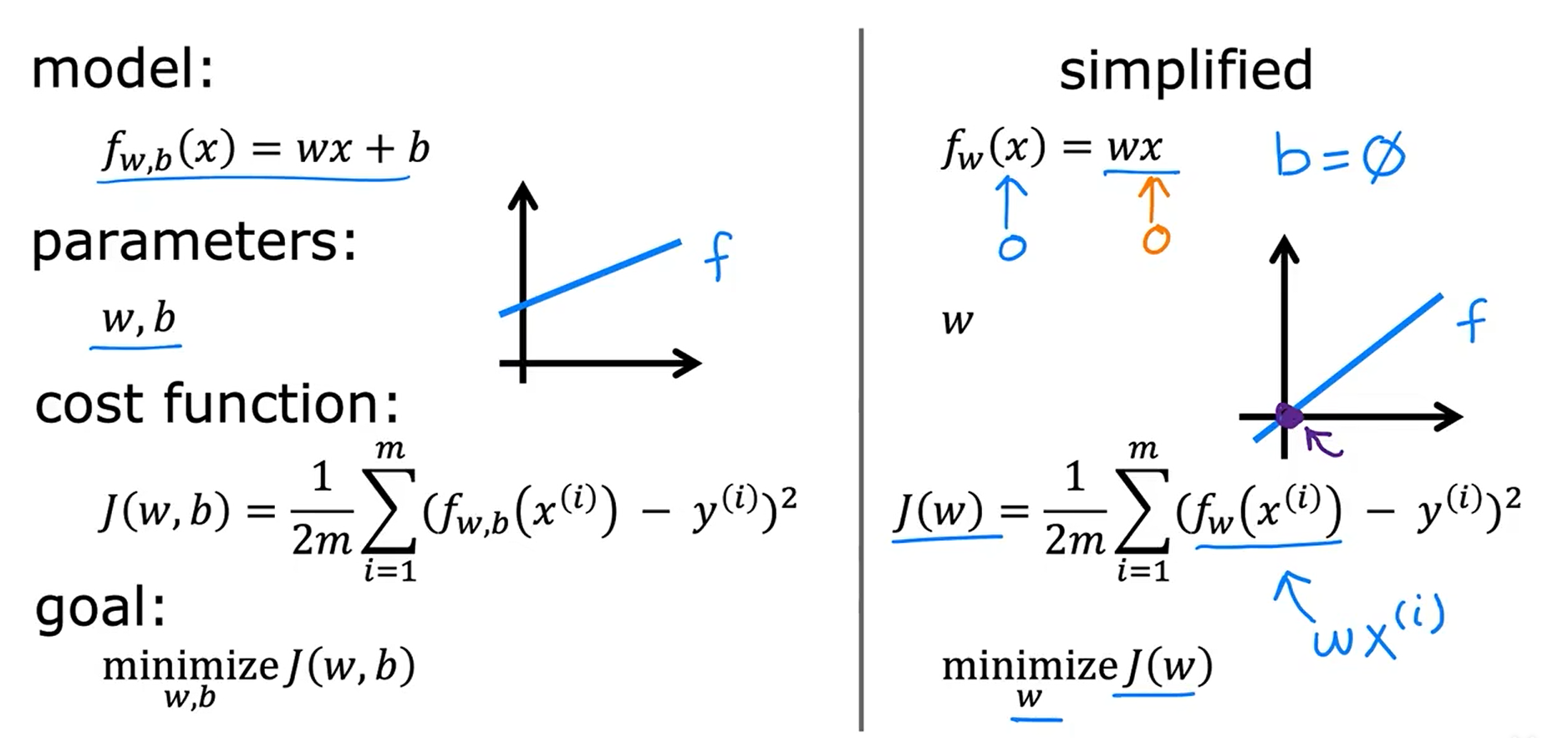
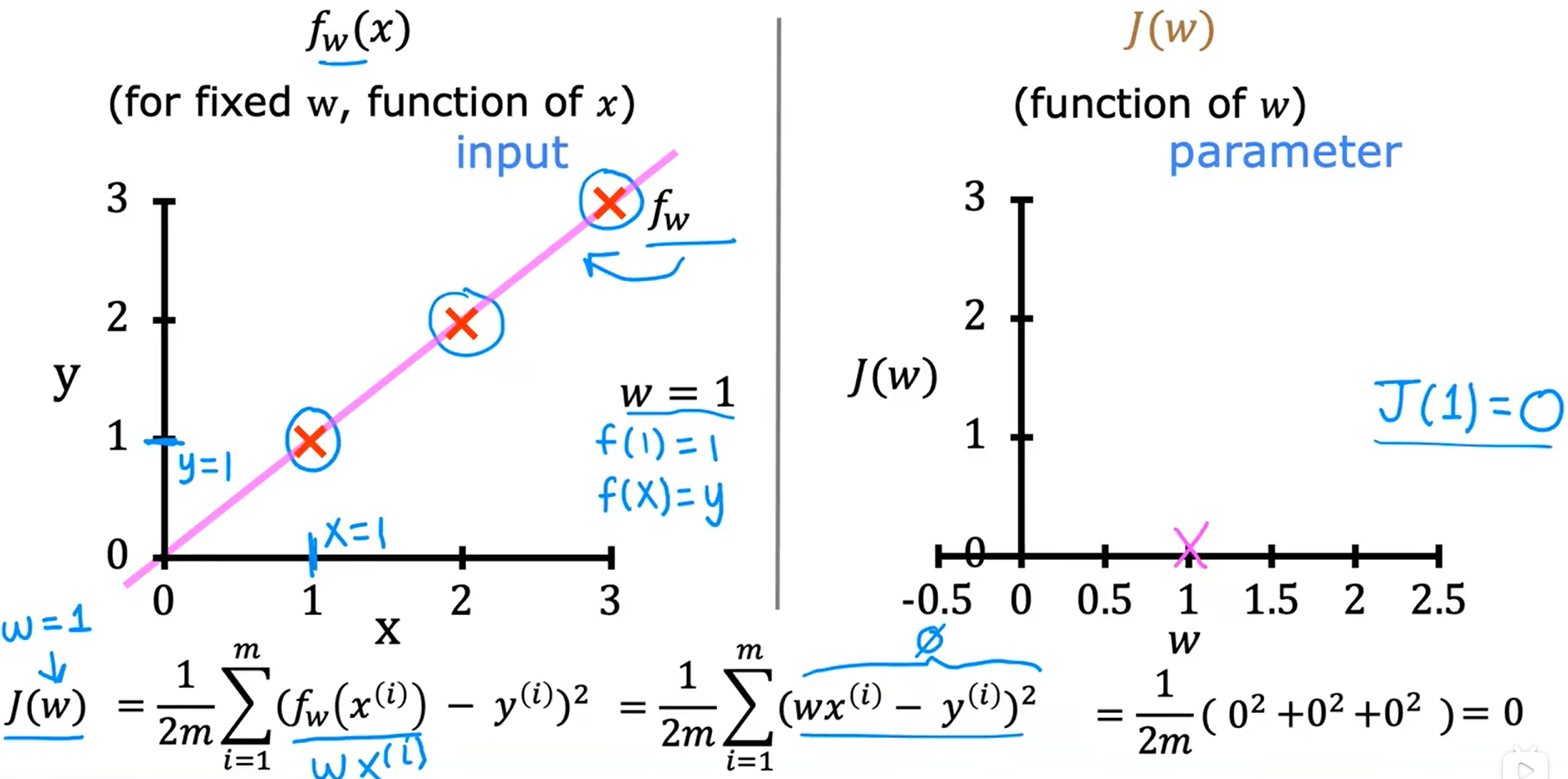
模型简化后的图像与代价函数图像的对比:
w = 1 ===> J(w) = 0
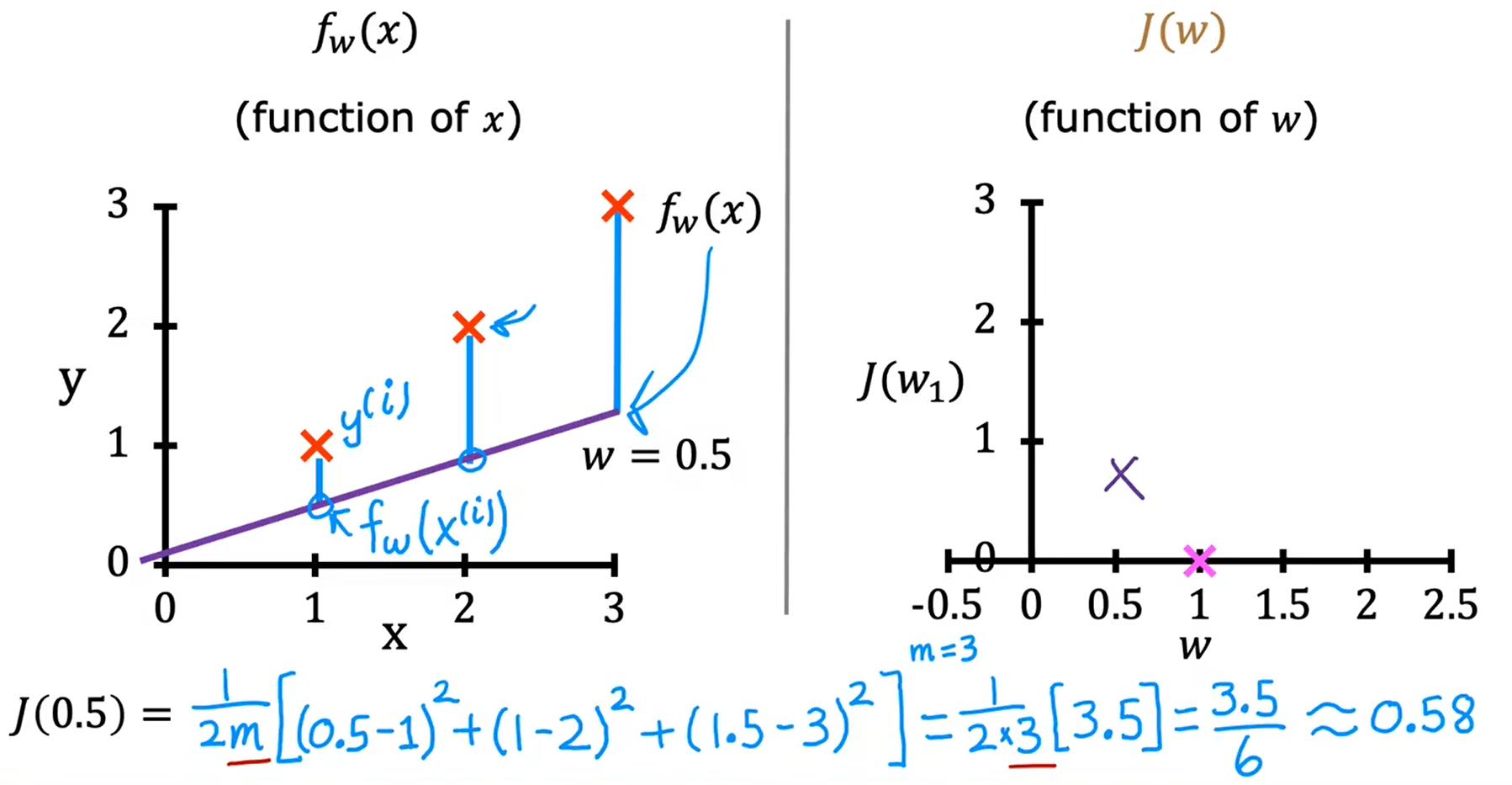
w = 0.5 ===> J(w) = 0.58
w = 0 ===> J(w) = 2.3
w = -0.5 ===> J(w) = 5.25
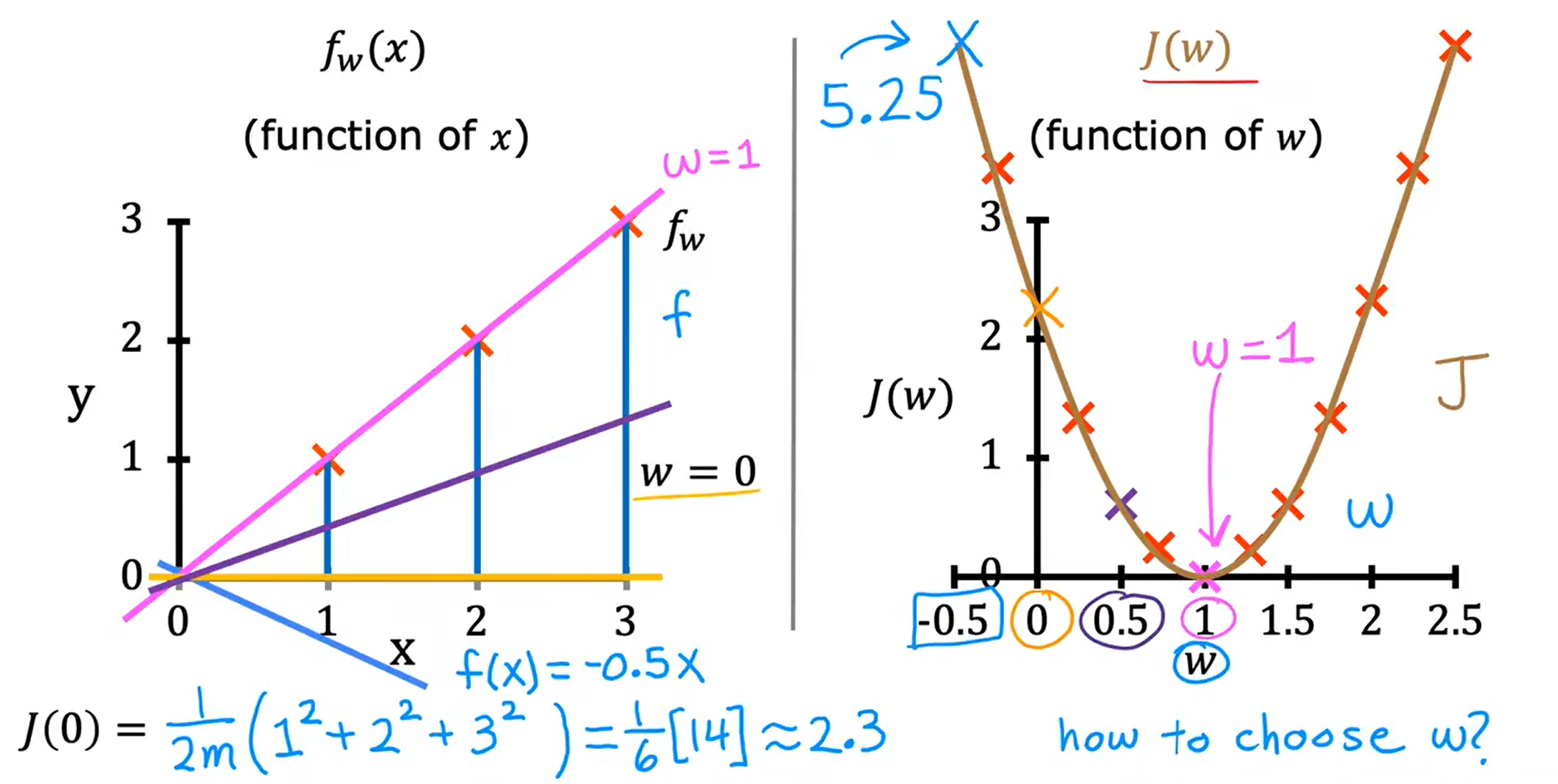
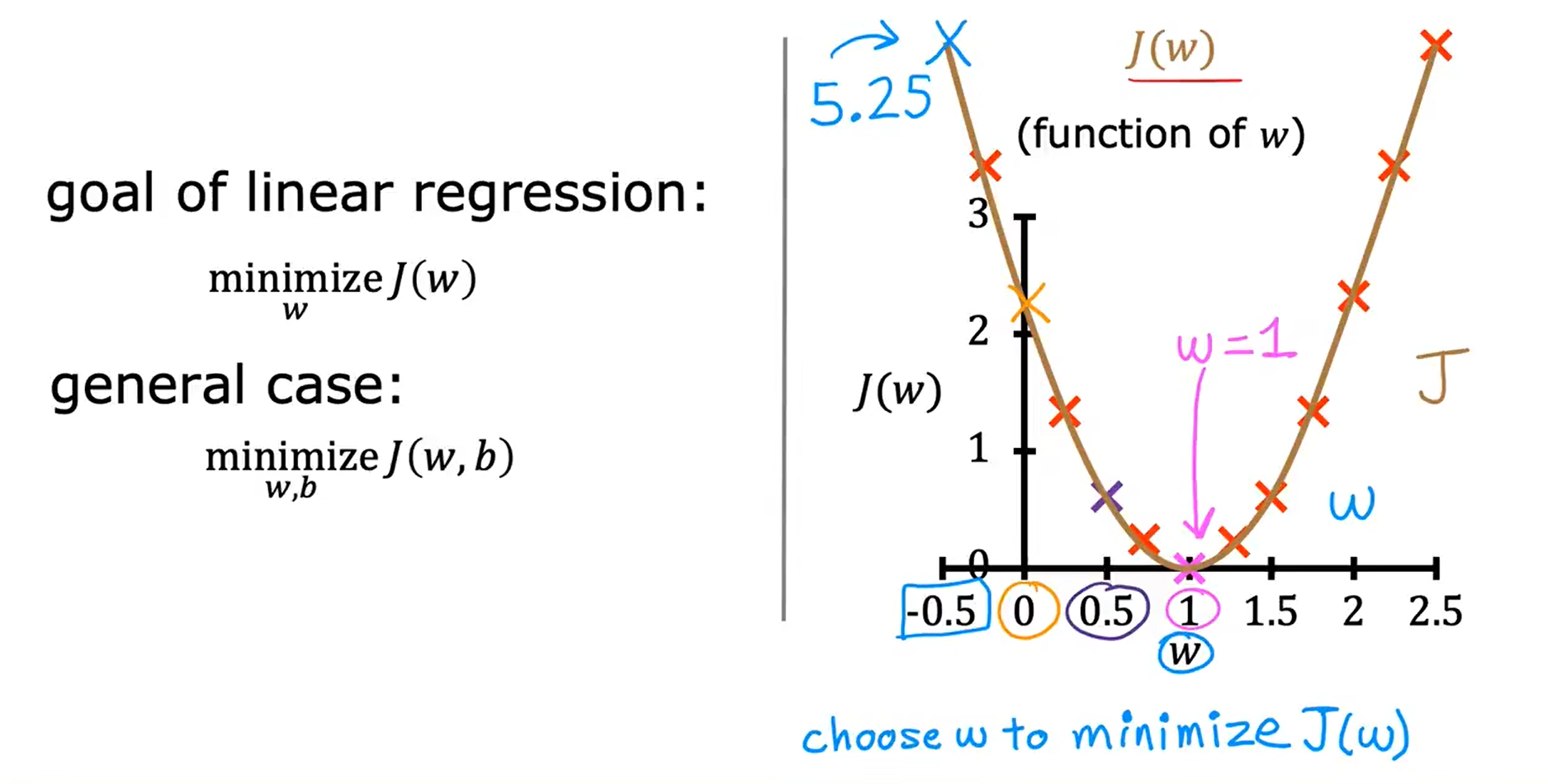
可视化代价函数
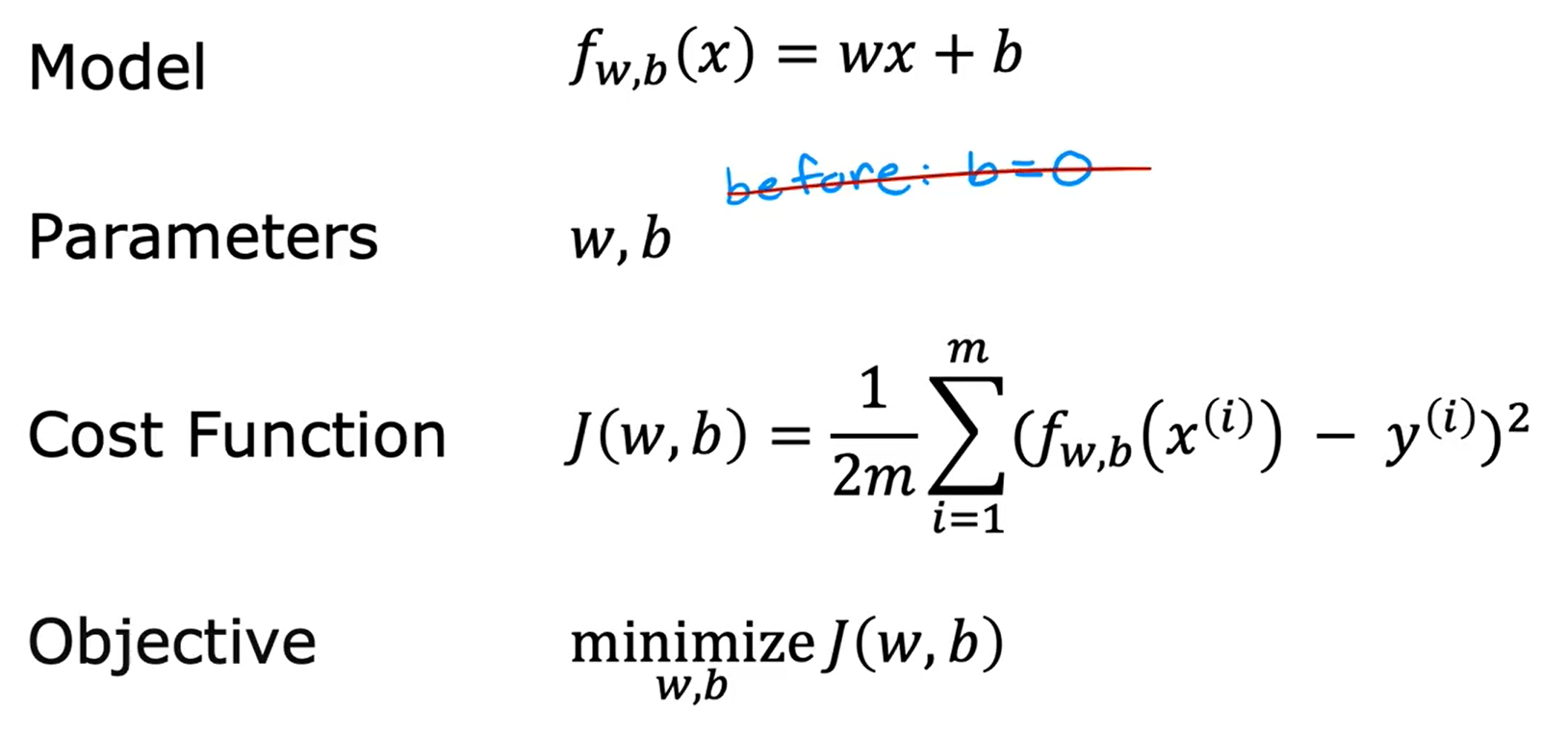
对下面这个尺寸预测房价的模型,忽略参数 b 的值,只考虑参数 w 得到的代价函数图像:
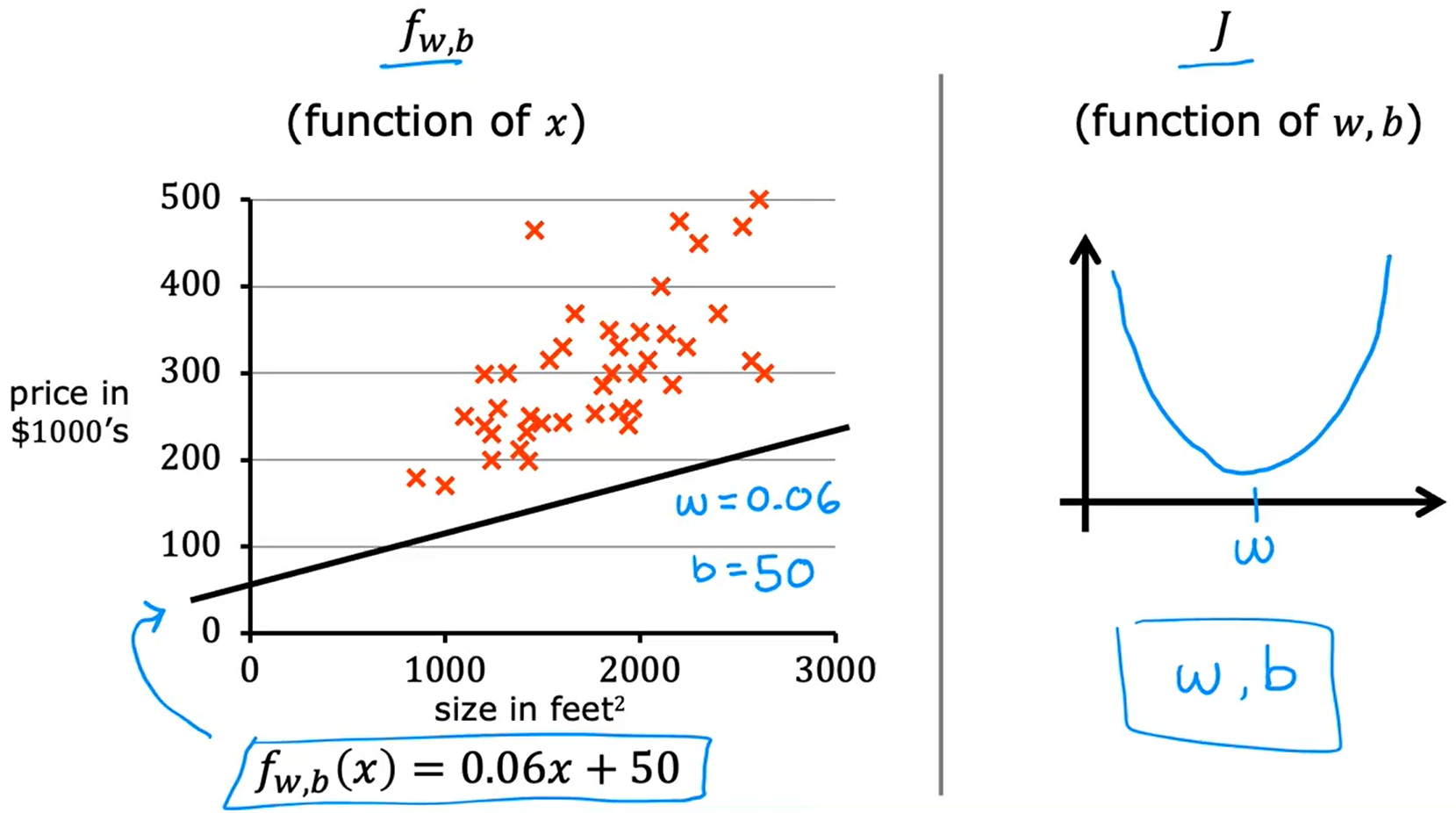
考虑参数 w 和 b 后得到的代价函数:
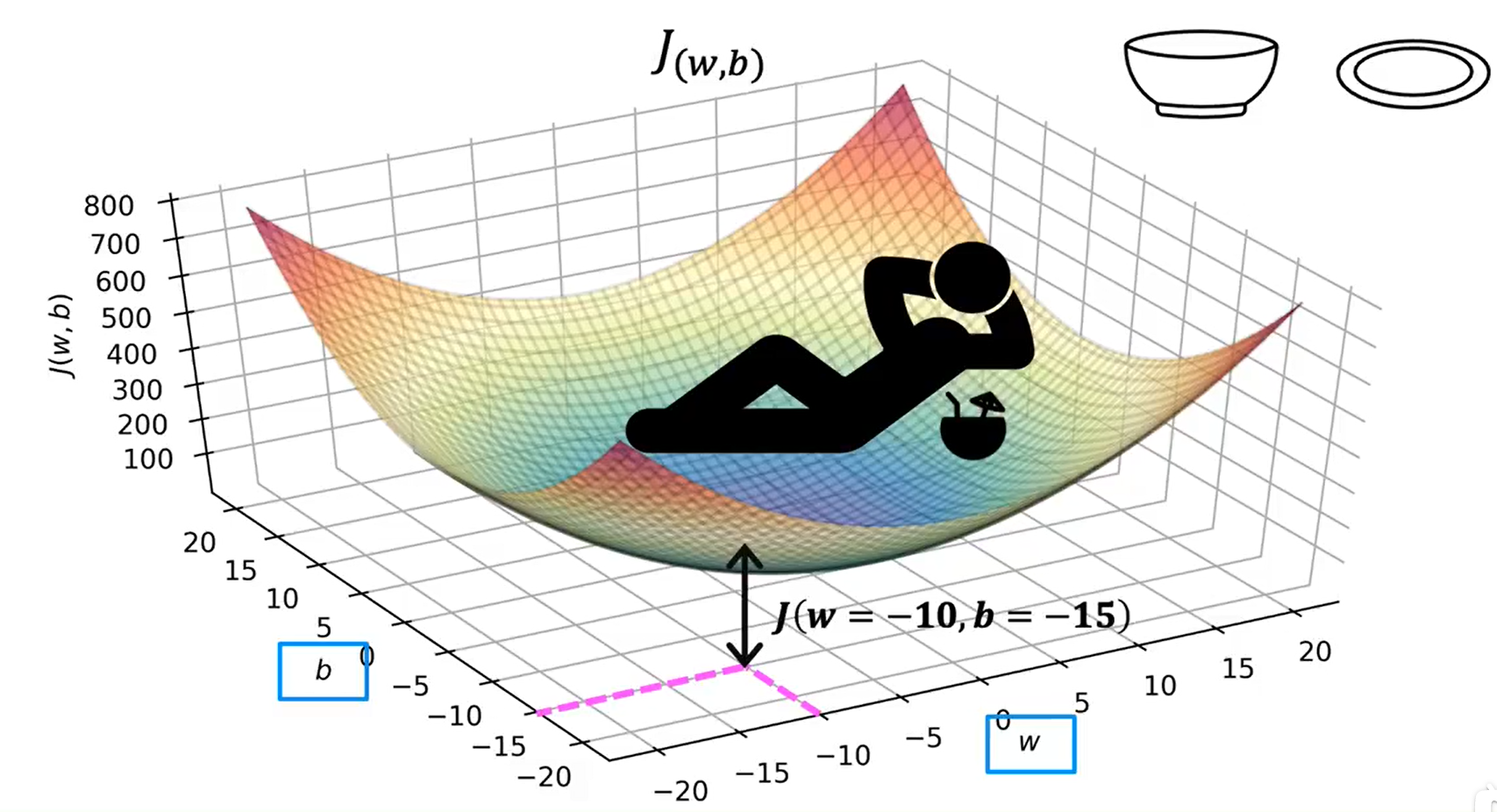
使用等高线图(右上角的图)来观察代价函数:
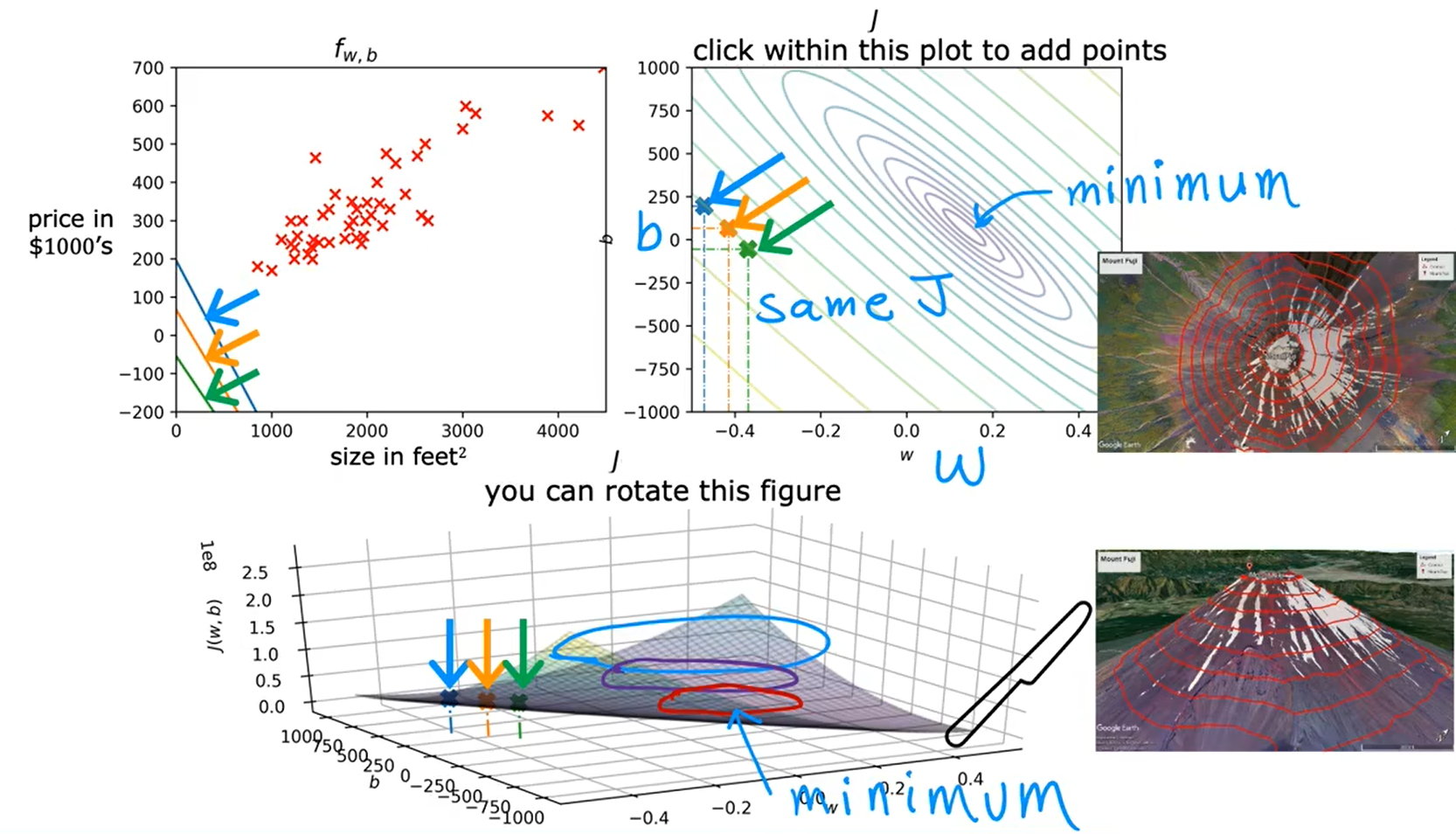
梯度下降 Gradient Descent
找到一个有效的算法,可以写在代码中自动查找参数 w 和 b 的值,它给你最适合的线,使成本函数最小化,梯度下降算法可以做到。
梯度下降在机器学习中无处不在,不仅用于线性回归,在人工智能中一些更大更复杂的模型也使用,比如训练一些最先进的神经网络模型,也被称为深度学习模型。
梯度下降是一种算法,可以用它来最小化任何函数,不仅仅是线性回归的成本函数。
- 一般先设置参数为0
- 然后逐步改变参数的值,来减少成本函数的值
- 直到我们达到或接近最小值(而且这个最低限度可能不止一个)

局部最小值
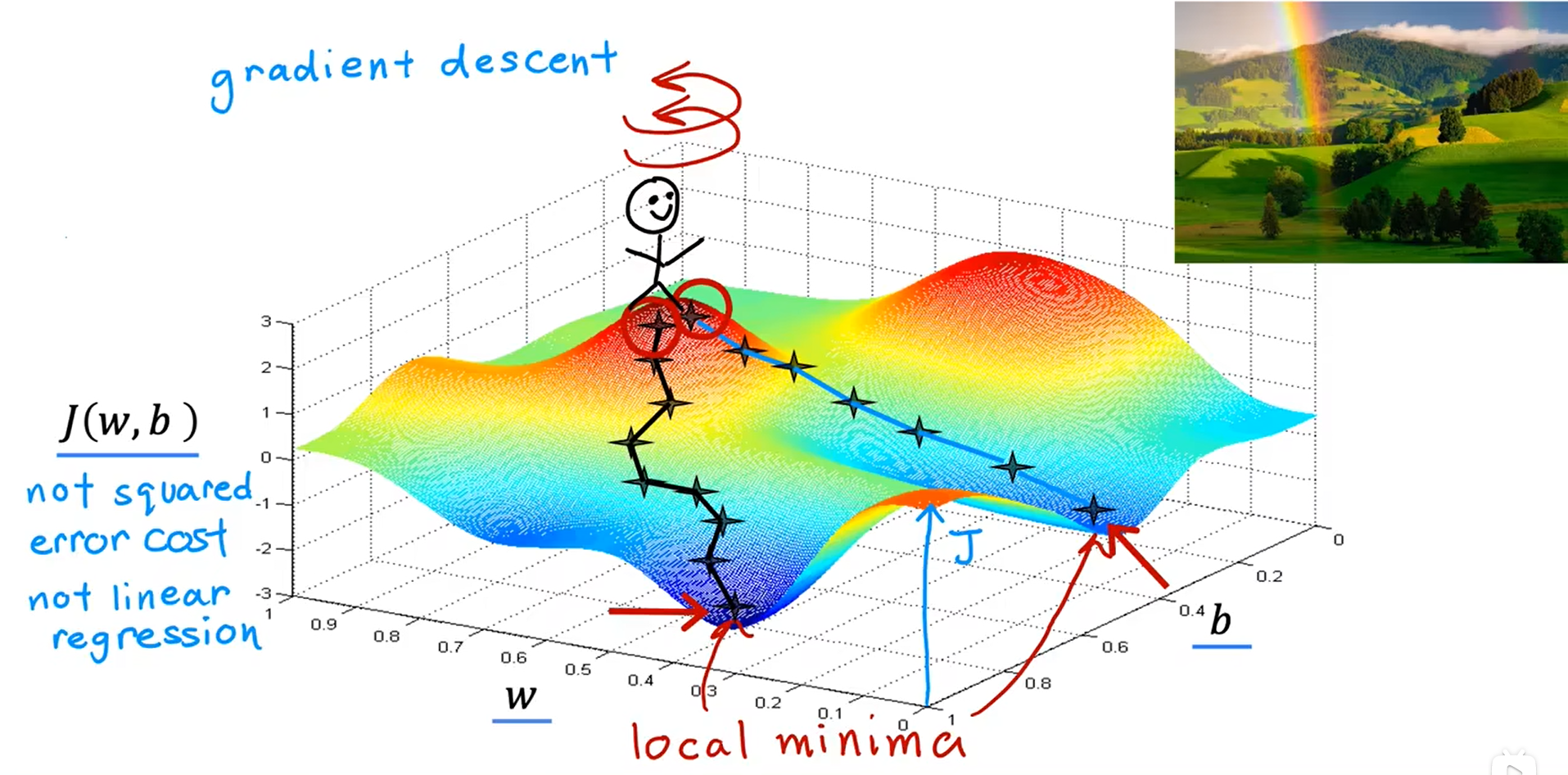
实现梯度下降
α:学习率(Learning Rate),学习率通常是0到1之间的一个数,比如0.1 0.2;这个变量控制下坡时的步幅,在这个例子中即是更行模型参数 w 和 b 时迈出的步子的大小。
∂J(w, b) / ∂w:成本函数的(偏)导数项,下坡时的方向
更新参数 w 和 b的值,然后不断重复这两个步骤,直到算法收敛,然后达到一个局部最小值。在这个最小值下,参数 w 和 b 不再随着采取的每一个额外步骤而变化很大。
通过 同步更新 以正确的方式实现它更自然,左下角的步骤是正确的,求 tmp_b 时带入的w的值是旧值,而不是 tmp_w 的值。

梯度下降的直观理解

从点 w 左侧,斜率为负数,所以从左向右移动,新的w的值会增加;相反的,点w 右侧的斜率为整数,所以从右向左移动,新的w的值会减少。
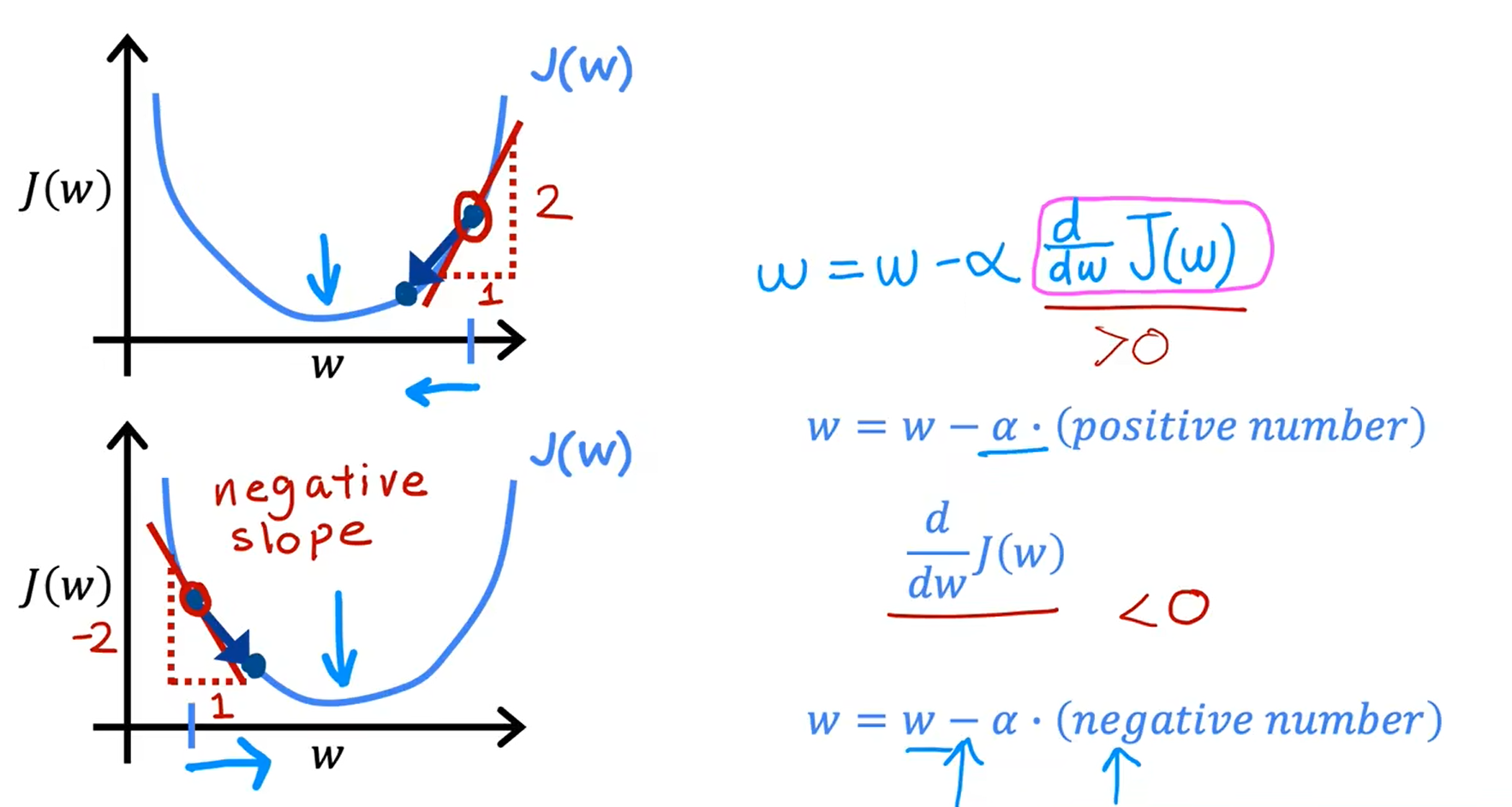
学习率 Learning Rate, α
- 如果学习率很小,那么梯度下降的速度会很慢,这会消耗很多的时间,因为在它接近最小值之前,它需要很多步骤,而且每一步的步幅都很小。
- 如果学习率过大,那么梯度下降可能会超过预期目标,可能永远都达不到最小(梯度下降可能无法收敛,甚至可能发散)。
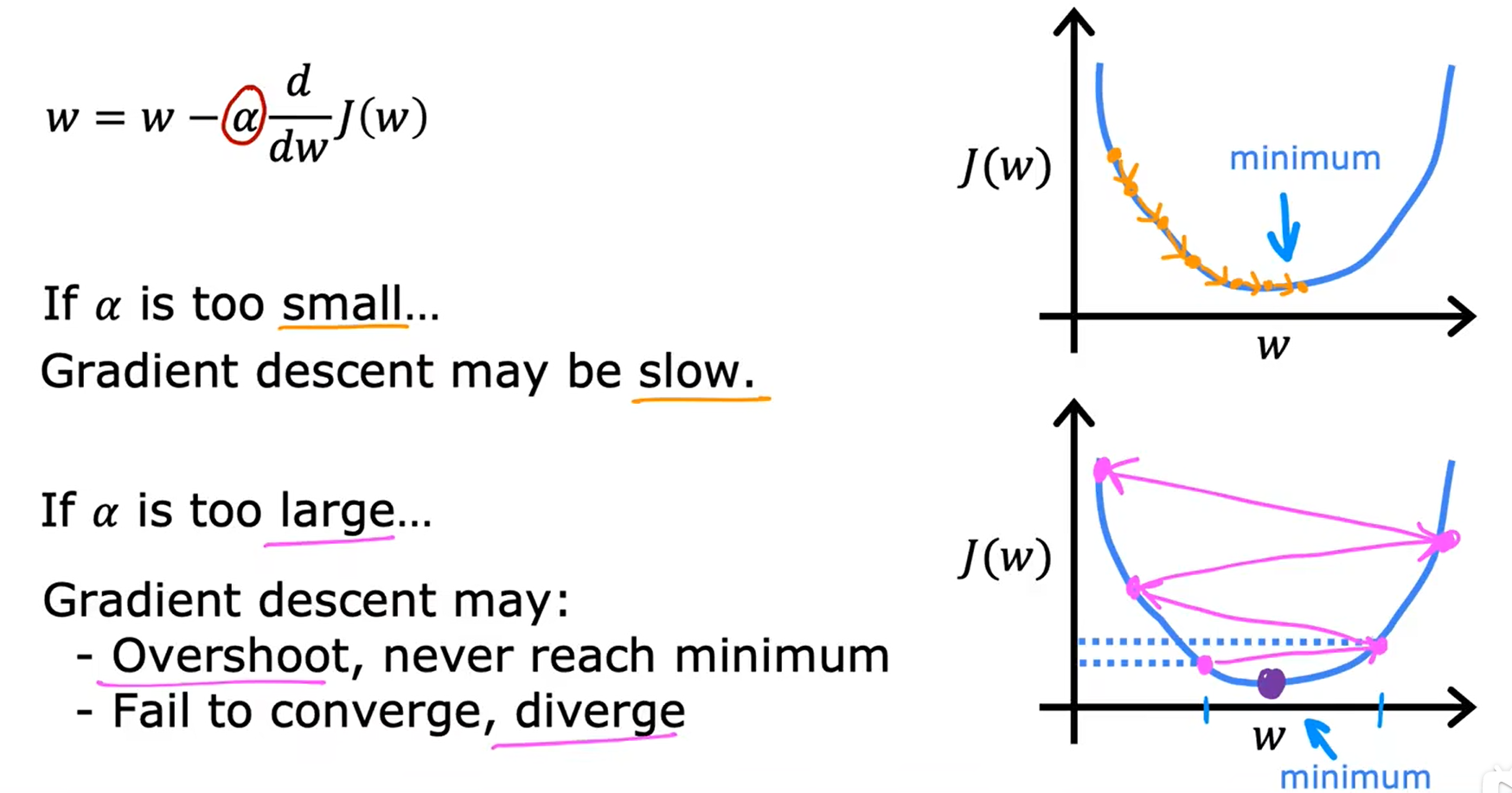
梯度下降可以达到局部最小值
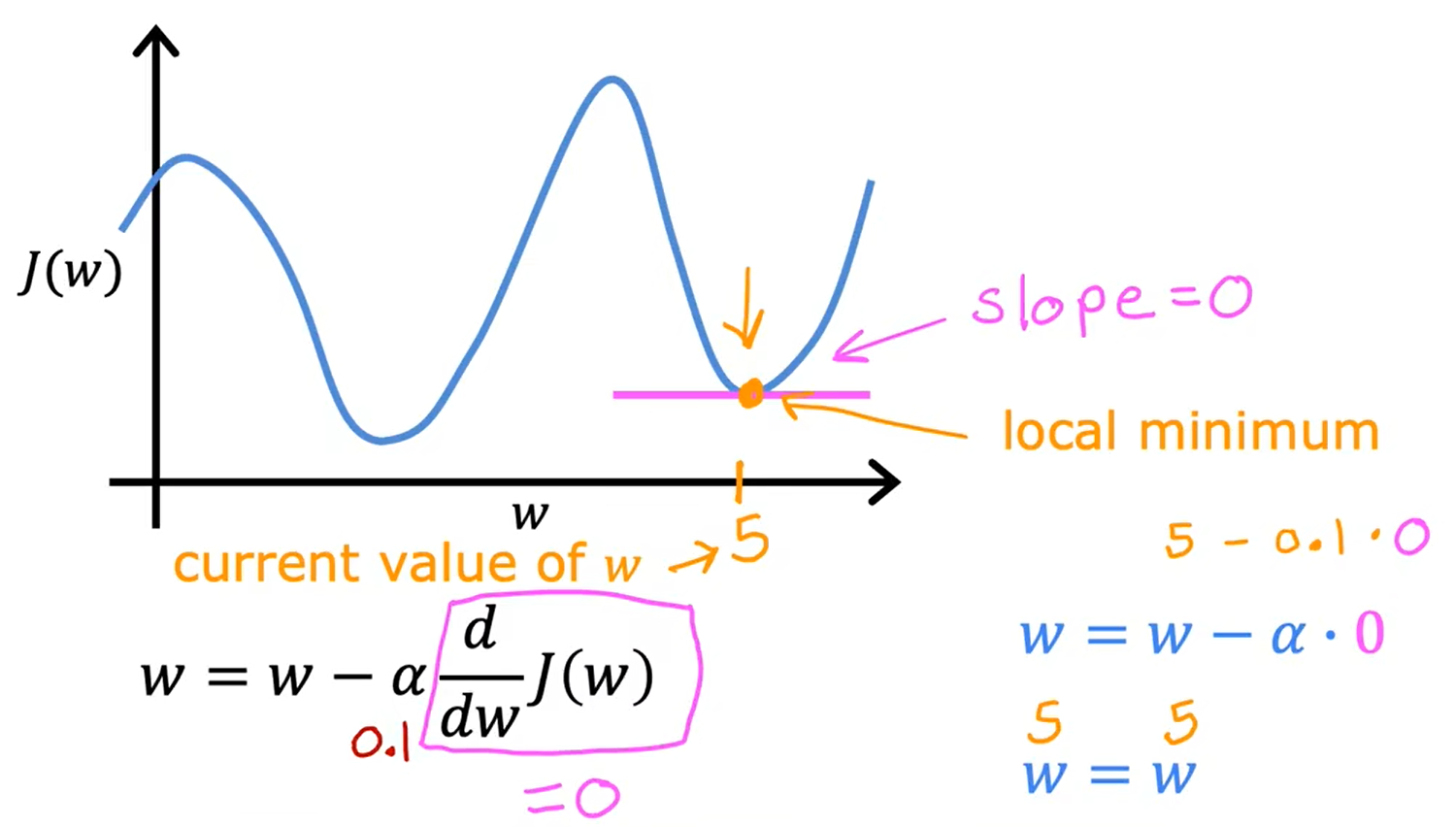
当接近局部最小值时,梯度下降将自动采取较小的步幅,因为当接近局部最小值时,导数会自动变小,这意味着更新步幅也会自动变小,即使学习率α保持在某个固定值。
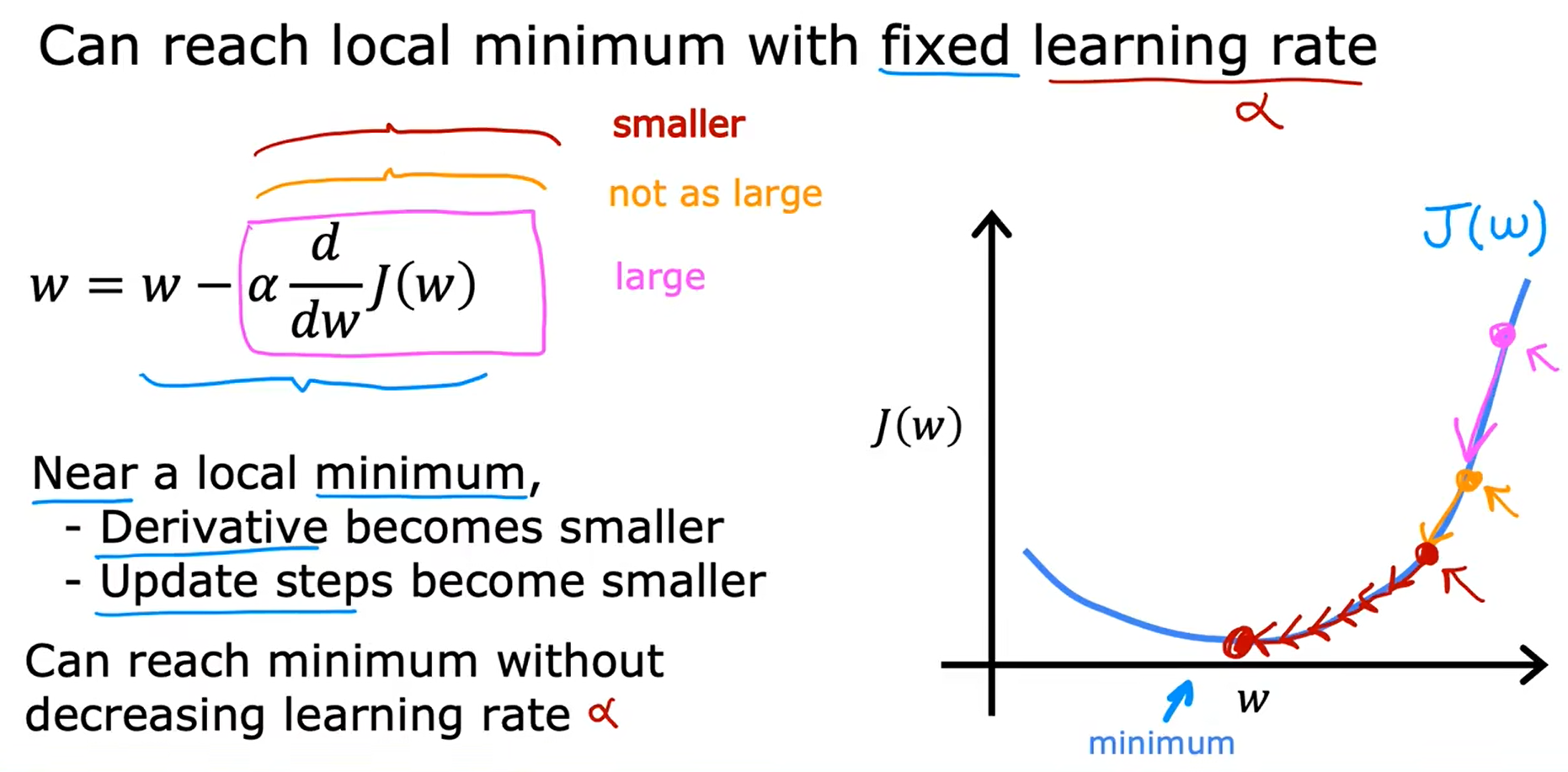
线性回归中的梯度下降
用平方误差成本函数来表示带有梯度下降的线性回归模型,将会训练线性回归模型,使其与我们的训练集数据符合成一条直线。

两个偏导数对应的公式的推导过程:
∂
∂
w
J
(
w
,
b
)
=
∂
∂
w
1
2
m
∑
i
=
1
m
(
f
w
,
b
(
x
(
i
)
)
−
y
(
i
)
)
2
=
∂
∂
w
1
2
m
∑
i
=
1
m
(
w
x
(
i
)
+
b
−
y
(
i
)
)
2
=
1
2
m
∑
i
=
1
m
(
w
x
(
i
)
+
b
−
y
(
i
)
)
2
x
(
i
)
=
1
m
∑
i
=
1
m
(
f
w
,
b
(
x
(
i
)
)
−
y
(
i
)
)
x
(
i
)
\frac{∂}{∂w} J(w, b) = \frac{∂}{∂w} \frac{1}{2m} \sum_{i=1}^m (f_{w, b}(x^{(i)}) - y^{(i)}) ^2 = \\ \frac{∂}{∂w} \frac{1}{2m} \sum_{i=1}^m (wx^{(i)} + b - y^{(i)}) ^2 = \\ \frac{1}{2m} \sum_{i=1}^m (wx^{(i)} + b - y^{(i)}) 2x^{(i)} = \\ \frac{1}{m} \sum_{i=1}^m (f_{w, b}(x^{(i)}) - y^{(i)}) x^{(i)}
∂w∂J(w,b)=∂w∂2m1i=1∑m(fw,b(x(i))−y(i))2=∂w∂2m1i=1∑m(wx(i)+b−y(i))2=2m1i=1∑m(wx(i)+b−y(i))2x(i)=m1i=1∑m(fw,b(x(i))−y(i))x(i)
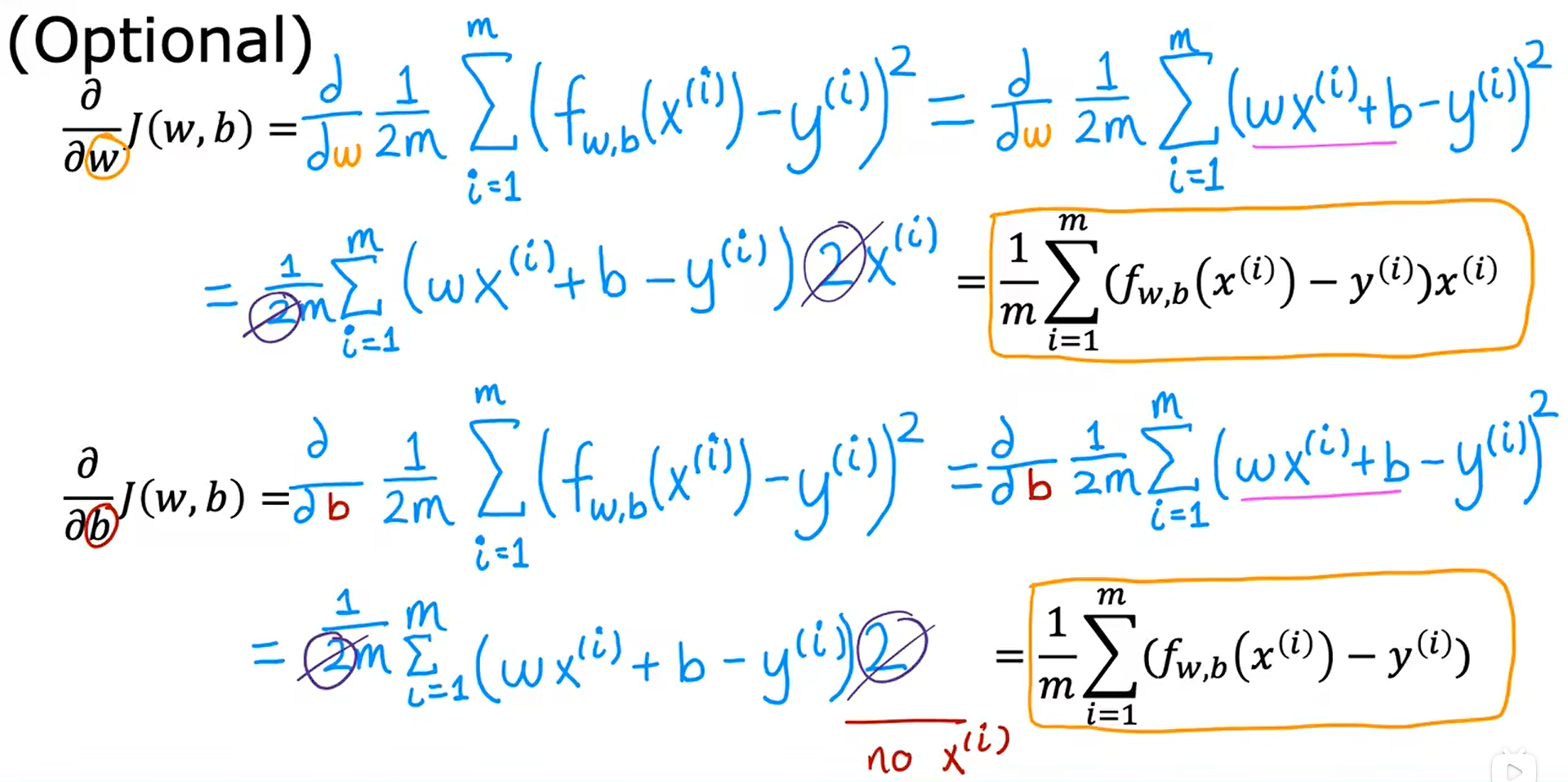
最终的梯度下降算法:

这个模型的成本函数有多个局部最小值,而且可以在不同的局部最小值结束运算。
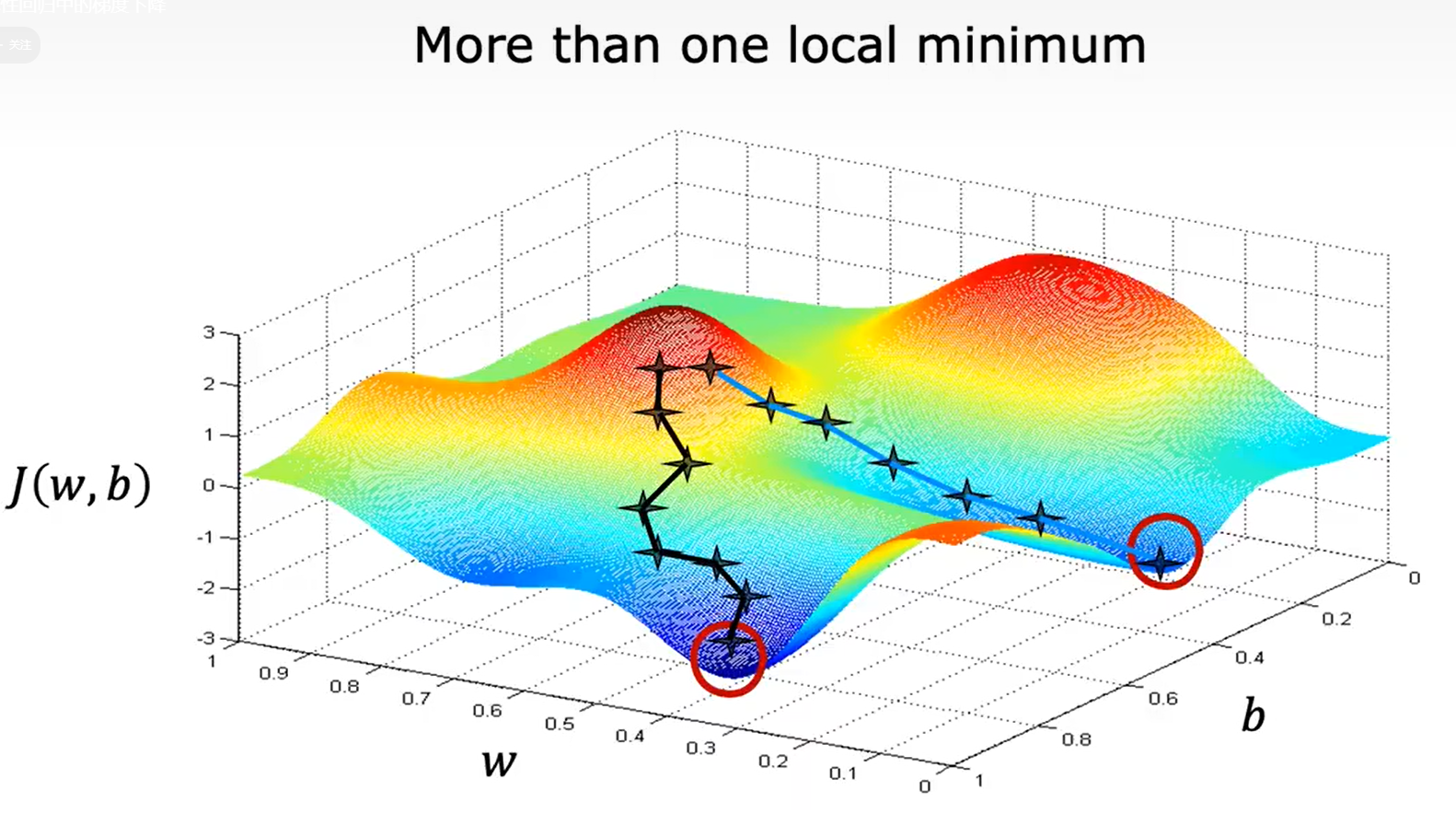
但当使用线性回归模型的平方误差成本函数时,成本函数不会有多个局部最小值,只有一个单一的全局最小值。且此时的成本函数为凸函数。
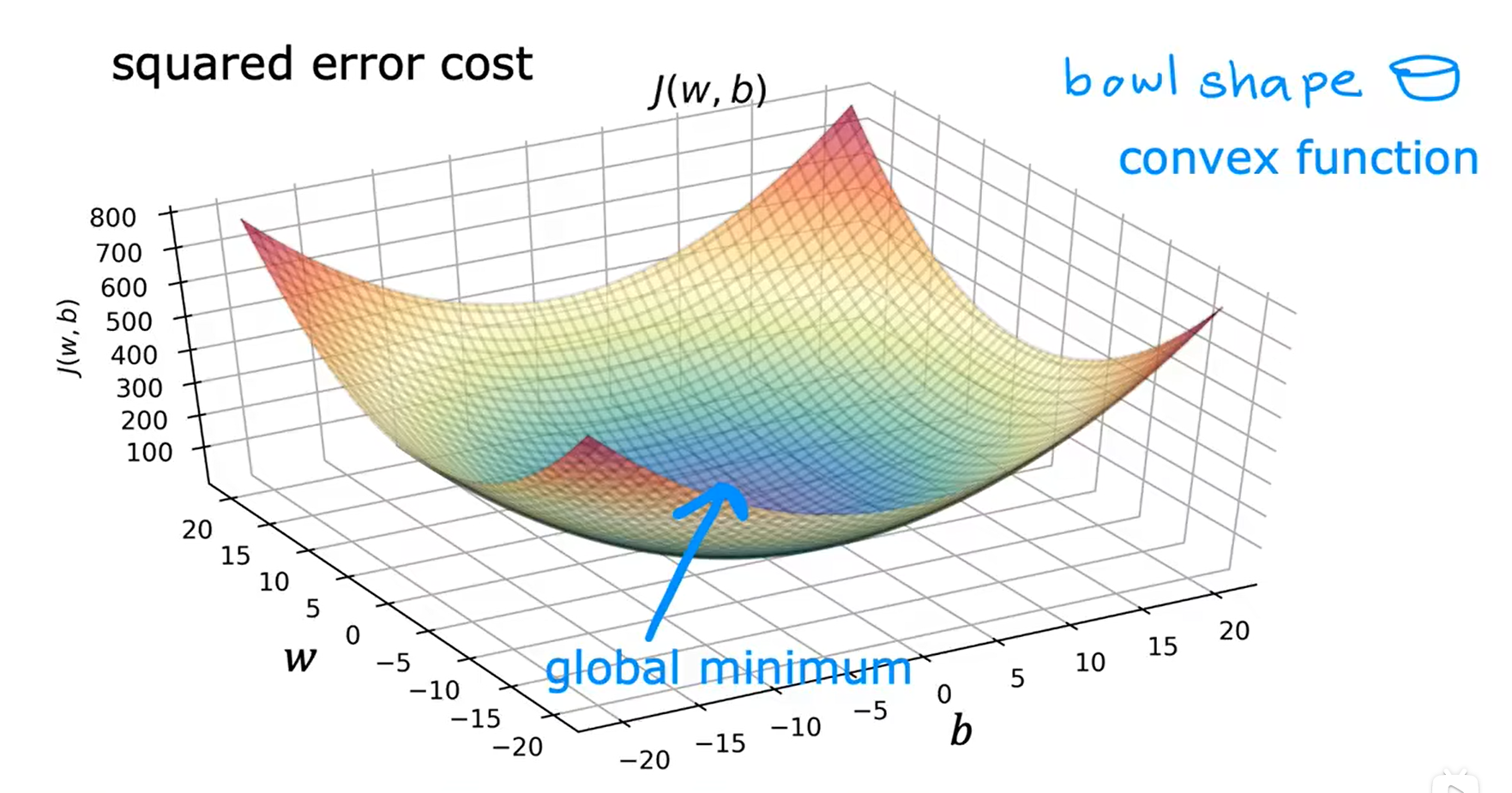
运行梯度下降
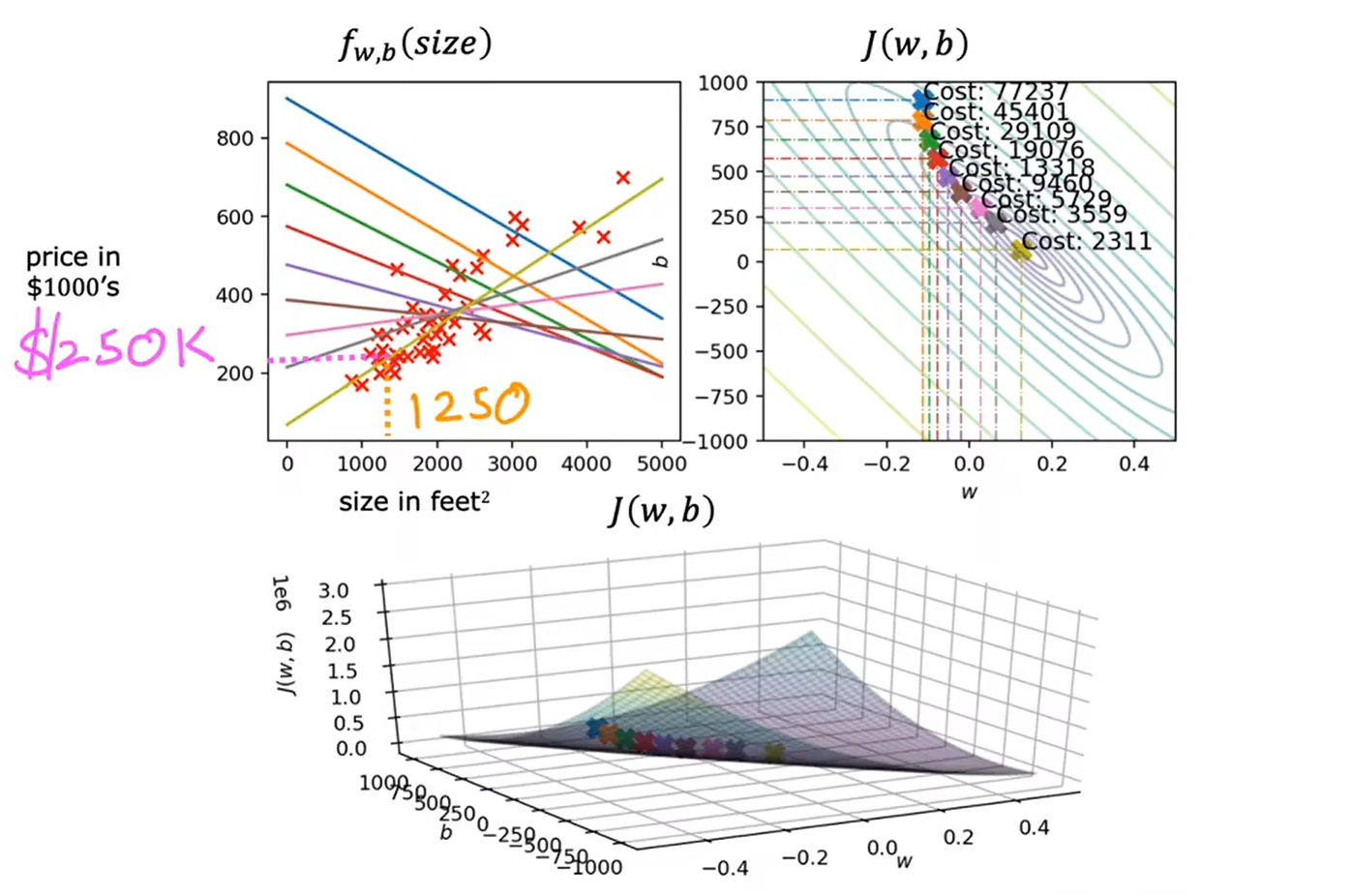
间歇梯度下降
在梯度下降的每一个步骤上,我们所看到的是所有的训练示例,而仅仅是训练数据的子集。
多种特征 Multiple Features
多元线性回归
多类特征是指有多个特征值。以预测房价为例,在前面的线性回归模型,其中只有一个特征w, 它是房子的面积。但是我们在实际预测价格的时候,使用一个特征可能预测的并不会很准。所以现在不光是通过房屋面积来预测房价,并加入卧室数量、楼层数、房屋年龄 这些特征(变量)来计算房价,这些都可以作为特征值。
x
j
:
第
j
列,即第
j
个特征
n
:特征的数量
x
⃗
(
i
)
:
第
i
个训练样本,即第
i
行数据
x
j
(
i
)
:
第
i
个训练样本的第
j
个特征的值
x_j : 第 j 列,即第 j 个特征 \\ n:特征的数量 \\ \vec{x}^{(i)} : 第 i 个训练样本,即第 i 行数据 \\ x^{(i)}_j : 第 i 个训练样本的 第 j 个特征的值 \\
xj:第j列,即第j个特征n:特征的数量x(i):第i个训练样本,即第i行数据xj(i):第i个训练样本的第j个特征的值
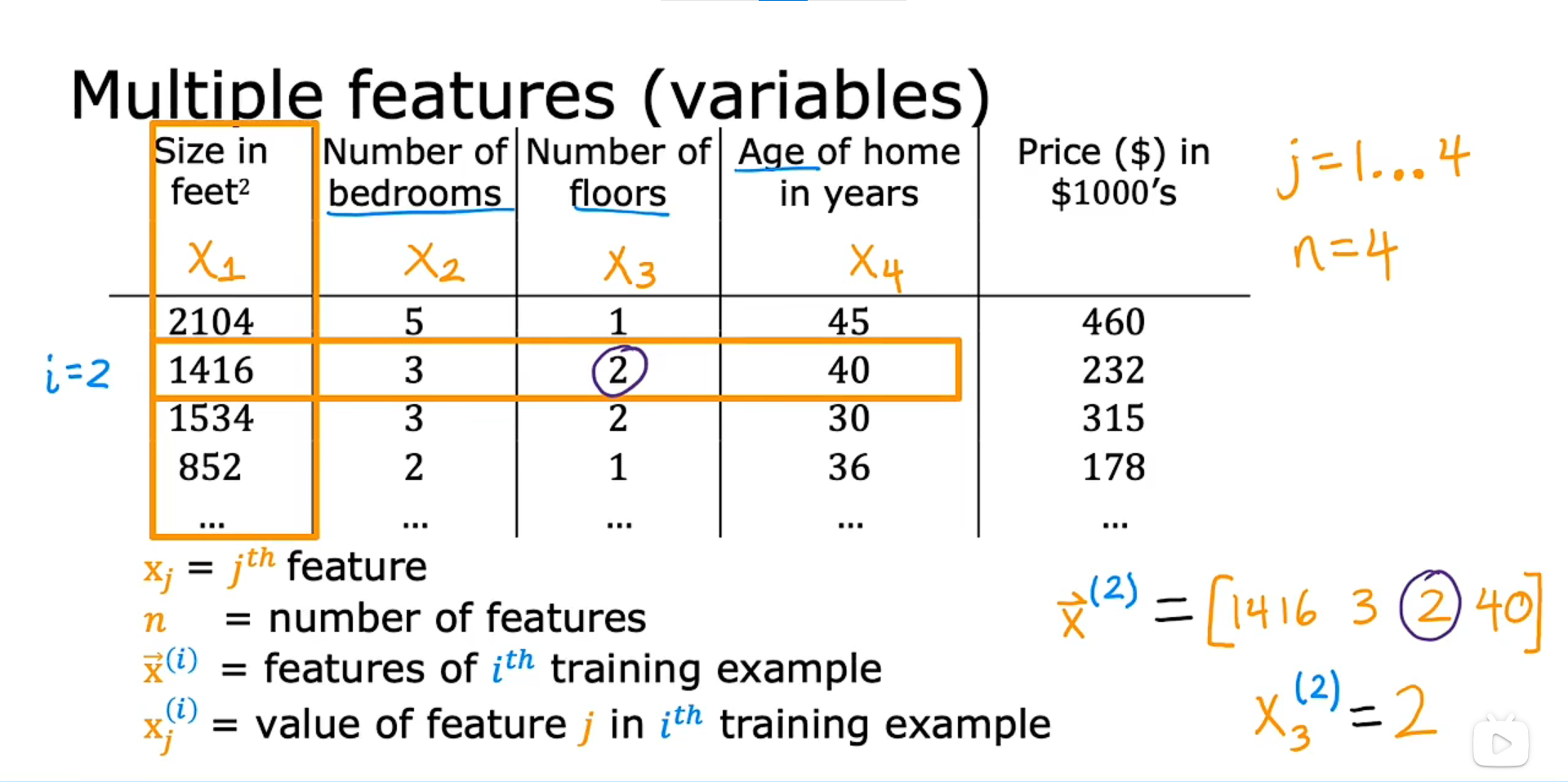
带有多个特征的模型的定义:
M
o
d
e
l
:
Model:
Model:
P
r
e
v
i
o
u
s
l
y
:
f
w
,
b
(
x
)
=
w
x
+
b
Previously: f_{w, b}(x) = wx + b
Previously:fw,b(x)=wx+b
f
w
,
b
(
x
)
=
w
1
x
1
+
w
2
x
2
+
w
3
x
3
+
w
4
x
4
+
b
f_{w, b}(x) = w_1x_1 + w_2x_2 + w_3x_3 + w_4x_4 + b
fw,b(x)=w1x1+w2x2+w3x3+w4x4+b
e
x
a
m
p
l
e
:
f
w
,
b
(
x
)
=
0.1
x
1
+
4
x
2
+
10
x
3
+
(
−
2
)
x
4
+
80
example: f_{w,b}(x) = 0.1x_1 + 4x_2 + 10x_3 + (-2)x_4 + 80
example:fw,b(x)=0.1x1+4x2+10x3+(−2)x4+80
x
1
:
s
i
z
e
,
x
2
:
b
e
d
r
o
o
m
s
,
x
3
:
f
l
o
o
r
s
,
x
4
:
y
e
a
r
s
,
80
:
b
a
s
e
p
r
i
c
e
x_1: size, x_2: bedrooms, x_3: floors, x_4: years, 80: base price
x1:size,x2:bedrooms,x3:floors,x4:years,80:baseprice
f
w
,
b
(
x
)
=
w
1
x
1
+
w
2
x
2
+
⋅
⋅
⋅
+
w
n
x
n
+
b
f_{w, b}(x) = w_1x_1 + w_2x_2 + ··· + w_nx_n + b
fw,b(x)=w1x1+w2x2+⋅⋅⋅+wnxn+b
具有多种改进特征的模型是 多元(特征)线性回归 :
向量化 矢量化 点积
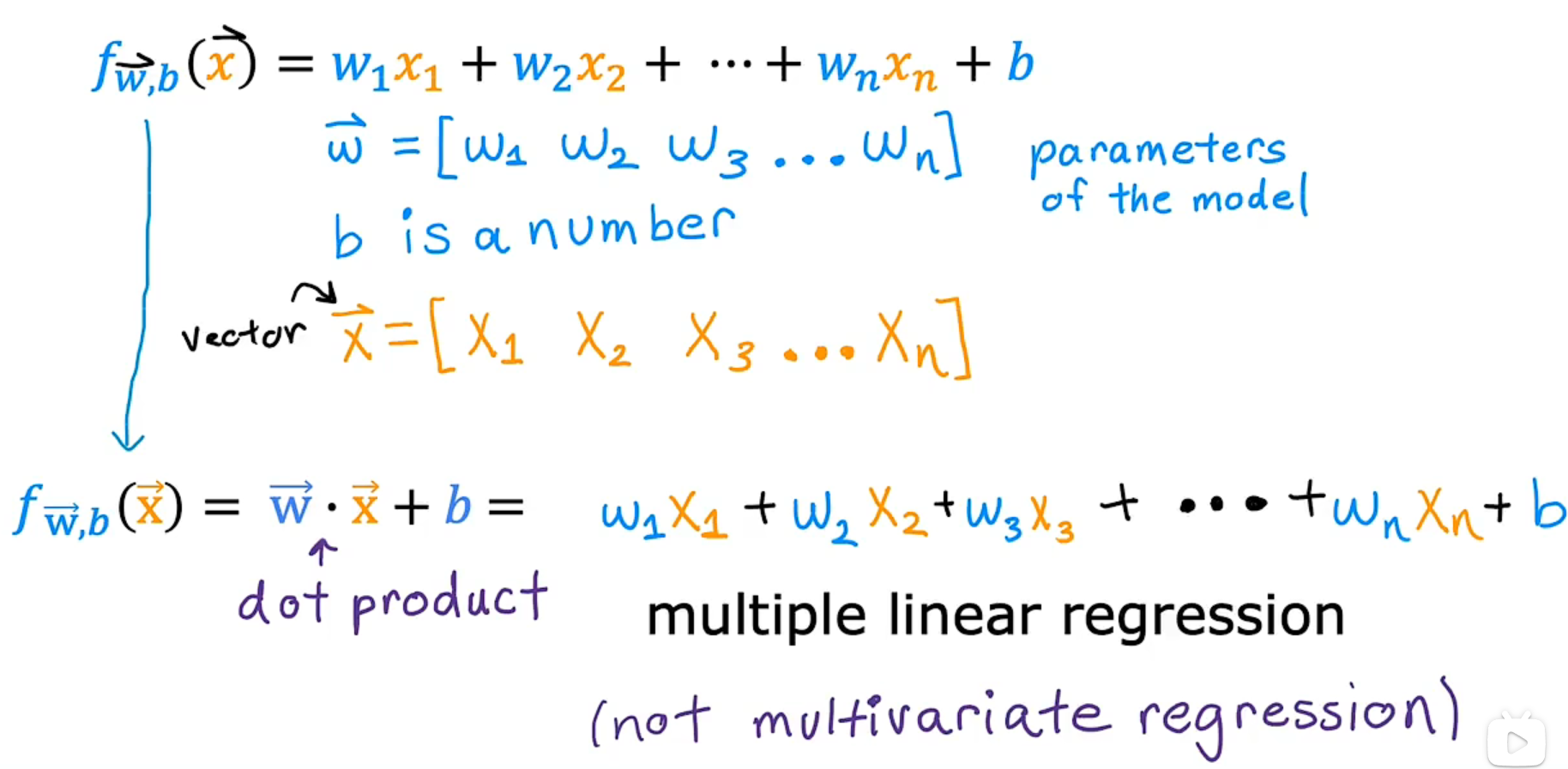
向量化 Vectorization
Numpy:Python中的数值线性代数库
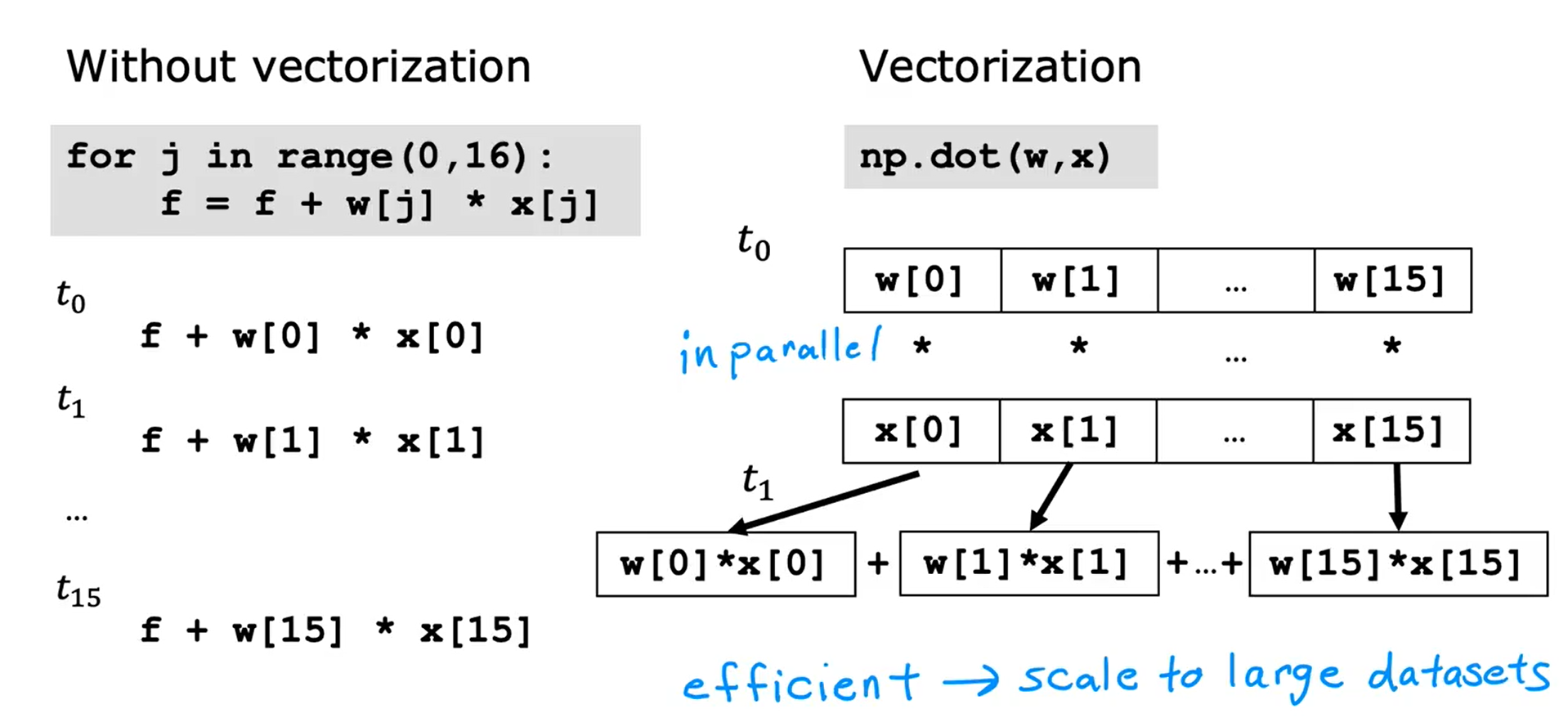
使用向量化计算的优点:
- 代码简洁
- 运行速度较快
np.dot(w, x)
函数是在计算机硬件上通过寻址实现的

★☆

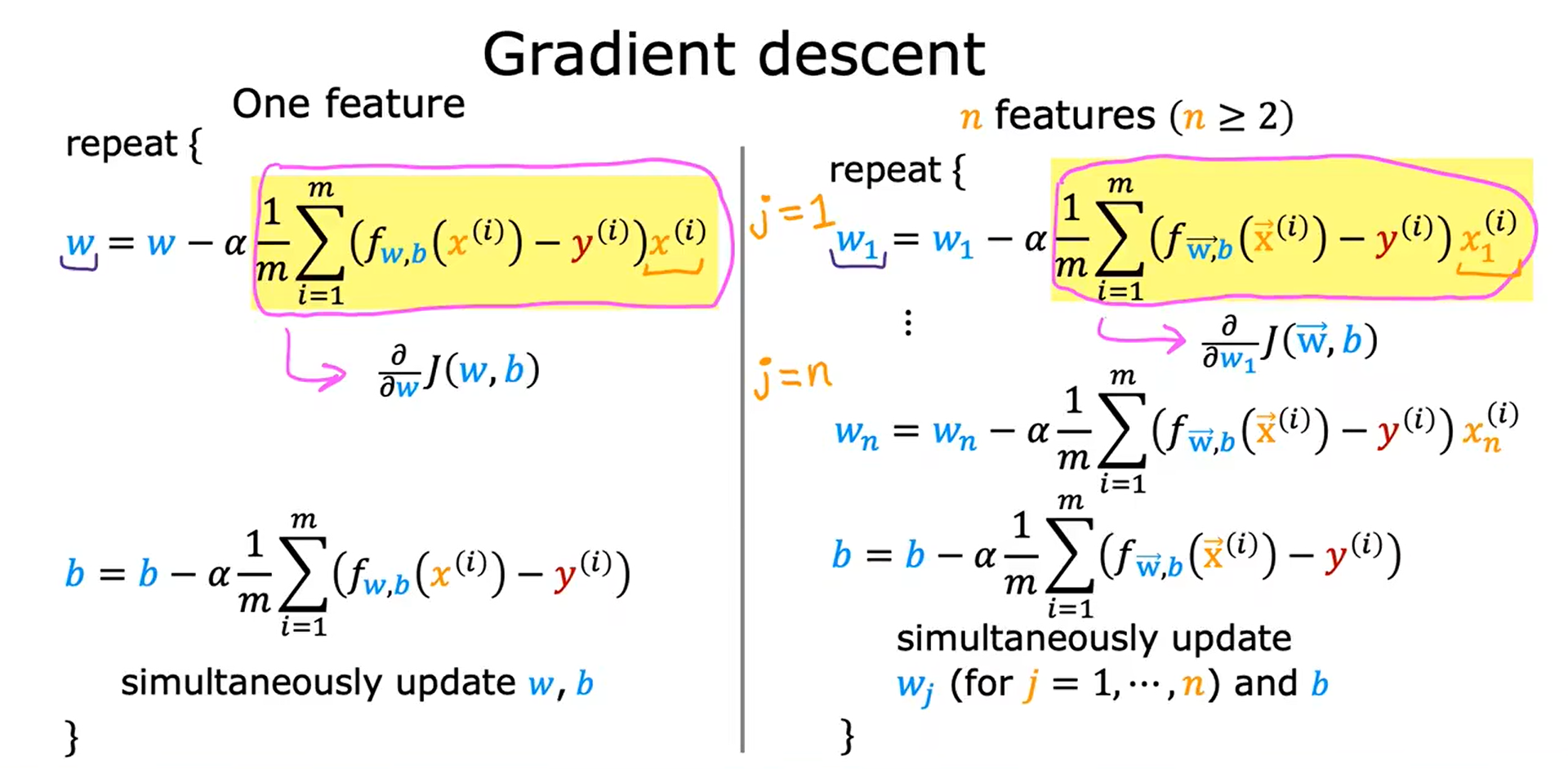
多元线性回归的梯度下降法


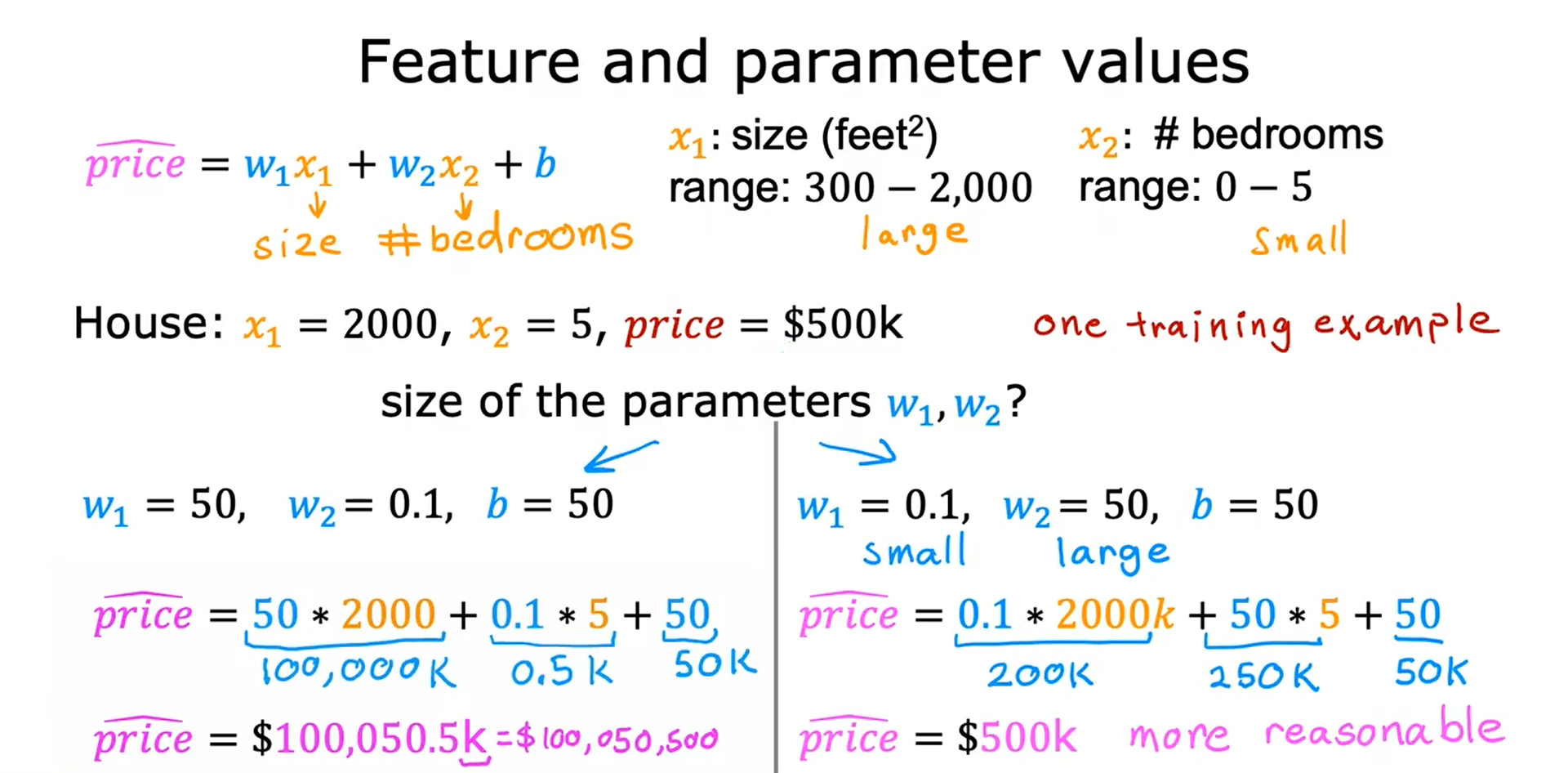
特征放缩 Feature Scaling
当一个特征的可能范围很大时,一个好的模型更有可能学会选择一个相对较小的基准值;同样地,当一个特征的可能值很小时,那么它的参数的合理值就会比较大。
特征放缩的作用:
面对特征数量较多的时候,保证这些特征具有相近的尺度(无量纲化),可以使梯度下降法更快的收敛。
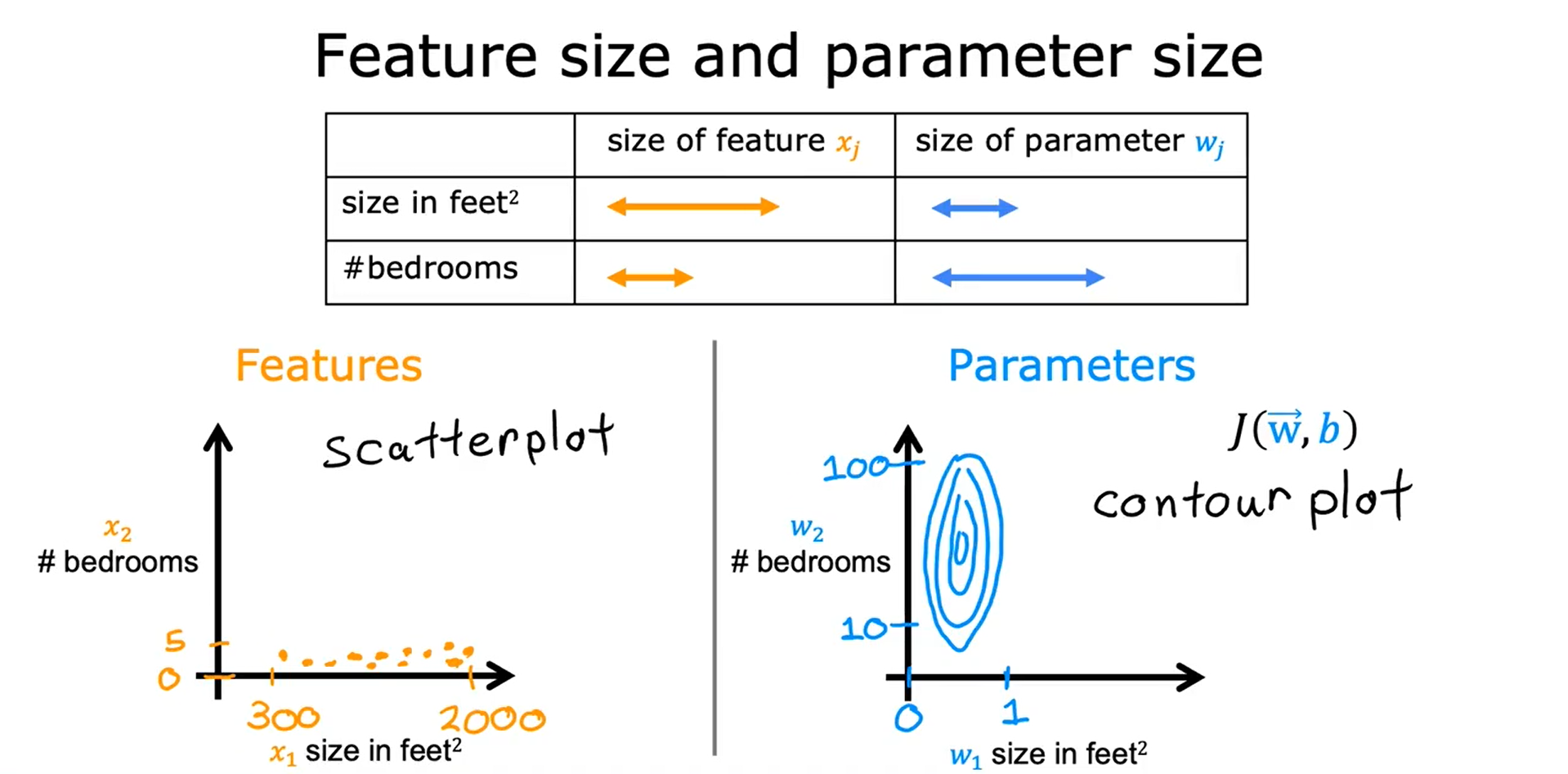
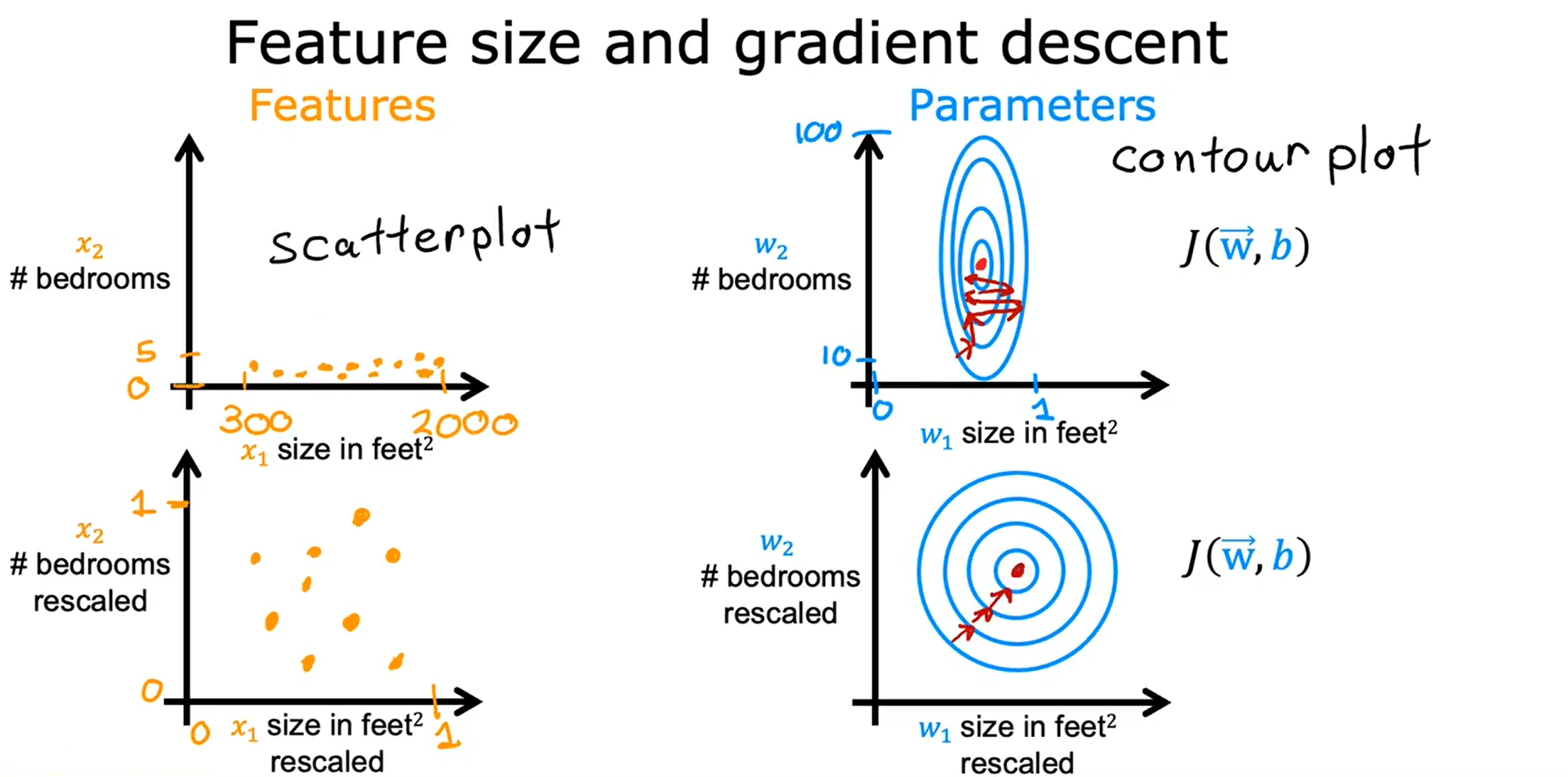
1. 最大值标准化
这个方法是直接除以最大值:
x1的放缩范围:300/2000 ~ 2000/2000,即 0.15 ~ 1
x2的放缩范围:0/5 ~ 5/5,即 0 ~ 1
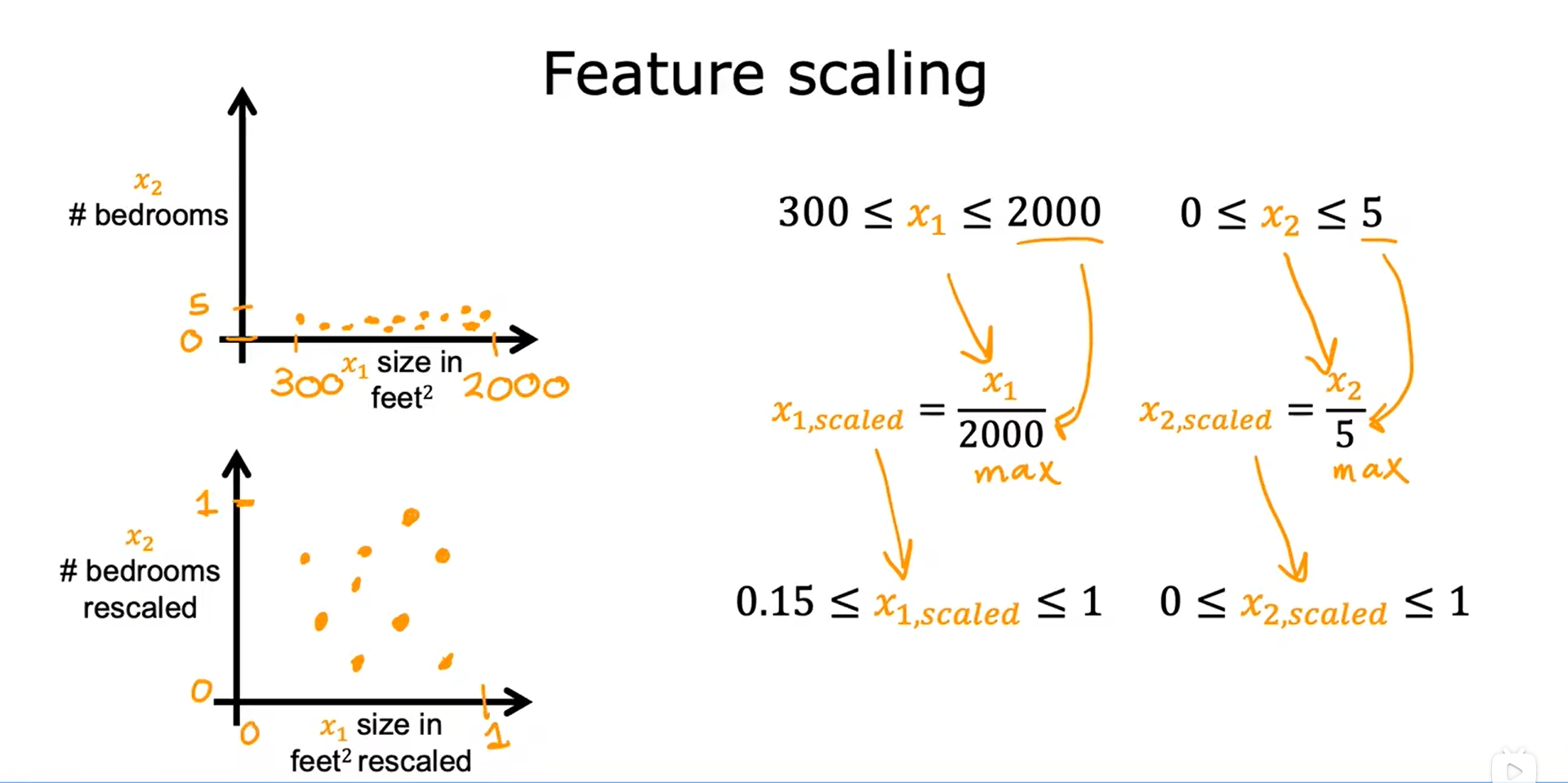
2. 均值归一化 Mean Normalization
这个方法最后的得到的图像是以零为圆心。
步骤:
- 找到训练集上的平均值 μ(此例中,μ1 = 600 作为 x1 的平均值)
x 1 = x 1 − μ 1 m a x − m i n x_1 = \frac{x_1 - \mu_1}{max - min} x1=max−minx1−μ1, 即 x 1 m i n = 300 − 600 2000 − 300 = − 0.18 x_1 min = \frac{300 - 600}{2000 - 300} = -0.18 x1min=2000−300300−600=−0.18, x 1 m a x = 2000 − 600 2000 − 300 = 0.82 x_1 max = \frac{2000 - 600}{2000 - 300} = 0.82 x1max=2000−3002000−600=0.82,得到 − 0.18 ≤ x 1 ≤ 0.82 -0.18 \leq x_1 \leq 0.82 −0.18≤x1≤0.82,此时,x1 已均值归一化。- 找到训练集上的平均值 μ(此例中,μ2 = 2.3 作为 x2 的平均值)
x 2 = x 2 − μ 2 m a x − m i n x_2 = \frac{x_2 - \mu_2}{max - min} x2=max−minx2−μ2,即 x 2 m i n = 0 − 2.3 5 − 0 = − 0.46 x_2min = \frac{0 - 2.3}{5 - 0} = -0.46 x2min=5−00−2.3=−0.46, x 2 m a x = 5 − 2.3 5 − 0 = 0.54 x_2max = \frac{5 - 2.3}{5 - 0} = 0.54 x2max=5−05−2.3=0.54,得到 − 0.46 ≤ x 2 ≤ 0.54 -0.46 \leq x_2 \leq 0.54 −0.46≤x2≤0.54,此时,x2 已均值归一化。

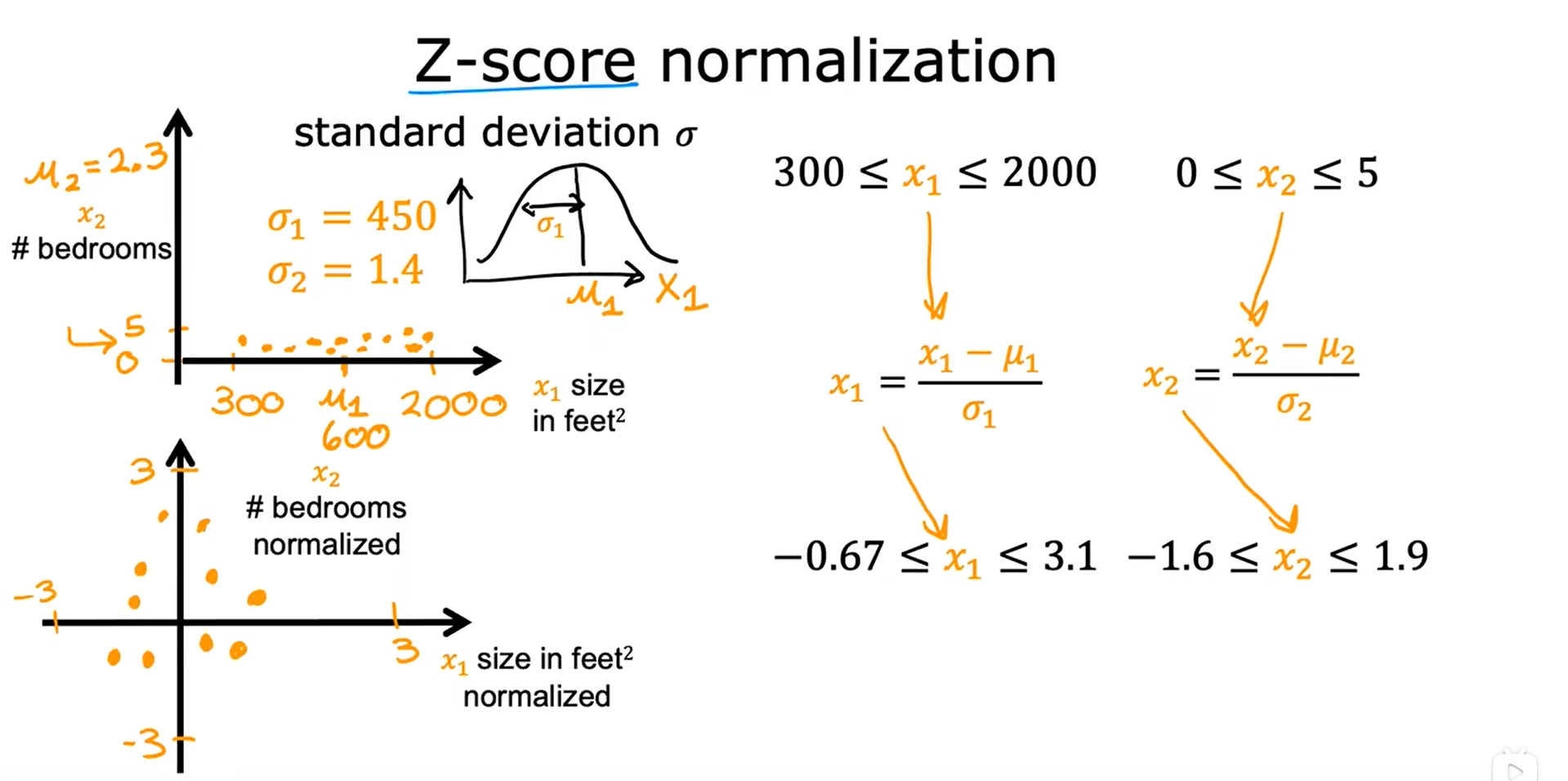
3. Z分数归一化 Z-score normalization
使用这个方法,需要计算每个特征的标准差 σ,首先计算平均值和标准差。
步骤:
- 若 x1 的标准差为 σ1 = 450,平均值 μ1 = 600
x 1 = x 1 − μ 1 σ 1 x_1 = \frac{x_1 - \mu_1}{\sigma_1} x1=σ1x1−μ1, x 1 m i n = 300 − 600 450 = 0.67 , x 2 m a x = 2000 − 600 450 = 3.1 x_1min = \frac{300 - 600}{450} = 0.67, x_2max = \frac{2000 - 600}{450} = 3.1 x1min=450300−600=0.67,x2max=4502000−600=3.1,即 − 0.67 ≤ x 1 ≤ 3.1 -0.67 \leq x_1 \leq 3.1 −0.67≤x1≤3.1- 若 x2 的标准差为 σ2 = 1.4,平均值 μ2 = 2.3
x 2 = x 2 − μ 2 σ 2 x_2 = \frac{x_2 - \mu_2}{\sigma_2} x2=σ2x2−μ2 , x 2 m i n = 0 − 2.3 1.4 = − 1.6 , x 2 m a x = 5 − 2.3 1.4 = 1.9 x_2min = \frac{0 - 2.3}{1.4} = -1.6, x_2max = \frac{5 - 2.3}{1.4} = 1.9 x2min=1.40−2.3=−1.6,x2max=1.45−2.3=1.9,即 − 1.6 ≤ x 2 ≤ 1.9 -1.6 \leq x_2 \leq 1.9 −1.6≤x2≤1.9
下图中的中间上方图像是高斯分布(正态分布) 的标准差。
检查梯度下降是否收敛
确保梯度下降正常工作
1. 创建一个 学习曲线 Learning Curve,试图推测出何时可以停止自己的特定的训练模型
下面这张图可以帮助你看到你的成本函数在每次梯度下降迭代后的变化。
在每次迭代后,成本函数的值应该下降,若在某一次的迭代后成本函数的值增大了,这意味着学习率 α 选择得很差(通常是过大)或 存在漏洞。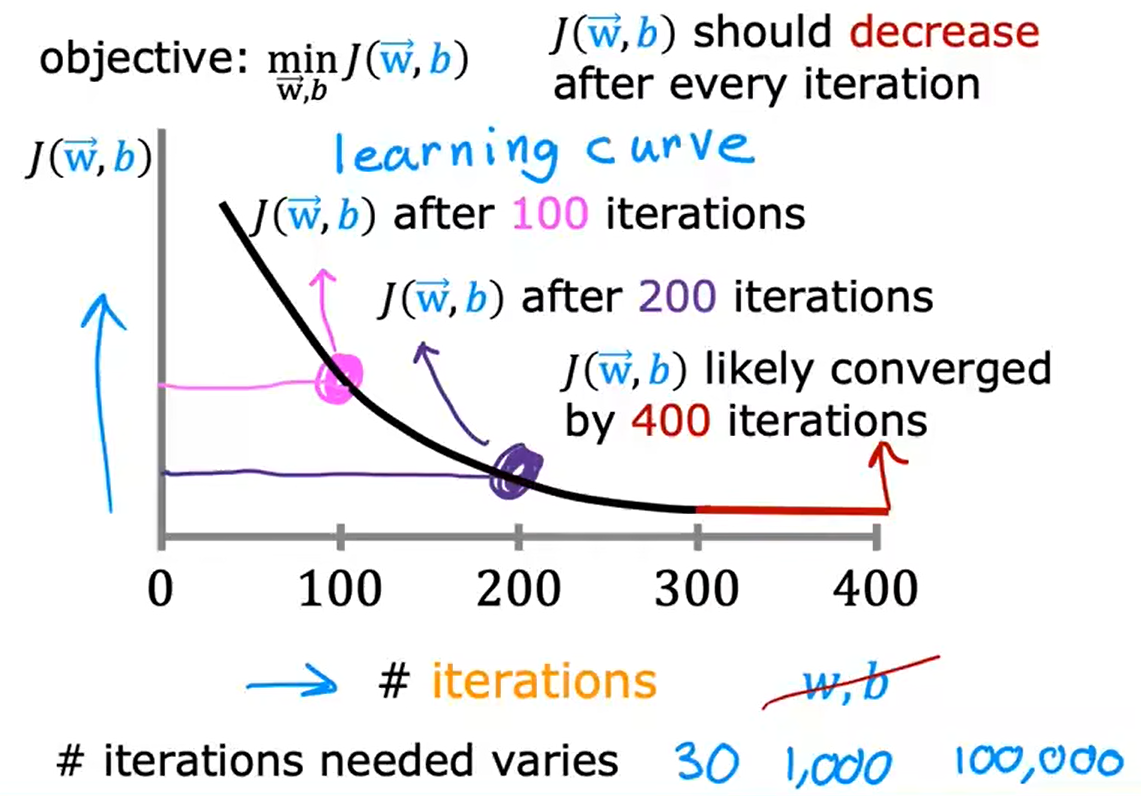
2. 自动收敛测试 Automatic convergence test
- 用 ϵ \epsilon ϵ 来代表一个很小的数字,比如 0.001
- 如果在一次迭代中,成本函数的值下降的幅度小于 ϵ \epsilon ϵ ,那么现在的曲线图像就很可能处于上图中的平坦部分,此时即可宣布收敛,收敛表明此时找到的参数 向量w 和 常数b 很接近成本函数的最小值
- 但通常情况下,选择正确的阈值 ϵ \epsilon ϵ 是相当困难的,所以实际上倾向于使用上面的方法,而不是使用自动收敛检测
学习率的选择
在一个足够小的学习率的情况下,成本函数应该在每次迭代后都减小
- 如果学习率过小,则梯度下降需要花费很多次的迭代才能收敛
- 如果学习率过大,则迭代的时候可能超过最小值,导致成本上升
特征工程 Feature Engineering
通过改造或组合原有特征,利用直觉设计新特征。
Using intuition to design new features, by transforming or combining original features.
取决于对问题有什么见解,而不是仅仅取决于刚开始使用的特征,有时通过定义新特征,可能会得到一个更好的模型。
f
w
⃗
,
b
(
x
⃗
)
=
w
1
∗
x
1
+
w
2
∗
x
2
+
b
i
f
:
a
r
e
a
=
f
r
o
n
t
a
g
e
∗
d
e
p
t
h
s
e
t
:
x
3
=
x
1
∗
x
2
,
(
n
e
w
f
e
a
t
u
r
e
:
x
3
)
f
w
⃗
,
b
(
x
⃗
)
=
w
1
∗
x
1
+
w
2
∗
x
2
+
w
3
∗
x
3
+
b
f_{\vec{w}, b}(\vec{x}) = w_1 * x_1 + w_2 * x_2 + b \\ if: area = frontage * depth \\ set: x_3 = x_1 * x_2, (new feature: x_3)\\ f_{\vec{w},b}(\vec{x}) = w_1 * x_1 + w_2 * x_2 + w_3 * x_3 + b
fw,b(x)=w1∗x1+w2∗x2+bif:area=frontage∗depthset:x3=x1∗x2,(newfeature:x3)fw,b(x)=w1∗x1+w2∗x2+w3∗x3+b

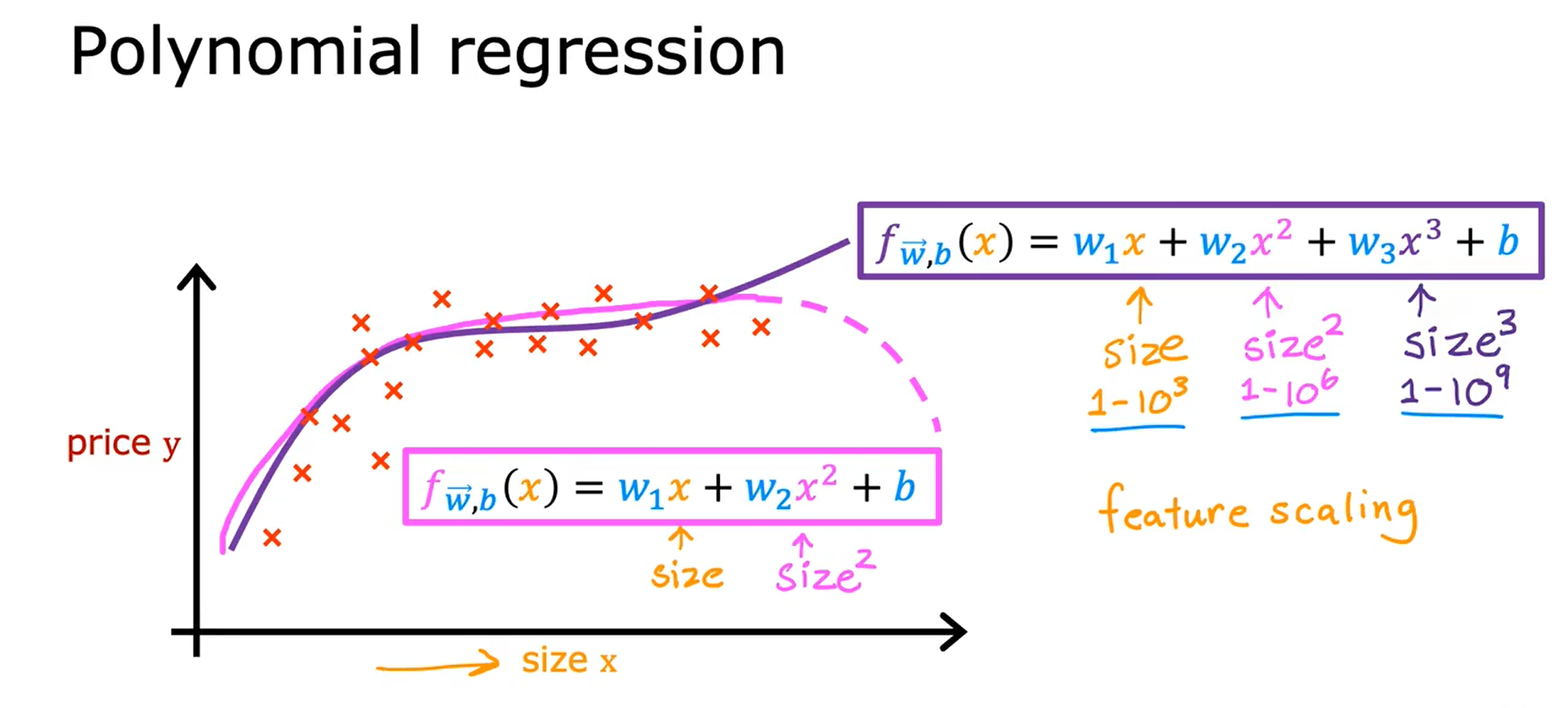
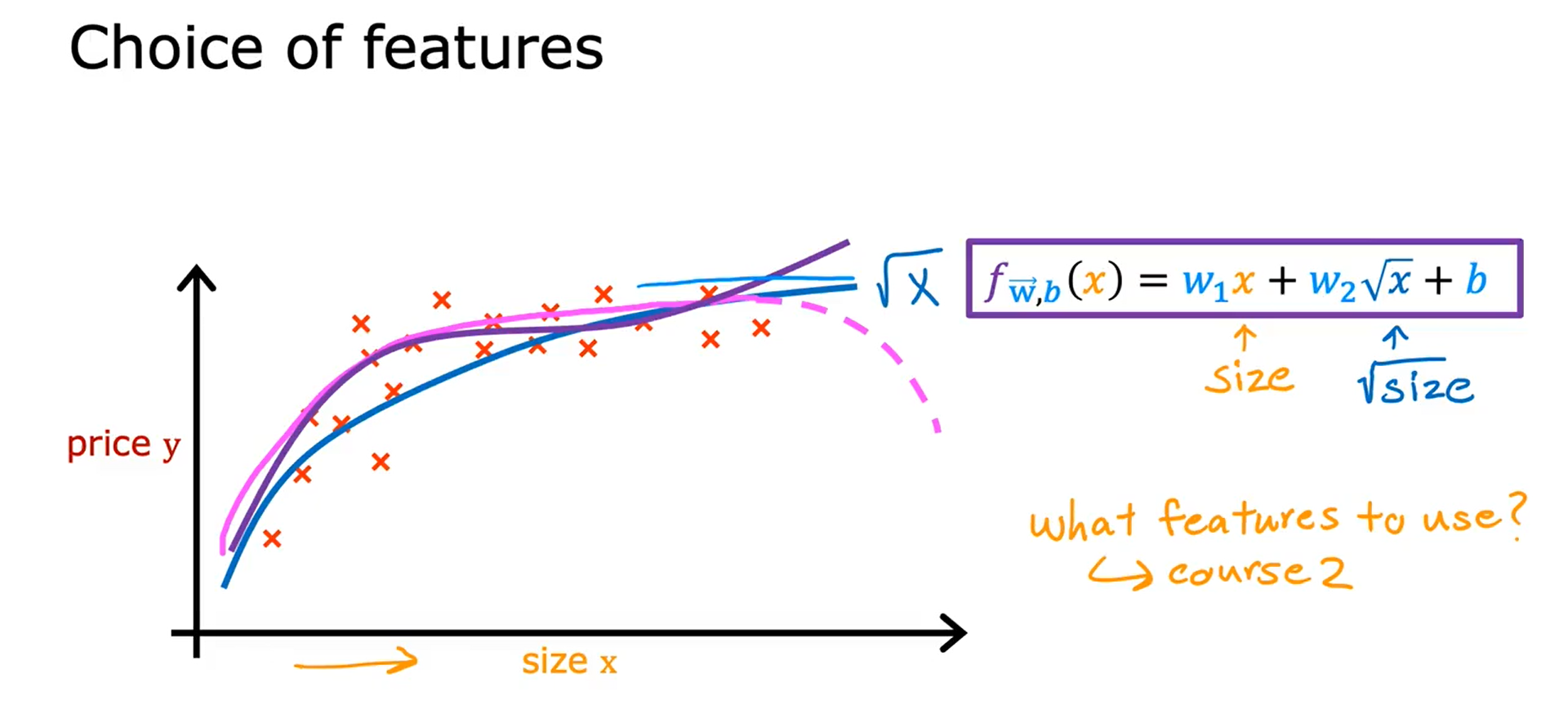
多项式回归 Polynomial Regression
利用多元线性回归和特征工程的思想,提出一种新的多项式回归算法,用来拟合曲线。
链接
- 研究一个因变量与一个或多个自变量间多项式的回归分析方法,称为多项式回归(Polynomial Regression)。
- 如果自变量只有一个时,称为一元多项式回归;如果自变量有多个时,称为多元多项式回归。
- 在一元回归分析中,如果变量y与自变量x的关系为非线性的,但是又找不到适当的函数曲线来拟合,则可以采用一元多项式回归。
分类 Classification
动机 Motivation
使用分类的原因
如果使用线性回归来预测肿瘤是否为恶性这种问题上,则会导致很明显的错误。
线性回归预测了一个数字;分类则只能接受少数几个可能的值中的一个,而不是无限范围内的数字。
这种只有两个可能输出的分类问题,称为二元分类(Binary Classification)。这里的二元指的是在这些问题中只有两个可能的类或两个可能的类别。
QuestionAnswer “y”Is this email spam?no yesIs the transaction fraudulent?no yesIs the tumor malignant?no yes
Answer “y” can only be one of two values, no or yes, false or true, 0 or 1
class = category
决策边界(Decision Boundary)
逻辑回归(Logistic Regression):这个算法可以避免产生下图的效果,逻辑回归虽然是带有回归二字,但却是用来 分类 的。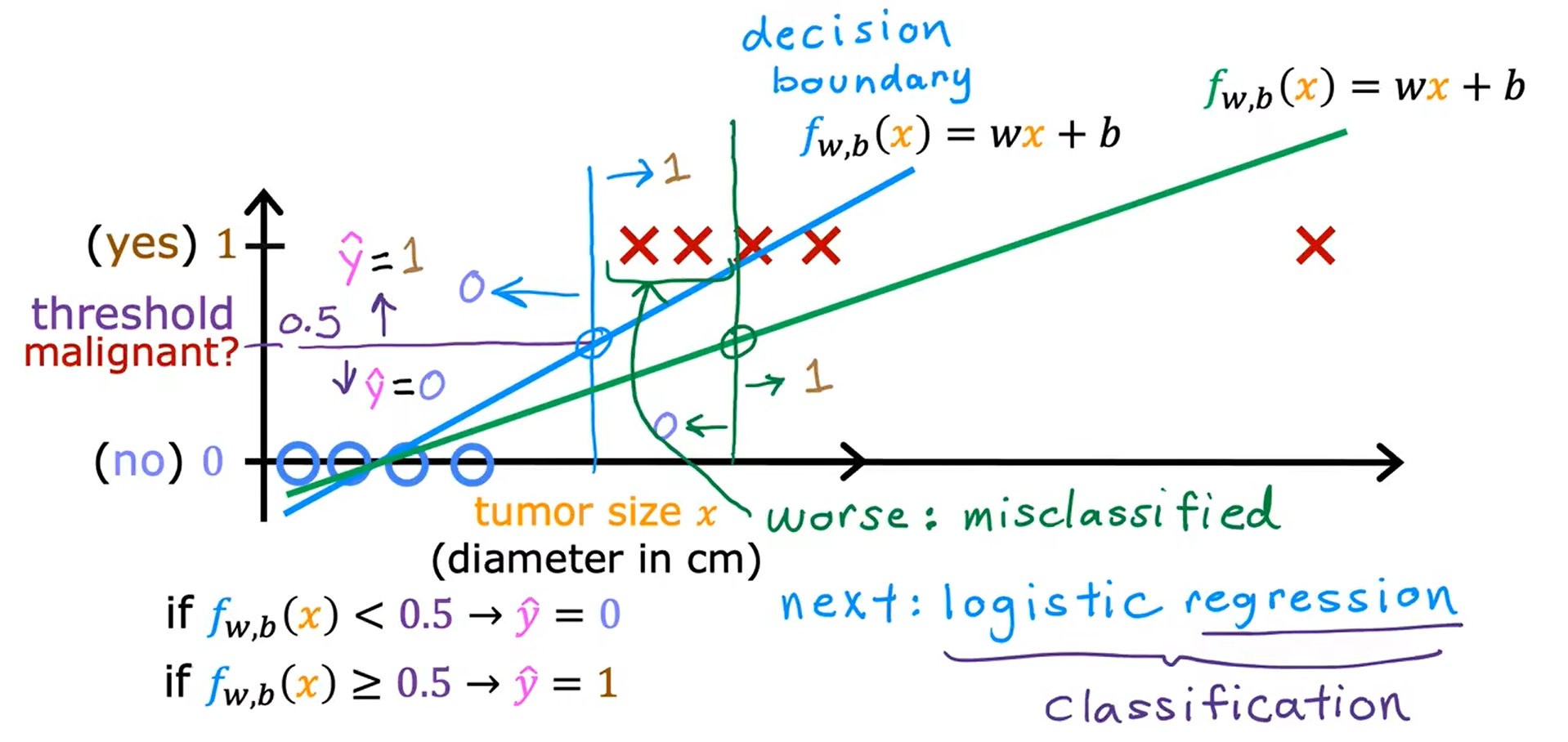
逻辑回归 Logistic Regression
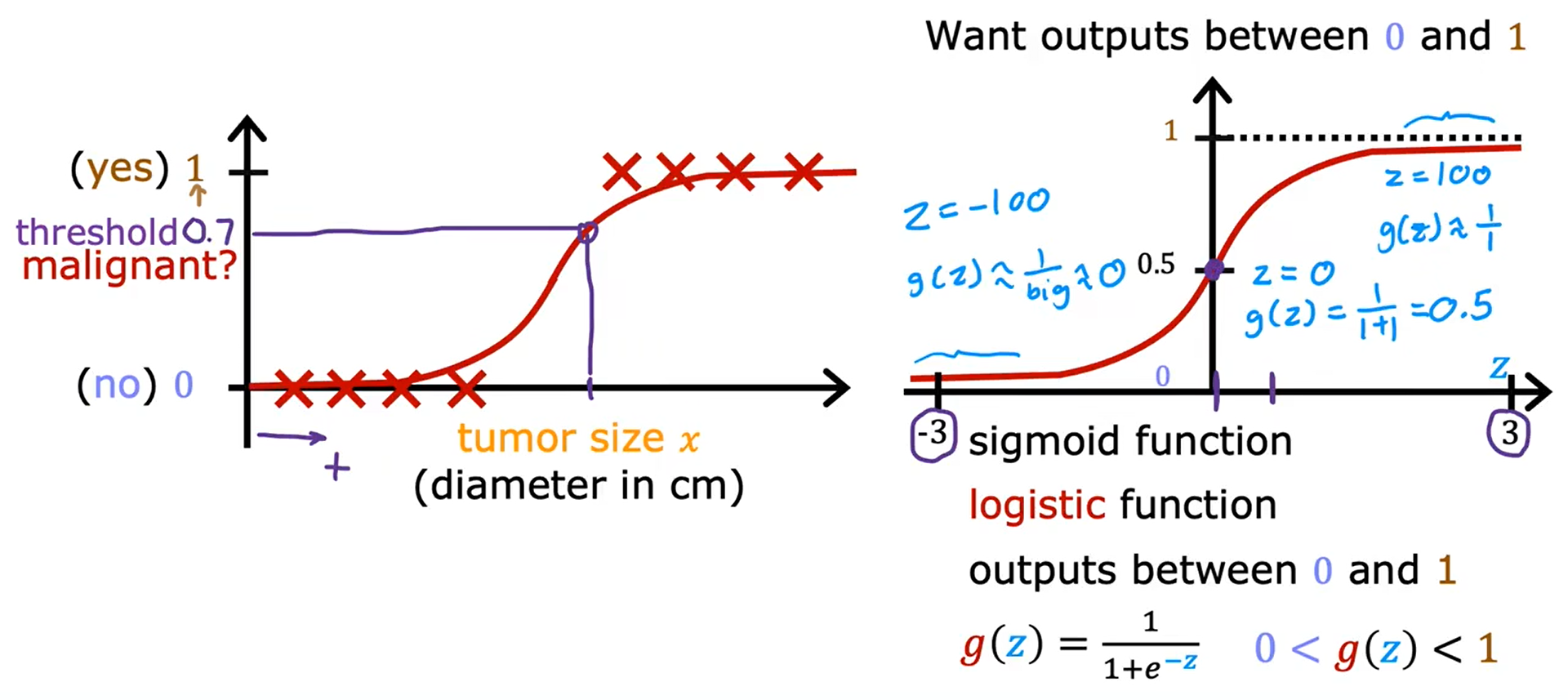
Sigmoid Function(Logistic Function)(乙状结肠函数,后勤函数,S型函数)
逻辑回归可以用来拟合相当复杂的数据。
输出的范围是:0 ~ 1
g
(
z
)
=
1
1
+
e
−
z
,
0
<
g
(
z
)
<
1
g(z) = \frac{1}{1 + e^{-z}}, 0 < g(z) < 1
g(z)=1+e−z1,0<g(z)<1
逻辑回归:
f
w
⃗
,
b
(
x
⃗
)
=
g
(
w
⃗
⋅
x
⃗
+
b
)
=
1
1
+
e
−
(
w
⃗
⋅
x
⃗
+
b
)
f_{\vec{w},b}(\vec{x}) = g(\vec{w} · \vec{x} + b) = \frac{1}{1 + e^{-(\vec{w} · \vec{x} + b)}}
fw,b(x)=g(w⋅x+b)=1+e−(w⋅x+b)1
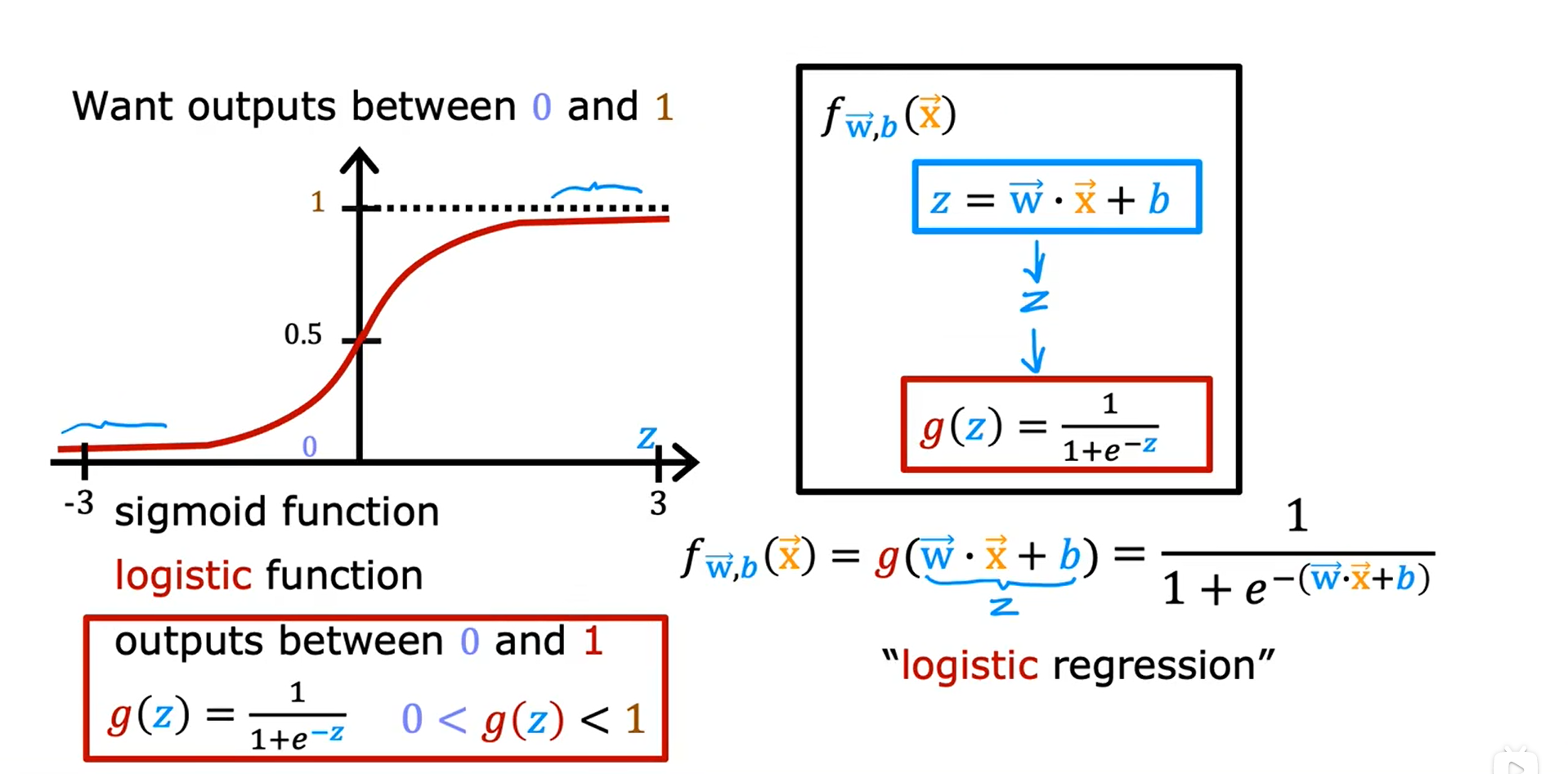

决策边界 Decision Boundary
可以设置一个阈值,当预测的数值高于这个阈值时,可以判定为1,低于这个阈值时,可以判定为0。
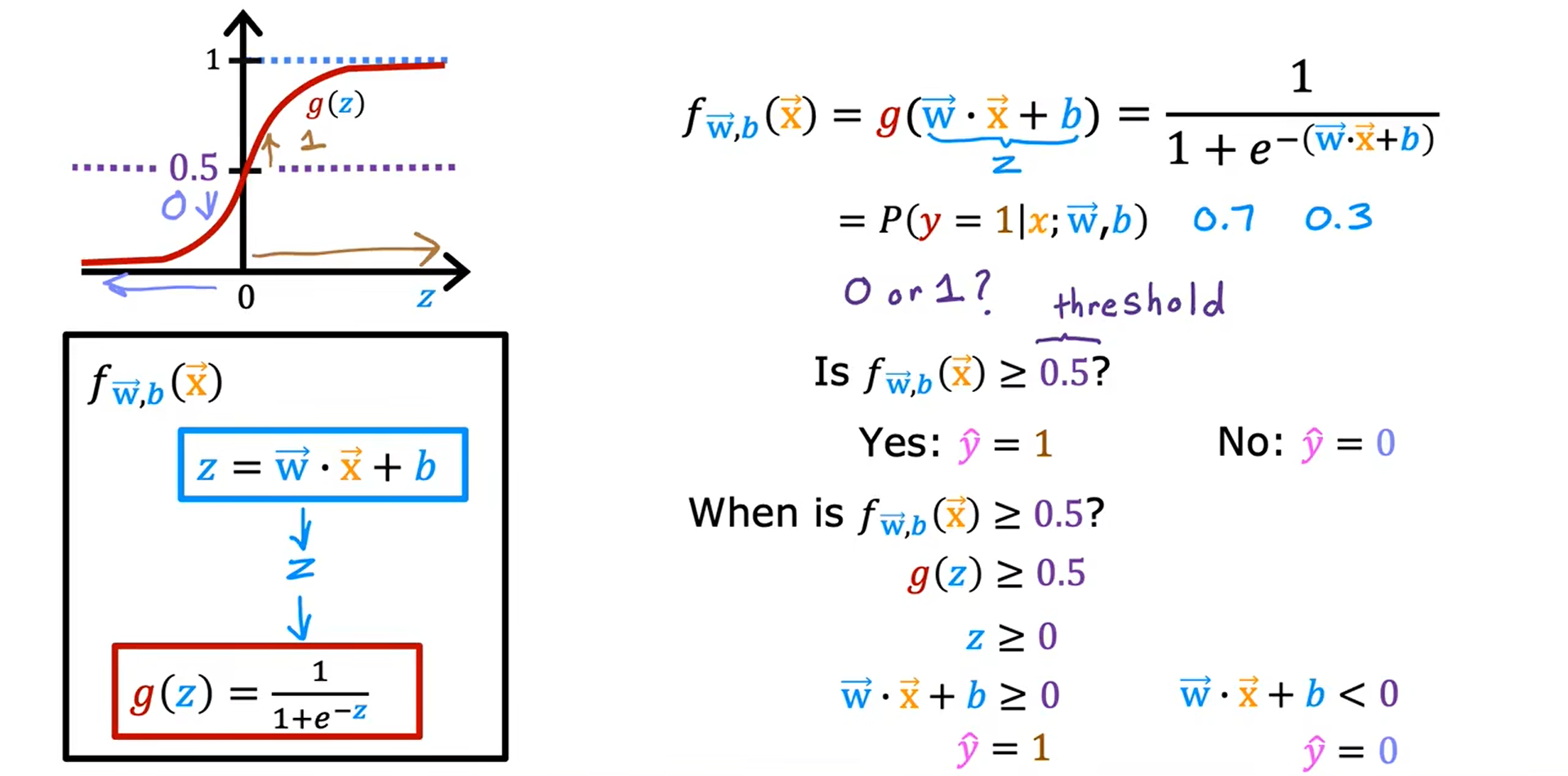
例一:
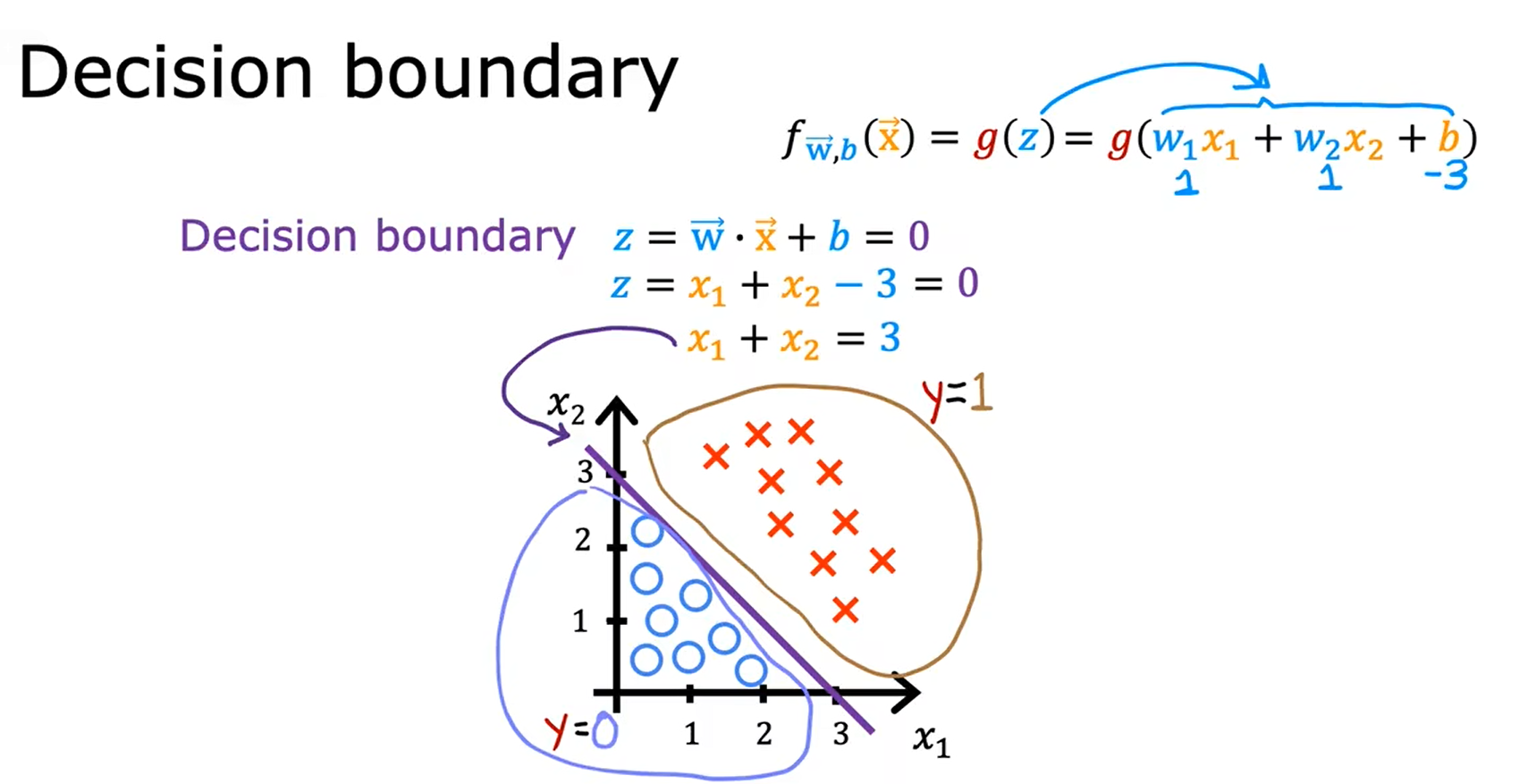
例二:

例三:

逻辑回归的成本函数函数 Cost Function For Logistic Regression
成本函数用来衡量一组特定的参数与训练数据的匹配程度,从而提供了一种更好的方法来尝试选择更好的参数。
误差平方的成本函数不是逻辑回归的理想成本函数,平方误差成本函数是线性回归中最常用的函数。
单一训练子集的损失(L),并作为学习算法预测的函数:
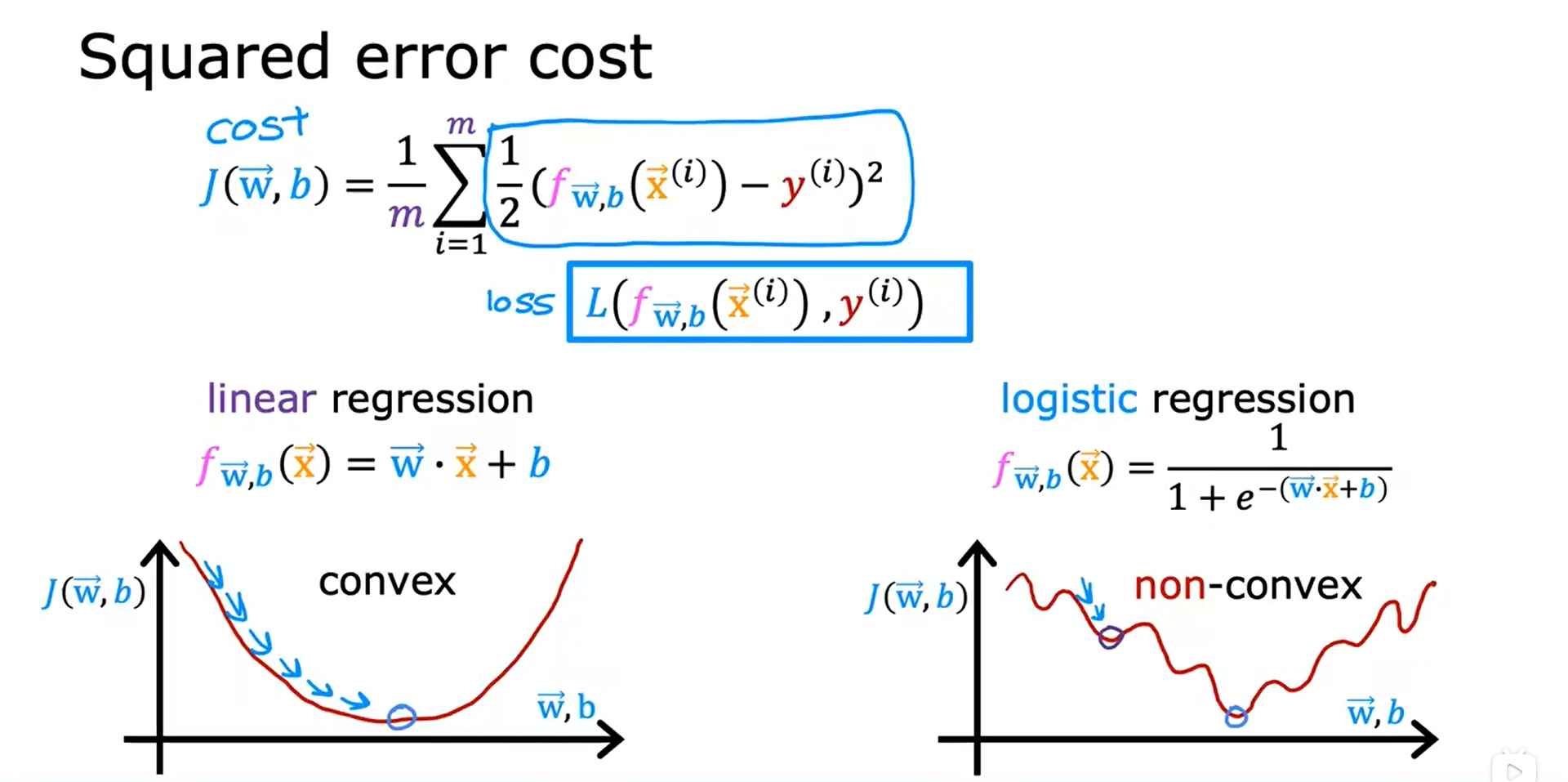
逻辑回归的损失函数
当
y
(
i
)
y^{(i)}
y(i) 等于1时,损失函数会帮助算法做出更准确的预测,因为当它预测的值接近1时,损失是最低的。

当
y
(
i
)
y^{(i)}
y(i) 等于0时,
f
w
⃗
,
b
(
x
(
i
)
⃗
)
f_{\vec{w},b}(\vec{x^{(i)}})
fw,b(x(i)) 越远离
y
(
i
)
y^{(i)}
y(i) ,损失越大。
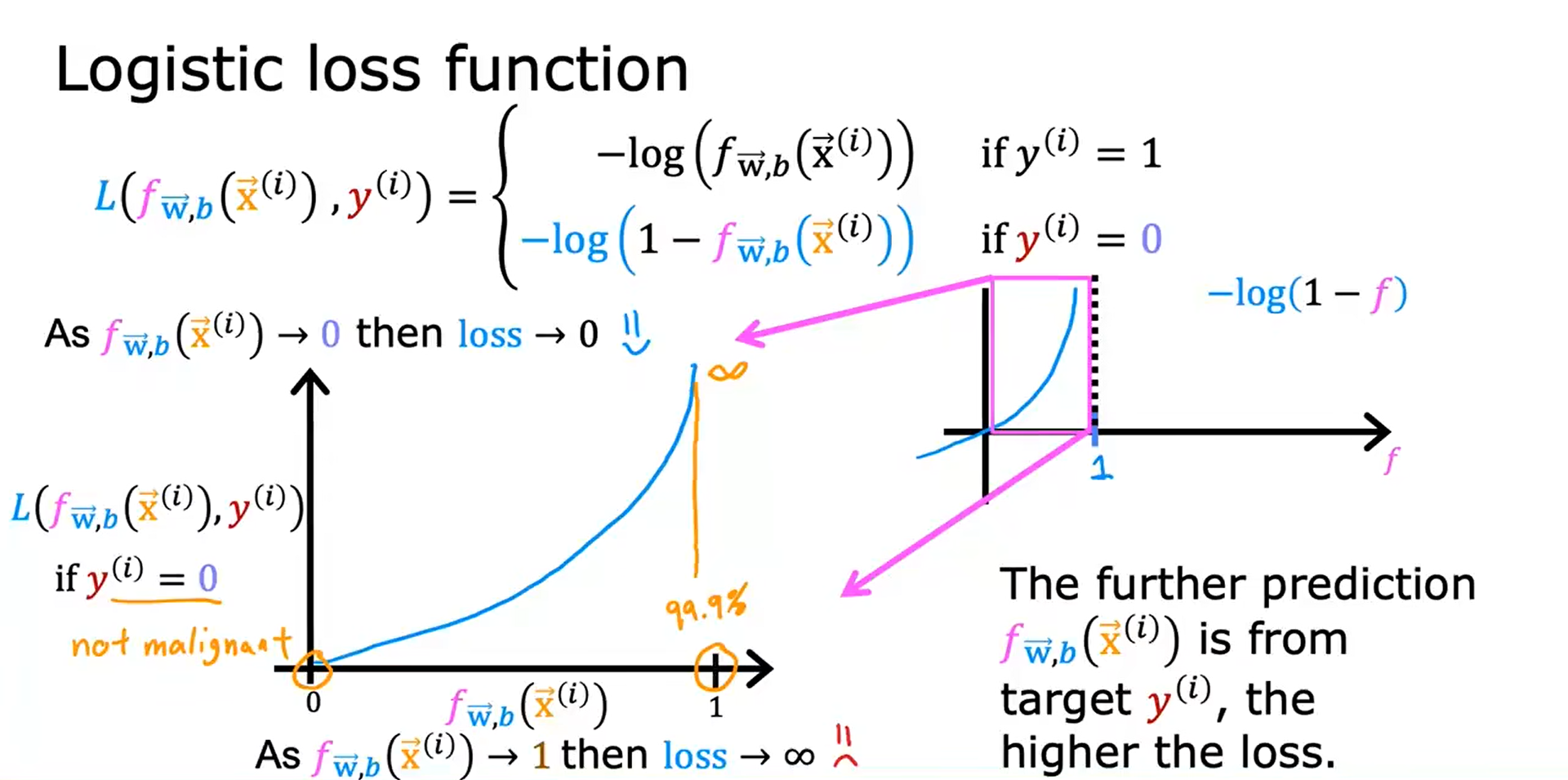
总结,逻辑回归的损失函数的定义如下图所示,并且通过选择损失函数,总代价函数是凸的,因此可以可靠地使用极大的下降来获得全局最小值。

逻辑回归的简化版成本函数
就是将两个表达式合成一个,不管
y
(
i
)
y^{(i)}
y(i) 为1还是0,都会得到原来的表达式:

成本函数J 是整个训练集m个例子中的平均损失值。
这个特殊的成本函数是从统计学中推导出来的,它使用了最大似然估计的统计原理。

梯度下降实现 Gradient Descent Implementation
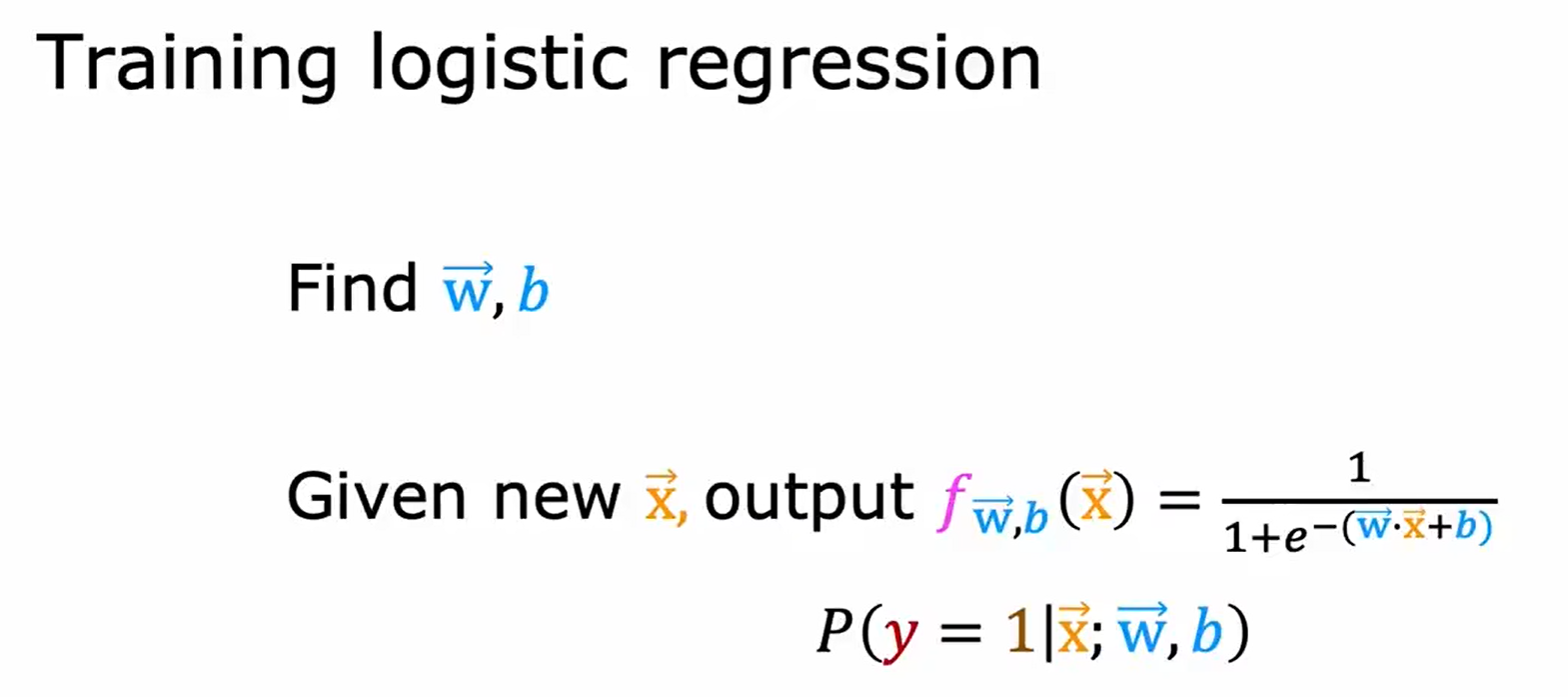

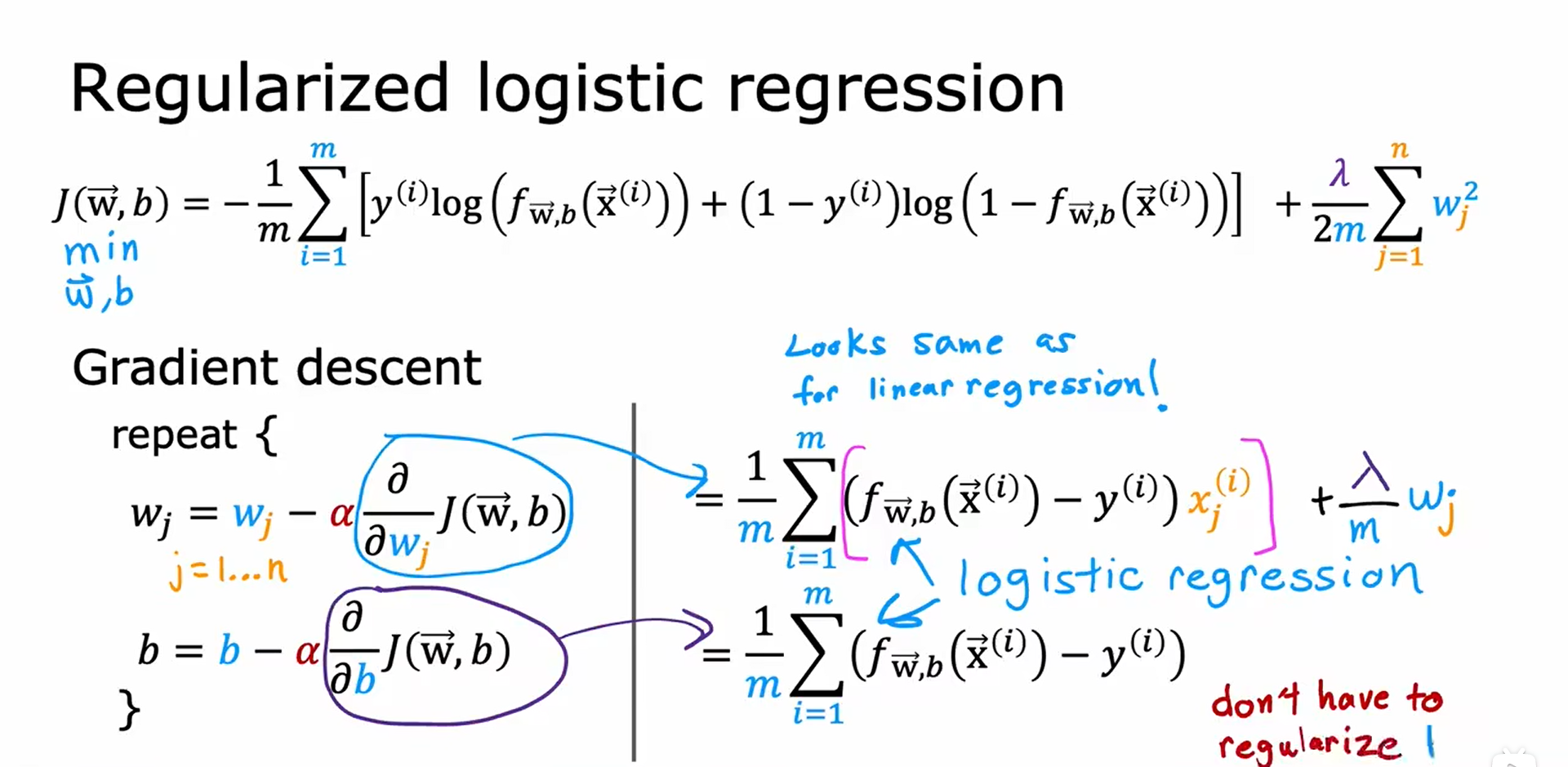
因为线性回归模型和逻辑回归模型的具体模型算法不一样,所以尽管在下图中写的代码看起来是一样的,但实际上是两种截然不同的算法。

过拟合的问题 The Proble Of Overfitting
过拟合时,尽管在训练中做得很好,但却不能很好的概括新的例子。
Regression example:
右侧的过拟合(高方差),左侧的欠拟合(高偏差),中间的刚刚好(泛化)。
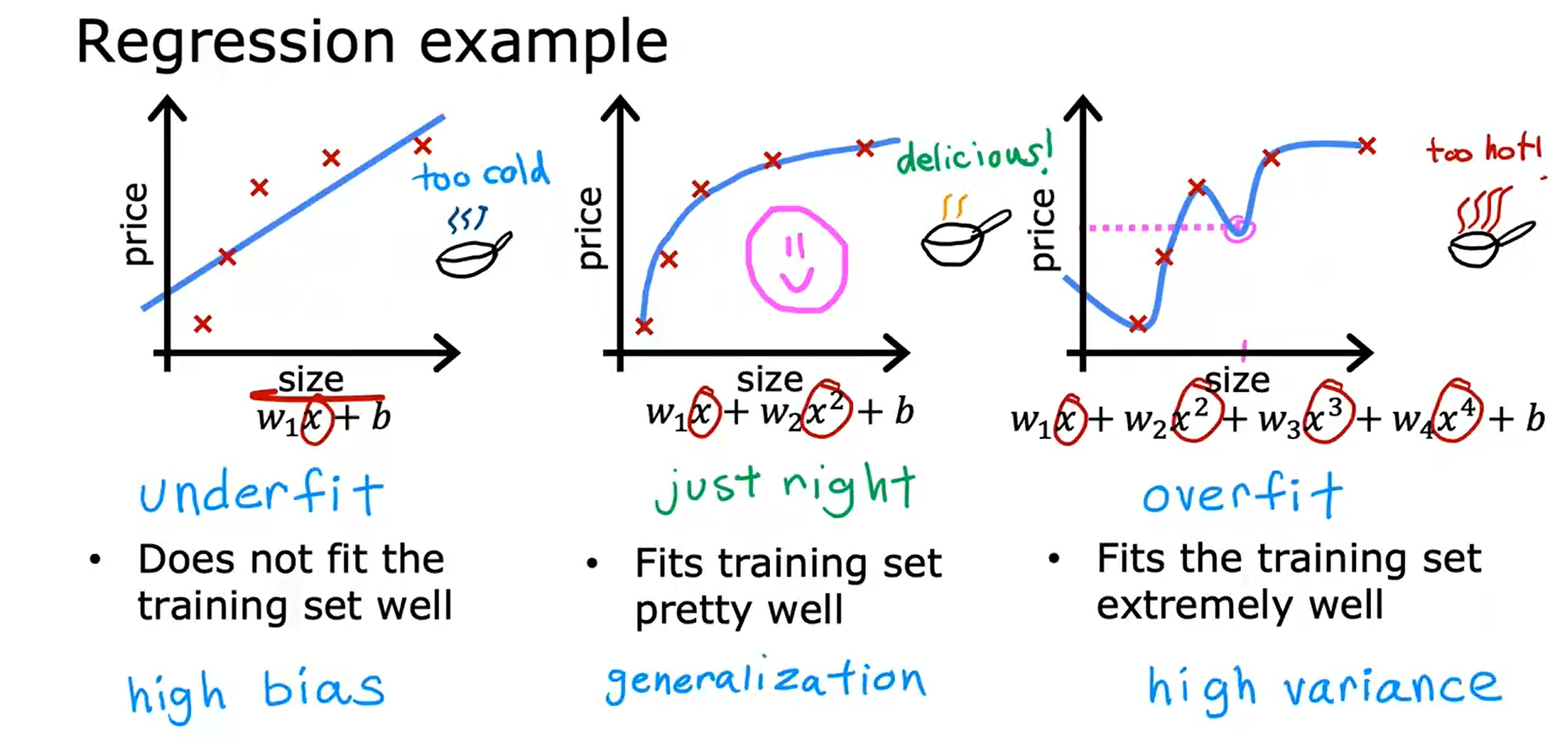
Classification example:
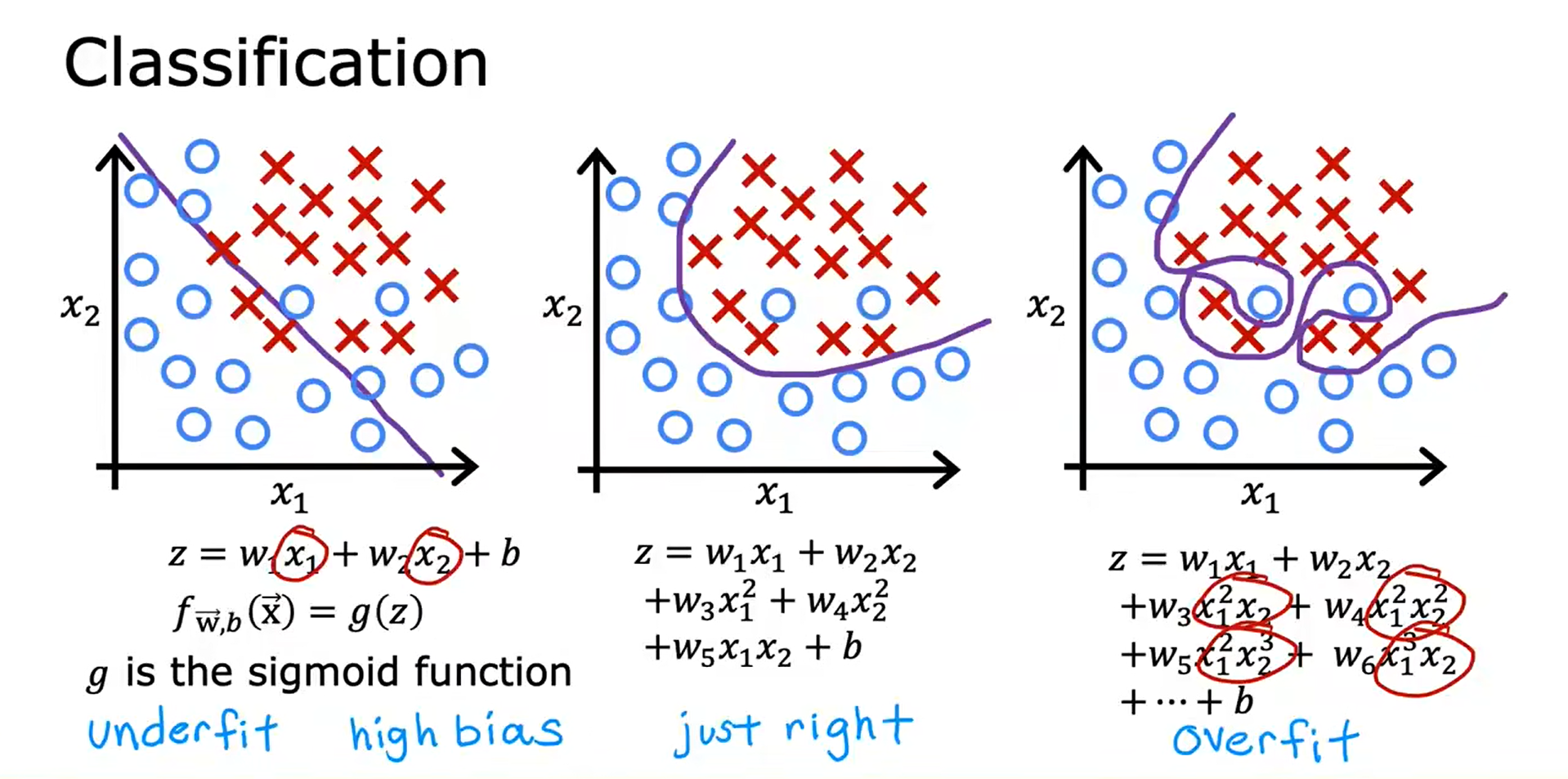
解决过拟合 Addressing Overfitting
方案:
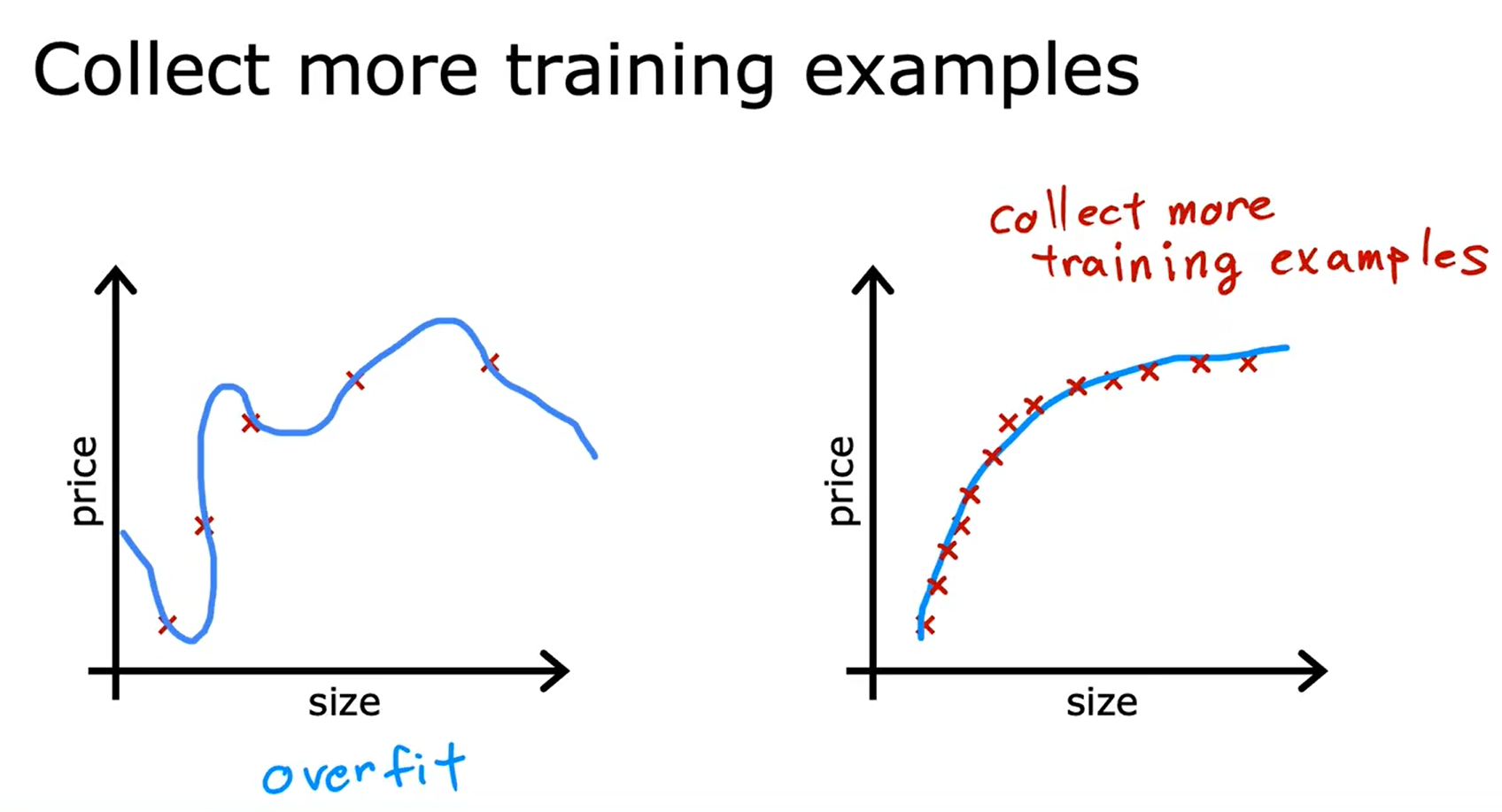
- 收集更多的训练数据(Collect more training examples, Collect more data)
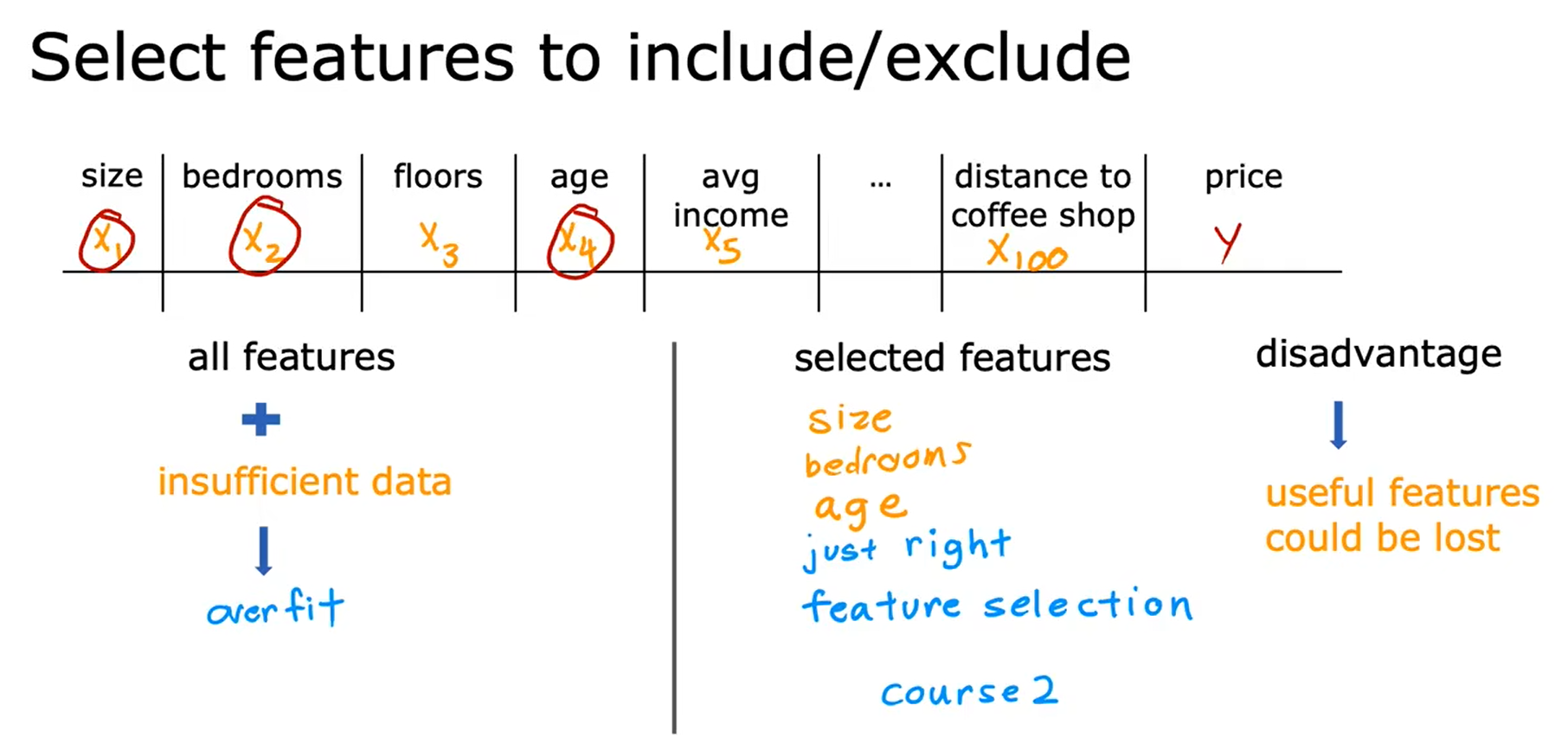
- 选择要包含/排除的特性(Select features to include/exclude, Select features)
- 正规化(Regularization, Reduce size of parameters) - 减少参数的大小,正规化是一种更温和地减少一些特征影响的方法。- 正规化鼓励学习算法缩小参数的值,而不一定要求参数被设置为零。- 正规化所做的是保持所有的特征,但只是防止某个特征产生过大的影响。
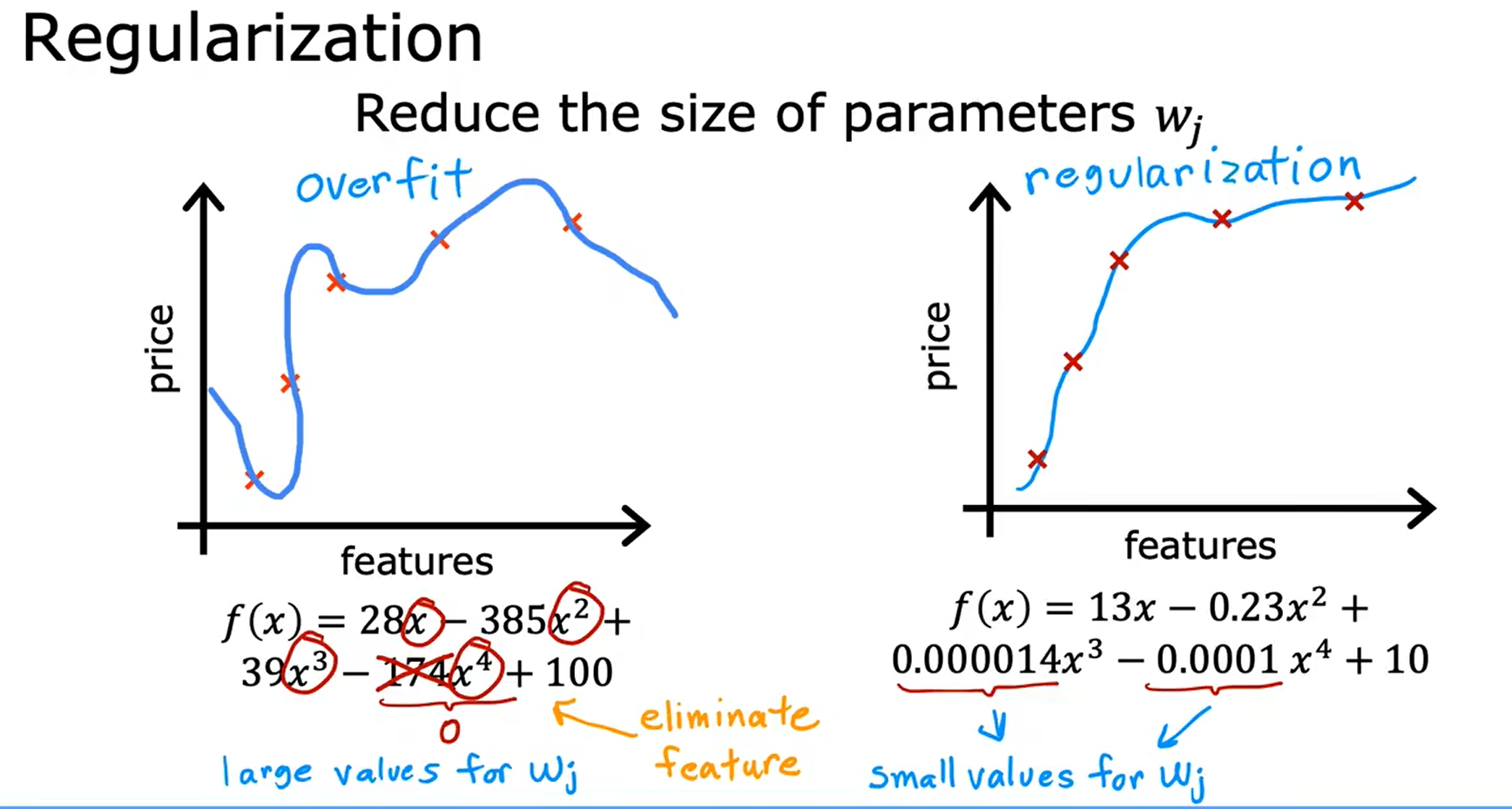
正则化代价函数 Cost Function With Regularization
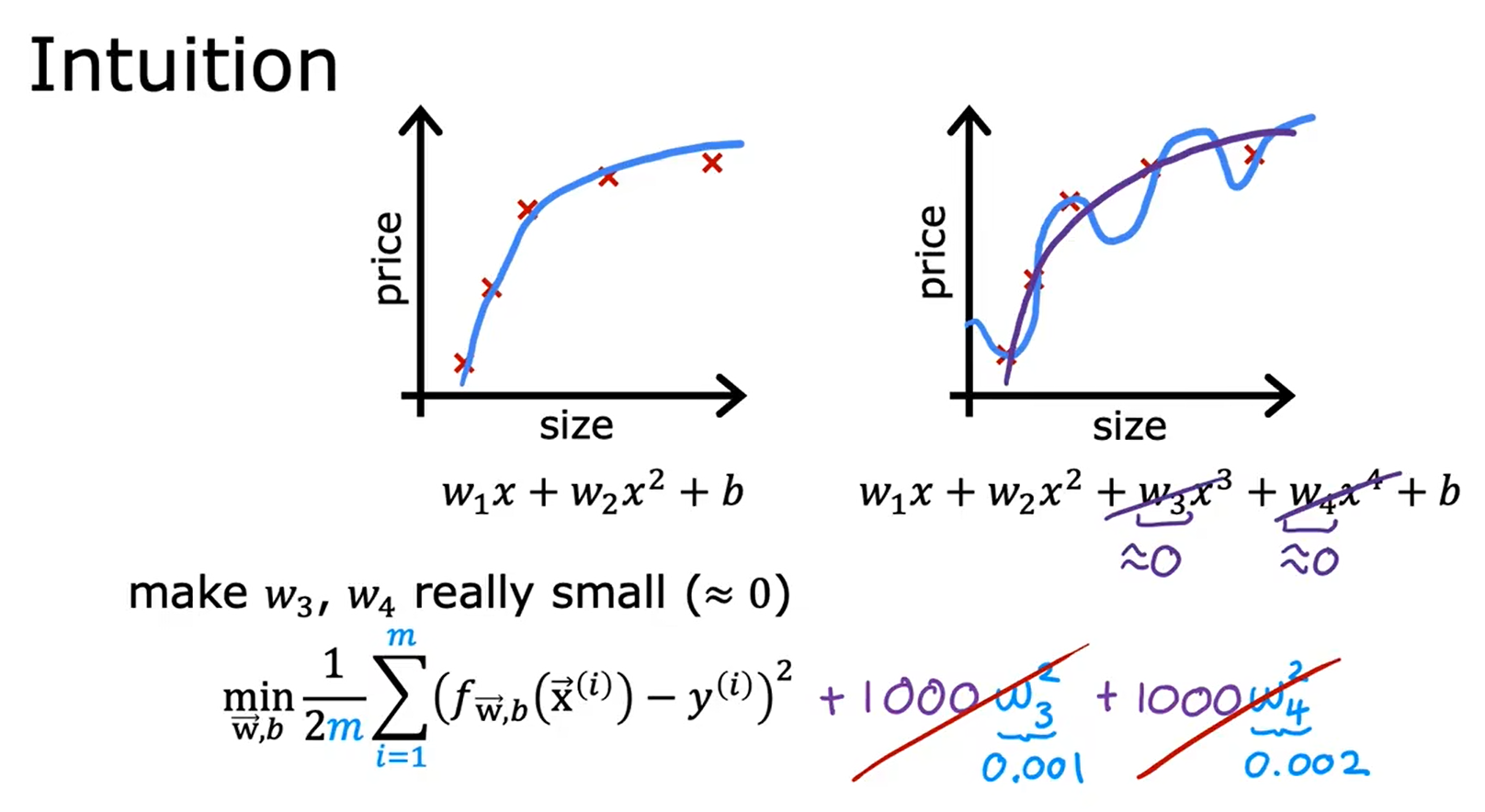
正则化参数:λ(Regularization Parameter),λ > 0
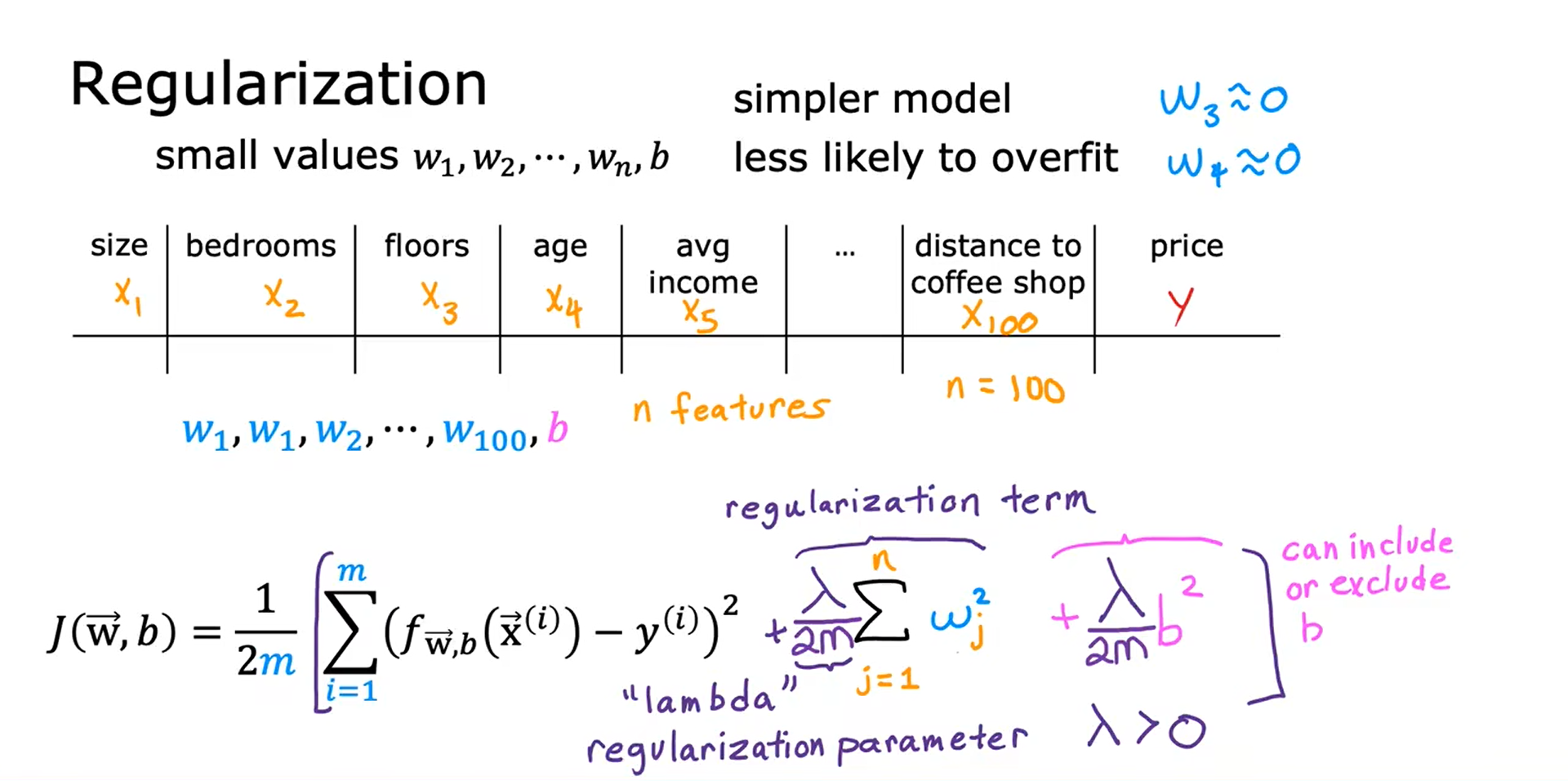
正则化线性回归的成本函数:
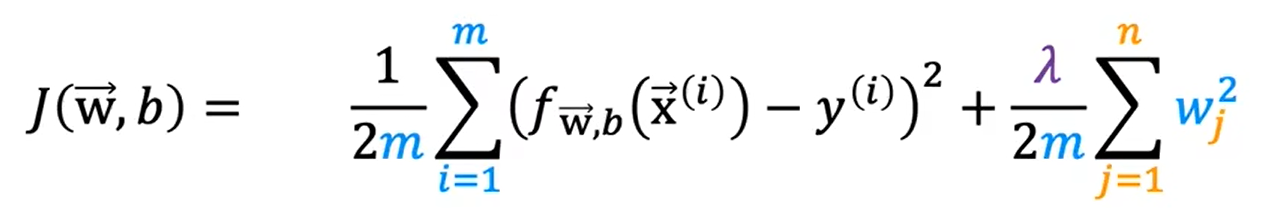
两个极端情况下的正则化参数 λ:
- 若 λ = 0,即没有使用正则化项,则最终会过拟合。
- 若 λ = 1 0 10 10^{10} 1010,则使其最小化的唯一方法是让w的值非常接近于0,则 f(x) = b 会成立,会导致欠拟合。

正则化线性回归 Regularized Linear Regression
实现正则化线性回归的梯度下降



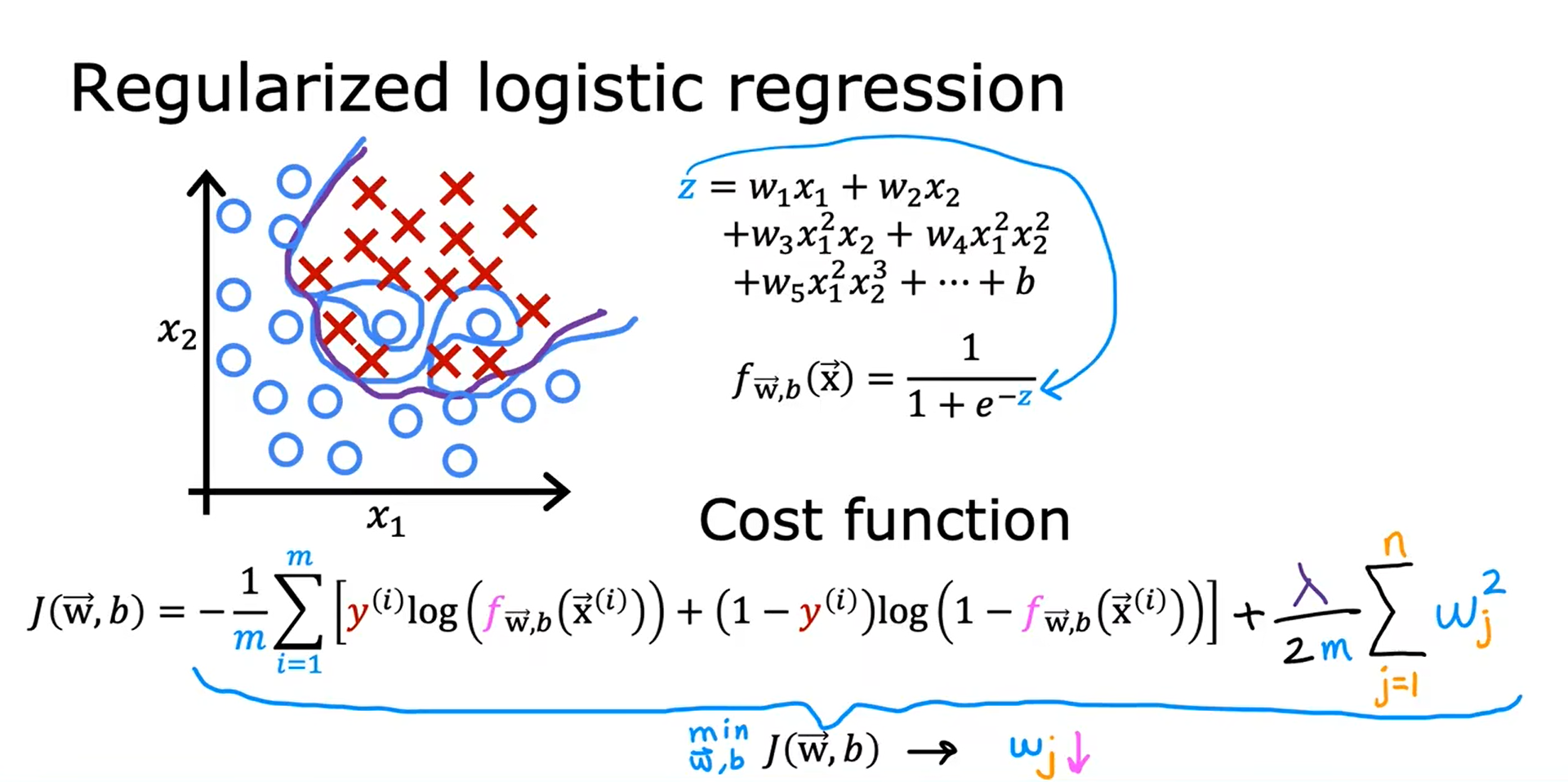
正则化逻辑回归 Regularized Logistic Regression
版权归原作者 YYYMarshal 所有, 如有侵权,请联系我们删除。