目录
一、硬间隔SVM
sklearn中没有实现硬间隔SVM的类,因为它并不实用,但我们可以通过将正则化项
C
C
C 设置的足够大(例如
C
=
1
0
6
C=10^6
C=106)来模拟硬间隔SVM。
考虑如下的二分类问题:
在平面直角坐标系中,设正样例为
x 1 = ( 1 , 2 ) , x 2 = ( 2 , 3 ) , x 3 = ( 3 , 3 ) \boldsymbol{x}_1=(1,2), \boldsymbol{x}_2=(2, 3), \boldsymbol{x}_3=(3, 3) x1=(1,2),x2=(2,3),x3=(3,3),负样例为 x 4 = ( 2 , 1 ) , x 5 = ( 3 , 2 ) \boldsymbol{x}_4=(2, 1), \boldsymbol{x}_5=(3,2) x4=(2,1),x5=(3,2),试求最大间隔超平面。
不难看出,我们的SVM应使用线性核。
在进行下一步之前,我们先来介绍一下sklearn中有关SVM的类
sklearn.svm.SVC()
。
1.1 sklearn.svm.SVC()
本文并不会讲解所有的参数,需要进一步了解的读者可自行参阅官方文档。
1.1.1 数据集
机器学习中,数据集通常以如下的形式表示:
D
=
{
(
x
1
,
y
1
)
,
(
x
2
,
y
2
)
,
⋯
,
(
x
n
,
y
n
)
}
D=\{(\boldsymbol{x}_1,y_1),(\boldsymbol{x}_2,y_2),\cdots,(\boldsymbol{x}_n,y_n)\}
D={(x1,y1),(x2,y2),⋯,(xn,yn)}
其中每个
x
i
\boldsymbol{x}_i
xi 是示例,
y
i
y_i
yi 是示例对应的标签,
(
x
i
,
y
i
)
(\boldsymbol{x}_i,y_i)
(xi,yi) 合起来称为样例。为接下来叙述方便起见,这里假设
x
i
\boldsymbol{x}_i
xi 是行向量。
令
X
=
[
x
1
x
2
⋮
x
n
]
,
y
=
[
y
1
y
2
⋮
y
n
]
X= \begin{bmatrix} \boldsymbol{x}_1 \\ \boldsymbol{x}_2 \\ \vdots \\\boldsymbol{x}_n \end{bmatrix},\quad y= \begin{bmatrix} y_1 \\ y_2 \\ \vdots \\y_n \end{bmatrix}
X=⎣⎢⎢⎢⎡x1x2⋮xn⎦⎥⎥⎥⎤,y=⎣⎢⎢⎢⎡y1y2⋮yn⎦⎥⎥⎥⎤
则称
X
X
X 为示例矩阵,
y
y
y 为标签向量。例如,对于上述的二分类问题,我们的
X
,
y
X,y
X,y 分别为:
X =[[1,2],[2,3],[3,3],[2,1],[3,2]]
y =[1,1,1,-1,-1]
设样例数为
samples
,特征数为
features
,则显而易见
X
X
X 的形状为
(samples, features)
,
y
y
y 的形状为
(samples,)
。
1.1.2 参数
我们通常会作导入:
from sklearn.svm import SVC
使用时只需要
SVC()
即可创建一个SVC实例。
创建一个 SVC 实例常用到以下参数:
S
V
C
(
C
=
1.0
,
k
e
r
n
e
l
=
‘
r
b
f
’
,
d
e
g
r
e
e
=
3
,
g
a
m
m
a
=
‘
s
c
a
l
e
’
,
c
o
e
f
0
=
0.0
,
d
e
c
i
s
i
o
n
_
f
u
n
c
t
i
o
n
_
s
h
a
p
e
=
‘
o
v
r
’
,
r
a
n
d
o
m
_
s
t
a
t
e
=
N
o
n
e
)
\small \begin{aligned} &\mathrm{SVC(C=1.0, kernel=‘rbf’, degree=3,gamma=‘scale’,coef0=0.0,} \\ & \qquad\quad\!\!\!\,\!\;\! \mathrm{decision\_function\_shape=‘ovr’, random\_state=None)} \\ \end{aligned}
SVC(C=1.0,kernel=‘rbf’,degree=3,gamma=‘scale’,coef0=0.0,decision_function_shape=‘ovr’,random_state=None)
C
:
\textcolor{blue}{\mathrm{C:}}
C:
C 是正则化项,必须为正数,默认值为 1。
k
e
r
n
e
l
:
\textcolor{blue}{\mathrm{kernel:}}
kernel:
kernel 是核函数,默认为高斯核。
常见的四种核函数:
- 线性核: ⟨ x , x ′ ⟩ \langle x,x'\rangle ⟨x,x′⟩
- 多项式核: ( γ ⟨ x , x ′ ⟩ + r ) d (\gamma\langle x,x'\rangle+r)^d (γ⟨x,x′⟩+r)d,其中 d d d 是
degree, r r r 是coef0 - 高斯核(RBF核): exp ( − γ ∥ x − x ′ ∥ 2 ) \exp(-\gamma\Vert x-x'\Vert^2) exp(−γ∥x−x′∥2),其中 γ \gamma γ 是
gamma,且必须为正 - Sigmoid核: tanh ( γ ⟨ x , x ′ ⟩ + r ) \tanh(\gamma\langle x,x'\rangle+r) tanh(γ⟨x,x′⟩+r),其中 r r r 是
coef0
这些核函数分别对应:‘linear’、‘poly’、‘rbf’、‘sigmoid’。
d
e
g
r
e
e
:
\textcolor{blue}{\mathrm{degree:}}
degree:
degree 是多项式核中的度数
d
d
d,默认值为
3
3
3,必须是整数。
g
a
m
m
a
:
\textcolor{blue}{\mathrm{gamma:}}
gamma:
gamma 的值可以事先人为给定,它的默认值是 ‘scale’,即
1
f
e
a
t
u
r
e
s
⋅
X
.
v
a
r
(
)
\frac{1}{\mathrm{features}\,\cdot\, X.\mathrm{var()} }
features⋅X.var()1
也可以选择 ‘auto’,此时 gamma 为
1 / features
。
c
o
e
f
0
:
\textcolor{blue}{\mathrm{coef0:}}
coef0:
coef0 是多项式核或Sigmoid核中的系数
r
r
r,默认值为0。
d
e
c
i
s
i
o
n
_
f
u
n
c
t
i
o
n
_
s
h
a
p
e
:
\textcolor{blue}{\mathrm{decision\_function\_shape:}}
decision_function_shape:
决策函数的数学表达式为:
f
(
x
)
=
w
T
ϕ
(
x
)
+
b
=
∑
i
=
1
n
α
i
y
i
κ
(
x
,
x
i
)
+
b
f(\boldsymbol{x})=\boldsymbol{w}^{\mathrm T}\phi(\boldsymbol{x})+b=\sum_{i=1}^n \alpha_iy_i\kappa(\boldsymbol{x},\boldsymbol{x}_i)+b
f(x)=wTϕ(x)+b=i=1∑nαiyiκ(x,xi)+b
对于一个二分类问题,我们的决策函数作用在
X
X
X 上的结果可以表示为:
d
e
c
i
s
i
o
n
_
f
u
n
c
t
i
o
n
(
X
)
=
[
f
(
x
1
)
f
(
x
2
)
⋮
f
(
x
n
)
]
\mathrm{decision\_function}(X)= \begin{bmatrix} f(\boldsymbol{x}_1) \\ f(\boldsymbol{x}_2)\\ \vdots \\ f(\boldsymbol{x}_n) \\ \end{bmatrix}
decision_function(X)=⎣⎢⎢⎢⎡f(x1)f(x2)⋮f(xn)⎦⎥⎥⎥⎤
它是一个一维数组,形状为
(n,)
。对于多分类问题,设有
N
N
N 个类别,如果我们的拆分策略为
O
v
O
\mathrm{OvO}
OvO,则相应的决策函数为
f
1
,
f
2
,
⋯
,
f
N
(
N
−
1
)
/
2
f_1,f_2,\cdots, f_{N(N-1)/2}
f1,f2,⋯,fN(N−1)/2,从而
d
e
c
i
s
i
o
n
_
f
u
n
c
t
i
o
n
(
X
)
=
[
f
1
(
x
1
)
f
2
(
x
1
)
⋯
f
N
(
N
−
1
)
/
2
(
x
1
)
f
1
(
x
2
)
f
2
(
x
2
)
⋯
f
N
(
N
−
1
)
/
2
(
x
2
)
⋮
⋮
⋮
f
1
(
x
n
)
f
2
(
x
n
)
⋯
f
N
(
N
−
1
)
/
2
(
x
n
)
]
\mathrm{decision\_function}(X)= \begin{bmatrix} f_1(\boldsymbol{x}_1) & f_2(\boldsymbol{x}_1) &\cdots & f_{N(N-1)/2}(\boldsymbol{x}_1) \\ f_1(\boldsymbol{x}_2) & f_2(\boldsymbol{x}_2) &\cdots & f_{N(N-1)/2}(\boldsymbol{x}_2) \\ \vdots & \vdots & & \vdots \\ f_1(\boldsymbol{x}_n) & f_2(\boldsymbol{x}_n) &\cdots & f_{N(N-1)/2}(\boldsymbol{x}_n) \\ \end{bmatrix}
decision_function(X)=⎣⎢⎢⎢⎡f1(x1)f1(x2)⋮f1(xn)f2(x1)f2(x2)⋮f2(xn)⋯⋯⋯fN(N−1)/2(x1)fN(N−1)/2(x2)⋮fN(N−1)/2(xn)⎦⎥⎥⎥⎤
如果拆分策略为
O
v
R
\mathrm{OvR}
OvR,则
d
e
c
i
s
i
o
n
_
f
u
n
c
t
i
o
n
(
X
)
=
[
f
1
(
x
1
)
f
2
(
x
1
)
⋯
f
N
(
x
1
)
f
1
(
x
2
)
f
2
(
x
2
)
⋯
f
N
(
x
2
)
⋮
⋮
⋮
f
1
(
x
n
)
f
2
(
x
n
)
⋯
f
N
(
x
n
)
]
\mathrm{decision\_function}(X)= \begin{bmatrix} f_1(\boldsymbol{x}_1) & f_2(\boldsymbol{x}_1) &\cdots & f_{N}(\boldsymbol{x}_1) \\ f_1(\boldsymbol{x}_2) & f_2(\boldsymbol{x}_2) &\cdots & f_{N}(\boldsymbol{x}_2) \\ \vdots & \vdots & & \vdots \\ f_1(\boldsymbol{x}_n) & f_2(\boldsymbol{x}_n) &\cdots & f_{N}(\boldsymbol{x}_n) \\ \end{bmatrix}
decision_function(X)=⎣⎢⎢⎢⎡f1(x1)f1(x2)⋮f1(xn)f2(x1)f2(x2)⋮f2(xn)⋯⋯⋯fN(x1)fN(x2)⋮fN(xn)⎦⎥⎥⎥⎤
即多分类问题下的
d
e
c
i
s
i
o
n
_
f
u
n
c
t
i
o
n
(
X
)
\mathrm{decision\_function}(X)
decision_function(X) 均是二维数组,且
O v O \mathrm{OvO} OvO 策略下,形状为 ```(n, N(N-1)/2)```O v R \mathrm{OvR} OvR 策略下,形状为 ```(n, N)```
所以我们的
d
e
c
i
s
i
o
n
_
f
u
n
c
t
i
o
n
_
s
h
a
p
e
\mathrm{decision\_function\_shape}
decision_function_shape 就是用来控制多分类问题下
d
e
c
i
s
i
o
n
_
f
u
n
c
t
i
o
n
(
X
)
\mathrm{decision\_function}(X)
decision_function(X) 的形状.
d
e
c
i
s
i
o
n
_
f
u
n
c
t
i
o
n
_
s
h
a
p
e
\mathrm{decision\_function\_shape}
decision_function_shape 有两种取值:‘ovo’ 和 ‘ovr’,且默认值为 ‘ovr’。
做二分类任务时此参数可以忽略。
r
a
n
d
o
m
_
s
t
a
t
e
:
\textcolor{blue}{\mathrm{random\_state:}}
random_state:
相当于随机数种子,默认值为
None
。我们一般会选择将其设置为整数,常用的值有 0 和 42。
对于 random_state 不了解的读者可以进一步参考 stackoverflow。
1.1.3 方法
我们一般将使用
SVC()
创建得到的实例称为
estimator
。
方法作用fit(X, y)拟合SVM模型predict(X)预测样本的类别;X 必须是二维数组decision_function(X)1.1.2节中已经介绍过get_params()获取estimator中的各个参数set_params(**params)params为字典;设置estimator的参数score(X_test, y_test)返回测试集上的分类准确度
接下来通过一个例子讲解以上方法。
考虑最简单的情形:正样本为
(
0
,
1
)
(0,1)
(0,1),负样本为
(
1
,
0
)
(1,0)
(1,0),则无需计算就可得知最大间隔超平面为
x
−
y
=
0
x-y=0
x−y=0,且
(
1
,
0
)
(1,0)
(1,0) 和
(
0
,
1
)
(0,1)
(0,1) 均为支持向量。对于新样本
(
m
,
n
)
(m,n)
(m,n),当
n
>
m
n>m
n>m 时它是正样本,当
n
<
m
n<m
n<m 时它是负样本。
首先创建SVC实例:
from sklearn.svm import SVC
X =[[1,0],[0,1]]
y =[-1,1]
clf = SVC()print(clf.get_params())# {'C': 1.0, 'break_ties': False, 'cache_size': 200, 'class_weight': None, 'coef0': 0.0, # 'decision_function_shape': 'ovr', 'degree': 3, 'gamma': 'scale', 'kernel': 'rbf', 'max_iter': # -1, 'probability': False, 'random_state': None, 'shrinking': True, 'tol': 0.001, # 'verbose': False}
可以看出正则化项太小,并且核为高斯核,接下来进行参数设置:
params ={'C':1000000,'kernel':'linear'}
clf.set_params(**params)print(clf.get_params())# {'C': 1000000, 'break_ties': False, 'cache_size': 200, 'class_weight': None, 'coef0': 0.0, # 'decision_function_shape': 'ovr', 'degree': 3, 'gamma': 'scale', 'kernel': 'linear', # 'max_iter': -1, 'probability': False, 'random_state': None, 'shrinking': True, 'tol': 0.001, # 'verbose': False}
可以看到正则化项与核已经设置完成了。当然我们也可以在创建实例的时候就去设置:
clf = SVC(C=1000000, kernel='linear')
之所以绕这么远是为了给读者展示各类方法的使用。
在实例创建完并且参数也都设置好的情况下,就可以进行拟合了:
clf.fit(X, y)
我们可以利用已知条件生成测试集
X_test =[]
y_test =[]for i inrange(2,5):for j inrange(2,5):if j != i:
y_test.append(1if j > i else-1)
X_test.append([i, j])print(X_test)print(y_test)# [[2, 3], [2, 4], [3, 2], [3, 4], [4, 2], [4, 3]]# [1, 1, -1, 1, -1, -1]
然后在测试集上做预测
print(clf.predict(X_test))# [ 1 1 -1 1 -1 -1]
从这里就已经可以看出我们的分类准确率为 100%,这里用 score 函数检验一下:
print(clf.score(X_test, y_test))# 1.0
即分类完全正确。
将决策函数作用在测试集上:
print(clf.decision_function(X_test))# [ 1. 2. -1. 1. -2. -1.]
下面是截止到拟合的完整代码,读者可自行尝试各个方法
from sklearn.svm import SVC
X_test =[]
y_test =[]for i inrange(2,5):for j inrange(2,5):if j != i:
y_test.append(1if j > i else-1)
X_test.append([i, j])
X_train =[[1,0],[0,1]]
y_train =[-1,1]
clf = SVC(C=1000000, kernel='linear')
clf.fit(X_train, y_train)
1.1.4 属性
SVC实例只有在拟合之后才能够使用属性,否则会报错:AttributeError: ‘SVC’ object has no attribute …
有
关
支
持
向
量
\textcolor{green}{有关支持向量}
有关支持向量
属性形态描述support_vectors_数组,形状为
(n_SV, n_features)
支持向量n_support_数组,形状为
(n_classes,)
每个类的支持向量的个数support_数组,形状为
(n_SV,)
支持向量的索引classes_数组,形状为
(n_classes,)
所有类别对应的标签
现在考虑本文一开始提到的二分类问题
from sklearn.svm import SVC
X =[[1,2],[2,3],[3,3],[2,1],[3,2]]
y =[1,1,1,-1,-1]
clf = SVC(C=10**6, kernel='linear')
clf.fit(X, y)
print(clf.support_vectors_)# [[3. 2.]# [1. 2.]# [3. 3.]]print(clf.n_support_)# [1 2]print(clf.support_)# [4 0 2]
从输出结果可以看出,支持向量为
(
3
,
2
)
,
(
1
,
2
)
,
(
3
,
3
)
(3,2), (1,2), (3,3)
(3,2),(1,2),(3,3),它们在
X
X
X 中的索引分别为
4
,
0
,
2
4,0,2
4,0,2。其中,
(
1
,
2
)
,
(
3
,
3
)
(1,2),(3,3)
(1,2),(3,3) 为正样例,
(
3
,
2
)
(3,2)
(3,2) 为负样例,即负样例中有
1
1
1 个支持向量,正样例中有
2
2
2 个支持向量。
可能会有读者疑惑,为什么
clf.n_support_
中是负样例在前而正样例在后呢?事实上,
clf.classes_
返回的是一个有序数组(从小到大排列):
print(clf.classes_)# [-1 1]
而
clf.n_support_
与
clf.classes_
是一个一一对应的关系。因为负样例的标签为
−
1
-1
−1,所以它在
clf.classes_
中的索引便是
0
0
0,故
clf.n_support_
中索引
0
0
0 处对应于负样例中的支持向量的个数。
有
关
决
策
函
数
的
系
数
\textcolor{green}{有关决策函数的系数}
有关决策函数的系数
属性形态描述coef_数组,形状为
(n_classes * (n_classes - 1) / 2, n_features)
当核为线性核时,返回决策函数中的
w
\boldsymbol{w}
wdual_coef_数组,形状为
(n_classes - 1, n_SV)
决策函数中支持向量的系数,即
α
∗
y
\boldsymbol \alpha * \boldsymbol y
α∗y(
∗
*
∗ 是按元素相乘)intercept_数组,形状为
(n_classes * (n_classes - 1) / 2,)
决策函数中的常数,即截距
在二分类的框架下,我们的决策函数为
f
(
x
)
=
w
T
x
+
b
f(\boldsymbol{x})=\boldsymbol{w}^{\mathrm T}\boldsymbol{x}+b
f(x)=wTx+b
为方便写出最大间隔超平面,可以认为
x
=
(
x
1
,
x
2
)
T
=
(
x
,
y
)
T
\boldsymbol{x}=(x_1,x_2)^{\mathrm{T}}=(x,y)^{\mathrm{T}}
x=(x1,x2)T=(x,y)T。于是上面的表格转化为
属性形态描述coef_数组,形状为
(1, n_features)
w
\boldsymbol w
wdual_coef_数组,形状为
(1, n_SV)
α
∗
y
\boldsymbol \alpha * \boldsymbol y
α∗y(支持向量所对应的,
∗
*
∗ 是按元素相乘)intercept_数组,形状为
(1,)
b
b
b
from sklearn.svm import SVC
X =[[1,2],[2,3],[3,3],[2,1],[3,2]]
y =[1,1,1,-1,-1]
clf = SVC(C=10**6, kernel='linear')
clf.fit(X, y)print(clf.coef_)# [[-1. 2.]]print(clf.intercept_)# [-2.]
从输出可以看出,
w
=
(
−
1
,
2
)
T
\boldsymbol{w}=(-1,2)^{\mathrm T}
w=(−1,2)T,
b
=
−
2
b=-2
b=−2,于是最大间隔超平面为
(
−
1
,
2
)
(
x
y
)
−
2
=
0
⇒
−
x
+
2
y
−
2
=
0
⇒
y
=
1
2
x
+
1
(-1,2)\begin{pmatrix} x \\ y \end{pmatrix} -2=0\;\Rightarrow\; -x+2y-2=0\;\Rightarrow\;y=\frac12 x+1
(−1,2)(xy)−2=0⇒−x+2y−2=0⇒y=21x+1
print(clf.dual_coef_)# [[-2.5 0.5 2. ]]
因为对于非支持向量,它对应的
α
i
=
0
\alpha_i=0
αi=0,不会对最终的模型有任何影响,因此
clf.dual_coef_
实际上返回的是支持向量所对应的
α
∗
y
\boldsymbol \alpha * \boldsymbol y
α∗y,由上可知,
α
∗
y
=
(
−
2.5
,
0.5
,
2
)
\boldsymbol \alpha * \boldsymbol y=(-2.5,0.5,2)
α∗y=(−2.5,0.5,2),我们用下面的公式来验证:
w
=
∑
i
∈
S
V
α
i
y
i
x
i
\boldsymbol w=\sum_{i\in SV} \alpha_iy_i\boldsymbol{x}_i
w=i∈SV∑αiyixi
w = np.sum(clf.dual_coef_.T * clf.support_vectors_, axis=0)print(w)# [-1. 2.]
现在考虑多分类的情形,无论采取哪种拆分策略,我们都会训练
K
K
K 个二分类器:
f
1
,
⋯
,
f
K
f_1,\cdots, f_K
f1,⋯,fK:
f
i
(
x
)
=
w
i
T
ϕ
(
x
)
+
b
i
,
i
=
1
,
⋯
,
K
f_i(\boldsymbol x)=\boldsymbol{w}_i^{\mathrm T} \phi(\boldsymbol x)+b_i,\quad i=1,\cdots, K
fi(x)=wiTϕ(x)+bi,i=1,⋯,K
因此
coef_
实际上就是
[
w
1
,
⋯
,
w
K
]
[\boldsymbol w_1,\cdots,\boldsymbol w_K]
[w1,⋯,wK],而
intercept_
实际上就是
[
b
1
,
⋯
,
b
K
]
[b_1,\cdots,b_K]
[b1,⋯,bK],而对于
dual_coef_
,情形就略微复杂了,这里不再讨论,有兴趣的读者可自行参阅官方文档。
1.2 数据可视化
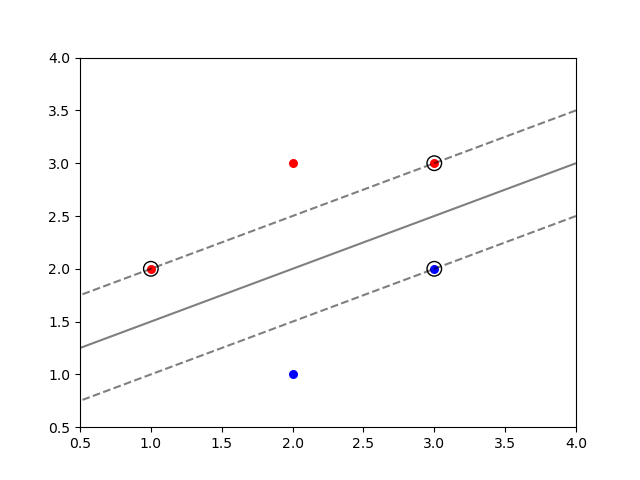
1.1节中我们详细介绍了SVC类的使用方法,并且求解了本文一开始提到的二分类问题。这一小节中,我们会将之前得到的结果可视化,以便进一步理解。
数据(散点)和支持向量(外加黑色圆圈)都可以用
scatter
函数轻松解决,那么该如何绘制分类超平面和边界呢?
注意到超平面的方程和两个边界的方程实际上就是
f
(
x
)
=
0
,
f
(
x
)
=
±
1
f(\boldsymbol{x})=0,\quad f(\boldsymbol{x})=\pm 1
f(x)=0,f(x)=±1
因此我们可以先生成网格点,若其中的某点
x
i
\boldsymbol{x}_i
xi 满足
f
(
x
i
)
=
0
f(\boldsymbol{x}_i)=0
f(xi)=0,则它位于超平面上;若其中的某点
x
i
\boldsymbol{x}_i
xi 满足
f
(
x
i
)
=
±
1
f(\boldsymbol{x}_i)=\pm1
f(xi)=±1,则它位于边界上。
利用此特征,我们可以使用等高线函数
contour
来绘制。
from sklearn.svm import SVC
import numpy as np
import matplotlib.pyplot as plt
# 初始化与拟合
X = np.array([[1,2],[2,3],[3,3],[2,1],[3,2]])
y = np.array([1,1,1,-1,-1])
clf = SVC(C=10**6, kernel='linear')
clf.fit(X, y)# 绘制数据
plt.scatter(X[:3][:,0], X[:3][:,1], s=30, c='r')
plt.scatter(X[3:][:,0], X[3:][:,1], s=30, c='b')
plt.xlim((0.5,4))
plt.ylim((0.5,4))
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()# 绘制最大间隔超平面和边界
xx = np.linspace(xlim[0], xlim[1],50)
yy = np.linspace(ylim[0], ylim[1],50)
XX, YY = np.meshgrid(xx, yy)
xy = np.vstack([XX.ravel(), YY.ravel()]).T
Z = clf.decision_function(xy).reshape(XX.shape)
ax.contour(XX, YY, Z, colors="k", levels=[-1,0,1], alpha=0.5, linestyles=["--","-","--"])# 绘制支持向量
ax.scatter(
clf.support_vectors_[:,0],
clf.support_vectors_[:,1],
s=110,
linewidth=1,
facecolors="none",
edgecolors="k",)
plt.show()
二、软间隔SVM
第一章节中我们所实现的 “硬间隔SVM” 实际上就是软间隔SVM,因为 sklearn 中没有硬间隔SVM,所以我们只能把
C
C
C 设置的充分大来模拟硬间隔SVM。
在这一章节中,我们会将
C
C
C 设置的较小并且采用不同的核函数来观察效果。
2.1 sklearn.datasets.make_blobs()
我们通常会作导入:
from sklearn.datasets import make_blobs
正如其名,该函数可以用来方便快捷地生成斑点数据集,其常用的参数如下:
m
a
k
e
_
b
l
o
b
s
(
n
_
s
a
m
p
l
e
s
=
100
,
n
_
f
e
a
t
u
r
e
s
=
2
,
c
e
n
t
e
r
s
=
N
o
n
e
,
r
a
n
d
o
m
_
s
t
a
t
e
=
N
o
n
e
)
\mathrm{make\_blobs(n\_samples=100, n\_features=2, centers=None, random\_state=None)}
make_blobs(n_samples=100,n_features=2,centers=None,random_state=None)
参数描述n_samples控制样本(斑点)个数;默认值为100n_features控制样本的特征数;默认值为2,即样本处于二维空间centers决定样本有多少种类别;对于二分类问题可将其设置为2
该函数会返回列表
[X, y]
,我们只需要用两个参数
X
,
y
X, y
X,y 去接收即可。
X, y = make_blobs(n_features=2, centers=2, random_state=33)
plt.scatter(X[:,0], X[:,1], c=y)
plt.show()

从上图可以看出,我们找不到一个能将两类样本完全分开的超平面,因此就必须允许SVM在某些样本上出错,即软间隔SVM。
2.2 数据可视化
接下来我们只绘制超平面和边界,不再绘制支持向量,且除了核函数之外全部使用默认参数。
首先采用线性核,完整的代码如下:
from sklearn.svm import SVC
from sklearn.datasets import make_blobs
import numpy as np
import matplotlib.pyplot as plt
X, y = make_blobs(n_features=2, centers=2, random_state=33)
clf = SVC(kernel='linear')
clf.fit(X, y)
plt.scatter(X[:,0], X[:,1], c=y)
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()
xx = np.linspace(xlim[0], xlim[1],50)
yy = np.linspace(ylim[0], ylim[1],50)
XX, YY = np.meshgrid(xx, yy)
xy = np.vstack([XX.ravel(), YY.ravel()]).T
Z = clf.decision_function(xy).reshape(XX.shape)
ax.contour(XX, YY, Z, colors="k", levels=[-1,0,1], alpha=0.5, linestyles=["--","-","--"])
plt.show()
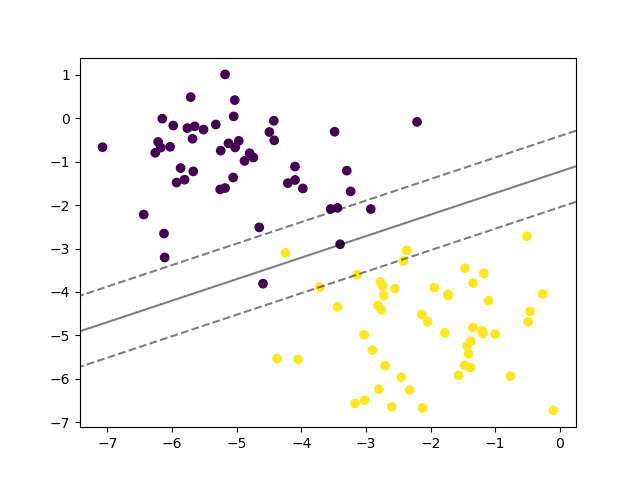
采用高斯核,即
clf = SVC()

采用多项式核
clf = SVC(kernel='poly')
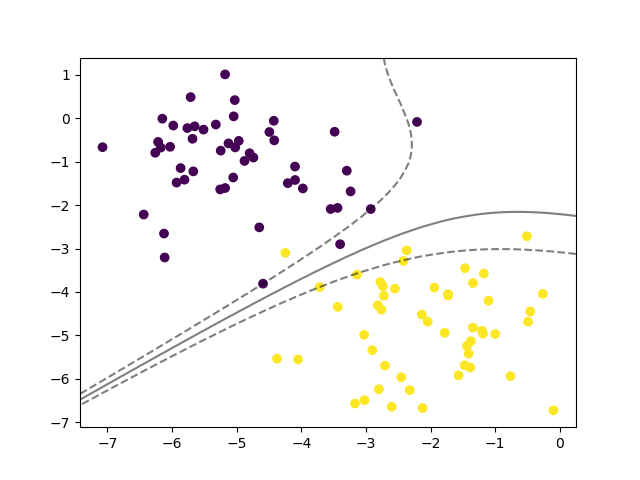
采用Sigmoid核
clf = SVC(kernel='sigmoid')
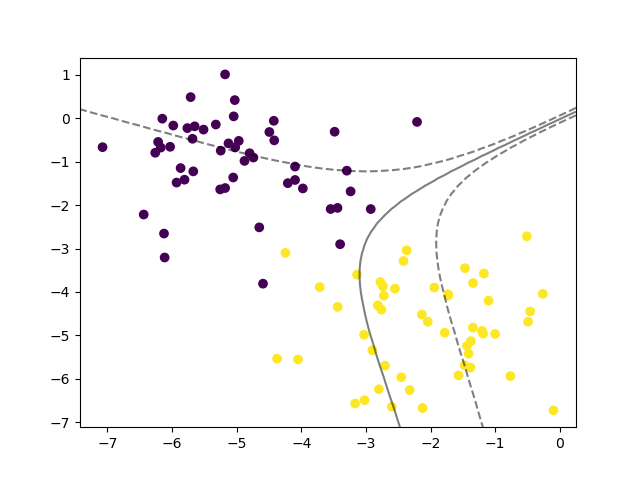
直观来讲,采用Sigmoid核训练得到的SVM的分类效果是最差的。
版权归原作者 serity 所有, 如有侵权,请联系我们删除。