一、BN层的由来
训练深度学习网络是一个相当复杂的过程,每个层的输入分布在训练中会随着前一层的参数变化而变化。使用更好的参数初始化或者使用较低的分辨率能够一定程度上缓和这个问题,但是会降低网络的训练速度,特别是具有饱和非线性的网络。在论文中被称为Internal covariate shift,为了解决这个问题,提出了BN层。
二、BN层的作用
Internal covariate shift是BN论文作者提出的概念,表示数据的分布在网络传播过程中会发生偏移。举个例子,假设有一个玫瑰花的分类网络,1表示识别为玫瑰花,0表示非玫瑰花。先看看训练数据集的一个mini_batch:
直观来说,玫瑰花的特征表现很明显,都是红色玫瑰花。 再看看训练数据集的另一部分:
很明显,第二张图中各个颜色的玫瑰花都有,其特征分布与第一张图的特征分布是不一样的。
通俗来讲,刚开始的数据都是同一分布的,在模型学习的过程中,模型的参数已经适应了一种分布,突然换了另一种分布,这就会让模型的参数发生很大的调整,从而影响到收敛速度和精度,这就是Internal covariate shift。
而BN层的作用就是将这些输入值或卷积神经网络的张量进行类似标准化的操作,将其缩放在合适的范围,从而加快训练速度;另一方面可以使得每一层可以尽量面对同一特征分布的输入值,减少了变化带来的不确定性。
具体
1.加快网络的训练和收敛速度
2. 控制梯度爆炸和梯度消失
3. 防止过拟合
分析
(1)加快收敛速度:在深度神经网络中,如果每一层的数据分布都不一样的话,将会导致网络非常难收敛和训练,而如果把每层的数据都转换为均值为0,方差为1的分布下,这样每层数据的分布都是一样的,训练比较容易收敛。
(2)防止梯度爆炸和梯度消失:以sigmoid函数为例子,上一篇介绍了网络在训练时使用的激活函数,sigmoid函数可以使得输出在[0,1]之间。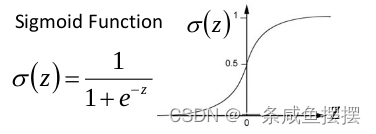
事实上,当x到达了一定的大小,经过sigmo函数的输出范围就很小了,参考下图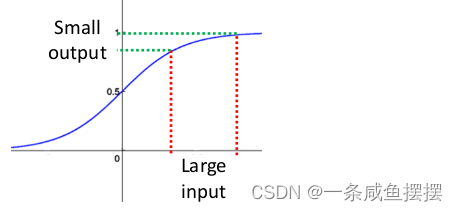
可以看出,如果输入很大,其斜率会变得越来越小,而斜率(梯度)在反向传播中时权值的学习速率,所以就会出现下面的问题: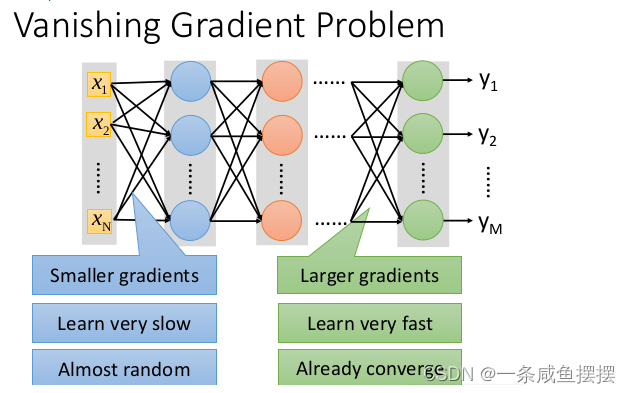
在深度学习网络中,如果网络的激活输出很大,其梯度就很小,学习速率就很慢。假设每层学习梯度都小于最大值0.25,网络有n层,因为链式求导的原因,第一层的梯度小于0.25的n次方,所以学习速率就慢,对于最后一层只需对自身求导一次,梯度就很大,学习速率就快。
因此就会造成在一个很深的网络中,浅层特征基本不学习,权值变化小,后面几层一直在学习,结果就是后面几层基本可以表示整个网络,失去了深度的意义。
对于梯度爆炸,根据链式求导法,第一层偏移量的梯度=激活层斜率1x权值1x激活层斜率2x…激活层斜率(n-1)x权值(n-1)x激活层斜率n。
假如激活层斜率均为最大值0.25,所有层的权值为100,这样梯度就会指数增加。
三、BN层的操作
假设某一个batch的数据为2个2行2列2深度的张量,BN的过程如下: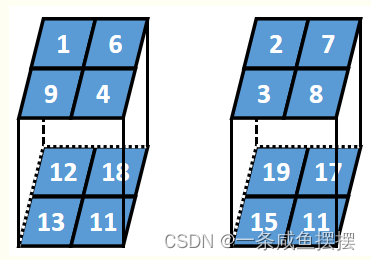
第一步,计算每一层深度的均值和方差: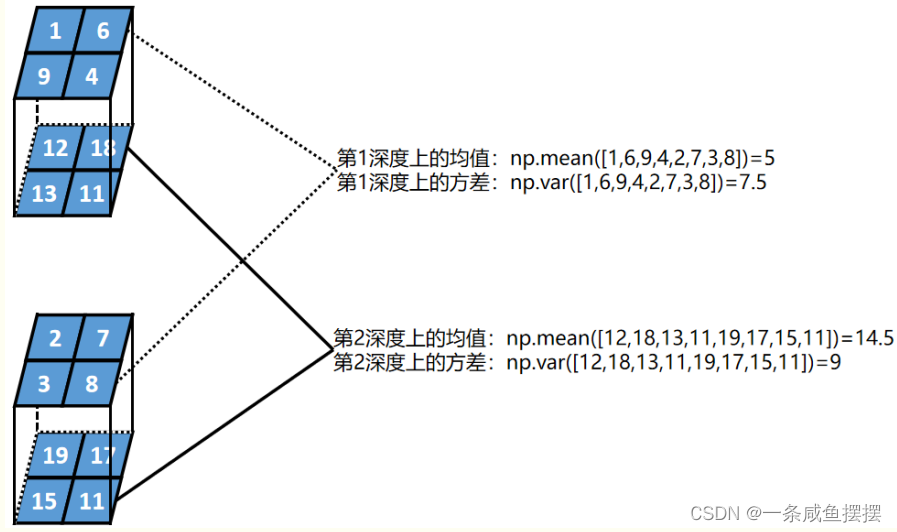
第二步,对每一层设置2个参数,γ和β。假设第1深度γ=2、β=3;第2深度γ=5、β=8。
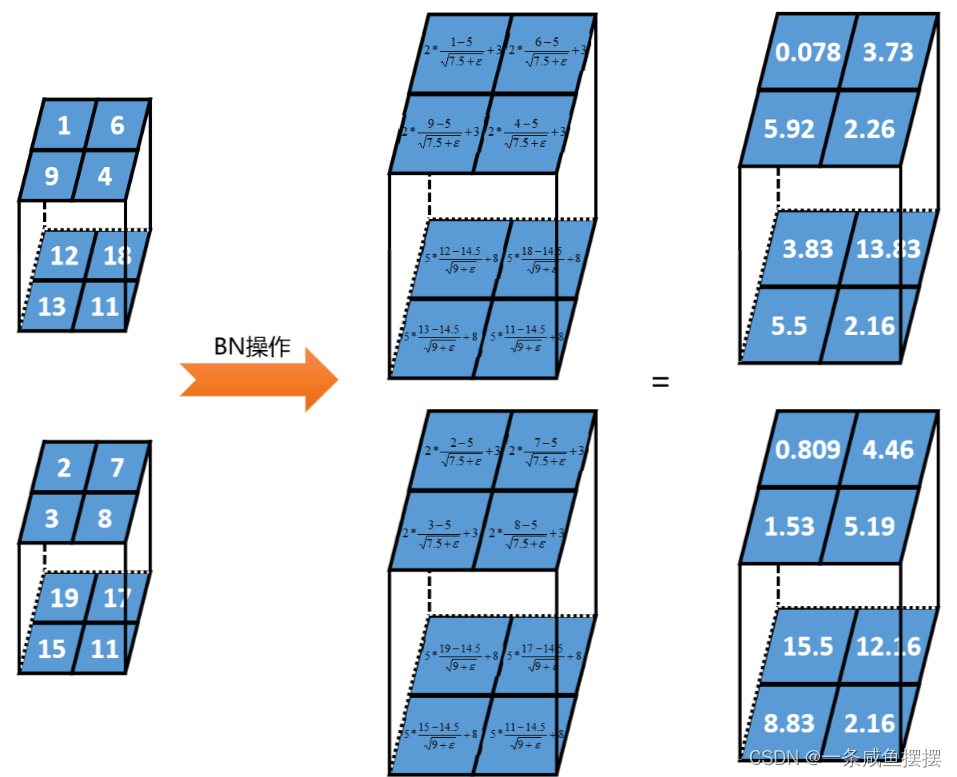
四、测试阶段的BN层
测试的时候如果按照训练那样计算每一个batch的均值和方差来计算BN层的输出的话,假设测试的batch为1,那么对模型的泛化能力会大大降低。这里借用一句话:某一个样本经过测试时应该有确定的输出,如果在测试时也是用测试数据的means和var,那么样本的输出会随所处batch的不同,而有所差异。即batch的随机性导致了样本测试的不确定性。所以使用固定的在训练中得出的mean和var。因此,单个样本的输出不应取决于批量归⼀化所需要的随机小批量中的均值和⽅差。这句话其实就是说为了增加模型的鲁棒性,在测试的时候使用的均值和方差为训练数据通过指数滑动平均(ExponentialMovingAverage)EMA估算整个训练数据集的样本均值和方差的全局值,并不是当前测试batch的局部值。
五、为什么BN层一般用在线性层和卷积层的后面,而不是放在激活函数后
因此激活函数一般为非线性,非线性单元的输出分布形状会在训练过程中发生变化,归一化无法消除它的方差偏移,相反的,全连接和卷积层的输出一般是一个对称的,非稀疏的一个分布,更加类似于高斯分布,对他们进行归一化会产生更加稳定的分布。例如Relu激活函数,如果输入的数据是一个高斯分布,经过Relu输出的数据小于0的被抑制,就不是高斯分布了。
参考链接:
1.卷积神经网络CNN(2)—— BN(Batch Normalization) 原理与使用过程详解
2.https://www.cnblogs.com/itmorn/p/11241236.html
3.网络中BN层的作用
版权归原作者 一条咸鱼摆摆 所有, 如有侵权,请联系我们删除。