排序（一）——简单排序：插入排序 && 冒泡排序

相关文章：

• 排序（二）：分而治之——快速排序 && 归并排序
• 排序（三）：谁主沉浮——堆与堆排序

leetcode：https://leetcode-cn.com/problems/sort-an-array/

插入排序

过程

插入排序的过程分为两步：

• 首先和当前位置的前一个元素进行比较，如果前一个元素比当前元素大，则后续进行调整，将前面的大元素不断向后移动，并找到合适的位置将当前元素插入进去；
• 如果发现前一个元素比当前元素小，则不会进行调整，默认前面的元素已经有序。

示意图如下：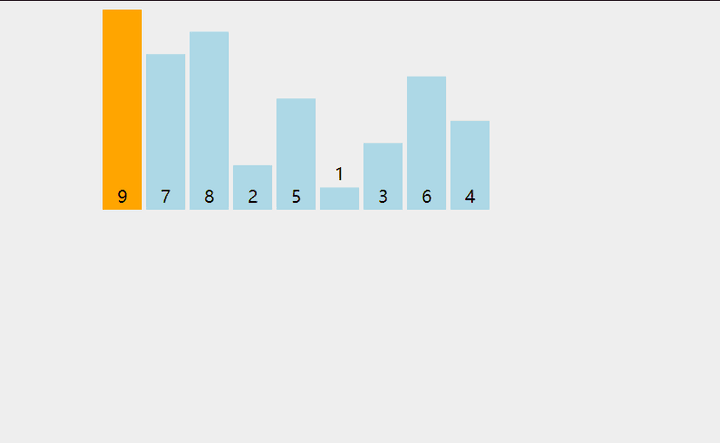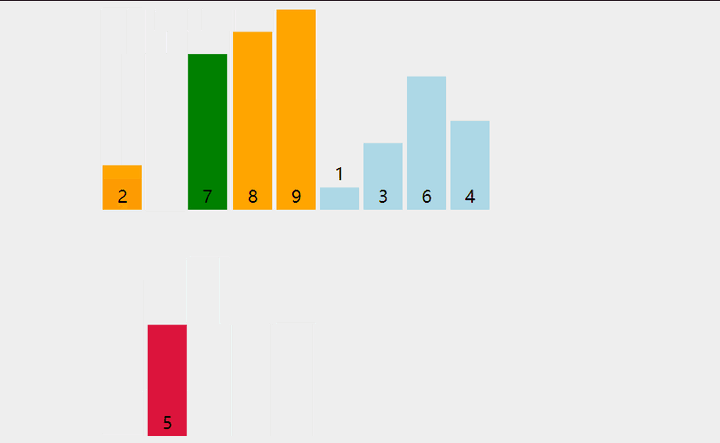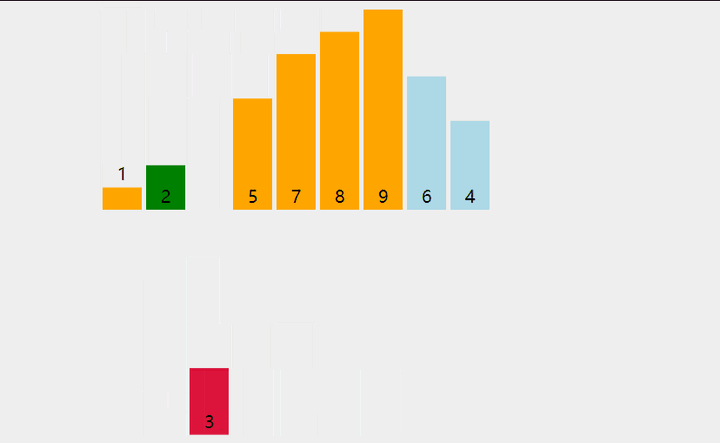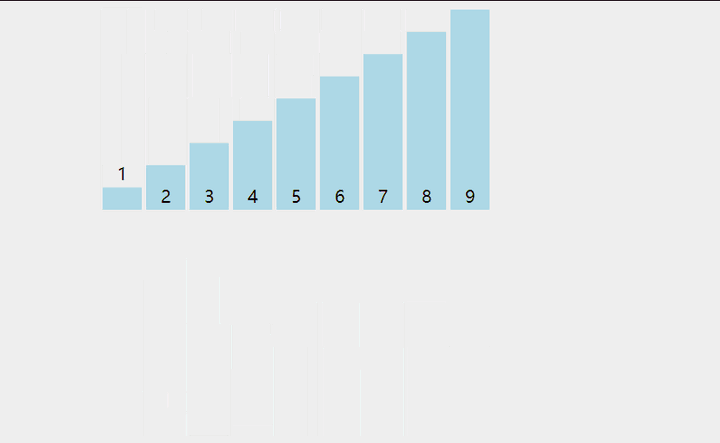

插入排序的特点是：基于比较、数据移动完成排序，一次比较操作后不发生数据移动或仅仅交换一对相邻的数据元素。

代码

classSolution{publicint[]sortArray(int[] nums){int i,j;for(i =1; i < nums.length; i++){if(nums[i]< nums[i-1]){int temp = nums[i];
                nums[i]= nums[i-1];for(j = i-2; j >=0&& nums[j]> temp; j--){
                    nums[j+1]= nums[j];}
                nums[j+1]= temp;}}return nums;}}

时间复杂度

逆序：对于数对

    (
   
   
    π
   
   
    (
   
   
    i
   
   
    )
   
   
    ,
   
   
    π
   
   
    (
   
   
    j
   
   
    )
   
   
    )
   
  
  
   (\pi(i), \pi(j))
  
 
(π(i),π(j)) ，有 

 
  
   
    j
   
   
    <
   
   
    j
   
  
  
   j < j
  
 
j<j 而 

 
  
   
    π
   
   
    (
   
   
    i
   
   
    )
   
   
    >
   
   
    π
   
   
    (
   
   
    j
   
   
    )
   
  
  
   \pi(i)>\pi(j)
  
 
π(i)>π(j) 。

插入排序的实质是消除数对的逆序，一个含有 n 个元素的序列有

      n
     
     
      (
     
     
      n
     
     
      −
     
     
      1
     
     
      )
     
    
    
     2
    
   
  
  
   \frac{n(n-1)}{2}
  
 
2n(n−1)​ 个数对，则最多有 

 
  
   
    
     
      n
     
     
      (
     
     
      n
     
     
      −
     
     
      1
     
     
      )
     
    
    
     2
    
   
  
  
   \frac{n(n-1)}{2}
  
 
2n(n−1)​ 个逆序，平均有 

 
  
   
    
     
      n
     
     
      (
     
     
      n
     
     
      −
     
     
      1
     
     
      )
     
    
    
     4
    
   
  
  
   \frac{n(n-1)}{4}
  
 
4n(n−1)​ 个逆序，而插入排序在一次数对比较之后最后消除一对逆序。

基于此，分析插入排序的最好情况

    B
   
   
    (
   
   
    n
   
   
    )
   
  
  
   B(n)
  
 
B(n)，平均情况 

 
  
   
    A
   
   
    (
   
   
    n
   
   
    )
   
  
  
   A(n)
  
 
A(n) 和最坏情况 

 
  
   
    W
   
   
    (
   
   
    n
   
   
    )
   
  
  
   W(n)
  
 
W(n)。

• 最好情况：元素升序有序。那么我们只需要进行 n-1 次元素比较，0 次元素移动即可， B ( n ) ∈ O ( n ) B(n) \in O(n) B(n)∈O(n)。
• 最坏情况：元素降序有序。那么我们需要进行 n ( n − 1 ) 2 \frac{n(n-1)}{2} 2n(n−1)​ 次元素比较，同样次数的元素移动， W ( n ) ∈ O ( n 2 ) W(n) \displaystyle \in O(n^2) W(n)∈O(n2)。
• 平均时间复杂度：平均比较 n ( n − 1 ) 4 \frac{n(n-1)}{4} 4n(n−1)​ 次， A ( n ) ∈ O ( n 2 ) A(n) \displaystyle \in O(n^2) A(n)∈O(n2)。

代码优化

定理：任何一个基于关键字的比较且每一次比较最多消除一个逆序的排序算法，最坏的情况下至少比较

      n
     
     
      (
     
     
      n
     
     
      −
     
     
      1
     
     
      )
     
    
    
     2
    
   
  
  
   \frac{n(n-1)}{2}
  
 
2n(n−1)​ 次，平均情况至少比较 

 
  
   
    
     
      n
     
     
      (
     
     
      n
     
     
      −
     
     
      1
     
     
      )
     
    
    
     4
    
   
  
  
   \frac{n(n-1)}{4}
  
 
4n(n−1)​ 次。无法从 

 
  
   
    O
   
   
    (
   
   
    
     n
    
    
     2
    
   
   
    )
   
  
  
   O(n^2)
  
 
O(n2) 的复杂度降低。

冒泡排序

过程

• 将待排序的数据元素的关键字顺次两两比较，若为逆序则将两个数据元素交换
• 将待排序的数据元素照此方法从头到尾处理一遍称作一趟起泡排序，它将关键字值最大的数据元素交换到排序的最终位置。
• 对含 n 个记录的文件排序最多需要 n-1 趟冒泡排序。

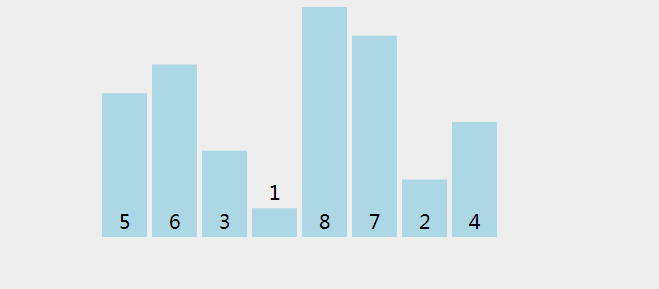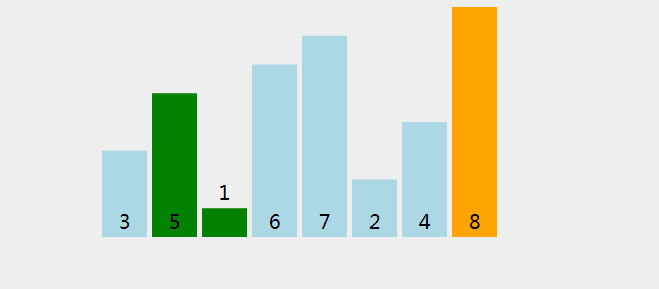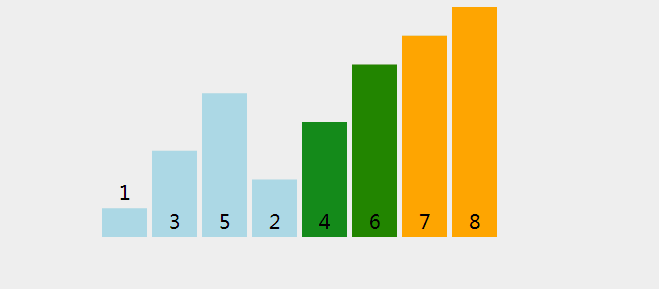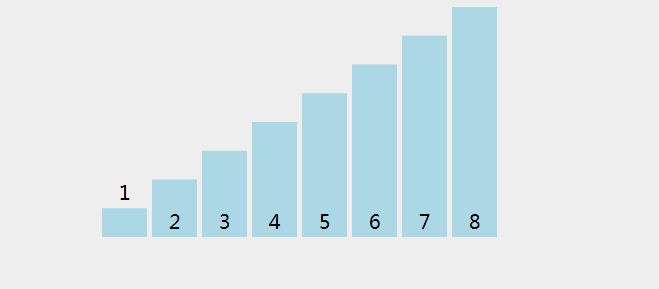
代码

classSolution{publicint[]sortArray(int[] nums){for(int i =0; i < nums.length; i++){for(int j =0; j < nums.length-i-1; j++){if(nums[j]> nums[j+1]){int temp = nums[j+1];
                    nums[j+1]= nums[j];
                    nums[j]= temp;}}}return nums;}}

时间复杂度

• 最坏情况：序列是逆序，需要比较的次数为 n(n-1)/2，则对应时间复杂度为 $ W(n) \displaystyle \in O(n^2)$ 。
• 最好情况：序列已经是升序有序序列，则进行一次比较即可，第一次比较发现没有发生数据移动，则排序结束，比较次数为 n - 1 次，则时间复杂度为 B ( n ) ∈ O ( n 2 ) ) B(n) \displaystyle \in O(n^2)) B(n)∈O(n2)) 。
• 平均情况： A ( n ) ∈ O ( n 2 ) ) A(n) \displaystyle \in O(n^2)) A(n)∈O(n2))

代码优化

优化1：记下最后一次交换的位置，后边没有交换，必然是有序的，然后下一次排序从第一个比较到上次记录的位置结束即可。同时引入布尔变量 sorted 作为标记，如果在一趟排序中没有交换元素，说明这组数据已经有序，不用再继续下去。

classSolution{publicint[]sortArray(int[] nums){int temp =0;intLastExchangeIndex=0;//上一次交换位置int border = nums.length-1;//无序列表边界for(int i =0; i < nums.length; i++){boolean sorted =true;for(int j =0; j < border; j++){if(nums[j]> nums[j+1]){
                    temp = nums[j+1];
                    nums[j+1]= nums[j];
                    nums[j]= temp;LastExchangeIndex= j;
                    sorted =false;}}if(sorted)break;
            border =LastExchangeIndex;}return nums;}}

优化2：双边界冒泡排序，见《计算机算法——设计与分析导论》习题4.5。以序列(2,3,4,5,1) 为例，在普通冒泡排序下，需要盲目比较左侧有序子列，引入左侧边界解决这一问题：找到首个交换位置 pos，则下一趟冒泡排序的起始位置 border_left = pos - 1 or 0。

classSolution{publicint[]sortArray(int[] nums){//双边界冒泡排序intFirstExchangeIndex=0;intLastExchangeIndex=0;int border_left =0;int border_right = nums.length -1;for(int i =0; i < nums.length; i++){boolean sorted_left =true;boolean sorted =true;for(int j = border_left; j < border_right; j++){if(nums[j]> nums[j+1]){//记录首个交换的位置if(sorted_left){
                        border_left = j-1>=0? j-1:0;//左边界更新
                        sorted_left =false;}int temp = nums[j];
                    nums[j]= nums[j+1];
                    nums[j+1]= temp;
                    sorted =false;LastExchangeIndex= j;}}if(sorted)break;
            border_right =LastExchangeIndex;}return nums;}}

优化3：鸡尾酒排序，又称双向冒泡排序、搅拌排序。排序过程像钟摆一样，奇数轮从左到右，偶数轮从右到左。示意图如下：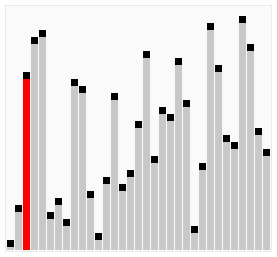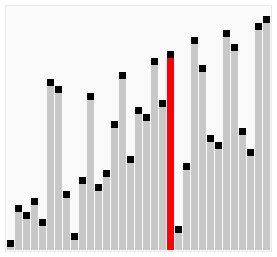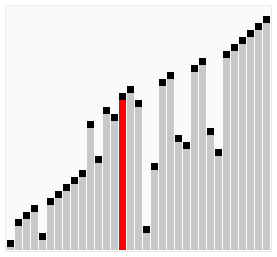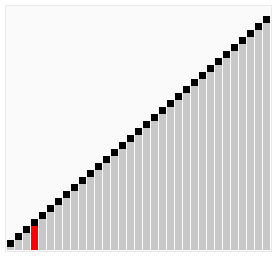

鸡尾酒排序适用于基本有序的序列。还以序列(2,3,4,5,1)为例，鸡尾酒排序只需要访问一次序列就可以完成排序，但如果使用冒泡排序则需要四次。在乱数序列的状态下，鸡尾酒排序与冒泡排序的效率相当（都为

    O
   
   
    (
   
   
    
     n
    
    
     2
    
   
   
    )
   
  
  
   O(n^2)
  
 
O(n2) ）。缺点是代码量较大。

• 最差时间复杂度 O ( n 2 ) O(n^2) O(n2)
• 最优时间复杂度 O ( n ) O(n) O(n)
• 平均时间复杂度 O ( n 2 ) O(n^2) O(n2)

classSolution{publicint[]sortArray(int[] nums){int border_right = nums.length -1;int border_left =0;intLastExchangeIndex_right=0;intLastExchangeIndex_left=0;for(int i =0; i < nums.length/2; i++){//正向boolean sorted =true;for(int j =0; j < border_right; j++){if(nums[j]> nums[j+1]){int temp = nums[j];
                    nums[j]= nums[j+1];
                    nums[j+1]= temp;LastExchangeIndex_right= j;
                    sorted =false;}}if(sorted)break;
            border_right =LastExchangeIndex_right;//反向
            sorted =true;for(int j = nums.length-1-i; j > border_left; j--){if(nums[j]< nums[j-1]){int temp = nums[j];
                    nums[j]= nums[j-1];
                    nums[j-1]= temp;LastExchangeIndex_left= j;
                    sorted =false;}}if(sorted)break;
            border_left =LastExchangeIndex_left;}return nums;}}