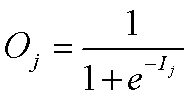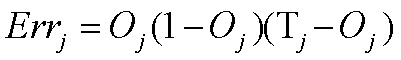数据挖掘(6.1)--神经网络

神经网络简介

神经网络是一种计算模型，它受到人脑处理信息的生物神经网络过程的启发。人工神经网络(ANN)一般也称为神经网络(Neural Network,NN)。

神经网络是由多个神经元组成的，每个神经元都有一个输入和一个输出，它们之间通过权重进行连接。当输入数据经过多个神经元后，输出结果就是由这些神经元的输出加权求和得到的。

BP算法

BP算法(Back Propagation Algorithm)是一种常用的神经网络训练算法，用于在监督学习中对前向传播算法

神经网络是一种计算模型，它受到人脑处理信息的生物神经网络过程的启发。人工神经网络(ANN)一般也称为神经网络(Neural Network,NN)。

神经网络是由多个神经元组成的，每个神经元都有一个输入和一个输出，它们之间通过权重进行连接。当输入数据经过多个神经元后，输出结果就是由这些神经元的输出加权求和得到的。

进行优化。BP算法基于误差反向传播原理，通过计算每个神经元对于输出结果的误差，然后将误差从输出层反向传播到输入层，逐层更新每个神经元的权重和偏置值，以最小化预测结果与真实结果之间的误差。

Delta学习规则的基本原理

Delta学习规则又称梯度法或最速下降法,其要点是改变单元间的连接权重来减小系统实际输出与期望输出间的误差

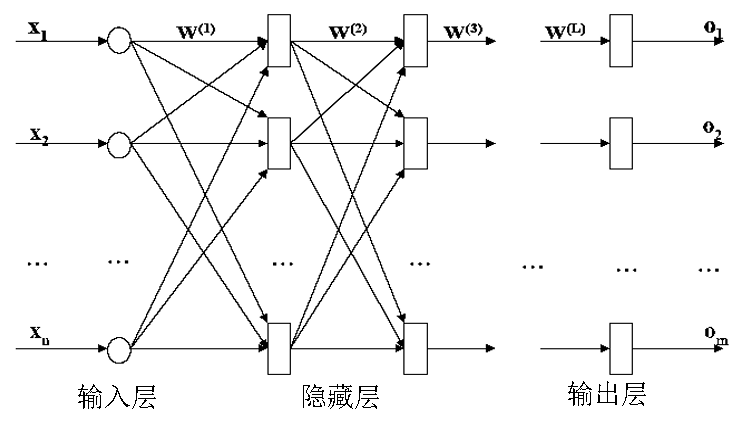
BP神经网络的结构

BP神经网络是具有三层或三层以上的阶层型神经网络，由输入层、隐含层和输出层构成，相邻层之间的神经元全互连，同一层内的神经元无连接

BP神经网络的算法描述

BP算法的主要思想是从后向前(反向)逐层传播输出层的误差，以间接算出隐层误差。

算法分为两个阶段：

第一阶段(正向传播过程)输入信息从输入层经隐层逐层计算各单元的输出值

第二阶段(反向传播过程)输出误差逐层向前算出隐层各单元的误差,并用此误差修正前层权值

具体来说，BP算法包括以下几个步骤：

1. 初始化模型参数(如神经元的权重和偏置值)。
2. 前向传播计算网络的输出结果。
3. 计算网络输出结果与真实结果之间的误差。
4. 根据误差反向传播原理，计算每个神经元对于误差的贡献，并根据梯度下降算法更新每个神经元的权重和偏置值。
5. 重复执行以上步骤，直到达到一定的迭代次数或损失函数收敛。

神经网络训练一般步骤

初始化权重

将输入元组一个一个注入网络

对于每个输入元组，执行如下过程：

①每个单元的经输入计算为这个单元所有输入的线性组合

②使用激活函数计算输出值

③更新权重值和阈值(偏差)

后****向传播算法的主要步骤

①用随机值初始化权重

②向前传播输入，对每个隐含层或输出单元，计算其输入和输出，并最终计算出预测结果

单元j的净输入：

假设一个隐藏或输出单元为j，单元j的输人来自上一层的输出,Wij是由上一层单元i到单元j的连接权重，是上一层单元i的输出，是单元j的偏倚。

单元j的净输出：

③向后传播误差。更新权重和阈值（从输出层开始）

输出层单元j的误差：

隐含层单元j的误差：

其中,是单元j到下一较高层单元k的连接权重，Errk是单元k的误差。

其中是权重的改变;l是学习速率,通常取0.0~1.0之间的常数，一种经验的设置是将学习率设置为1/t ,t是当前训练集迭代的次数。

优缺点

优点

• 非线性映射能力
• 自学习和自适应能力
• 泛化能力
• 容错能力

缺点

• 结构选择不一
• 局部极小化、收敛速度慢
• 预测能力和训练能力的矛盾问题
• 样本依赖性问题

BP算法简单举例

import numpy as np
from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler

# 定义sigmoid函数
def sigmoid(x):
    return 1 / (1 + np.exp(-x))

# 定义BP算法
def backpropagation(X, y, hidden_nodes, output_nodes, learning_rate, epochs):
    # 初始化权重
    input_nodes = X.shape[1]
    hidden_weights = np.random.normal(scale=1 / input_nodes ** 0.5, size=(input_nodes, hidden_nodes))
    output_weights = np.random.normal(scale=1 / hidden_nodes ** 0.5, size=(hidden_nodes, output_nodes))

    # 训练
    for i in range(epochs):
        # 前向传播
        hidden_inputs = np.dot(X, hidden_weights)
        hidden_outputs = sigmoid(hidden_inputs)
        output_inputs = np.dot(hidden_outputs, output_weights)
        output_outputs = sigmoid(output_inputs)

        # 计算误差
        output_error = y - output_outputs
        output_delta = output_error * output_outputs * (1 - output_outputs)

        hidden_error = np.dot(output_delta, output_weights.T)
        hidden_delta = hidden_error * hidden_outputs * (1 - hidden_outputs)

        # 更新权重
        output_weights += learning_rate * np.dot(hidden_outputs.T, output_delta)
        hidden_weights += learning_rate * np.dot(X.T, hidden_delta)

    return output_outputs

# 加载数据集
iris = load_iris()
X = iris.data
y = iris.target

# 数据预处理
scaler = StandardScaler()
X = scaler.fit_transform(X)
# 将标签转换为one-hot编码
y_onehot = np.zeros((y.size, y.max()+1))
y_onehot[np.arange(y.size), y] = 1

# 训练模型
output = backpropagation(X, y_onehot, hidden_nodes=5, output_nodes=3, learning_rate=0.1, epochs=10000)

# 预测结果
y_pred = np.argmax(output, axis=1)

# 计算准确率
accuracy = np.mean(y_pred == y)
print('Accuracy:', accuracy)

输出结果：

Accuracy: 0.9933333333333333