0
0

Vision Transformer中的图像块嵌入详解：线性投影和二维卷积的数学原理与代码实现

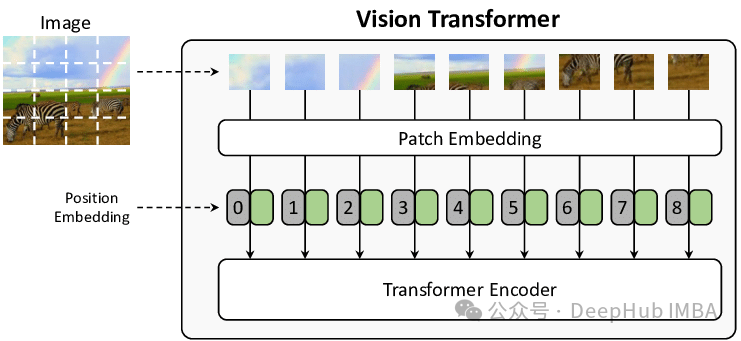
Transformer 架构因其强大的通用性而备受瞩目，它能够处理文本、图像或任何类型的数据及其组合。其核心的“Attention”机制通过计算序列中每个 token 之间的自相似性，从而实现对各种类型数据的总结和生成。在 Vision Transformer 中，图像首先被分解为正方形图像块，然后将这些图像块展平为单个向量嵌入。这些嵌入可以被视为与文本嵌入（或任何其他嵌入）完全相同，甚至可以与其他数据类型进行连接。通常图像块的创建步骤会与使用 2D 卷积的第一个可学习的非线性变换相结合，这对于初学者来说可能比较难以理解，所以本文将深入探讨这一过程。

数据准备

为了简单起见，本文使用 MNIST 数据集，这是一个手写数字的集合，常用于训练基本的图像分类器。MNIST 图像在 PyTorch 中可以直接获取，并且可以使用 

  1. DataLoader

类方便地加载：

  1.  from torchvision.datasets.mnist import MNIST
  2. from torch.utils.data import DataLoader
  3. import torchvision.transforms as T
  4. import torch
  6. torch.manual_seed(42)
  8. img_size = (32,32) #我们将把 MNIST 图像调整为这个大小
  9. batch_size = 4
  11. transform = T.Compose([
  12.   T.ToTensor(),
  13.   T.Resize(img_size)
  14. ])
  16. train_set = MNIST(
  17.   root="./../datasets", train=True, download=True, transform=transform
  18.   )
  20. train_loader = DataLoader(train_set, shuffle=True, batch_size=batch_size)
  22.  batch = next(iter(train_loader)) #加载第一个批次

上述代码首先下载 MNIST 数据集，然后定义一个 PyTorch 变换，该变换将图像转换为 PyTorch 张量并将其大小调整为 32x32。接着，使用 

  1. DataLoader

类加载一个大小为 batch_size = 4 的图像批次。

  1. torch.manual_seed

函数用于将随机数生成器初始化为相同的值，以确保读者在自己的 notebook 中能够看到与本文中相同的图像。有关 PyTorch 的 

  1. DataSet

和 

  1. DataLoader

类的更多信息，请参考以下链接：

可以使用 matplotlib 可视化该批次，其中包含四个图像和对应的四个标签：

  1.  import matplotlib.pyplot as plt
  3. #batch[0] 包含图像，batch[1] 包含标签
  4. images = batch[0]
  5. labels = batch[1]
  7. #为子图创建一个图形和轴
  8. fig, axes = plt.subplots(1, batch_size, figsize=(12, 4))
  10. #迭代图像和标签的批次
  11. for i in range(batch_size):
  12.   #将图像张量转换为 NumPy 数组，如果它是灰度图像，则删除通道维度
  13.   image_np = images[i].numpy().squeeze()
  15.   #在相应的子图中显示图像
  16.   axes[i].imshow(image_np, cmap='gray')  #对灰度图像使用 'gray' cmap
  17.   axes[i].set_title(f"Class: {labels[i].item()}") #假设标签是张量，使用 .item() 获取值
  18.   axes[i].axis('off')
  20. # 调整子图之间的间距
  21. plt.tight_layout()
  23. #显示绘图
  24.  plt.show()

上图展示了使用上述代码生成的四个随机 MNIST 图像。

图像块的创建

使用 Transformer 神经网络处理图像的第一步是将其分解为图像块。例如，可以将 32x32 的图像分解为 64 个 4x4 的图像块（每个块包含 16 个像素）、16 个 8x8 的图像块（每个块包含 64 个像素）或 4 个 16x16 的图像块（每个块包含 256 个像素）：

上图分别展示了 64 个 4x4 图像块、16 个 8x8 图像块和 4 个 16x16 图像块。

虽然我们以二维形式展示这些图像块，但也可以将它们存储在维度分别为 16、64 或 256 的列向量中。这些向量嵌入与文本嵌入已经没有本质区别，它们的序列可以被视为与字符串或单词的序列相同。有关 Transformer 架构的更多信息，可以参考以下链接，其中使用文本嵌入作为示例进行了详细讲解：

以下是使用 PyTorch 的 

  1. unfold

算子分解图像的代码：

  1.  import torch
  2. import torch.nn as nn
  3. import matplotlib.pyplot as plt
  4. import numpy as np
  6. # 图像和块大小
  7. img_size = (32, 32)
  8. patch_size = (8, 8)
  9. n_channels = 1
  11. image = batch[0][1].unsqueeze(0)
  13. #块类
  14. class Patch(nn.Module):
  15.     def __init__(self, img_size, patch_size, n_channels):
  16.         super().__init__()
  17.         self.patch_size = patch_size
  18.         self.n_channels = n_channels
  20.     def forward(self, x): # B x C x H X W
  21.         x = x.unfold(
  22.             2, self.patch_size[0], self.patch_size[0]
  23.             ).unfold(
  24.                 3,self.patch_size[1],self.patch_size[1]
  25.                 )  # (B, C, P_row, P_col, P_height, P_width)
  26.         x = x.flatten(2)  #(B, C, P_row*P_col*P_height*P_width)
  27.         x = x.transpose(1, 2)  # (B,  P_row*P_col*P_height*P_width, C)
  28.         return x
  30. #实例化模型
  31. patch = Patch(img_size, patch_size, n_channels)
  33. #提取块
  34. with torch.no_grad():
  35.     patches = patch(image)
  37. #可视化
  38. patches = patches.squeeze(0)  # 删除批次维度 -> (P, d_model)
  39. patches = patches.view(-1, patch_size[0], patch_size[1]) # 重塑为 8x8
  41. npatches = img_size[0] // patch_size[0]
  42. #  绘制块
  43. fig, axs = plt.subplots(npatches, npatches, figsize=(6, 6))  # (32x32) -> 16 个块的 4x4 网格
  45. for i in range(npatches):
  46.     for j in range(npatches):
  47.         patch_idx = i * npatches + j  #块索引
  48.         axs[i, j].imshow(patches[patch_idx], cmap="gray", vmin=0, vmax=1)
  49.         axs[i, j].axis("off")
  51.  plt.show()

如代码所示，核心操作发生在 

  1. Patch

类的 

  1. forward

方法中。该类继承自 

  1. nn.Module

，其 

  1. forward

方法首先沿高度维度进行展开，然后再沿宽度维度进行展开。代码注释中展示了每一步操作后张量的维度，其中 B 代表批次大小，C 代表通道数（在本例中为 1），H 代表高度，W 代表宽度。展开操作之后，从存储图像数据的第二个维度开始展平张量，最后转置张量，以便颜色通道位于最后一个维度。

代码的剩余部分用于实例化 

  1. Patch

类，转换图像并将其可视化。需要注意的是，在可视化之前，需要先删除批次维度，然后将一维的图像数据转换回二维张量，才能正确显示图像块。

图像块嵌入的创建

上述方法在某种程度上将嵌入维度限制为原始图像尺寸的倍数。为了打破这个限制，可以在展开操作之后添加一个线性投影层，从而创建一个可学习的嵌入。

上图展示了在线性变换中使用单位矩阵（左）、在线性变换中使用随机权重（中）以及在线性变换中使用随机权重和偏差项（右）之后的图像块。

为了便于可视化，这些嵌入被转换回二维张量，从而展示了线性投影层如何对图像块进行操作。使用单位矩阵作为 

  1. nn.Linear

类的权重初始化，表明原始数据得以保留。使用随机权重，可以看到图像中具有零值的部分保持不变。最后，添加一个偏差项表明该变换确实平等地影响了每个图像块——所有空白图像块都显示出完全相同的偏差。

以下是新的 

  1. PatchEmbedding

类及其实例化代码。注意，这里引入了一个新的变量 

  1. d_model

，它代表期望的输出嵌入的维度。

  1. d_model

可以是任意数值。这里选择 

  1. d_model=64

是为了与上面图像的设置保持一致，但实际上不再有任何限制。

  1.  class PatchEmbedding(nn.Module):
  2.     def __init__(self, img_size, patch_size, n_channels, d_model):
  3.         super().__init__()
  4.         self.patch_size = patch_size
  5.         self.n_channels = n_channels
  6.         self.d_model = d_model
  8.         # 线性投影层，用于将每个块映射到 d_model
  9.         self.linear_proj = nn.Linear(patch_size[0] * patch_size[1] * n_channels, d_model,bias=False)
  10.         # 接下来的两行是不必要的，但有助于可视化线性
  11.         # 投影沿正确的维度运行
  12.         with torch.no_grad():
  13.           self.linear_proj.weight.copy_(torch.eye(self.linear_proj.weight.shape[0]))
  14.         
  15.     def forward(self, x): # B x C x H X W
  17.         x = x.unfold(
  18.             2, self.patch_size[0], self.patch_size[0]
  19.             ).unfold(
  20.                 3,self.patch_size[1],self.patch_size[1]
  21.                 )  # (B, C, P_row, P_col, P_height, P_width)
  22.         
  23.         B, C, P_row, P_col, P_height, P_width = x.shape
  24.         x = x.reshape(B,C,P_row*P_col,P_height*P_width)
  25.         x = self.linear_proj(x)  # (B*N, d_model)
  27.         x = x.flatten(2)  #(B, C, P_row*P_col*P_height*P_width)
  28.         x = x.transpose(1, 2)  # (B,  P_row*P_col*P_height*P_width, C)
  30.         x = x.view(B, -1, self.d_model)
  31.         
  32.         return x
  34. d_model = 64
  35. # 实例化模型
  36.  patch = PatchEmbedding(img_size, patch_size, n_channels, d_model)

只要维度是二次的，我们仍然可以可视化结果，下图展示了 

  1. d_model=4

和 

  1. d_model=2500

时的输出：

上图展示了嵌入到 4 维（左）和 2500 维（右）向量后的数字“2”的图像。

可以看到，非线性变换（一个全连接的神经网络，它接受从 8x8 (64) 到 

  1. d_model

的输入）可以包含相当多的可学习参数，从左侧的 64x4 (256) 到右侧的 64x2500 (160k)。可以使用以下代码自行测试：

  1.  def count_parameters(model):
  2.      return sum(p.numel() for p in model.parameters() if p.requires_grad)
  3.  
  5.  count_parameters(patch)

使用 2D 卷积创建图像块嵌入

  1. unfold

算子使用起来比较繁琐。实际上有一种更简单的方法可以将展开和线性变换结合起来，那就是使用 2D 卷积，并设置卷积核大小和步长长度与期望的图像块大小相对应。这样卷积操作将不再逐像素进行，而是逐图像块进行，从而产生与组合使用 

  1. unfold

和 

  1. nn.Linear

相同的结果：

上图展示了使用 2D 卷积将创建图像块和线性变换组合在一个步骤中的方法。顶行展示了嵌入到 4、64 和 2500 维的 16x16 图像块，底行展示了嵌入到 4、64 和 2500 维的 8x8 图像块。

以下是修改后的 

  1. PatchEmbedding

类：

  1.  class PatchEmbedding(nn.Module):
  2.     def __init__(self, img_size, patch_size, n_channels, d_model):
  3.         super().__init__()
  4.         self.patch_size = patch_size
  5.         self.n_channels = n_channels
  6.         self.d_model = d_model  #展平的块大小
  8.         # 用于提取块的 Conv2d
  9.         self.linear_project = nn.Conv2d(
  10.             in_channels=n_channels,
  11.             out_channels=self.d_model,  # 每个块都展平为 d_model
  12.             kernel_size=patch_size,
  13.             stride=patch_size,
  14.             bias=False
  15.         )
  17.     def forward(self, x):
  18.         x = self.linear_project(x)  # (B, d_model, P_row, P_col)
  19.         x = x.flatten(2)  # (B, d_model, P_row * P_col) -> (B, d_model, P)
  20.         x = x.transpose(1, 2)  # (B, P, d_model)
  21.          return x

可以将上述任何一种图像块嵌入方法提供给 Vision Transformer。使用 2D 卷积进行操作是最通用又是最紧凑的表示形式。需要注意的是，卷积操作为每个维度使用一个专用的卷积核，而到目前为止，我们一直在为每个图像块使用相同的卷积核。

可以通过初始化卷积核权重来演示这一点，并测试卷积操作是否执行任何有趣的操作，例如让每个卷积核仅提取每个图像块的单个像素。以下代码适用于图像块大小为 (8,8) 且生成的 

  1. d_model=64

的情况。将其添加到 

  1. PatchEmbedding

类的 

  1. __init__

方法的末尾：

  1.          """Initialize Conv2d to extract patches without transformation.""" // 初始化 Conv2d 以提取没有转换的块。
  2.         with torch.no_grad():
  3.             identity_kernel = torch.zeros(
  4.                 self.d_model, self.n_channels, *self.patch_size
  5.             )  # Shape: (64, 1, 8, 8)
  7.             for i in range(self.d_model):  
  8.                 row = i // self.patch_size[1]  # 块中的行索引
  9.                 col = i % self.patch_size[1]   #块中的列索引
  10.                 identity_kernel[i, 0, row, col] = 1  # 在正确的像素位置放置 1
  12.              self.linear_project.weight.copy_(identity_kernel)

如代码所示，

  1. identity_kernel

张量维护 

  1. d_model

个条目，每个维度一个，并且每个图像块只有一个像素设置为 1，从而仅提取该像素。一种更简单的方法是将 

  1. d_model

x 

  1. d_model

的单位矩阵简单地转换为 

  1. patch_size

的 

  1. d_model

矩阵：

  1.          identity_matrix = torch.eye(self.d_model)
  2.          identity_kernel = identity_matrix.view(d_model, 1, *patch_size)  # Shape: (64, 1, 8, 8)
  3.  
  5.          with torch.no_grad():
  6.               self.linear_project.weight.copy_(identity_kernel)

两种方法都具有相同的结果，但第一种方法更清楚地说明了实际发生的情况：每个卷积核都是一个零矩阵，只有一个条目为 1。

无论使用线性变换还是小卷积核的集合，两者都具有相同数量的参数。可以通过检查两个图像块嵌入的数据结构来看到这一点：

  1.  PatchEmbedding(
  2.    (linear_proj): Linear(in_features=64, out_features=64, bias=False)
  3.  )

和

  1.  PatchEmbedding(
  2.    (linear_project): Conv2d(1, 64, kernel_size=(8, 8), stride=(8, 8), bias=False)
  3.  )

其中一个只是一个 64x64 矩阵（4096 个参数）。另一个由 64 个 8x8 矩阵组成，也由 4096 个参数组成。

总结

这篇文章通过理论讲解和实际代码相结合的方式,全面介绍了Vision Transformer中图像块嵌入的实现细节,对理解和实现Vision Transformer具有重要的参考价值。Vision Transformer中图像块嵌入,使Transformer能够统一处理图像、文本等多模态数据。

本文通过理论讲解和实际代码相结合的方式，全面介绍了 Vision Transformer 中图像块嵌入的实现细节。文中的代码示例和可视化结果有助于更好地理解这一关键过程。

作者：Nikolaus Correll

标签： 深度学习 Vision Transformer 图像块嵌入
登录后发布评论

“Vision Transformer中的图像块嵌入详解：线性投影和二维卷积的数学原理与代码实现”的评论:

还没有评论
关于作者
...
Deephub
更多文章请关注公众号：Deephub-IMBA
相关阅读

标签噪声下的模型评估：如何准确评估AI模型的真实性能，提高模型性能测量的可信度

VideoMind：Chain-of-LoRA突破时间盲区让AI真正看懂长视频

9个主流GAN损失函数的数学原理和Pytorch代码实现：从经典模型到现代变体

DAPO: 面向开源大语言模型的解耦裁剪与动态采样策略优化系统

多模态AI核心技术：CLIP与SigLIP技术原理与应用进展

SWEET-RL：基于训练时信息的多轮LLM代理强化学习框架

时间序列异常检测：MSET-SPRT组合方法的原理和Python代码实现