
从上世纪五十年代开始,似乎所有的机器学习算法——无论是 logistic 回归,还是支持向量机——都是随着神经网络的诞生而发展起来的。
从这个意义上讲,神经网络更像是一个框架和概念,而不仅仅是一个算法。并且在构建神经网络时有着巨大的自由度:隐藏层数量、节点数量、激活函数、优化器、损失函数、网络类型(卷积、递归等)和特殊层(batch norm、 dropout等)。
从这个角度来看,神经网络是一个概念,而不是一个严格的算法,这是一个非常有趣的推论:任何机器学习算法,无论是决策树还是k-最近邻,都可以用神经网络来表示。我们既可以直觉上通过一些例子来理解,也可以在数学上进行证明。
首先,让我们定义什么是神经网络:它是一个由输入层、隐藏层和输出层组成的体系结构,每个层的节点之间都有连接。信息通过线性变换(权重和偏差)以及非线性变换(激活函数)从输入层转换到输出层。有一些方法可以更新模型的可训练参数,从而使模型具有更好的可训练性。
Logistic回归被简单地定义为一个回归算法,每个输入都有权重,并且增加了一个额外的偏差,所有这些参数都传递给sigmoid函数以实现回归。可以用一个不含隐藏层、以sigmoid函数作为激活函数的神经网络实现同样的效果。
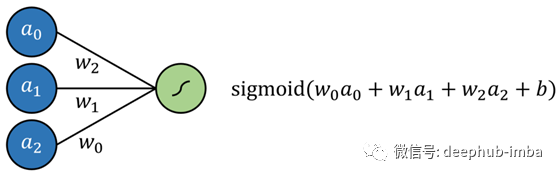
而线性回归同样可以用一个不含隐藏层的神经网络实现,其中激活函数选用线性函数。
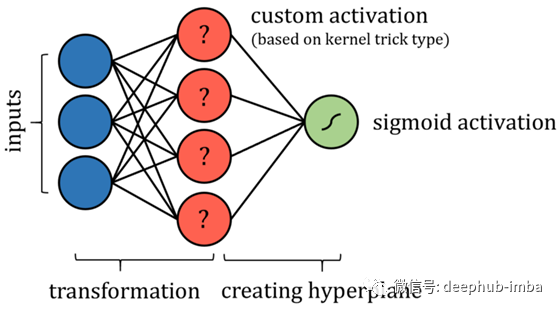
支持向量机(SVM)算法试图通过一种所谓的“核技巧”将数据投影到一个新的空间中,从而优化数据的线性可分性。在数据被转换后,该算法绘制出沿着类边界最好地分离数据的超平面。超平面被简单地定义为现有维度的线性组合,就像二维的直线和三维的平面。从这个意义上讲,我们可以把支持向量机算法看作是将数据投影到一个新的空间,然后进行多元回归。神经网络的输出可以通过某种有界输出函数来获得与SVM相同的概率结果。当然,可能需要一些额外的限制,例如限制节点之间的连接,并使某些参数固定不变,或者需要添加更多的层。
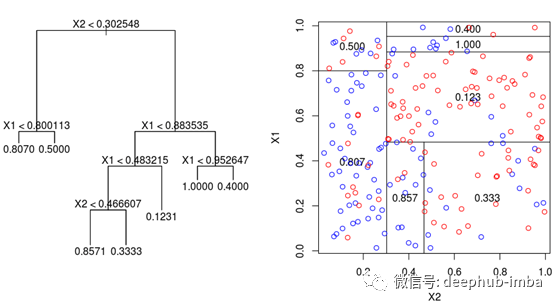
基于树的算法,比如决策树算法,要稍微复杂一些。关于如何构造这种神经网络的关键在于分析它如何划分其特征空间。当训练点穿过一系列分割的节点时,特征空间被分割成几个超立方体;在二维场景下,数据空间被垂直线和水平线划分成若干个长方形。因此,沿着这些线分割特征空间的类似形式可以通过更严格的激活函数来模拟实现,比如阶跃函数(本质上是一条分隔线)。
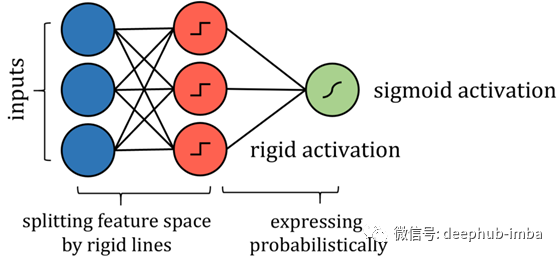
虽然神经网络替代算法与实际算法有许多技术上的差异,但表达了相同的思想,并且能够以与实际算法相同的策略和性能来处理问题。其关键在于万能逼近定理——神经网络疯狂成功背后的数学解释——它本质上说,一个足够大的神经网络可以以任意精度对任何函数建模。假设有一个函数f(x),对于每个数据点(x,y),f(x)总是能够返回一个等于或非常接近真实值的数据。
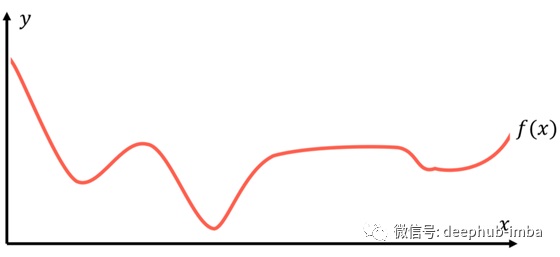
建模的目的是找到这个有代表性的或基本的真值函数f(x),f(x)描述如何实现输入数据与目标数据的映射。

传统的方法有时候作用显著,有时候作用不尽如人意。因为这些方法只有固定数量的参数。相对而言,神经网络在寻找f(x)的方法上有所不同。
根据微分的思想,任何函数都可以用许多类似阶梯的部分来合理地近似,阶梯越多,逼近就越精确。
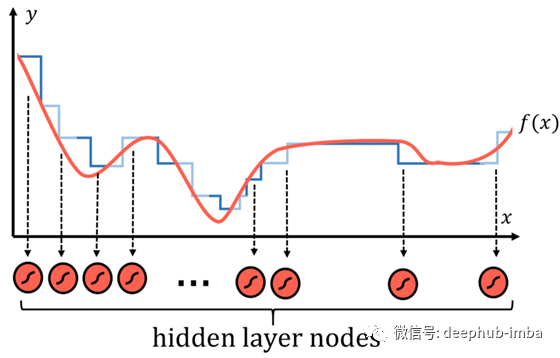
在神经网络中,每一个阶梯都可以是隐层节点的sigmoid激活函数,它本质上是一个概率阶跃函数。每个节点都被“分配”到f(x)函数的一部分。然后,通过权值和偏差系统,网络可以确定一个节点的存在,如果一个特定的输入应该激活神经元,则将sigmoid函数的输入放至正无穷大(输出为1),反之则朝负无穷大方向变化。这种委托节点寻找数据函数特定部分的模式不仅可以应用到数值数据中,而且也可以应用到图像中。
通用逼近定理现在已经被扩展到适用于其他激活函数,如ReLU,但结论仍然正确:神经网络是为了完美而创建的,它可以逼近任意函数。神经网络不再依赖复杂的数学方程和关系系统,而是将自己的一部分委托给数据函数的一部分,并在其指定区域内强力记忆归纳。当这些节点聚合成一个庞大的神经网络时,结果是一个看似智能的模型,而实际上它们是被巧妙设计的近似器。
假设神经网络至少在理论上可以构造出一个基本上和你想要的一样精确的函数(节点越多,近似值越精确,当然不考虑过拟合的技术细节),一个结构正确的神经网络可以对任何其他算法的预测函数p(x)进行替代建模。而对于其他任何机器学习算法来说,这是不可能实现的。神经网络对其他算法的替代建模所使用的方法不是优化现有模型中的一些参数,如多项式曲线或节点系统。它寻求的不是充分利用任何已有独立系统,而是直接对数据进行近似逼近的方式。
作者:Andre Ye
deephub翻译组:Oliver Lee
推荐阅读
DeepHub
微信号 : deephub-imba
每日大数据和人工智能的重磅干货
大厂职位内推信息
长按识别二维码关注 ->
喜欢就请三连暴击!********** **********