【机器学习】朴素贝叶斯算法

    朴素贝叶斯（Naive Bayes）是经典的机器学习算法之一，也是为数不多的基于概率论的分类算法。由于朴素贝叶斯计算联合概率，所以朴素贝叶斯模型属于生成式模型。经典应用案例包括：文本分类、垃圾邮件过滤等。

1.贝叶斯公式

       贝叶斯公式又被称为贝叶斯规则，是概率统计中的应用所观察到的**现象**对**有关概率分布**的主观判断（先验概率）进行修正的标准方法。如果你看到一个人总是做一些好事，则那个人多半会是一个好人。这就是说，当你不能准确知悉一个事物的本质时，你可以依靠**与事物特定本质相关的事件出现的多少去判断其本质属性的概率**。用数学语言表达就是：**支持某项属性的事件发生得愈多，则该属性成立的可能性就愈大**。贝叶斯公式中涉及到**先验概率**、**后验概率**、**条件概率**等，具体解释如下。

    **先验概率**：即基于统计的概率，是基于以往历史经验和分析得到的结果，不需要依赖当前发生的条件。

   ** 后验概率**：则是从条件概率而来，由因推果，是基于当下发生了事件之后计算的概率，依赖于当前发生的条件。

   ** 条件概率**：记事件A发生的概率为P(A)，事件B发生的概率为P(B)，则在B事件发生的前提下，A事件发生的概率即为条件概率，记为P(A|B)，读作“在B条件下A的概率”。

    **联合概率**：表示两个事件共同发生的概率。A与B的联合概率表示为P(AB),或者P(A,B),或者P（A∩B）。

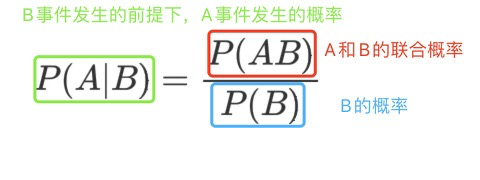
** 贝叶斯公式：贝叶斯公式便是基于条件概率P(B|A)求的联合概率**，再求得P(A|B)。

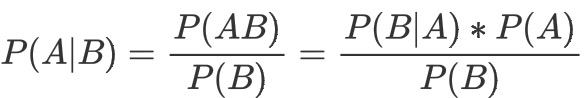
     将A看成“类别”，B看成“属性”，那么贝叶斯公式看成：

2.朴素贝叶斯算法的原理

    朴素贝叶斯分类器是一类简单的概率分类器，在**强（朴素）独立性假设**的条件下运用贝叶斯公式来计算每个类别的后验概率，假设**每个特征之间没有联系。**

** 通俗的解释：已知结果(先验概率)，结果与在此结果为条件下出现的现象（条件概率）相乘的到结果和现象同时发生的联合概率**。除以现象单独发生的概率，就得出在某现象发生的条件下，发生结果的概率（后验概率）

3.案例

    **问题**：给出下列训练数据*(X,Y)*共计17条数据，*X*是属性集合（色泽、根蒂、敲声、纹理、脐部、触感、密度、含糖率），*Y*是类别标记（是否是好瓜）。这时来了一个新的样本“测1”，我们想要预测它的类别y（是否是好瓜）。

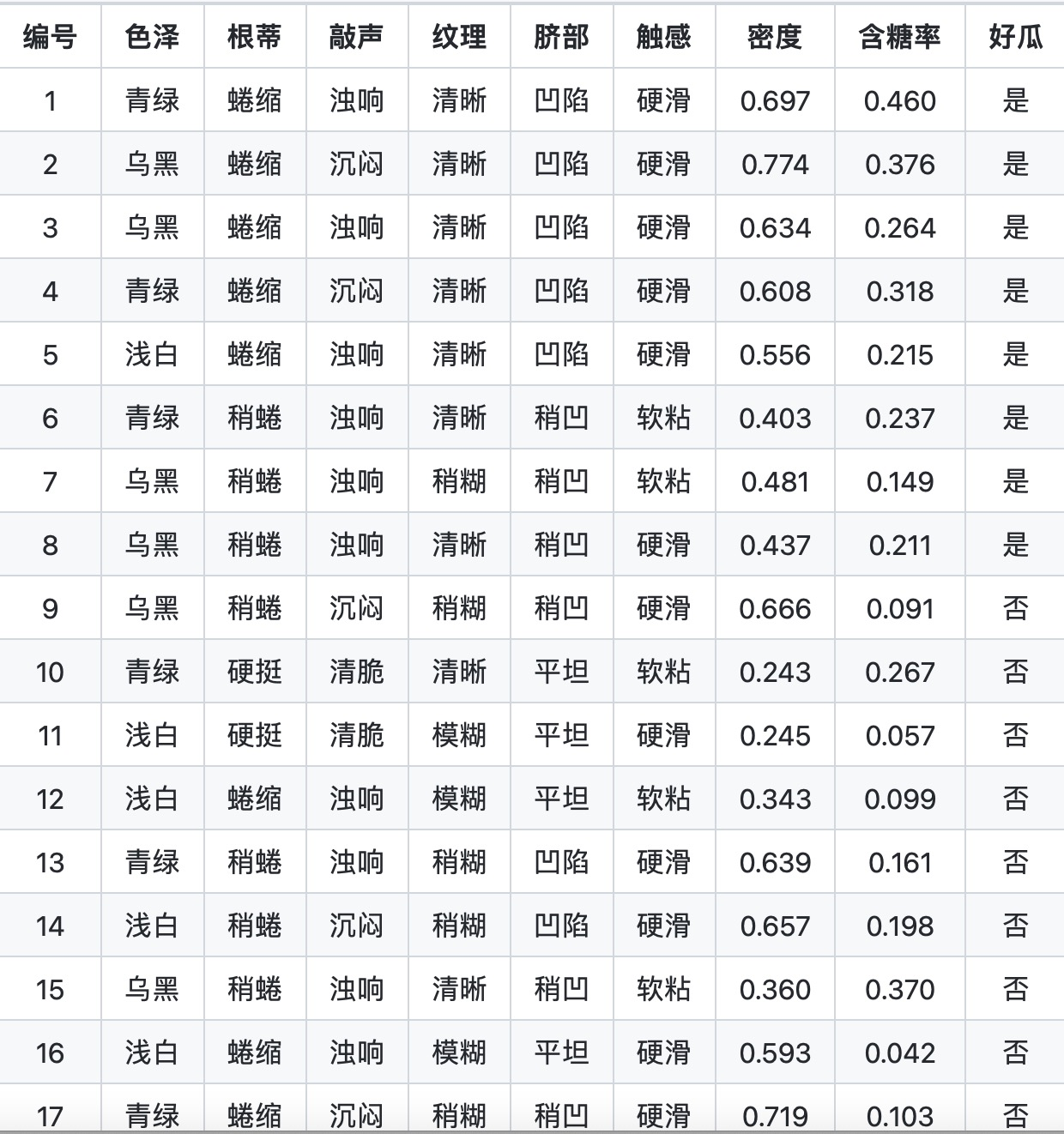
    首先，计算类别的**先验概率**。在17个样例中，有8个是好瓜，9个不是好瓜，我们可以根据给出的样例，得出是否是好瓜的先验概率。

     然后，为“测1”中给定的属性估计**条件概率**。针对**测试样例给定的属性值**统计在好瓜=是和好瓜=否中的数量，为计算条件概率提供数据。

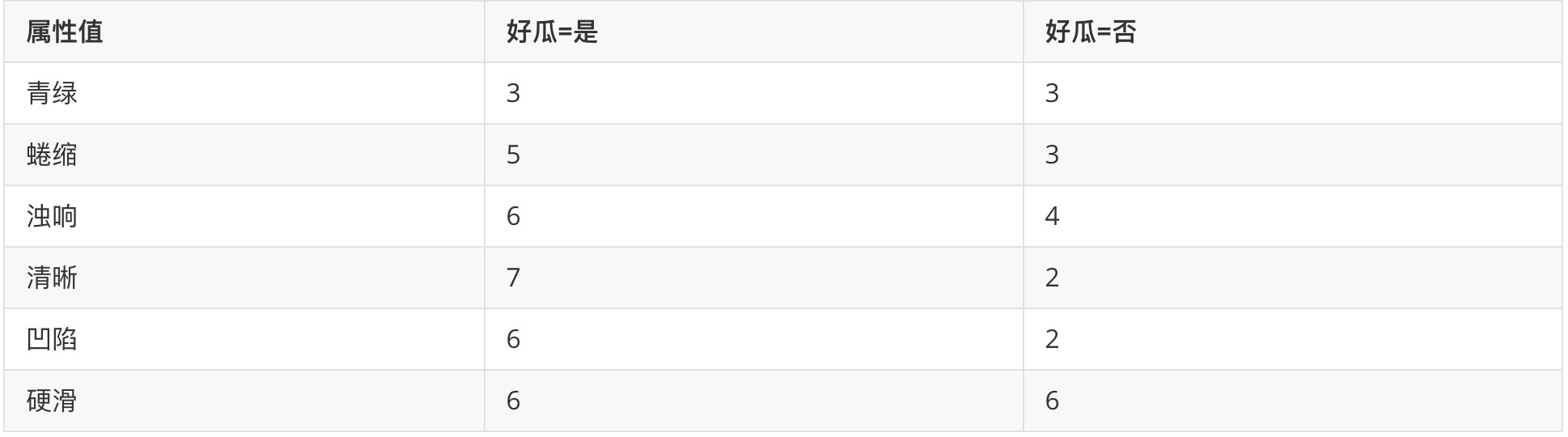
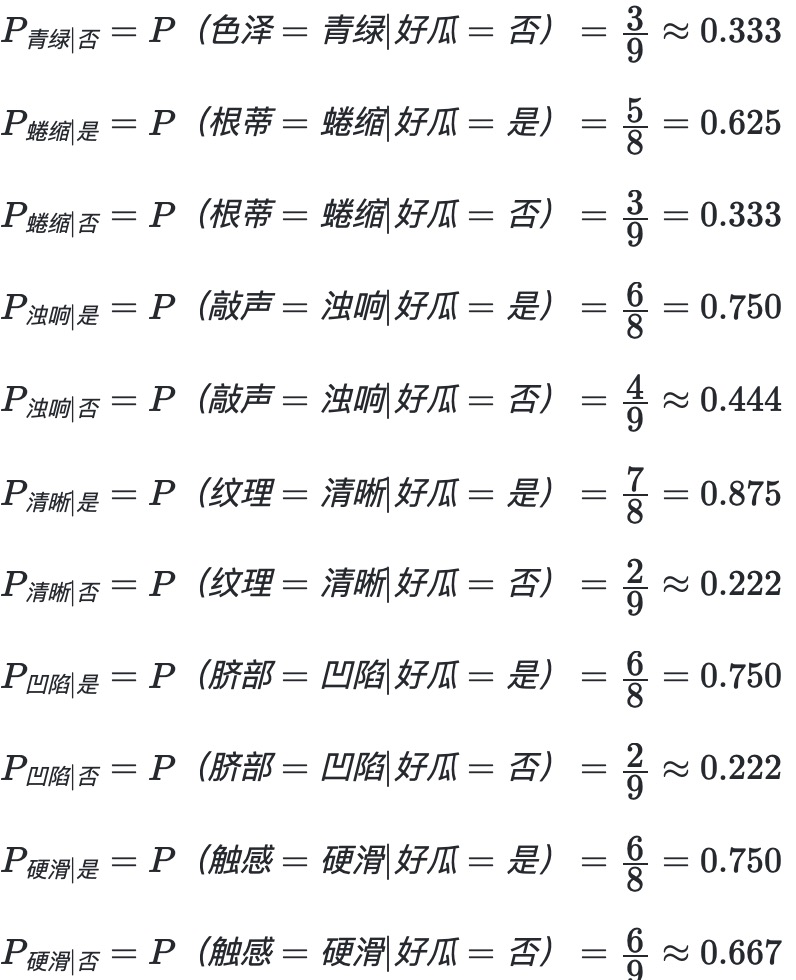
     对于数值属性，一般假设**同一类别中**的**属性值**服从正态分布，首先计算**当前类别**与**所在属性下的属性值**分布的均值和方差，然后计算**当前属性值**在这个分布中的概率密度。计算公式如下所示。

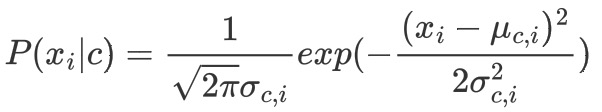
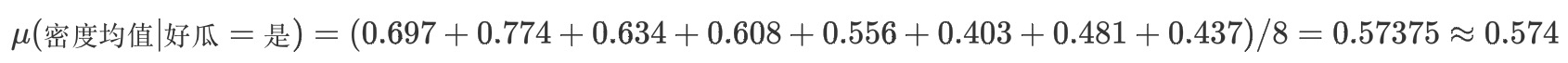
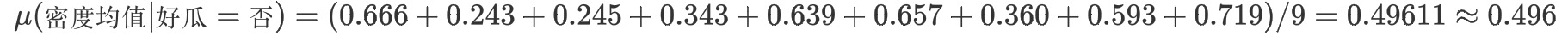
     按照均值和方差公式计算出'好瓜=是'的密度均值、密度方差，'好瓜=否'的密度均值、密度方差，'好瓜=是'的含糖量均值、含糖量方差，'好瓜=否'的含糖量均值、含糖量方差。并且将其带入公式的到条件概率。

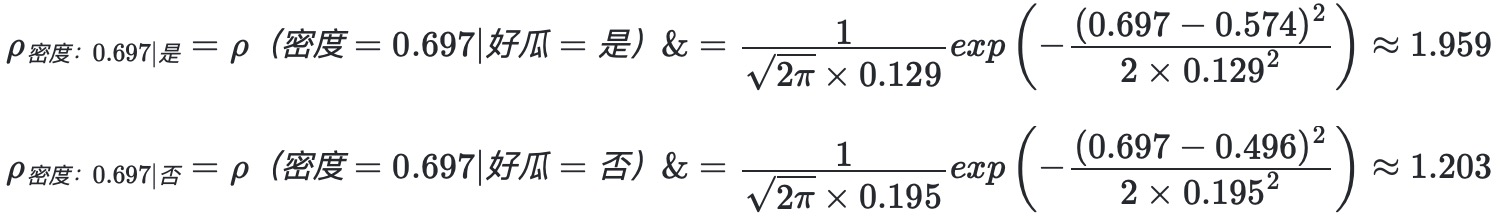
    将计算结果代入公式。比较结果，0.063>>0.0000680,因此，朴素贝叶斯分类器将测试样本“测1”判别为“好瓜”。![](https://img-blog.csdnimg.cn/b3404487c1dd4e208eece467c058d10a.png)

Reference:

    1.https://blog.csdn.net/kevinjin2011/article/details/125099177