手搓人工智能-距离分类器

距离分类器

距离分类器的形式：

    距离分类器的目的是将需要识别的样本 **![x](https://latex.csdn.net/eq?x) **分类到与其最相似的类别中。如果能够度量 **![x](https://latex.csdn.net/eq?x) **与每个类别的相似程度

$s(x,\omega_{i}) ,i=1,2...$

    那么接下来能够采用以下方式进行分类：

$j=\underset{1\leqslant i \leqslant n }{\arg max s (x,\omega _{i})},x \in \omega_{j}$

    这是一种常用的数学化表达方式，其含义为：如果 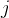![j](https://latex.csdn.net/eq?j) 在所有 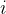![i](https://latex.csdn.net/eq?i) 可能的取值中，使得相似程度![s(x,\omega_{i})](https://latex.csdn.net/eq?s%28x%2C%5Comega_%7Bi%7D%29) 取得最大值，则判别 ![x](https://latex.csdn.net/eq?x) 属于类别 ![\omega _{j}](https://latex.csdn.net/eq?%5Comega%20_%7Bj%7D)

距离分类器的一般算法：

输入需要识别的样本 $x$
计算 $x$ 与所有类别的相似程度 $s(x,\omega_{i}) ,i=1,2...$
输出相似度最大的类别 $\omega _{j}$

模板匹配

模板匹配的含义

    假设你在寻找照片中某个特定的物体，比如一个苹果。你可以把苹果的图像（这就是“模板”）放在一个图像中，与其他区域进行比较。模板匹配就是通过比较模板和图像中的每个部分，来找到与模板最相似的区域。

    在每个类别只有一个代表样本的情况下，最自然的方法就是用待识别样本 ![x](https://latex.csdn.net/eq?x) 与类别代表样本之间的相似程度作为样本与类别相似程度的度量：

$s(x,\omega_{i}) = s(x,\mu _{i})$

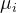    ![x](https://latex.csdn.net/eq?x) 和 ![\mu_{i}](https://latex.csdn.net/eq?%5Cmu_%7Bi%7D) 均为特征矢量，可以看作 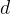![d](https://latex.csdn.net/eq?d) 维特征空间中的两个点，所以可以很自然的用两者之间的“距离”来度量相似程度。由于使用“距离”度量样本之间及样本类别之间的相似程度是一种最常用的方法，所以本文介绍的分类器被称为“距离分类器”，相应分类方法被称为“模板匹配”

模板匹配的步骤

    将特征空间划分为 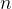![n](https://latex.csdn.net/eq?n) 个区域，每个区域中的点距离该区域中的代表模板最近。

    两个区域的交界一般称为“判别界面”，在二维特征空间中是一条垂直平分两个类别代表样本连线的直线，在三维空间中是垂直平分的平面，而在高维空间中被称为“超平面”。

最近邻分类

     每个类别已知所有的训练样本可以表示成一个集合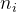![D_{i} = \{ x_1^{(i)},...,x_n^{(i)}\}, i=1,2,..,c](https://latex.csdn.net/eq?D_%7Bi%7D%20%3D%20%5C%7B%20x_1%5E%7B%28i%29%7D%2C...%2Cx_n%5E%7B%28i%29%7D%5C%7D%2C%20i%3D1%2C2%2C..%2Cc), ![n_i](https://latex.csdn.net/eq?n_i) 为第 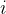![i](https://latex.csdn.net/eq?i) 个类别中的训练样本数。样本 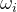![x](https://latex.csdn.net/eq?x) 与类别 ![\omega_i](https://latex.csdn.net/eq?%5Comega_i) 之间的相似程度可以用 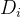![x](https://latex.csdn.net/eq?x) 与 ![D_i](https://latex.csdn.net/eq?D_i) 中最近样本的距离来衡量：

$s(x,\omega_i)=\underset{y\in D_i}{min\ d(x,y)}$

最近邻分类算法（NN）：

输入需要识别的样本 $x$ ，训练样本集 $D=\{ x_1, x_2,...,x_n \}$
寻找 $D$ 中与 $x$ 最近的样本： $y=\underset{x_i \in D}{arg\ min\ d(x,x_i)}$
输出 $y$ 所属的类别

最近邻分类器的加速

    提高近邻分类器识别速度的根本方法是减少待识别样本与训练样本之间距离的计算次数

转化为单模板匹配

    减少最近邻算法计算量最直接的方法是用每个类别的训练样本学习出一个模板 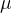![\mu](https://latex.csdn.net/eq?%5Cmu) 来代表这个类别，待识别样本 ![x](https://latex.csdn.net/eq?x) 只需要与每个类别的代表模板 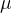![\mu](https://latex.csdn.net/eq?%5Cmu) 计算距离，以这个距离来度量 ![x](https://latex.csdn.net/eq?x) 与类别之间的相似程度。

    根据这个思路，每个类别的代表模板可以通过求解一个优化问题得到：

$\mu_i = \underset{\mu \in R^d}{arg \ min} \sum_ {k =1}^{n_i}d(x_k^{(i)},\mu)$

    因为代表模板不一定是 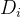![D_i](https://latex.csdn.net/eq?D_i) 中的某个样本，因此优化问题是在整个 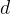![d](https://latex.csdn.net/eq?d) 维欧式空间中寻找一个最优矢量。距离度量 ![d(x_k^{(i)},\mu)](https://latex.csdn.net/eq?d%28x_k%5E%7B%28i%29%7D%2C%5Cmu%29) 可以选择最常用的欧式距离，为了计算方便，也可以对距离平方求和：

$J_i(\mu)=\sum_{k=1}^{n_i}\left | \left | x_k^{(i)}-\mu \right | \right |^2=\sum_{k=1}^{n_i} (x_k^{(i)}-\mu)^T(x_k^{(i)}-\mu)$

$\mu_i=\underset{\mu \in R^d}{arg \ min \ J_i(\mu)}$

    优化问题可以通过令 ![J_i(\mu)](https://latex.csdn.net/eq?J_i%28%5Cmu%29) 的梯度等于零矢量求解极值点：

$\bigtriangledown J_i(\mu)=\frac{\partial J_i(\mu)}{\partial \mu}=\sum_{k=1}^{n_i}2(x_k^{(i)}-\mu)(-1)=2n_i\mu-2\sum_{k=1}^{n_i}x_k^{(i)}=0$

    （这里有点问题，先这么放着）解得极值点为：

$\mu_i=\frac{1}{n_i} \sum_{k=1}^{n_i} x_k^{(i)}$

转化为多模板匹配

    当每个类别样本分布的区域都接近球形，不同类别样本之间距离较远时，单模板匹配可以取得很好的分类效果。但是样本不满足以上情况时，单模板匹配会导致许多样本被错误分类。

    对于这种情况，一个有效的解决办法是将每个类别的训练样本根据距离的远近划分为若干个子集，子集中的样本分别计算平均值，每个均值都作为一个模板，用多个模板来代表每个类别的训练样本：

$j=\underset{1\leqslant i \leqslant c }{arg\ min} [\underset{1\leqslant k \leqslant m_i}{min}d(x,\mu_i^k)],x \in \omega_j$

剪辑近邻算法

    降低近邻分类器计算复杂度的另一种方法是在训练阶段对样本集合进行“剪辑”，删除掉某些“无用”的样本，减少训练样本的数量

输入 $D=\{ x_1,x_2,...,x_n \}$
构造 $D$ 的 $Voronoi$ 网格 // 见第二幅图
寻找与 $x_i$ 相邻的所有网格，如果所有相邻的网格与 $x_i$ 都属于同一类别，则标记 $x_i$
删除 $D$ 中被标记的样本，重新构造 $Voronoi$ 网格

K - 近邻算法（KNN）：

K - 近邻分类

    当训练样本中存在噪点，个别样本可能会被标记错误，或者会导致样本某些特征在特征空间中发生偏移，当待识别样本以噪声样本为最近邻时，对其类别的判断就会发生错误。

    K - 近邻算法是对最激烈算法的一个自然推广，样本类别的判断不再只依赖于其最近的一个样本，而是由距离最近的K个样本决定。

$j=\underset{1 \leqslant i \leqslant c} {arg \ max \ k_i},x \in \omega_j$

输入需要识别的样本 $x$ ，训练样本集 $D=\{ x_1,x_2,...,x_n \}$ ，参数 $K$
计算 $x$ 与 $D$ 中每个样本的距离
寻找与 $x$ 距离最近的前 $K$ 个样本，统计其中属于各个类别的样本数 $k_i,i=1,2,...,c$
输出 $j=\underset{1 \leqslant i \leqslant c}{arg \ max \ k_i}$

K - D 树构建算法

    K - D 树是一种提高 K - 近邻算法计算效率的手段：如果样本是无序的，那么只能逐个比较或排序，如果样本是有序的，就可以采用折半查找，将计算复杂度从 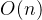![O(n)](https://latex.csdn.net/eq?O%28n%29) 降为 ![O(log_2 n)](https://latex.csdn.net/eq?O%28log_2%20n%29)。

输入非空训练样本集 $D=\{ x_1,x_2,...,x_n \}$
计算 $D$ 中每一维特征的方差，选择方差最大的特征 $s$
排序 $D$ 中所有样本的第 $s$ 维特征，选择位于中间的样本作为根节点，并记录 $s$
将 $D$ 所有第 $s$ 维特征小于根节点的样本放入左子集 $D_L$ ，递归调用建树过程，将得到的 K - D数作为根节点的左子树
将 $D$ 所有第 $s$ 维特征大于根节点的样本放入右子集 $D_R$ ，递归调用建树过程，将得到的 K - D数作为根节点的右子树
输出 K - D树

C++ 示例代码

KNN：

class KNNClassifier {
public:
    KNNClassifier(int k) : k(k) {}
    void fit(const vector<DataPoint>& data) {
        trainingData = data;
    }
    int predict(const vector<double>& testPoint) {
        // 计算距离并排序
        vector<pair<double, int>> distances;
        for (const auto& dataPoint : trainingData) {
            double distance = euclideanDistance(dataPoint.features, testPoint);
            distances.push_back(make_pair(distance, dataPoint.label));
        }
        // 按距离排序
        sort(distances.begin(), distances.end());
        // 找到k个最近邻
        map<int, int> labelCount;
        for (int i = 0; i < k; ++i) {
            labelCount[distances[i].second]++;
        }
        // 找到出现次数最多的标签
        int predictedLabel = -1;
        int maxCount = 0;
        for (const auto& pair : labelCount) {
            if (pair.second > maxCount) {
                maxCount = pair.second;
                predictedLabel = pair.first;
            }
        }
        return predictedLabel;
    }
private:
    vector<DataPoint> trainingData; // 存储训练数据
    int k; // 最近邻数量
};

距离（后面会发更详细的）：

欧式距离：

double Distance::EuclideanDistance(std::vector<double> sample) {
    /*int x_size = sample.size();
    int y_size = sample.size();*/
    double Distance = 0;
    for (auto i = sample.begin(); i != sample.end(); i++) {
        double Distance = Distance + (*i * *i);
    }
    return sqrt(Distance);
}
double Distance::EuclideanDistance(std::vector<double> sample1, std::vector<double> sample2) {
    double Distance = 0;
    for (int i = 0; i < sample1.size(); i++) {
        double Distance = Distance + (sample1[i] - sample2[i]) * (sample1[i] - sample2[i]);
    }
    return sqrt(Distance);
}

曼哈顿距离：

double Distance::ManhattanDistance(std::vector<double> sample) {
    double Distance = 0;
    for (auto i = sample.begin(); i != sample.end(); i++) {
        double Distance = Distance + *i;
    }
    return Distance;
}
double Distance::ManhattanDistance(std::vector<double> sample1, std::vector<double> sample2) {
    double Distance = 0;
    for (int i = 0; i < sample1.size(); i++) {
        Distance = Distance + abs(sample1[i] - sample2[i]);
    }
    return Distance;
}

文献参考：

【1】刘家锋-模式识别

图片来源

【1】自制

【2】最近邻分类器 - 搜索 (bing.com)

【3】最近邻分类器 - 搜索图片 (bing.com)

标签：人工智能 c++ 线性代数

本文转载自: https://blog.csdn.net/weixin_73858308/article/details/142886639
版权归原作者 Karaoit 所有，如有侵权，请联系我们删除。