2022年秋季《数字图像处理》课程复习整理
文章目录
课程大纲

一、视觉与图像

1. 图像格式
PBM(bitmap) PGM(graymap)PPM(pixelmap)
TIFF(无损图像格式)、bmp、jepg、gif、png等
2. 图像获取
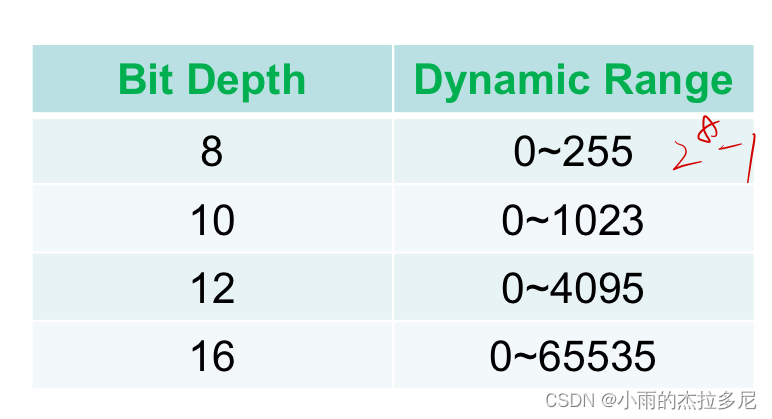
像素位深度:
如果8位三通道彩色图像,则变换范围就是
2
8
∗
2
8
∗
2
8
−
1
2^8*2^8*2^8-1
28∗28∗28−1
3. 采样与量化
简单成像模型:
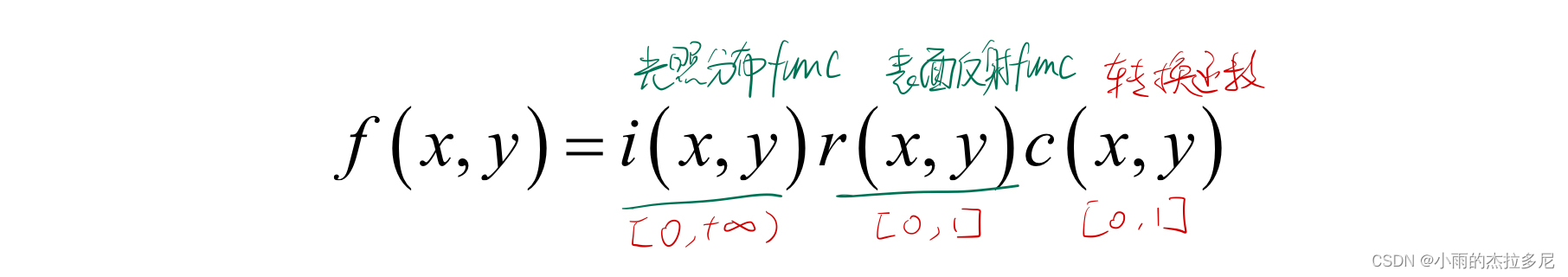
采样:空间坐标离散化
量化:采样点的灰度值离散化
空间采样由物理像素决定,灰度采样由模拟-数字决定。
4. 像素间的基本关系
二维平面:4邻域、8邻域
三维空间:27邻域(对应8邻域)
5. 像素集基本运算
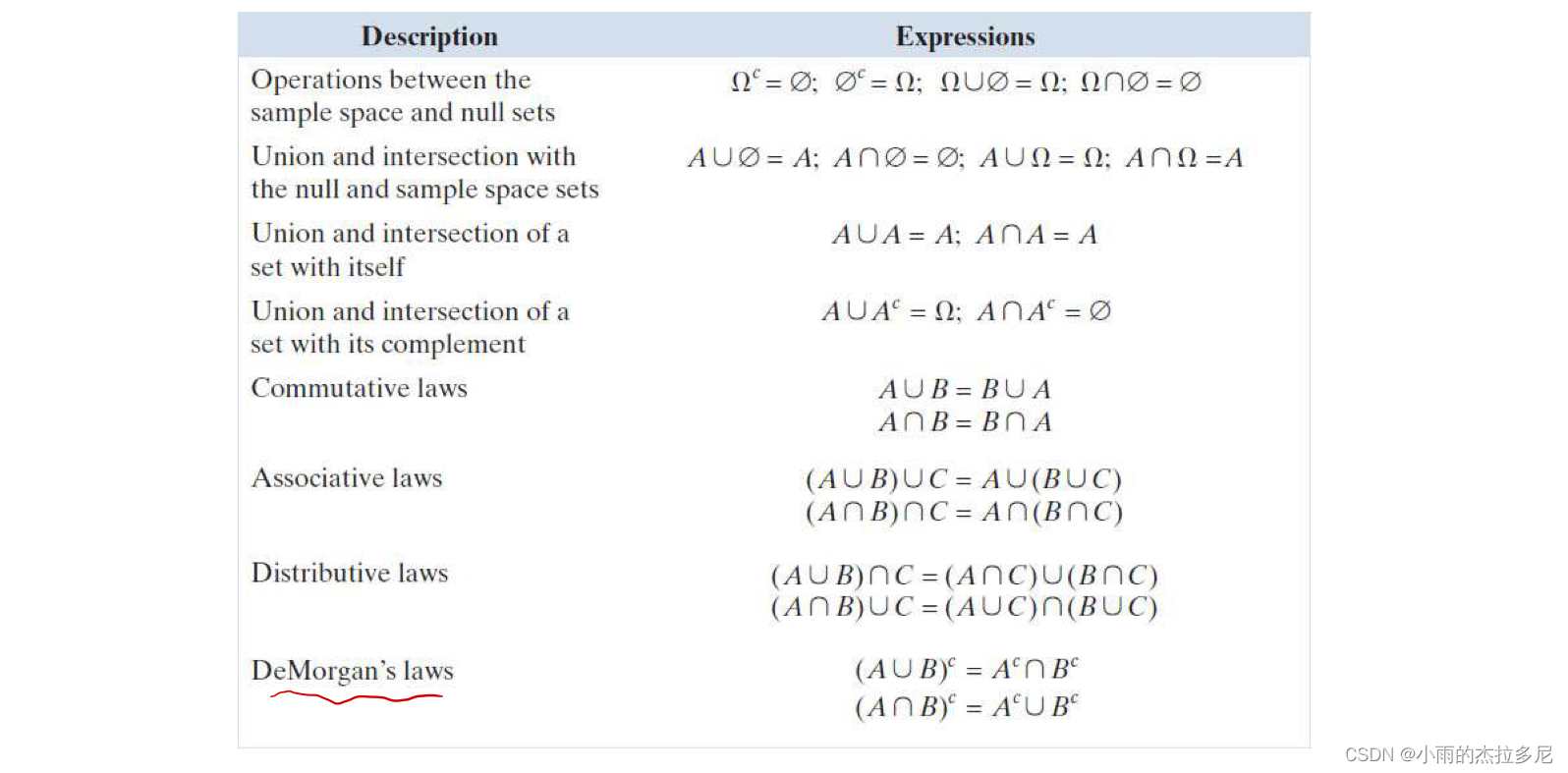
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-wq4RckN4-1674829553743)(/Users/jiaminggu/Downloads/img/IMG_07E809E725D5-1.jpeg)]](https://img-blog.csdnimg.cn/3dbef40552834438a2a96d6bc8968a28.jpeg)
线性算子:满足齐次性、可加性(回忆矩阵课中)
6. 彩色图像
CMYK比RGB更适合打印
Hue:色调,Saturation:饱和度,Intensity:强度,Lightness:亮度,Value:亮度
二、图像变换与滤波
1. 点扩散函数
psf函数(point spread function)
OTF函数(optical transfer function)就是psf的傅立叶变换,在频域的函数。
一个复杂图像的像I(x,y)可以看作是真实对象O(x,y)和psf函数的卷积。
在频域的乘积就是空间域的卷积
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-IDx2n4We-1674829553743)(/Users/jiaminggu/Downloads/img/IMG_E6067E9475C2-1.jpeg)]](https://img-blog.csdnimg.cn/186735d2121349d58f14732a076e14a9.jpeg)
其中h(x, y)是degradation退化过程, yeta(x,y)是噪声。一个图像g就是这么构成的。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-N6xYLIic-1674829553743)(/Users/jiaminggu/Downloads/img/IMG_DA31133FAFDC-1.jpeg)]](https://img-blog.csdnimg.cn/952110f1cecd4a2e9598832698fc753f.jpeg)
2. 空间滤波
卷积要翻转滤波核,并且相关不具有交换律和结合律
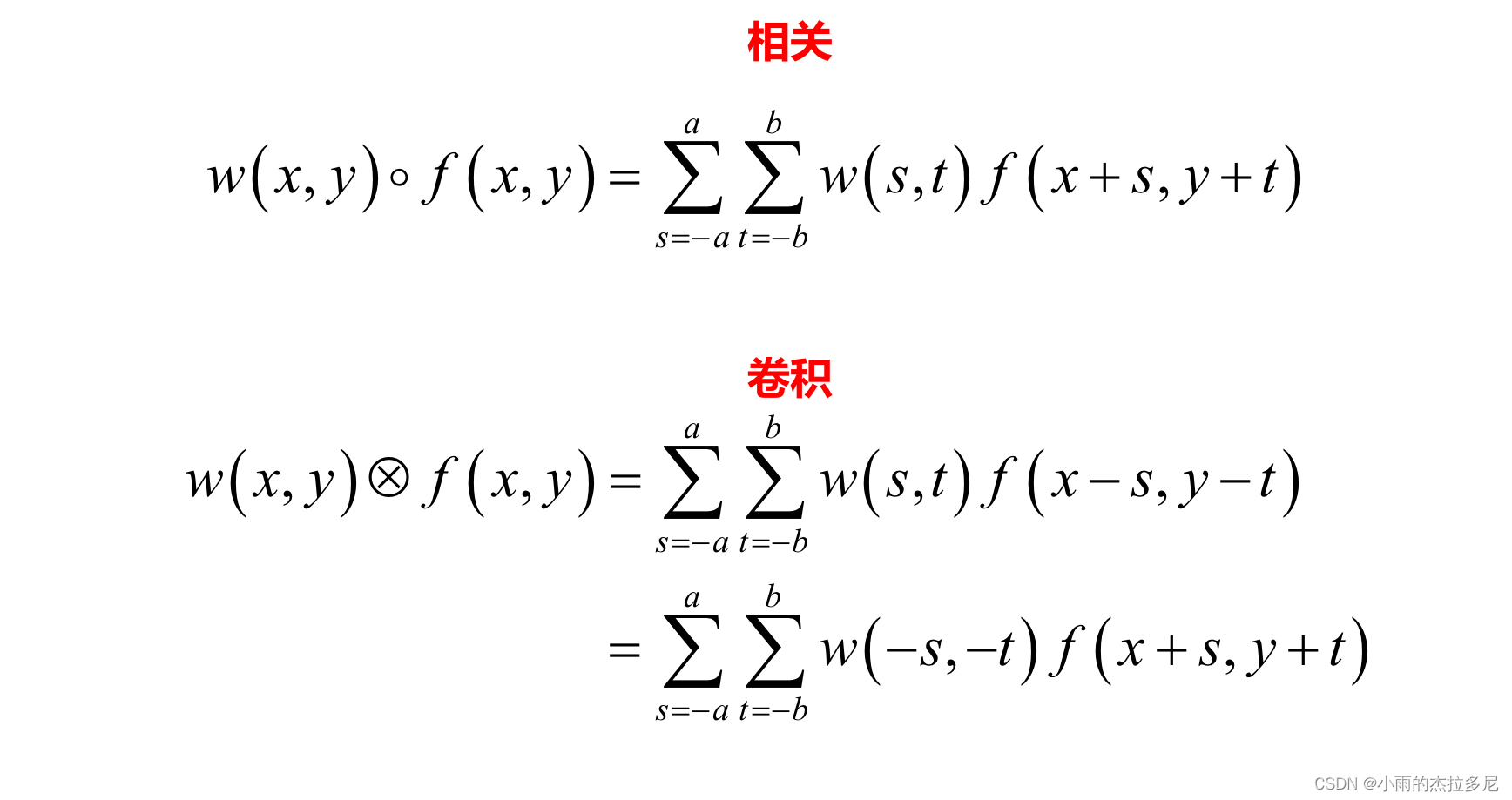
![]](https://img-blog.csdnimg.cn/a7f12a2ad12840dc92dd687d692fb7a2.jpeg)
图像导数的计算:
前向差分、后项差分、中心差分
f
′
(
x
)
=
f
(
x
+
h
)
−
f
(
x
−
h
)
2
h
+
O
(
h
2
)
f'(x) = \frac{f(x+h)-f(x-h)}{2h}+O(h^2)
f′(x)=2hf(x+h)−f(x−h)+O(h2)
图像求导会放大噪声:
设定前一项为图像,后一项为噪声
那么分量AS>AN,但频率WS<WN
A
S
s
i
n
(
W
s
t
)
+
A
N
s
i
n
(
W
N
t
)
A_Ssin(W_st)+A_Nsin(W_Nt)
ASsin(Wst)+ANsin(WNt)
这样每次求导,前一项都会求出来一个WS,后一项都会求出来一个WN
长远来看,噪声的比例会被方大,因为WS<WN
2.1 高斯滤波器
对于均值滤波器,在频域内是非单调的,这种特性是我们不希望看到的。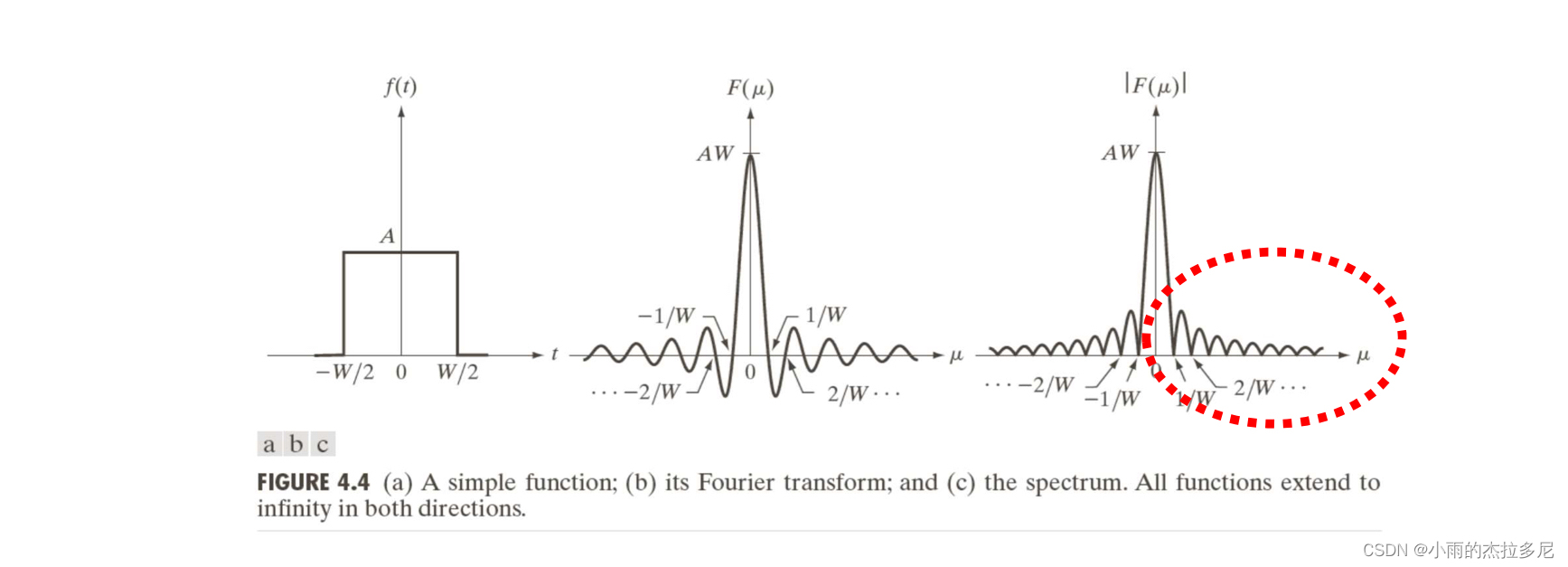
因此,考虑高斯滤波器,拥有低通和可分式两个特性。如果方差越大,则会损失越多的高频信息。

高斯滤波器的窗口大小 = ceiling(3 * sigma) * 2 + 1
原因(3sigma原则)在3sigma范围内就已经包含足够的信息了。
两边两个3sigma再加中间的元素。
2.2 高通滤波器
- 梯度锐化(比如梯度超过一定值用梯度替代,其他保持原像素)
- Laplacian增强算子(就是加大原先laplacian的中心系数)
3. 一维傅立叶变换 & 采样定理
傅立叶级数:其中e的j theta次方是欧拉公式
其中n代表要展开为n项,T是f(t)的周期
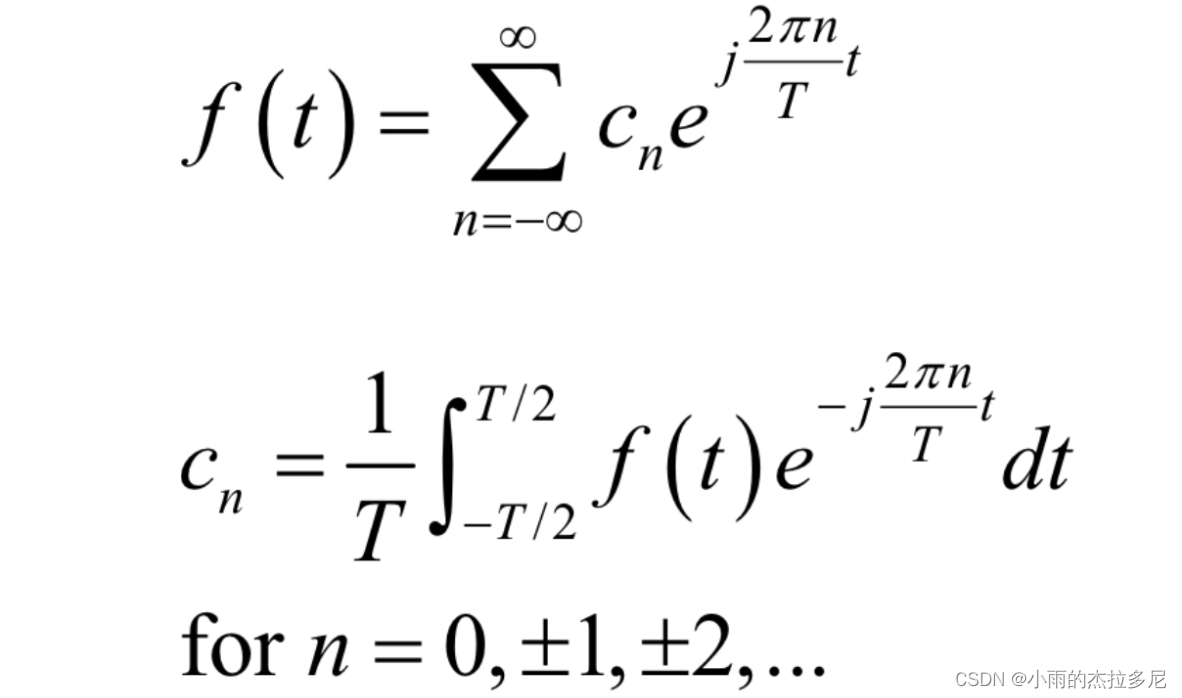
傅立叶变换:
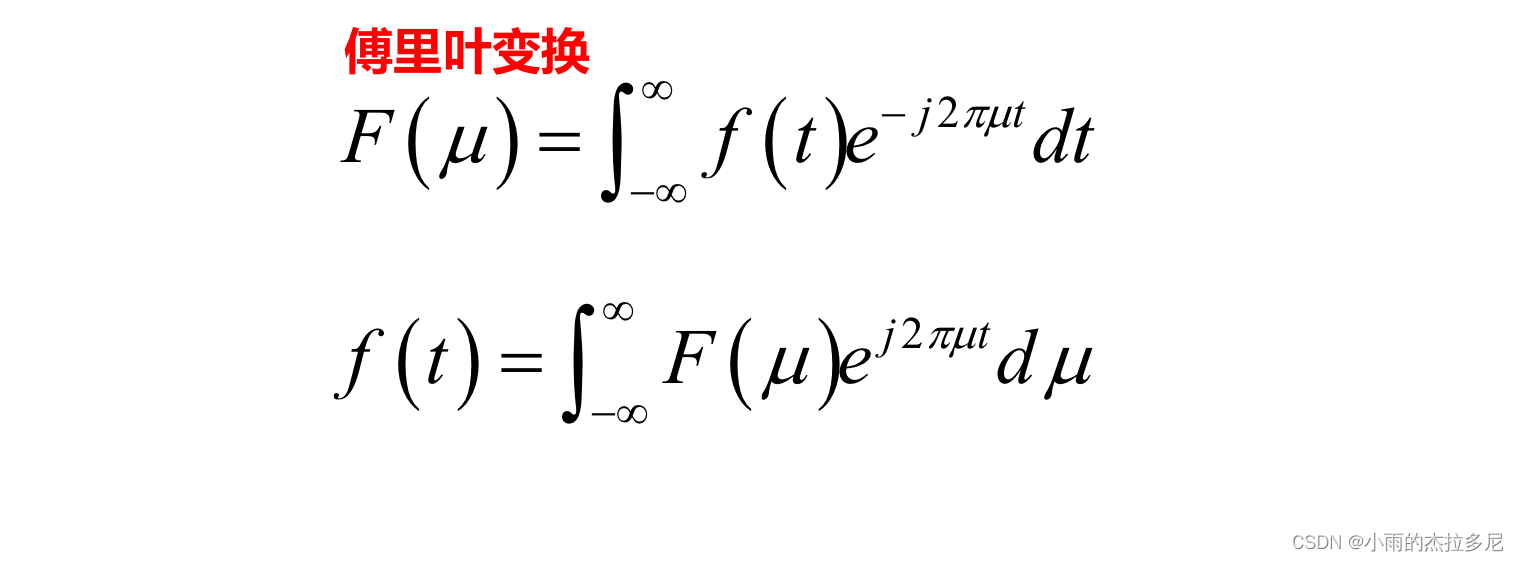
采样
采样的过程被看作是原函数与脉冲函数的乘积。
经过推导采样后的傅立叶变换是原函数傅立叶变换的无限、周期副本序列,间隔为deltaT。
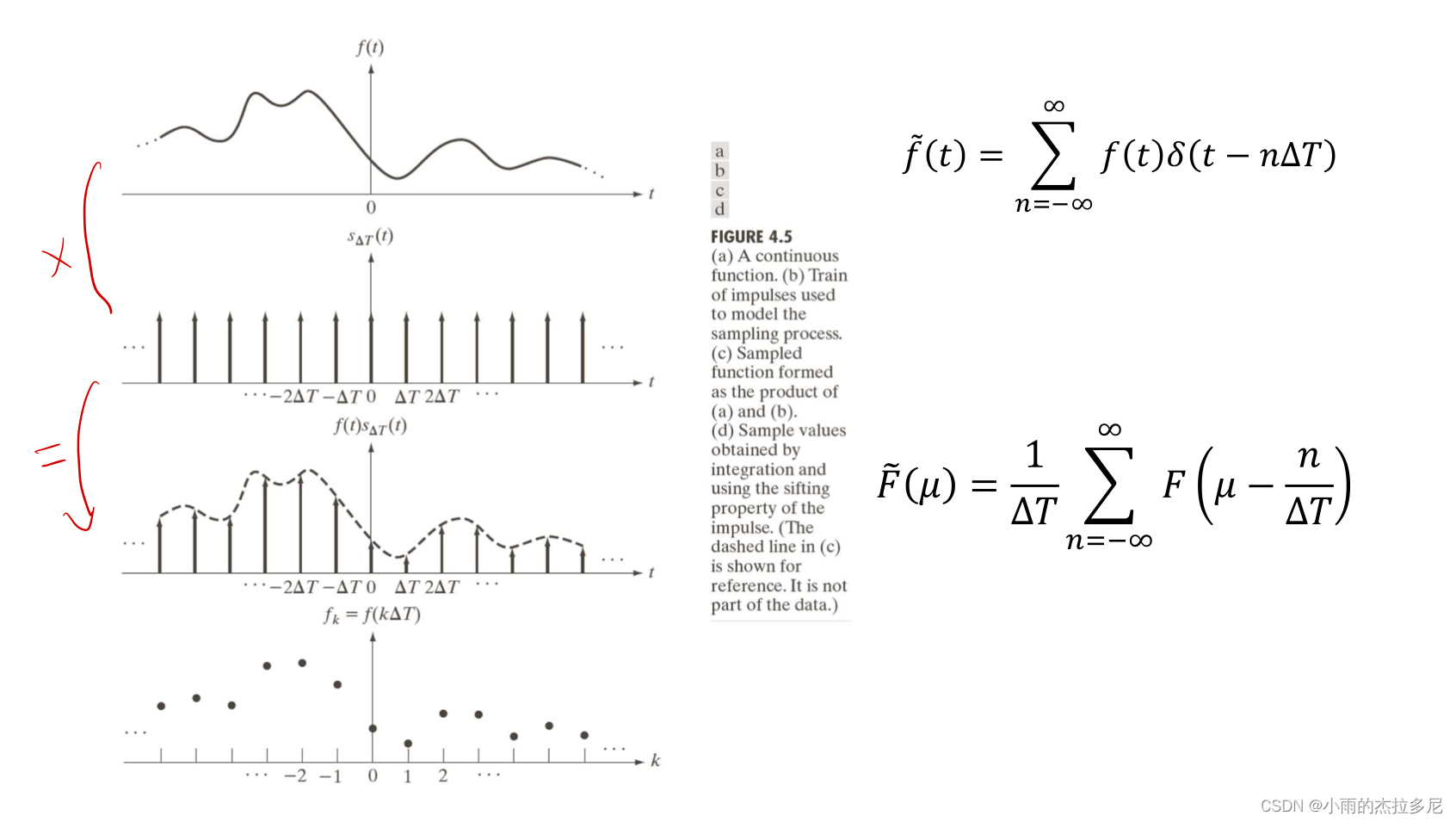
采样定理:
而1/deltaT是采样频率,采样频率要高于最大频率的两倍(即三角形的底边),才能防止产生混叠现象。才能成功恢复原始信号。这样的频率叫做
奈奎斯特率
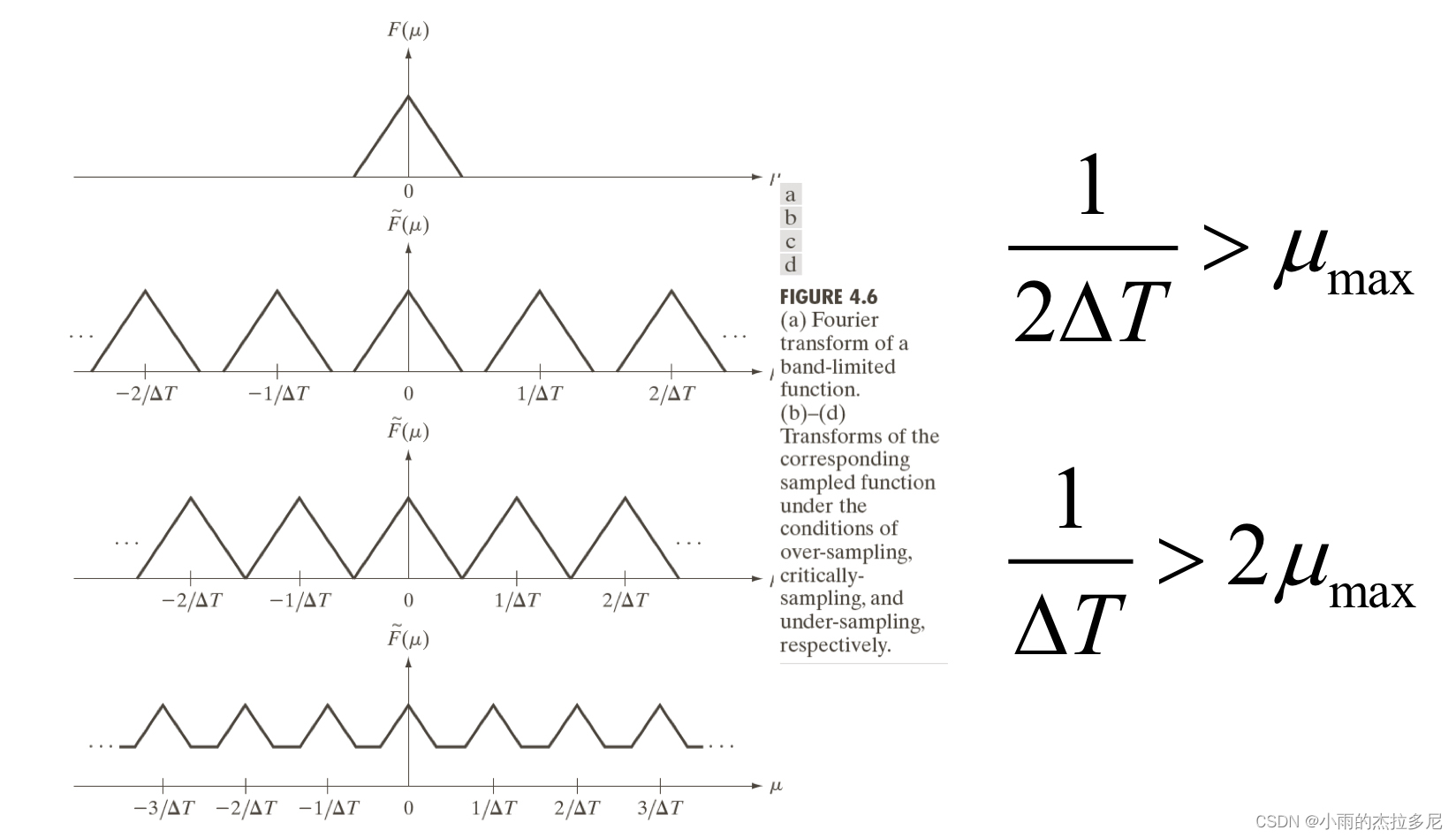
利用奈奎斯特率采样率恢复原始信号:
直接用H(u)乘采样后信号就可以得到一个周期的原始信号。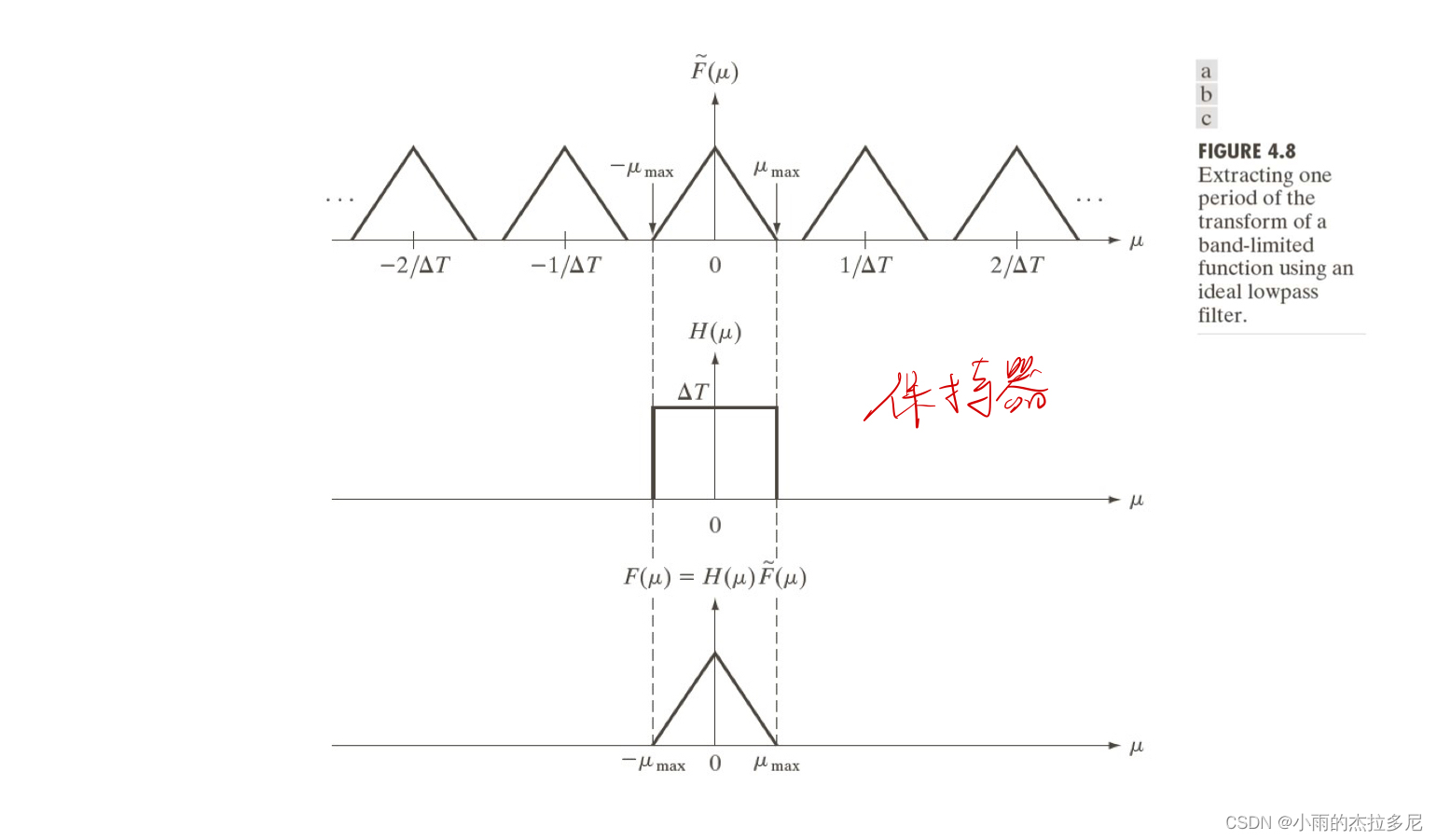
有限持续时间函数不可能是带限的(回忆
测不准原理
)
带限的是说在频域上无高频。
4. 二维傅立叶变换 & 采样定理

二维傅立叶变换具有可分性:(要会推导)
可以先对行做傅立叶变换,再对列做

逆向傅立叶变换步骤:
- 取共轭
- 做二维离散傅立叶变换
- 除MN,取共轭
要让周期移动到M/2的位置,让其中心出现在高频区域
f
(
x
)
e
j
2
π
(
μ
0
x
/
M
)
=
F
(
μ
−
μ
0
)
f(x)e^{j2\pi(\mu_0x/M)} = F(\mu - \mu_0)
f(x)ej2π(μ0x/M)=F(μ−μ0)
取mu_0是M/2,指数项就是(-1)^x
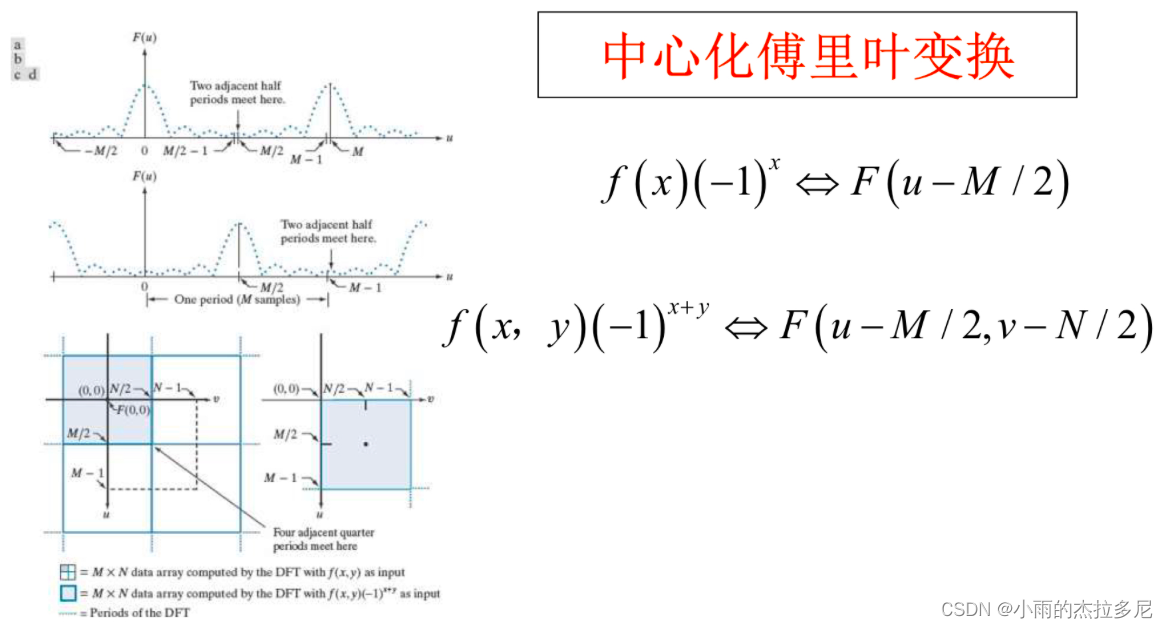
二维F的采样定理就是要在两个方向都大于奈奎斯特率,否则也会出现混叠现象。
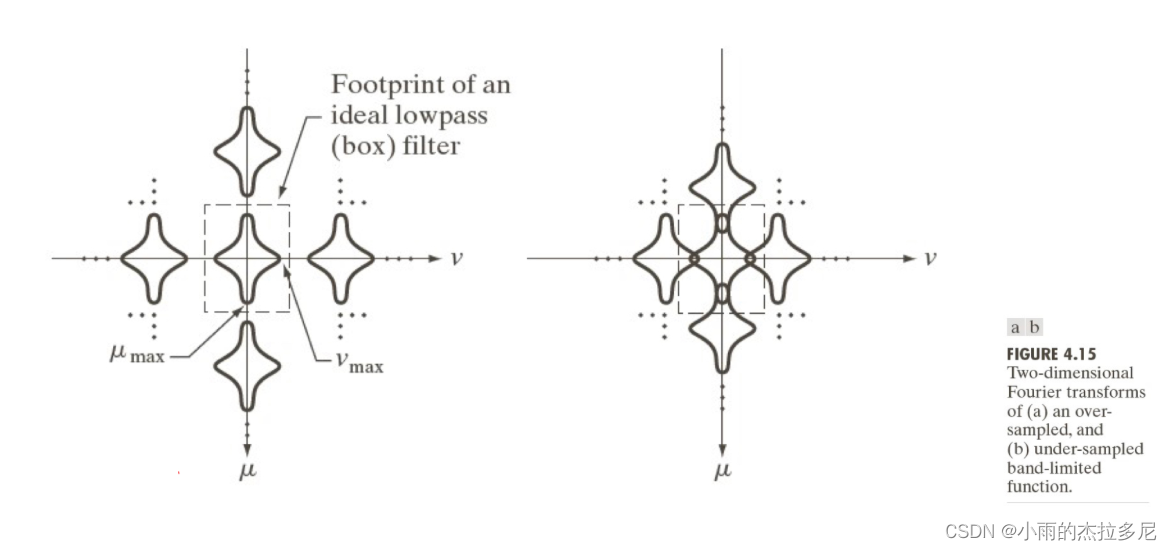
二维傅立叶变换的特性:
对称性、平移不变性、二维卷积定理等。。
FFT: 只需要知道计算复杂度即可,MlogM
5. 图像频率域滤波
步骤:
- 给定图像 f 进行傅立叶变换F
- 构建频率域滤波器H,乘F。得到结果G
- G逆变换回空间域
5.1 低通
理想低通滤波器,在空间域直接截断,在频域会产生振铃现象
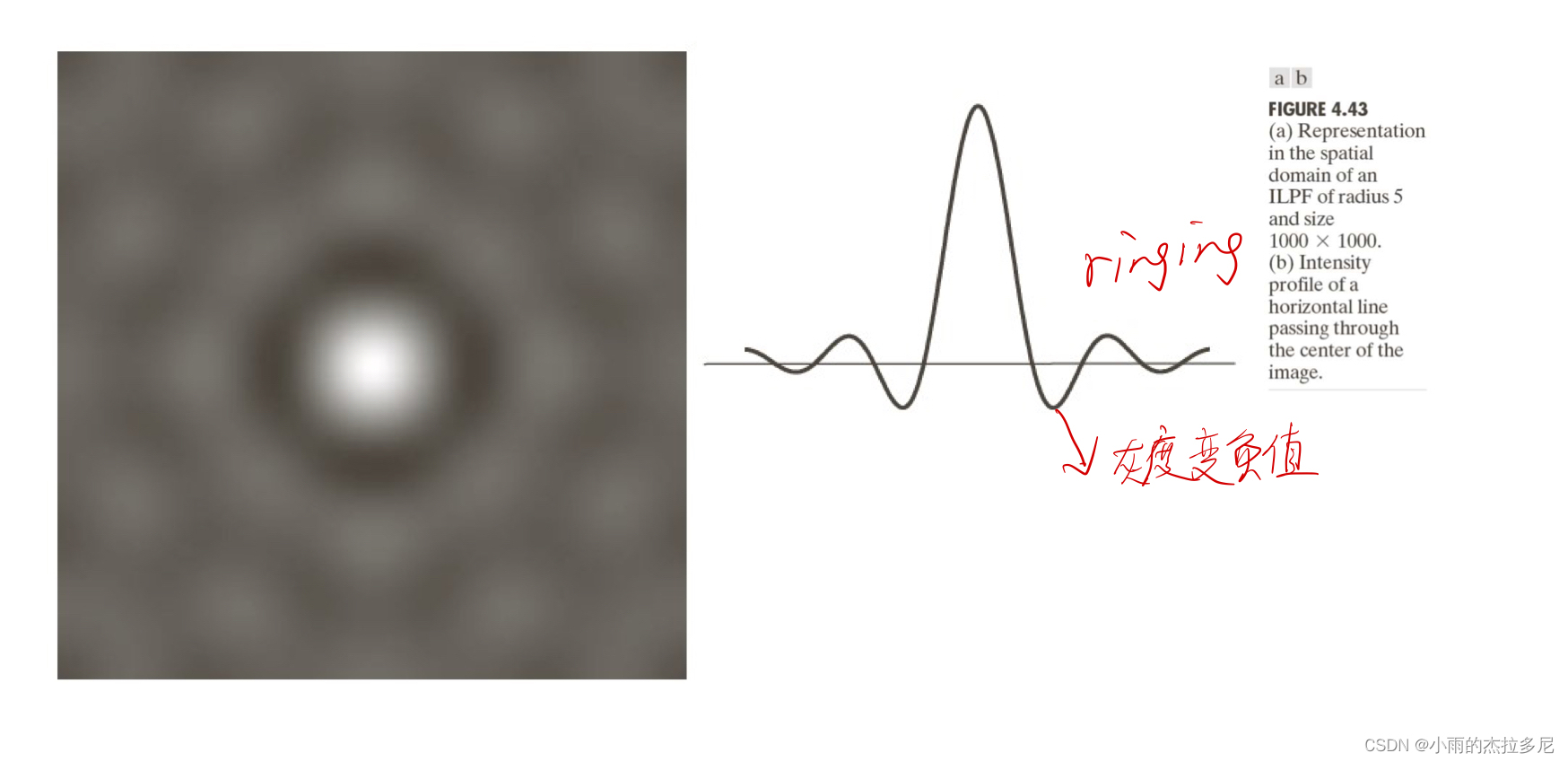
高斯低通滤波器虽然解决了ringing,但坡度过于平滑,模糊效果强烈。
巴特沃斯滤波器:
当n较大时,逼近于理想低通;当n较小时,逼近于高斯低通
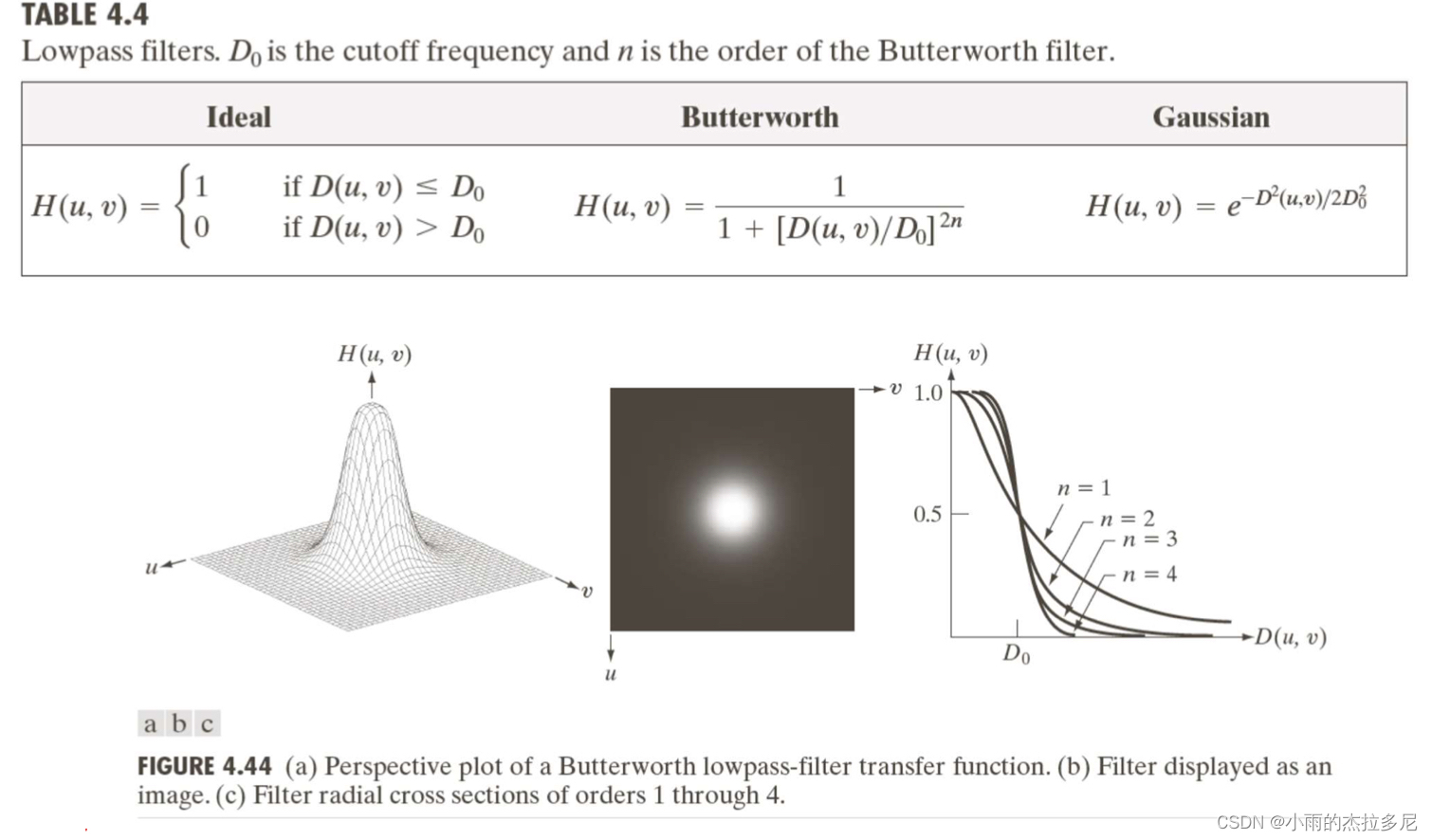
相对的,在空域上BLPF就也会有ringing,低阶不明显。
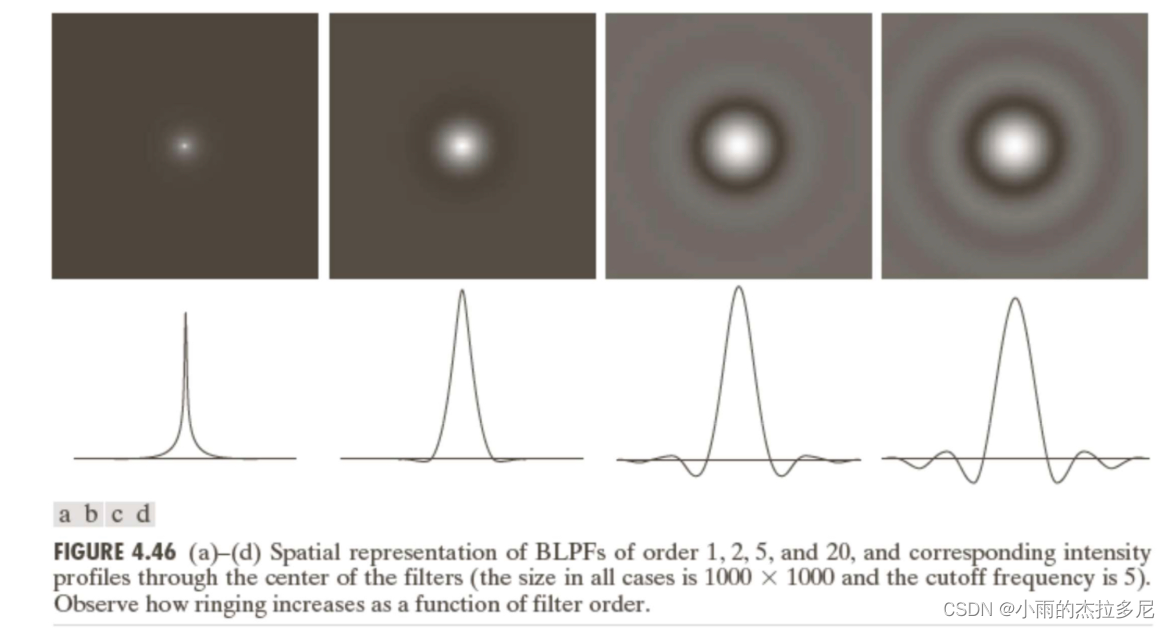
5.2 其他滤波器
选择性滤波器:带阻、带通(都有理想、高斯和巴特沃斯情况)


6. 线性系统补充
线性算子:满足可加性和齐次性的operator
特性1: fixed parameter(g(x+x_0) = H[f(x+x_0)])
特性2: causal
特性3: stable (有界)

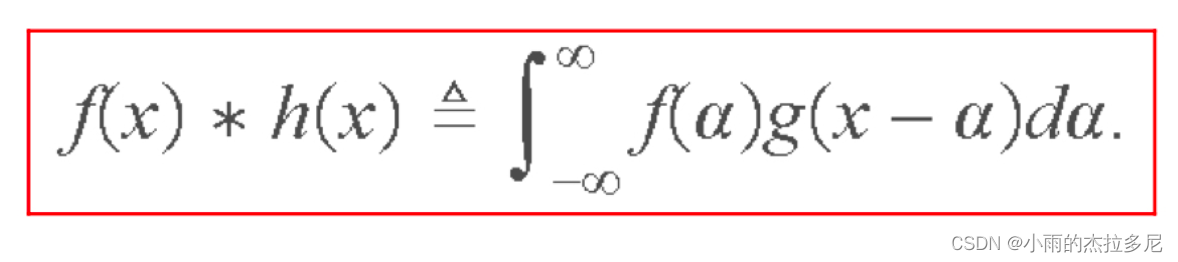
利用卷积公式和傅立叶变换,就可以推导空域卷积等于频域乘积了。
7. 图像滤波算子
Laplacian算子:就是求导数用的(1,-2,1)的纵横(斜角)的叠加

Roberts 只有2*2,检测斜方向梯度
Sobel、Prewitt、Scharr都是可以用来求边缘的
8. 正交变换
一维、二维傅立叶变换是一种正交变换
8.1 一维傅立叶变换

A矩阵的每一行都是一个变换核:

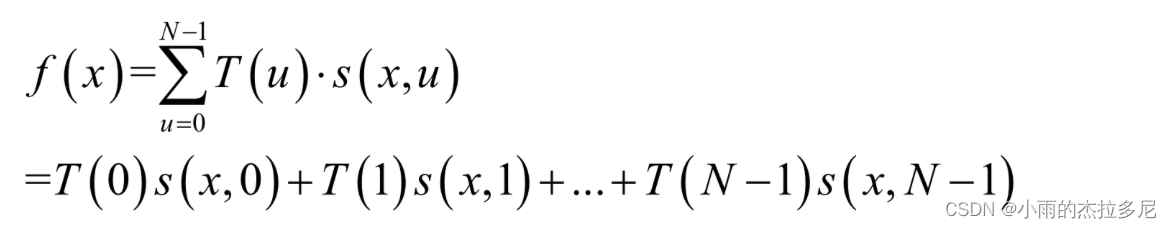
这里说明,A的第一列是r0,因为A是正交矩阵,第一行是s0。
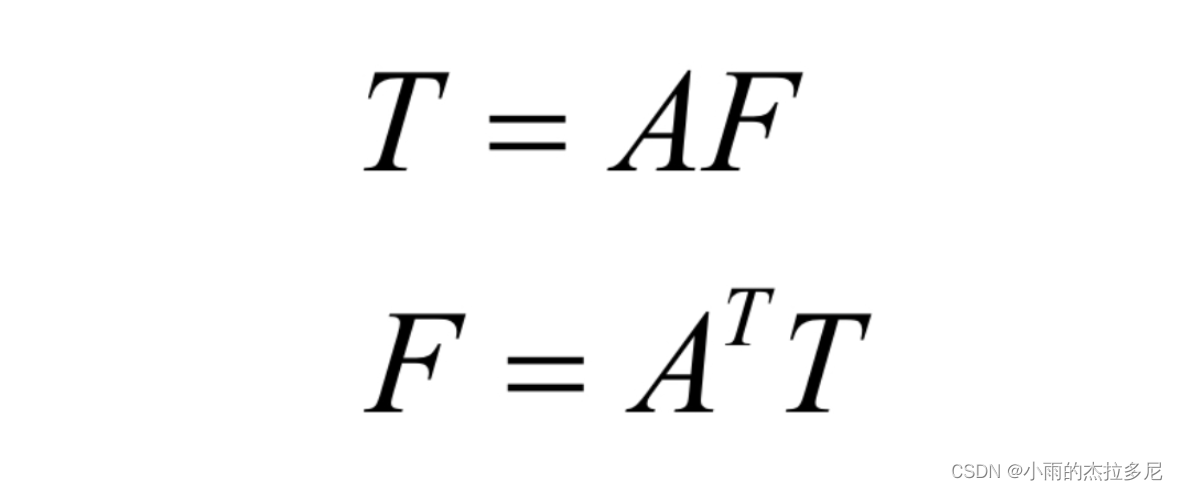
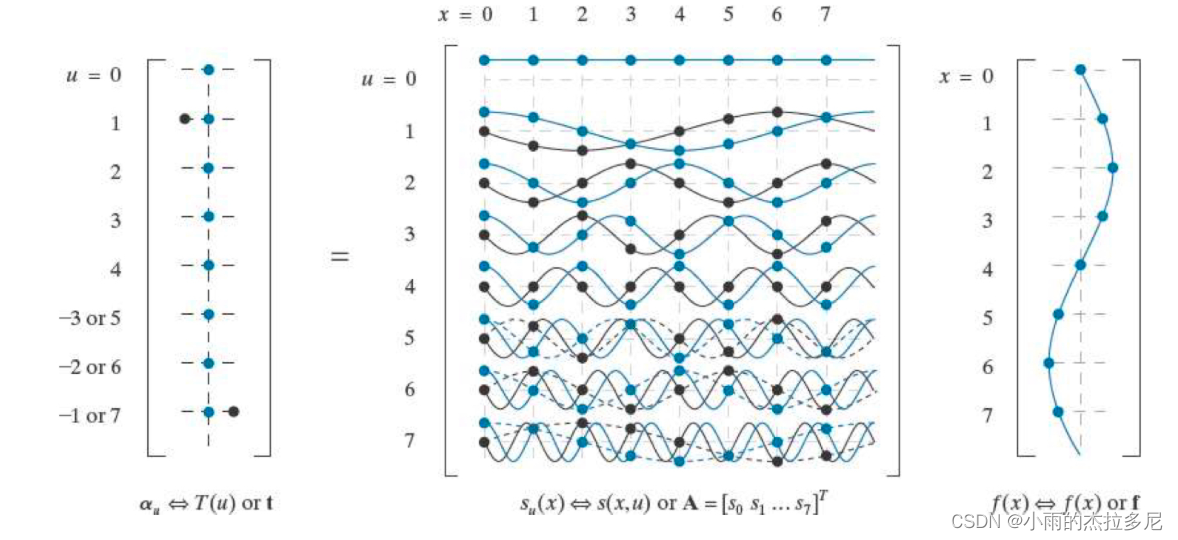
8.2 二维傅立叶变换

基图像:
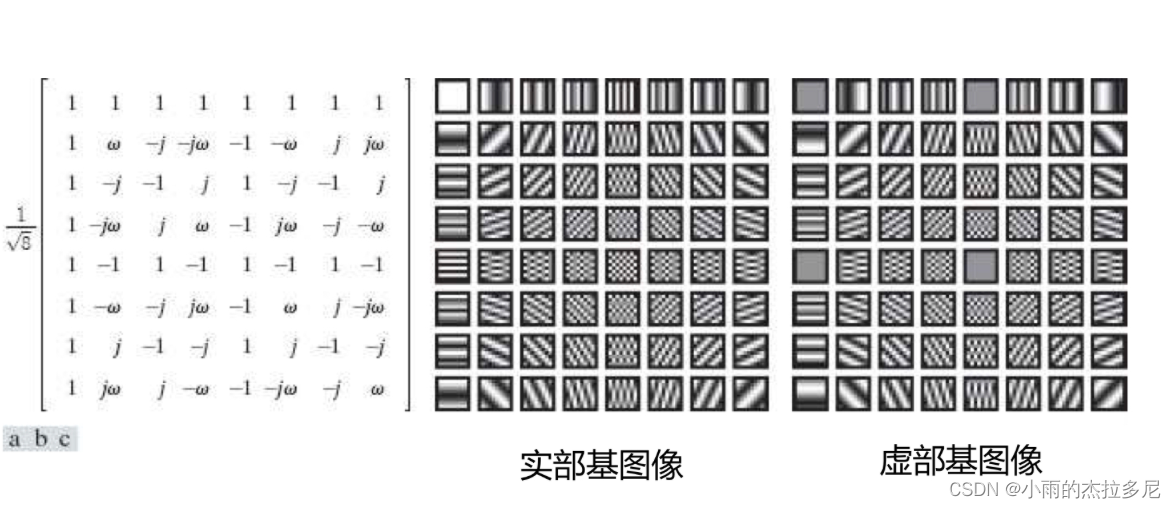
其他的:
- Hartley变换(与傅立叶变换相似,替换掉了复指数函数)
- 离散余弦、离散正弦变换
- Walsh-Hadamard变换,Slant变换,Haar变换
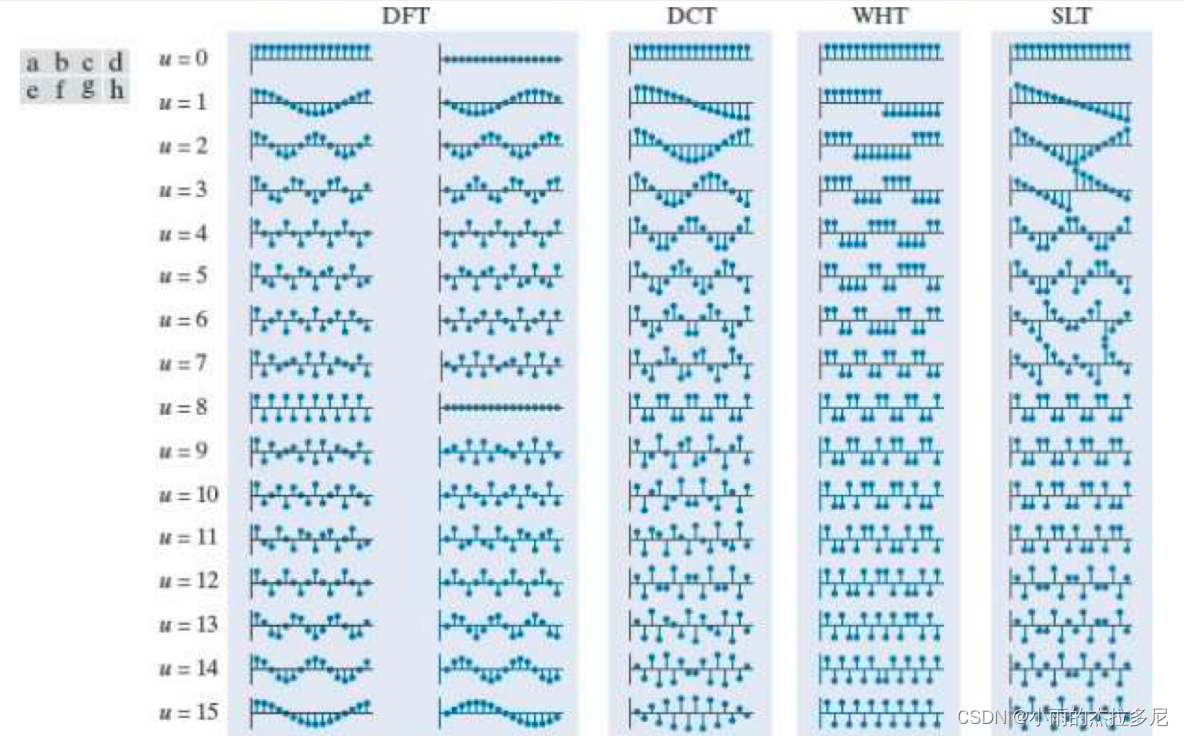
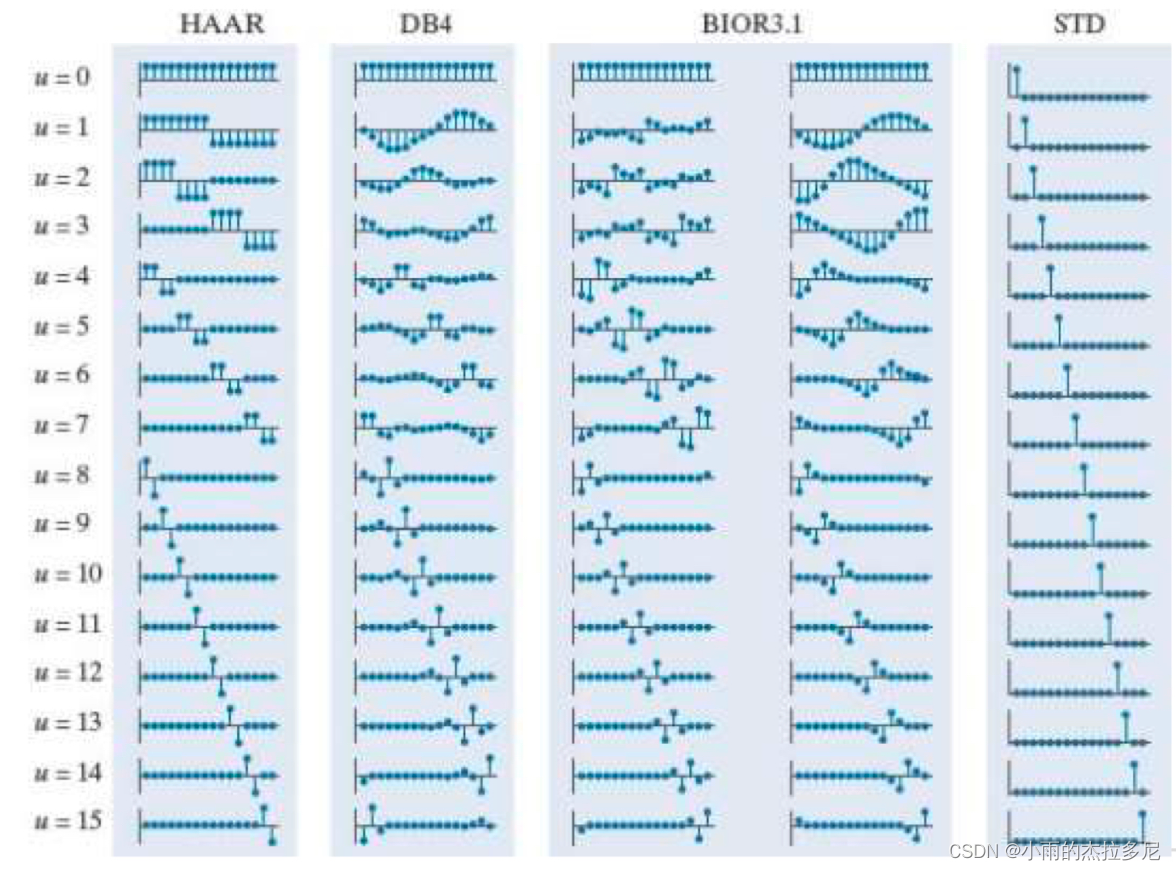
9. 距离变换
就是得到每个像素距离边界的最短距离。
欧氏距离、街区距离、棋盘距离
Hausdorff距离:两个边界,到彼此最小距离的最大值,然后再取max
距离变换局限性:对noise很敏感(可用形态学先去除噪声)
三、图像的统计描述
3.1 特征值、奇异值分解
奇异值分解:与特征值分解不同,是对于
A
T
A
A^TA
ATA
的特征值所作出的分解。

可以看作多个low-rank矩阵的加权和,权重就是对应的奇异值。
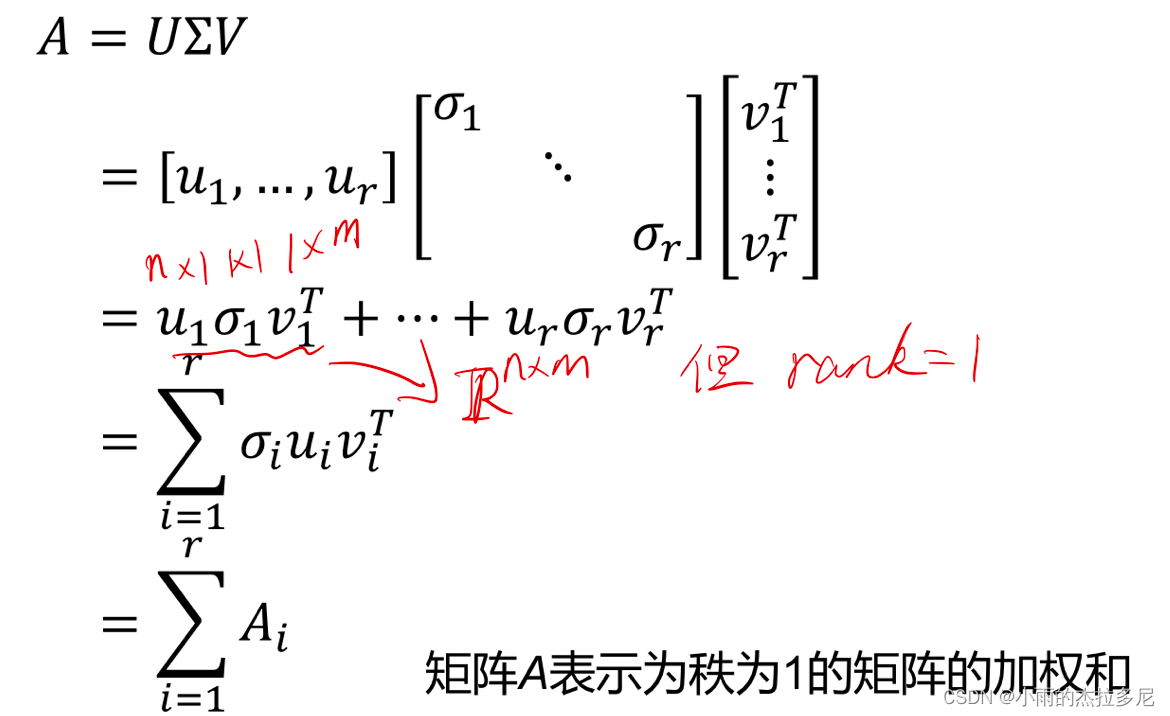
应用:最优逼近、图像压缩、denoising
3.2 图像的空间、统计描述
1.空间描述:邻域等
区域R的边界是指其R与R补集相邻的点集合。
2.统计描述:
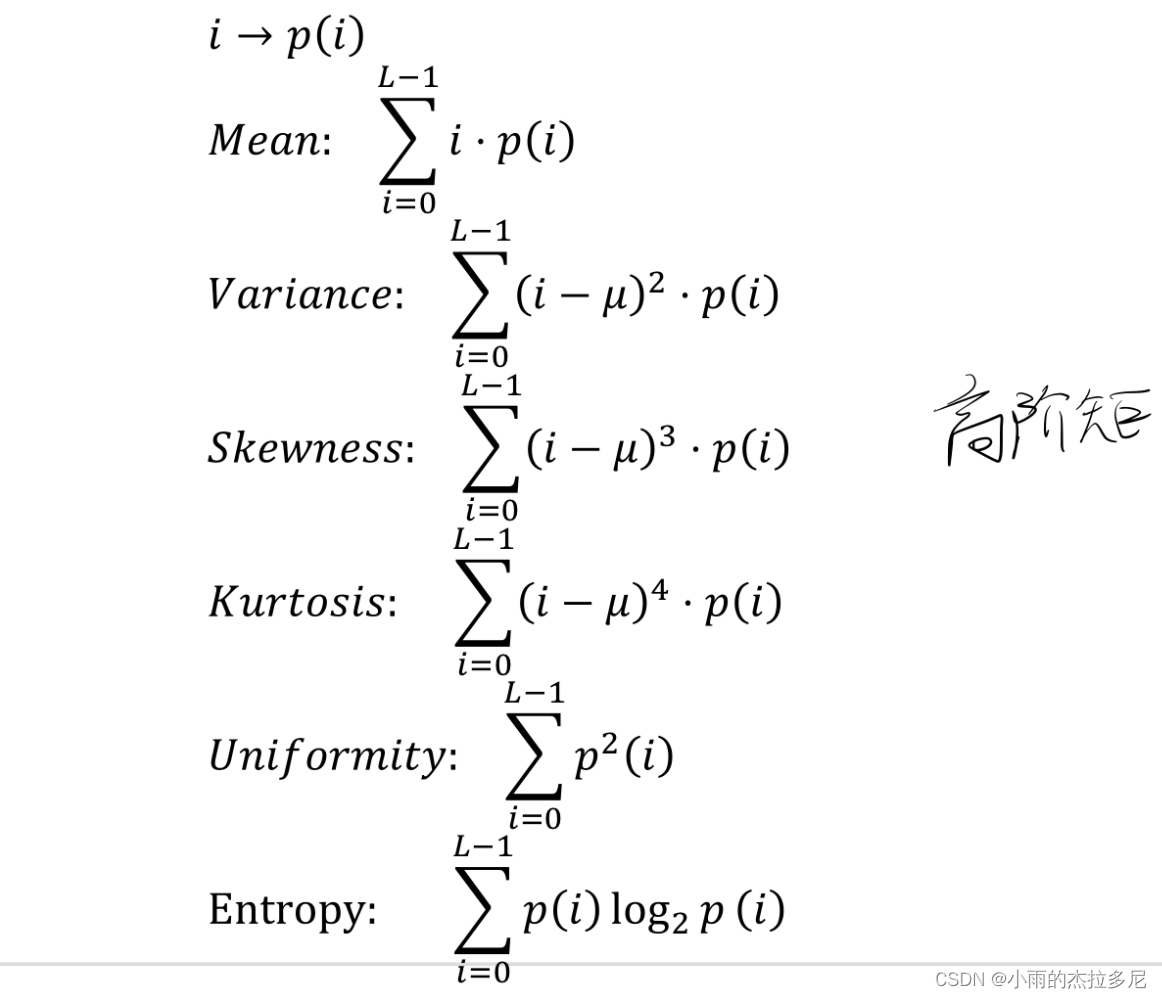
co-occurrence matrix:记录了出现图像变化的固定特征。
3.3 随机过程
概念:

马尔可夫链:
只和上一阶段的状态有关,与再之前的状态无关。
3.4 随机场
通过
场
来描述像素间关系。
MAP,后验就是已经有了当前像素的特征向量f,去估计其标签w。

MRF:概念
当前像素的类别只依赖于其邻域
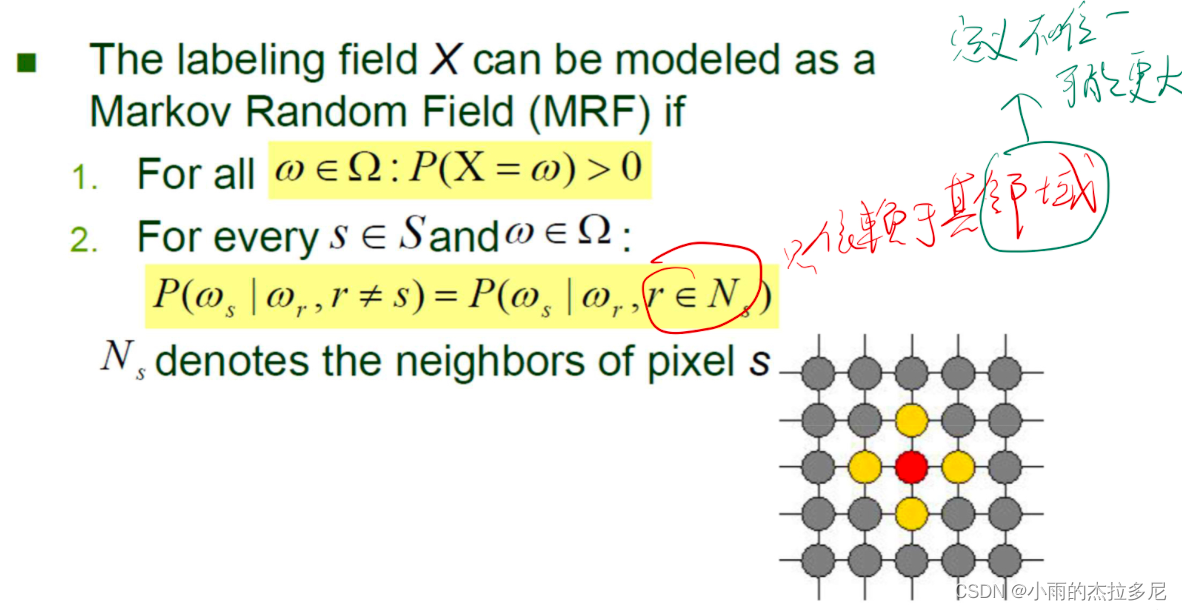
其中,likelihood假设服从高斯分布。
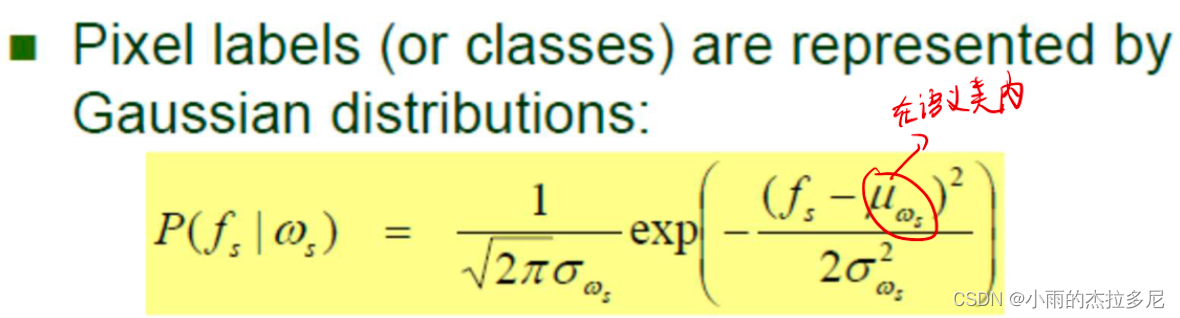
关于先验p(w),利用团势能来构建

四、图像增强
1. 线性灰度变换
就是成比例,对应即可
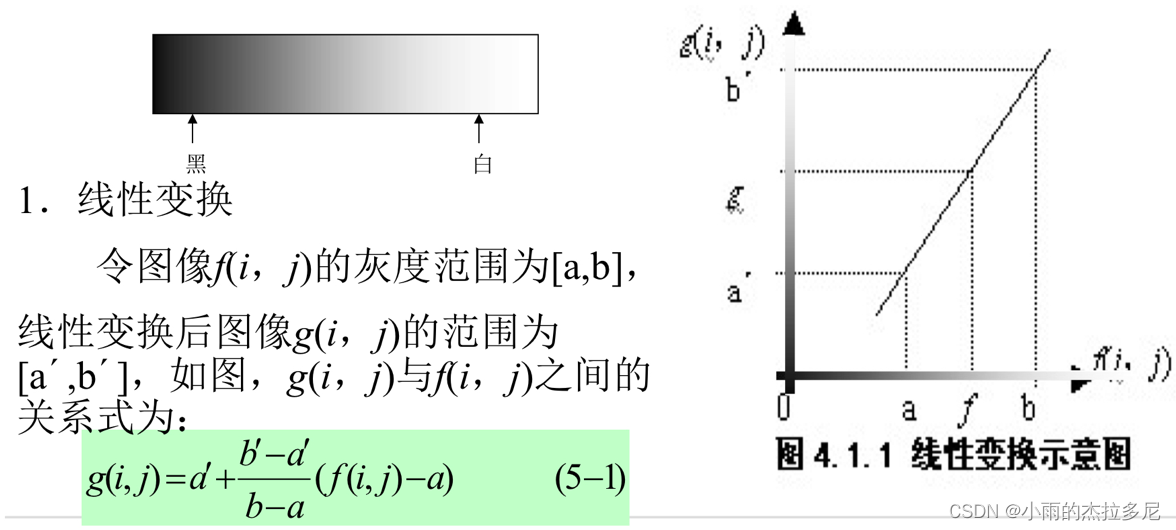
2. 非线性灰度变换
对数变换
g
(
i
,
j
)
=
a
+
l
n
[
f
(
i
.
j
)
+
1
]
b
⋅
l
n
c
g(i,j)=a+\frac{ln[f(i.j)+1]}{b·lnc}
g(i,j)=a+b⋅lncln[f(i.j)+1]
指数变换
g
(
i
,
j
)
=
b
c
[
f
(
i
,
j
)
−
a
]
−
1
g(i,j)=b^{c[f(i,j)-a]}-1
g(i,j)=bc[f(i,j)−a]−1
3. 直方图
3.1 直方图均衡化

3.2 直方图规定化
变成规定形状,突出某些灰度级(是要先做直方图均衡化)
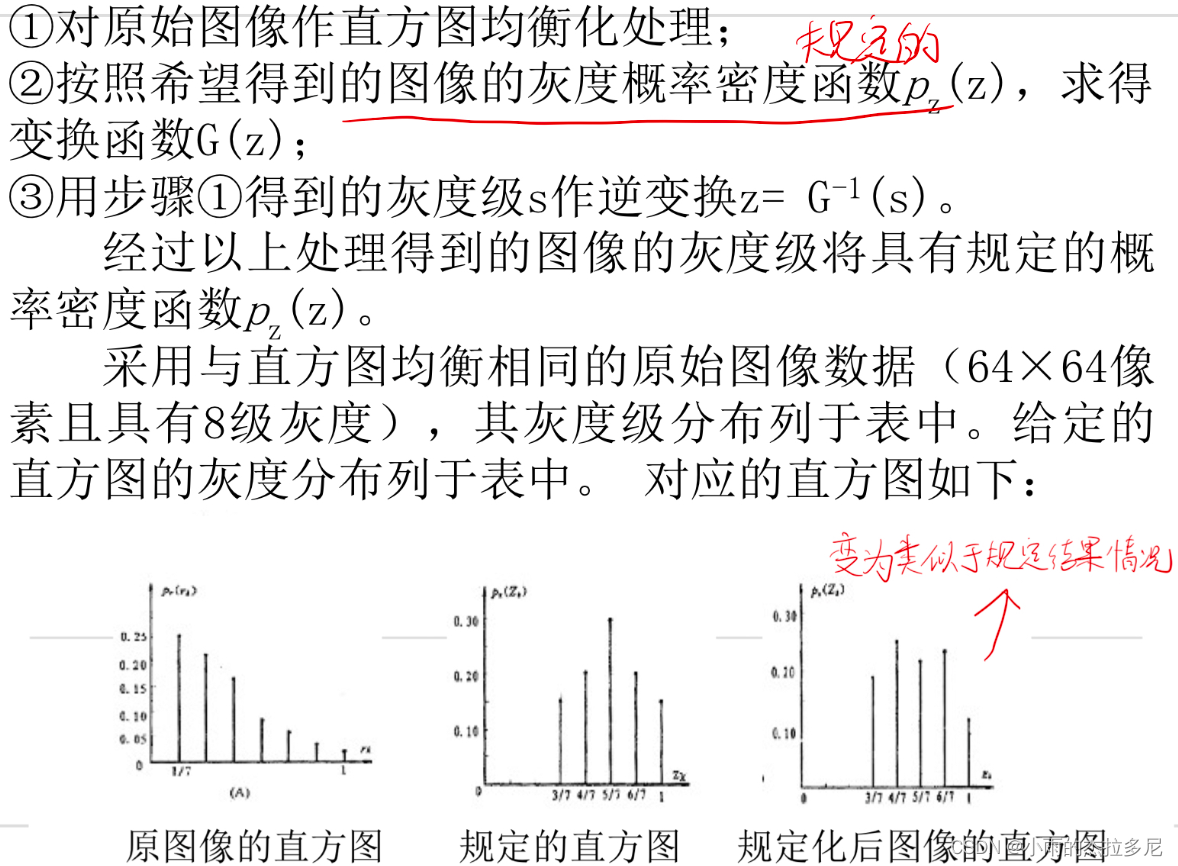
4. 彩色图像增强
伪彩色和假彩色增强区别:伪彩色是针对灰度图像处理,而假彩色是针对彩色图像处理的。
4.1 伪彩色
- 密度分割法:变换出的彩色数目有限
- 灰度-彩色变换合成法:三个通道按照比例合成不同颜色
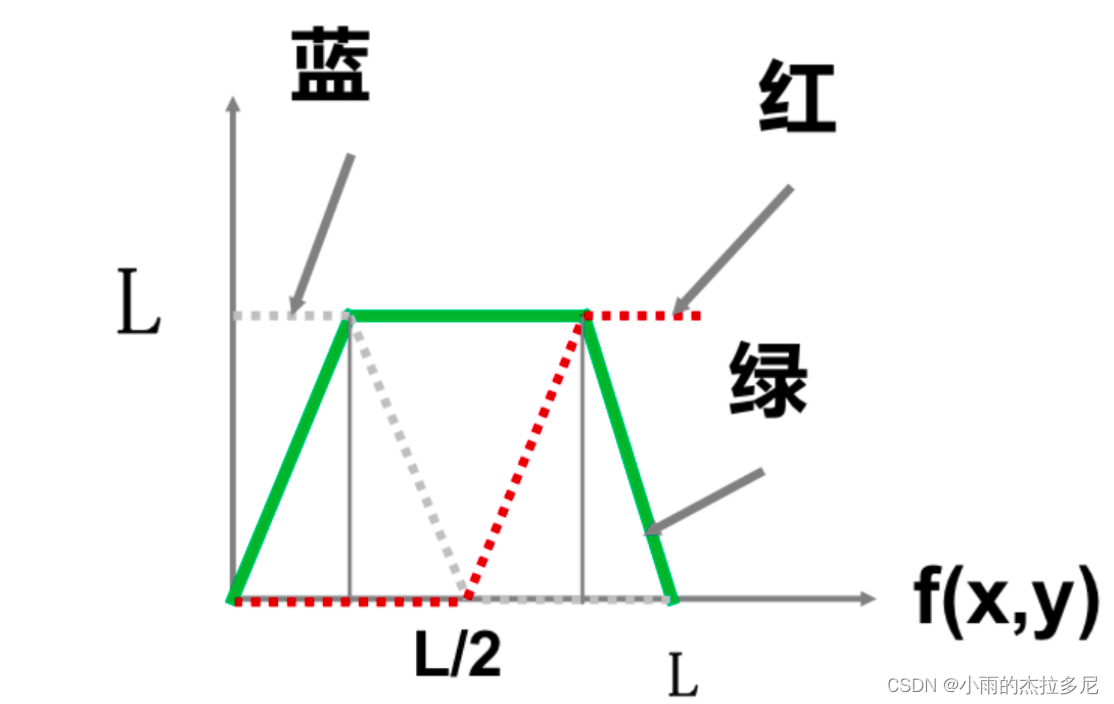
- 频率域伪彩色增强
4.2 假彩色
目的:突出感兴趣目标、呈现匹配的颜色
主要是多通道的线性变换
4.3 真彩色
RGB变为HIS,再增强某个分量,再变回RGB
5. 代数运算
相加:多个带noise图像相加,得到清晰图像
相减:去除背景、观察运动图像
相乘:mask
六、形态学处理
结构元:用来探测图像的小图像
1. 膨胀 & 腐蚀
膨胀
- 【映射后】结构元和原图像做与(相当于直接做卷积),如果有重叠则为1。
- 位移得到的所有图像取并。
腐蚀
- 结构元和原图像做与(相当于映射后卷积),如果完全重叠为1。
- 【映射后】位移得到的所有图像取交。
(A腐蚀B)补 = (A补)膨胀(B反射)
2. 开、闭运算
开就是先腐蚀再膨胀(能够让突出的部分变平滑)
闭就是先膨胀再腐蚀(能够让断裂的部分变连续)

3. hit & miss
击中击不中就是要找到恰好是当前结构的。
因此要正着腐蚀一次,反着腐蚀一次,求交集(都腐蚀到才算是找到了)。
4.应用
4.1 边界提取
原图减去腐蚀(腐蚀掉的部分就是边界)
4.2 区域填充
在要填充部分的内部找一个seed,然后每次膨胀一次与A补求交。循环多次后再与A并
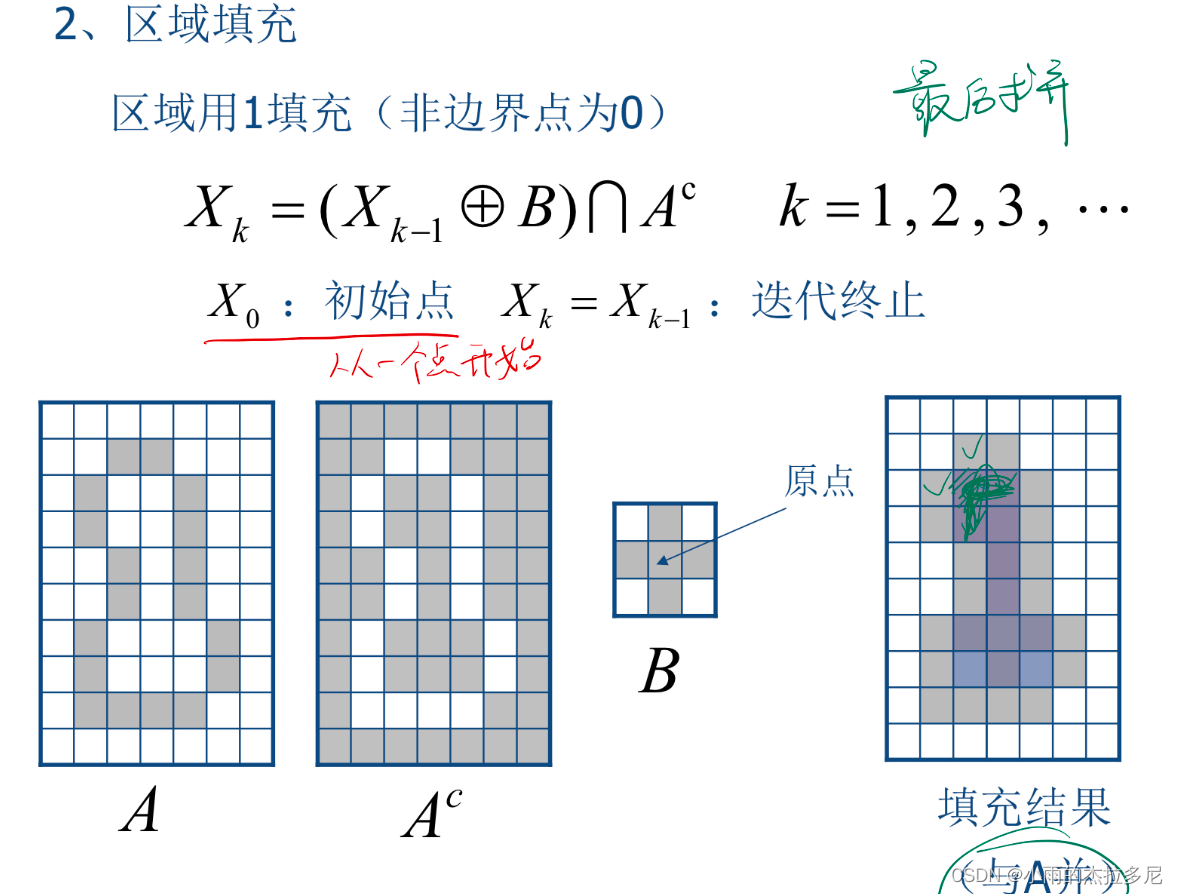
4.3 连通分量提取
和区域填充类似,只不过每一次是与原图像求的交集。就可以遍历得到连通分量。
4.4 凸包
每一轮分别用所有结构元进行hit&miss,直到不再变化。然后将每个结构元得到的结果求并。
4.5 细化 & 粗化
遍历所有结构元,在原图减去击中的部分。重复遍历所有结构元,直到图像不再变化。
粗化:每次并上击中的部分。直到不再变化
4.6 骨架提取
- 形态学提取前两列相减得到第三列,对每一次的结果求并。
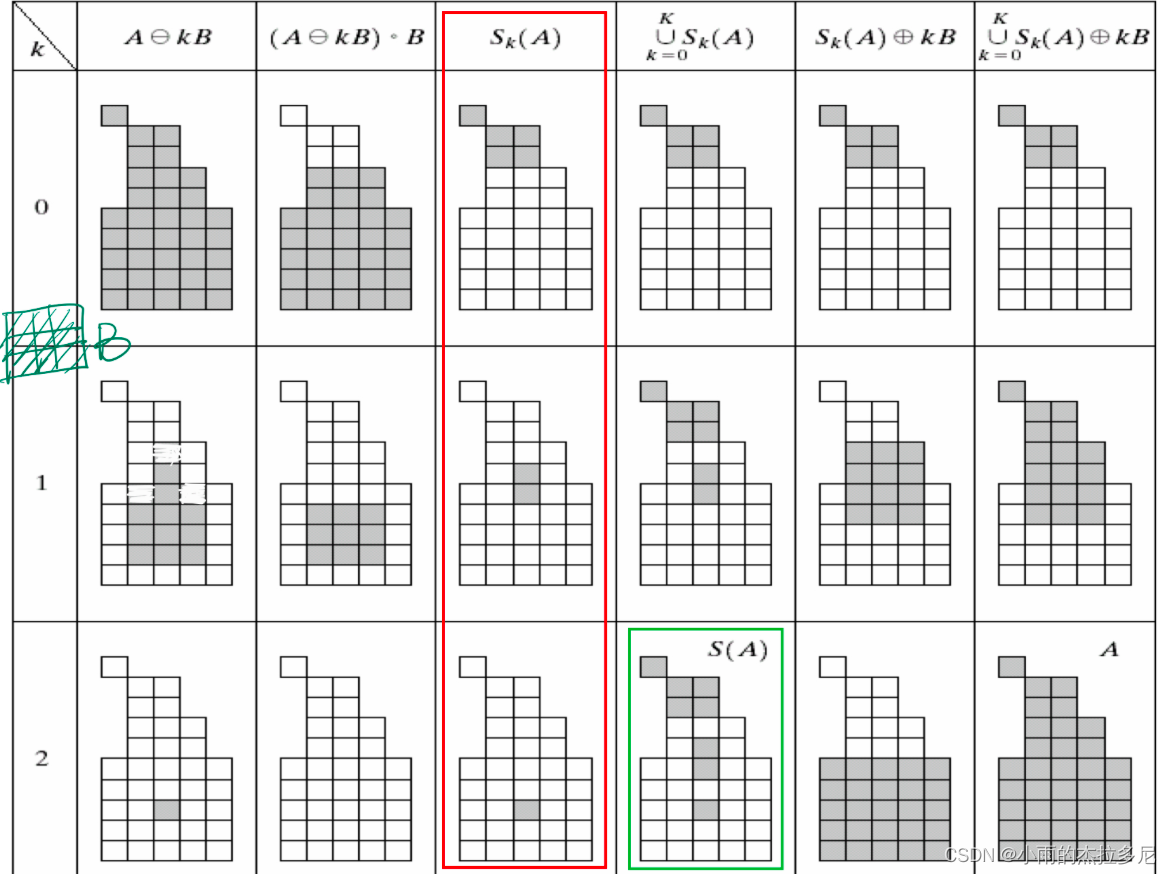
- 基于距离变换1. 提取图像边界(腐蚀一次取掉的部分)2. 对边界二值图求距离变换3. 距离变换的局部极大值4. 与原图像求交集得到骨架其中局部极大值的部分最好是用可以与四周取等的结果来做(不要严格大于)。具体的距离变换过程:就是用这样第一个模版,从左上向右下遍历一次。另一个模版右下到左上遍历一次。

4.7 裁剪
目的就是去掉二值图中小的毛刺。
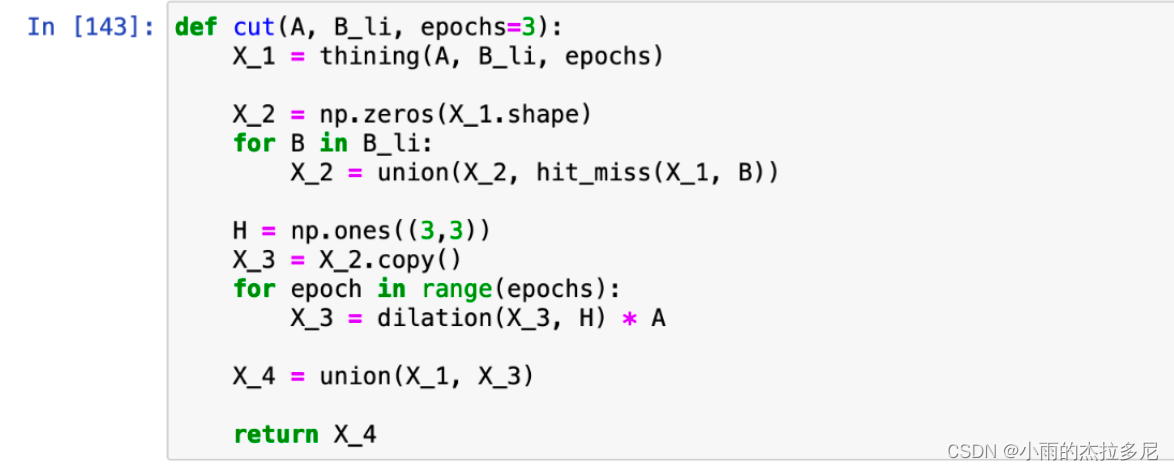
5. 灰度图形态学
膨胀:用求最大值来代替求和
腐蚀:用求最小值来代替求和
开运算:就相当于用球在灰度线上滚(去峰值)
闭运算:就相当于用球在灰度线下滚(填坑)
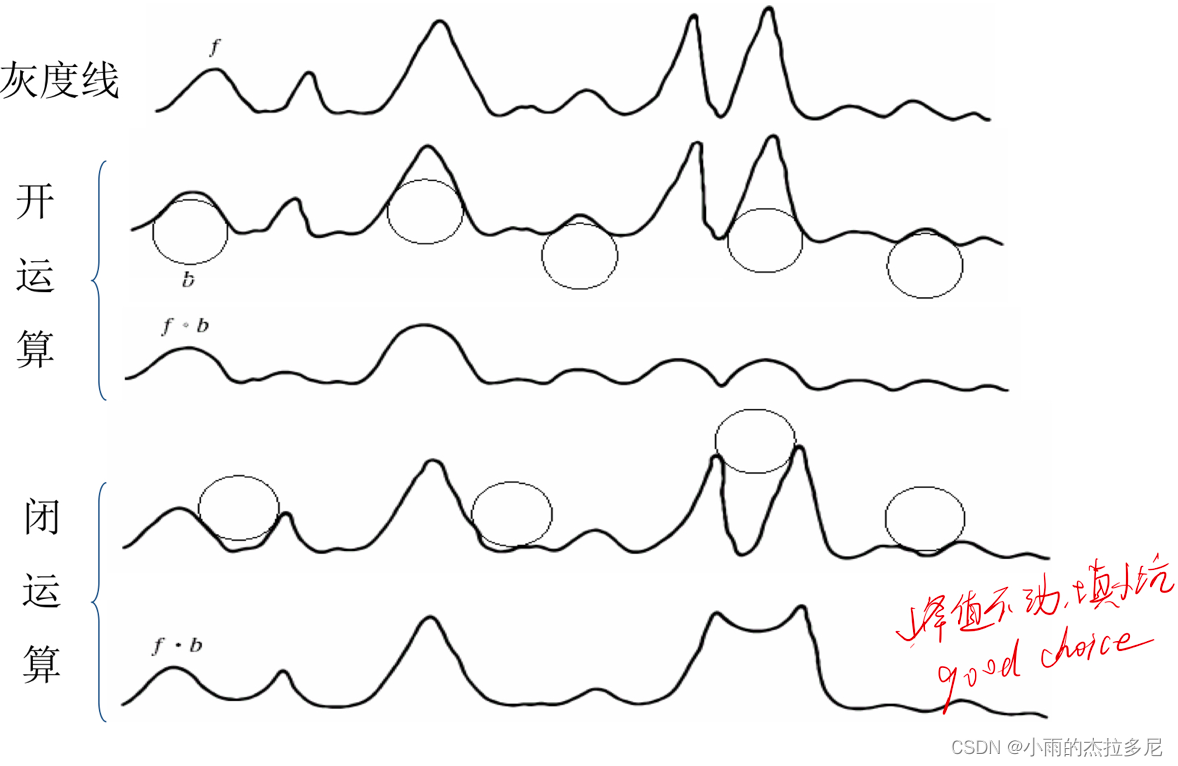
图像平滑:先开再闭
图像梯度:膨胀减腐蚀
高帽:原图减开运算,增强阴影细节(留下了峰值)
七、图像分割 & 边缘检测
1. 图像分割
把图像分成各具有同一特性的区域。
基于不连续性(边缘)、相似性(化为相似区域:阈值、区域生长等)
1.1 基于不连续性
1.1.1 奇异性检测
二维:孤立点、线、边缘
小波变换可以检测点、线、边缘的奇异性,可以解析并精确了解局部不连续性。可以检测奇异性、和其阶次。
点检测:
利用中心值增强的拉普拉斯模版滤波,响应值超过阈值的话,就相当于匹配上了。
线检测:
利用中间正,两侧负的模版,来检测线条。(平坦区域响应值是0)
边缘检测:
梯形是器械成像结果。
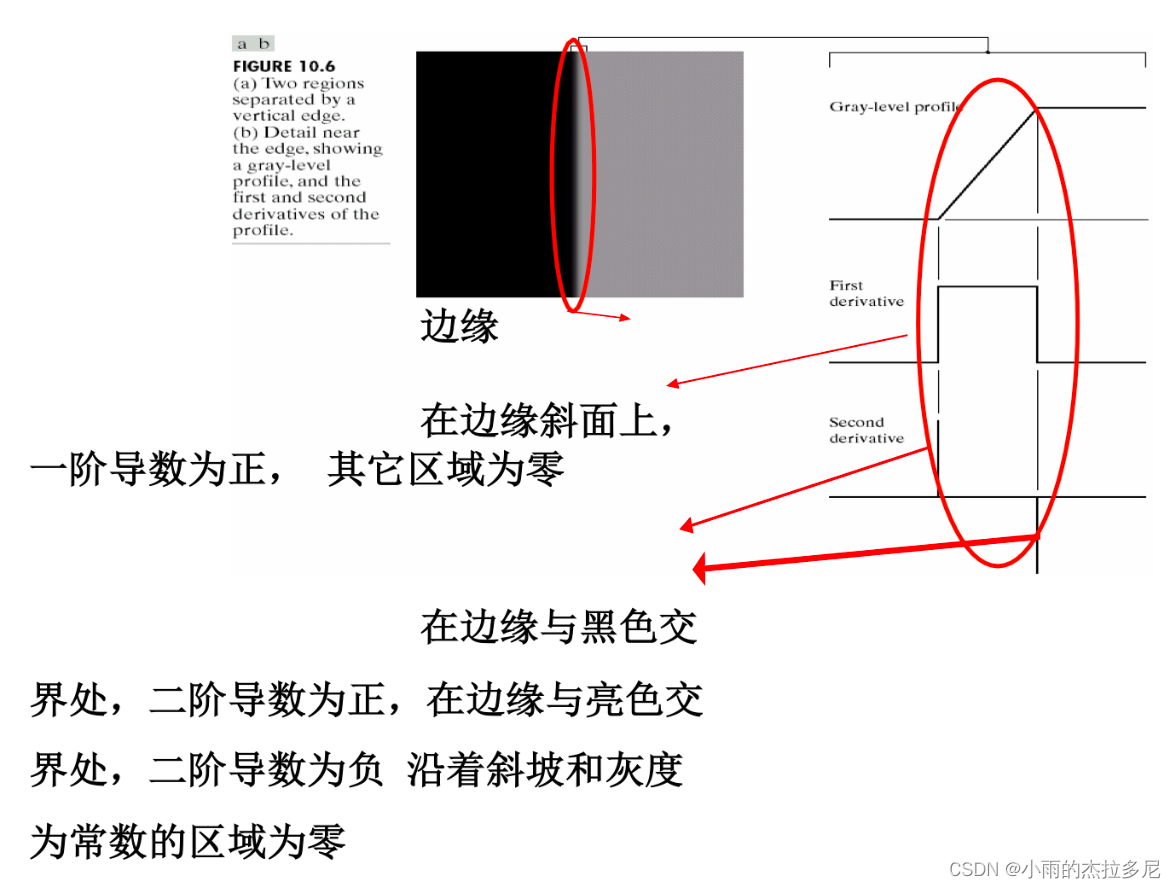
一阶导数:
- Roberts:2*2,适合处理边缘陡峭、噪声低的图像。
- Sobel和Prewitt:二者权值不一样,但都有噪声抑制能力。但出现宽边界
Canny算法步骤:
- 高斯滤波器平滑
- 计算梯度大小和方向
- NMS细化边缘
- 双阈值处理(大于hthr的一定是边缘,小于lthr的一定不是边缘,在他们之间的值如果和hthr边缘连接则算作边缘)
二阶导数(过0点就是边界):
- Laplacian算子(对noise敏感)
- LOG算子(先高斯,再Laplacian)【可能sharp边缘被扔掉】
- DOG(差分高斯函数简化LOG)
1.1.2 边缘连接、边界检测
需要将边缘连接完整(因为边缘必须连续且封闭)
- 可以利用梯度的垂直方向找寻边界,即局部处理。
- 可以用Hough变换进行全局处理
Hough变换:
相交直线越多,则xy直线更是我们的解。用极坐标就可以解决垂直问题(盲点)
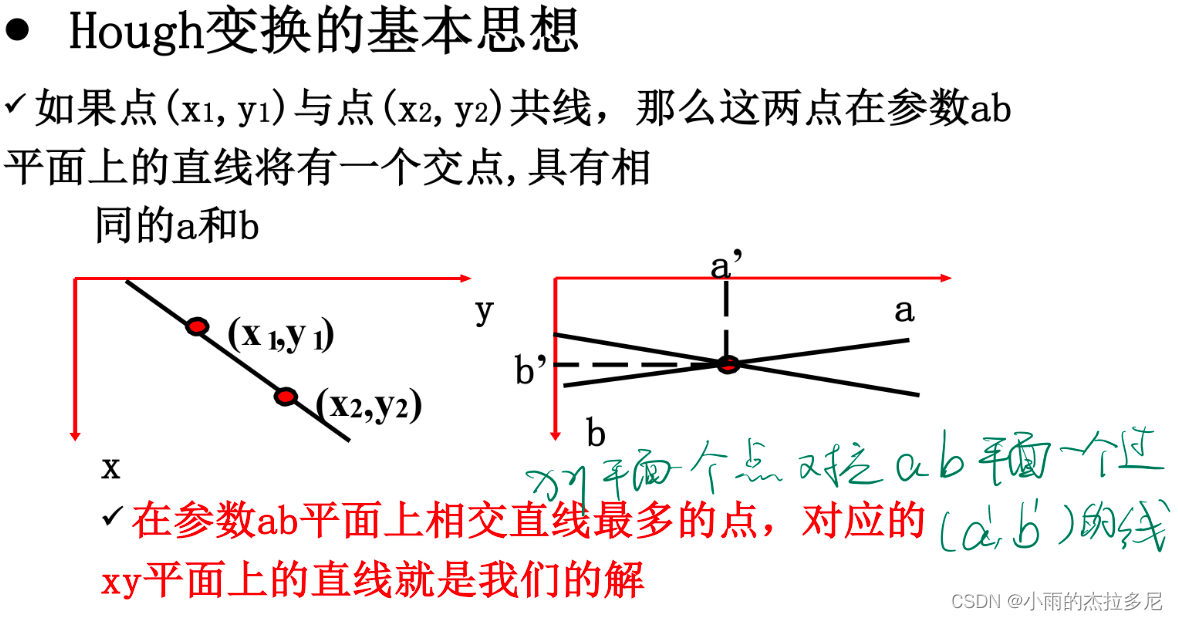
1.2 像素性质(阈值处理)
方法分类:阈值T仅取决于灰度值,则全局阈值;取决于灰度值和局部性质,则局部阈值;取决于坐标xy,则自适应。
- 基本全局阈值:划分后,将两类的灰度平均值取平均,再重新划分。(解决不了不均匀亮度)
- 基本自适应(分片)
- 最佳阈值
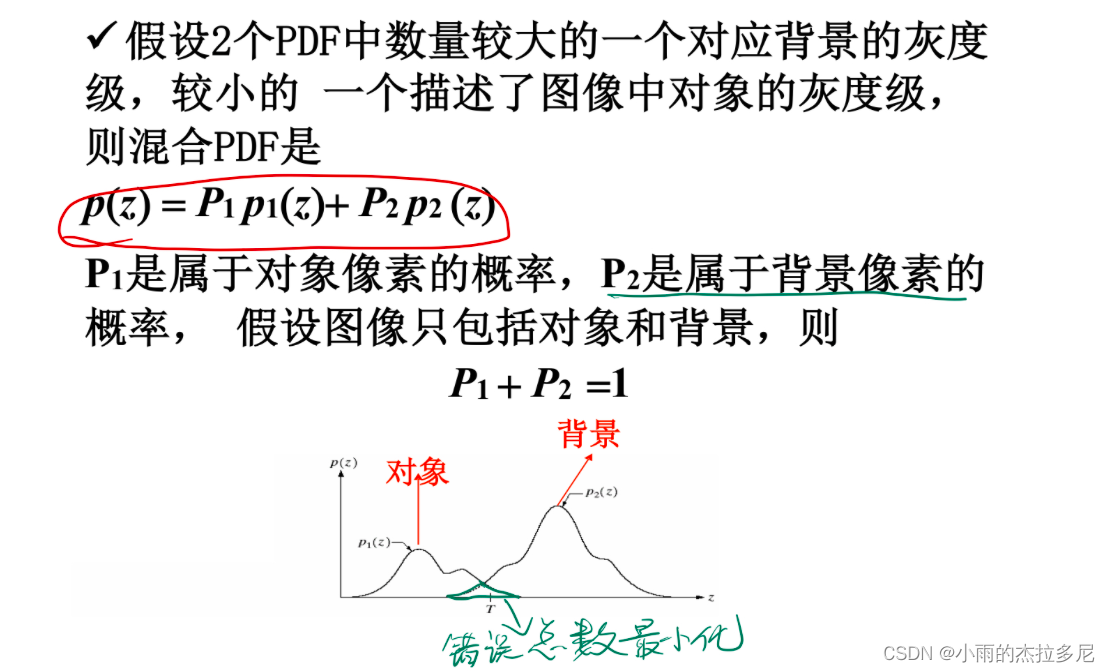
E1是背景像素被分为前景的错误率,E2是前景像素被分为背景的错误率
另外:如果此处两个概率密度函数都是高斯分布,则结果会怎样?(计算)
若两个sigma相同,则得到单一阈值;再此基础上,若先验P1=P2,则阈值为均值平均
- 边界区域选阈值改善直方图形状,不考虑内部像素优点:可以让两个波峰更加对称、高度接近(不受区域内外的像素个数影响)
1.3 搜索区域(基于区域)
- 区域生长(种子像素,和并周围相似的像素)
- 四叉树分解(划分原图像为4块,如果不满足一致性,则继续分裂成4块。满足了的块就停止。最后所有块都满足一致性。)
- 平均灰度方法
- PDE方法(连续微分算子代替离散滤波、提取的边缘闭合)
- 活动轮廓模型(转化为曲线的能量最小化问题,其中第一项积分代表弧长,第二项代表振荡,第三项是负梯度相关。也就是要让曲线:短+光滑+过梯度大的点)
版权归原作者 小雨的杰拉多尼 所有, 如有侵权,请联系我们删除。