点击上方“Deephub Imba”,关注公众号,好文章不错过 !
在这篇文章中,我将解释有监督的机器学习技术如何相互关联,将简单模型嵌套到更复杂的模型中,这些模型本身嵌入到更复杂的算法中。接下来的内容将不仅仅是一份模型备用表,也不仅仅是一份监督方法的年表,它将用文字、方程和图表来解释主要机器学习技术家族之间的关系,以及它们在偏差-方差权衡难题中的相对位置。

嵌套模型示例:错误概率密度 < 线性回归 < 逻辑回归 < 前馈神经网络 < 卷积神经网络
从文氏图(Venn Diagram)到最简单的机器学习模型
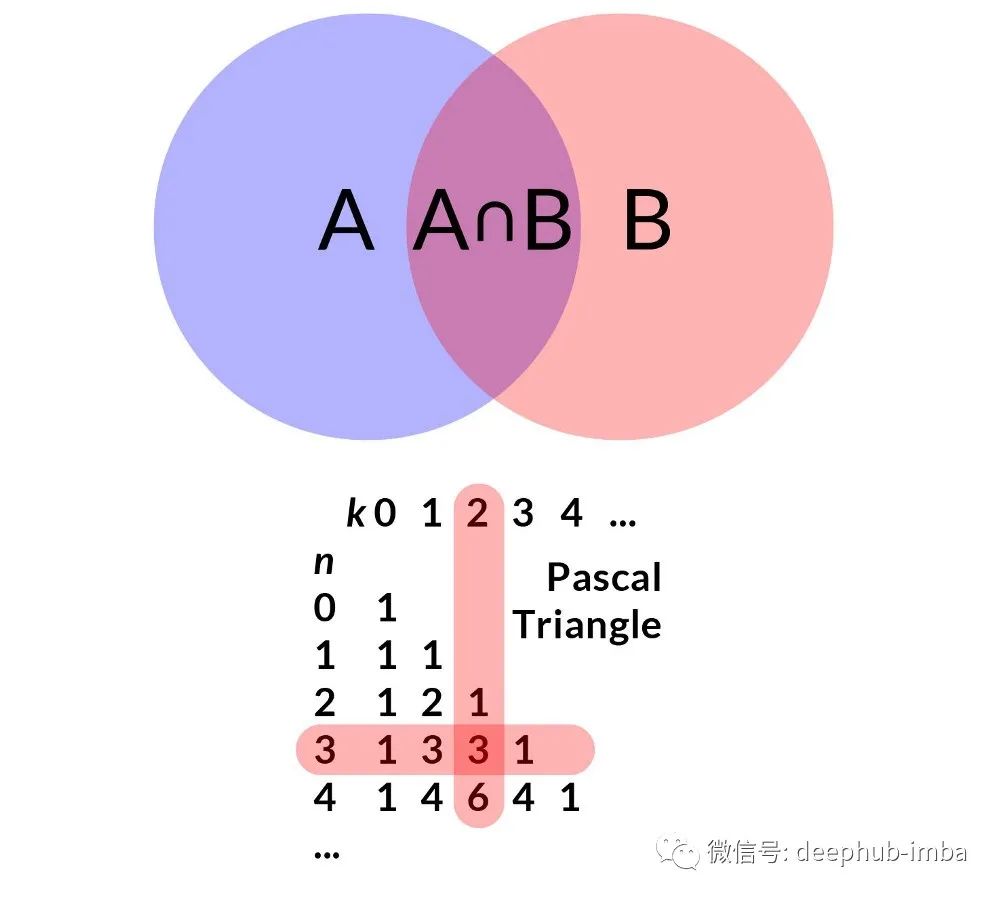
回顾机器学习技术的历史我们首先看到的就是概率论。概率论可以从 Kolmogorov 公理或简单地从文氏图中导出。这在 McDowell 的“Cracking the Coding Interview”中得到了最好的解释。我们有两个事件 A 和 B。两个圆圈的面积代表它们的概率。重叠区域是事件{A and B}。我们直接得到 P(A and B) = P(A)×P(B given A) 因为我们需要事件A和事件B同时发生(假设A已经发生)。A 和 B 是可以互换的,所以我们也有 P(A and B) = P(B)×P(A given B)。我们通过结合这两种关系得到贝叶斯定理:P(A|B) = P(A)×P(B|A) / P(B)。这就是朴素贝叶斯分类器最基础的理论。
现在,事件 {A or B} 的概率是多少?在文氏图上,我们观察到它是 A 的面积和 B 的面积之和。然而为了避免重叠面积的重复计算,我们有 P(A or B) = P(A) + P (B)-P(A and B)。正如我们看到,AND 和 OR 这两个逻辑关系导致二项式分布,然后是正态分布,这就是线性回归的基础。
让我们深入研究一下。二项分布的形式为
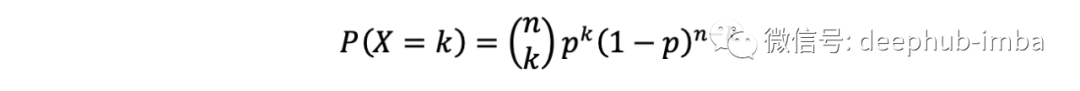
也就是在n个独立的伯努利试验中恰好有k次成功的概率
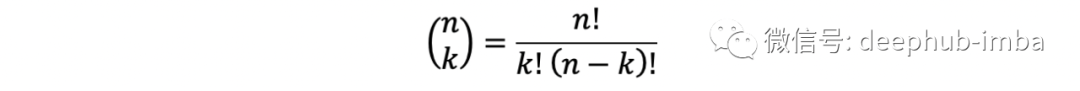
由杨辉三角描述(见上图)。这看起来很复杂。然而,它可以很容易地从文氏图推导出来。独立伯努利试验意味着事件 A 和 B 是独立的,因此 B 不以 A 为条件,A 也不以 B 为条件。从上面可以得出 P(A and B) = P(A)×P(B),或在本实验中,P(A k times and not A (n-k) times) 等于 p^k* (1-p)^(nk)(因为 A 和非 A 的总和必须为 1)。如果我们拿一枚硬币,有 k 个正面(事件 A)和 n-k 个反面(事件 B,即不是 A),有不同的方法来实现这样的事件,用二项式系数表示。例如,在 n = 3 次试验中取得 k = 2 次成功,我们可能有 {H, H, T}, {H, T, H} 或 {T, H, H}。所有这些路径都是互斥的,给出 P(A' or B') = P(A') + P(B'),或 3 * p^k * (1-p)^(nk),这就是二项分布!如果n取足够大的时候,就是正态分布。
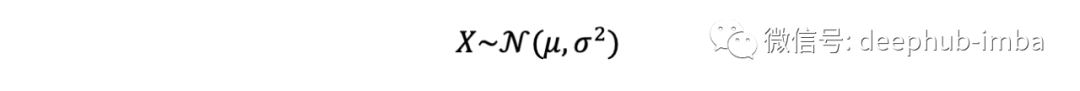
是具有均值 np 和方差 np(1-p) 的二项式分布的一个很好的近似值。
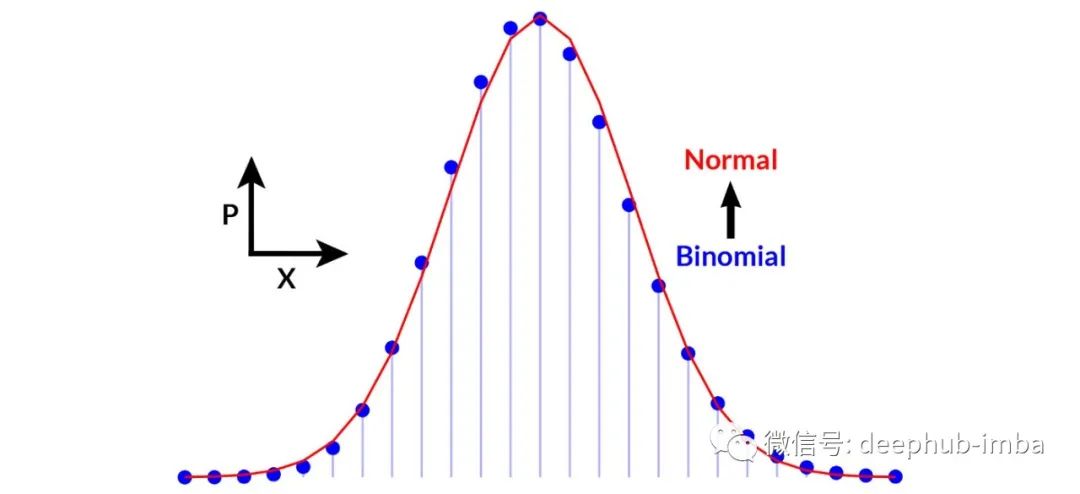
在n非常大,p非常小时的二项分布(离散)和正态分布(连续)
这就是机器学习和统计学的主力是线性回归
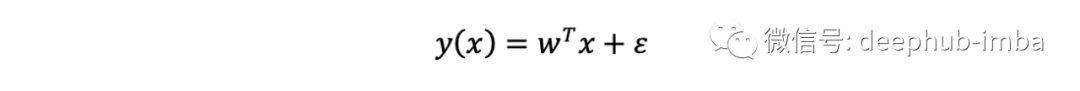
为了训练这个模型,要最小化的误差函数是残差平方和(观测值和预测值之间的差)。正是高斯在19世纪早期成功地将最小二乘方法与概率原理和正态分布(带有残差的高斯误差)联系起来。在线性回归的概率公式中,正态分布和线性回归之间的联系变得清晰起来:
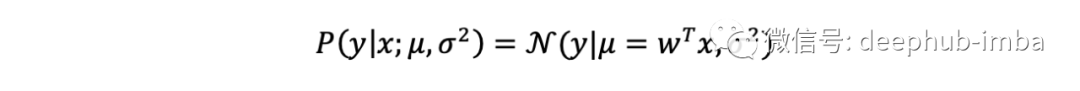
注意我们是如何仅从一个简单的文氏图就达到这个阶段的!
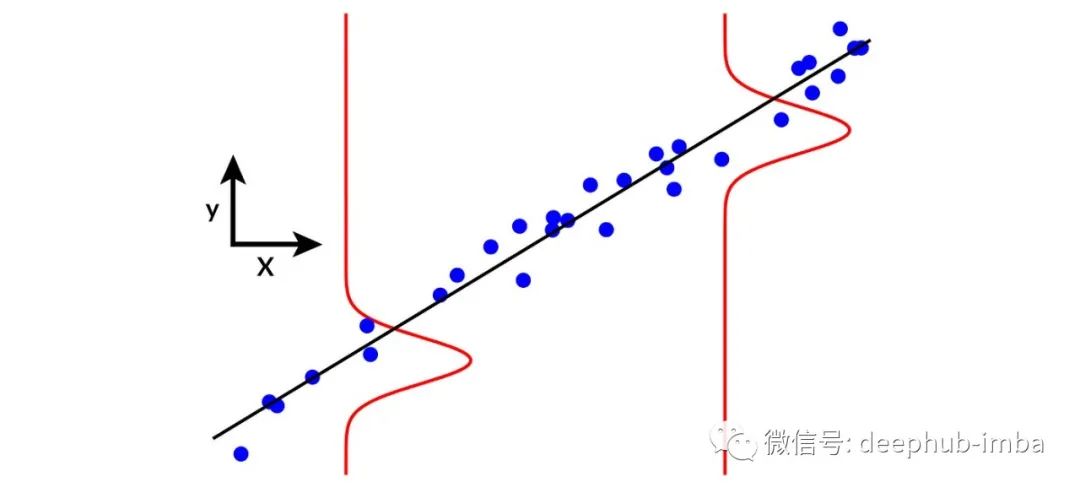
带有噪声正态分布的线性回归。
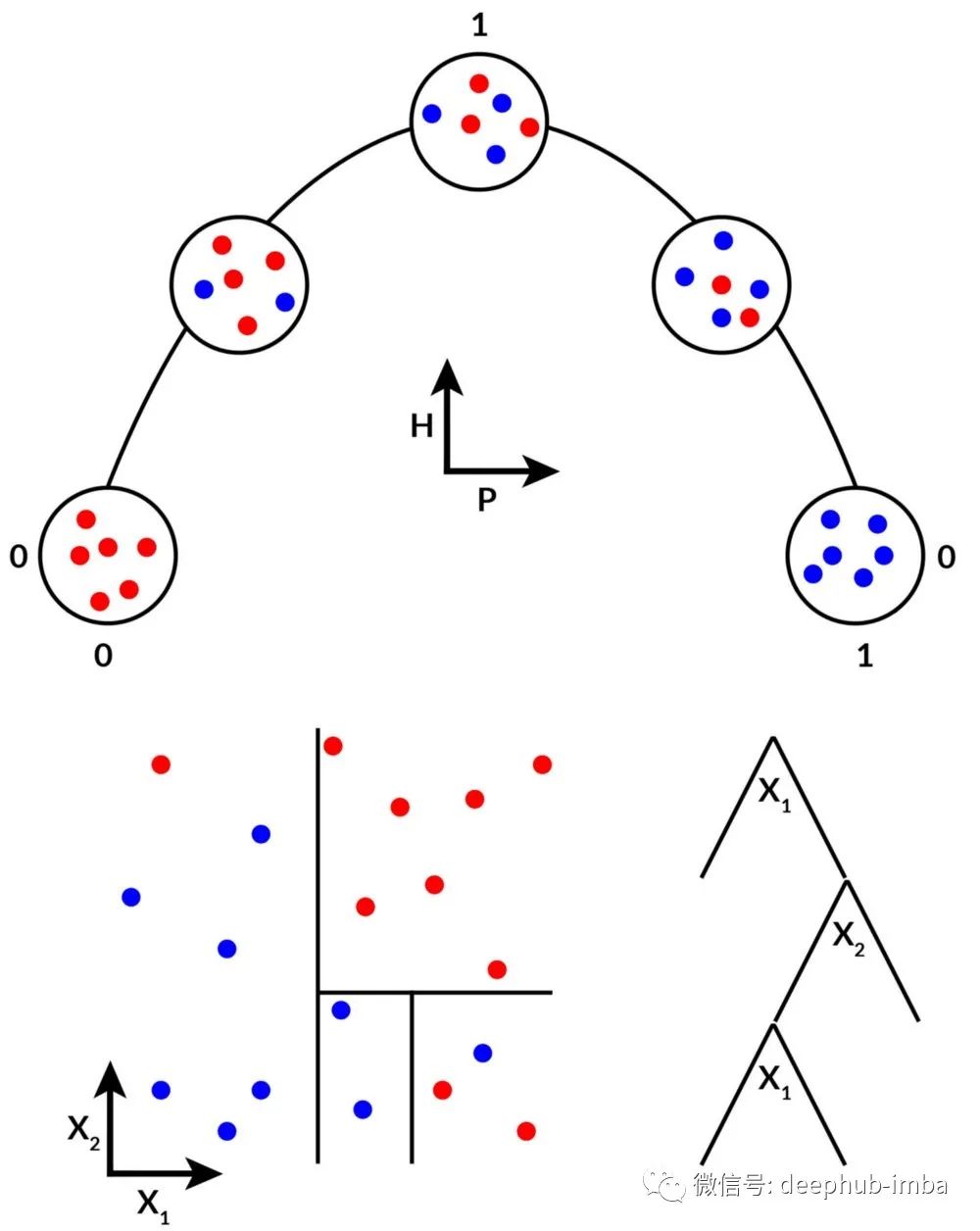
让我们回到概率论来查看另一个分支。香农在 1948 年将熵 H 定义为 -p_i×log_2[p_i] 的总和,这是一种纯度度量。取两个类 y = (🔴,🔵),集合 { 🔴, 🔴, 🔵, 🔵, 🔴} 的熵增加 x 是 -p(🔴)×log_2[p(🔴)]-p(🔵)× log_2[p(🔵)] 在这里表示为 -3/5×log_2[3/5]-2/5×log_2[2/5]≈0.97,这是非常不纯的(信息熵越小,就说明不确定性越低,确定性越高,纯度越高)。决策树在给定的 x 处进行拆分,以便最小化 2 个子集的组合熵,即 {{ 🔴, 🔴}, { 🔵, 🔵, 🔴}}。这是通过信息增益的概念来完成的,信息增益就是条件确定的情况下,信息的不确定性减少的程度。也就是说按照条件对数据进行分类拆分之后,分类数据的确定性是否比划分之前更高。同样在这里这里0.97-(2/5×[-1×log_2(1)] + 3/5×[-1/3×log_2(1/3)-2/3×log_2(2/3)])≈0.42 ,这表明分裂所做的熵显着减少。为清楚起见,决策树拆分的目标是最大化信息增益。这在 Provost & Fawcett 的《Data Science for Business》一书中得到了很好的解释。通过装袋(自举法)和提升,可以开发一系列基于决策树的技术,包括随机森林和提升树。
从线性回归到其他一切!
现在让我们从线性回归分支扩展进化。首先结合线性回归和贝叶斯定理产生了几种机器学习技术。这在Murphy 2012 年的“Machine Learning a Probabilistic Perspective”中得到了优雅的描述。让我们首先将贝叶斯定理重写为 P(Model|Observations) = P(Model)×P(Observations|Model) / P(Observations),或者换句话说,后验等于先验乘以被边际归一化的似然。线性回归以前被形式化为似然函数并省略了统一先验。而正则化技术(为了最小化过拟合):Ridge 模型其系数先验地服从正态分布,Lasso 模型其系数服从拉普拉斯先验分布。这些技术对非线性回归特别有用;所以,让我们添加基函数扩展的概念,从线性回归到非线性回归,例如多项式回归:
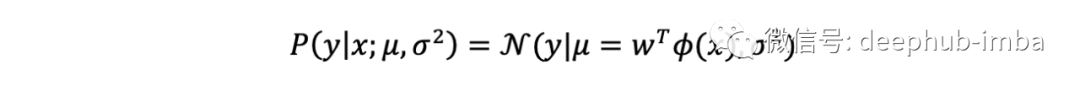
和
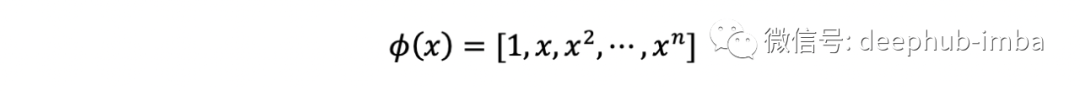
下图说明了多项式回归以及通过 Ridge 和 Lasso 进行正则化的作用。
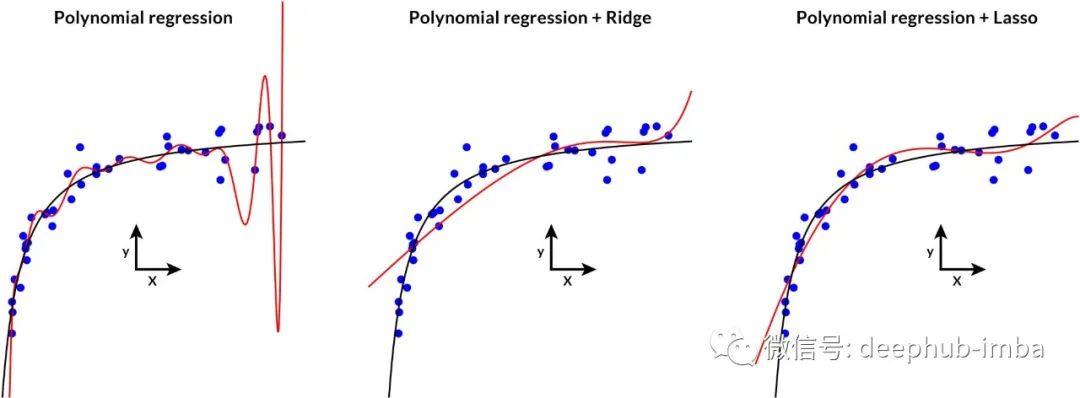
由 Ridge 或 Lasso 正则化的过拟合多项式回归
从线性回归中发展出的另外有两个机器学习系列是:支持向量机和人工神经网络。
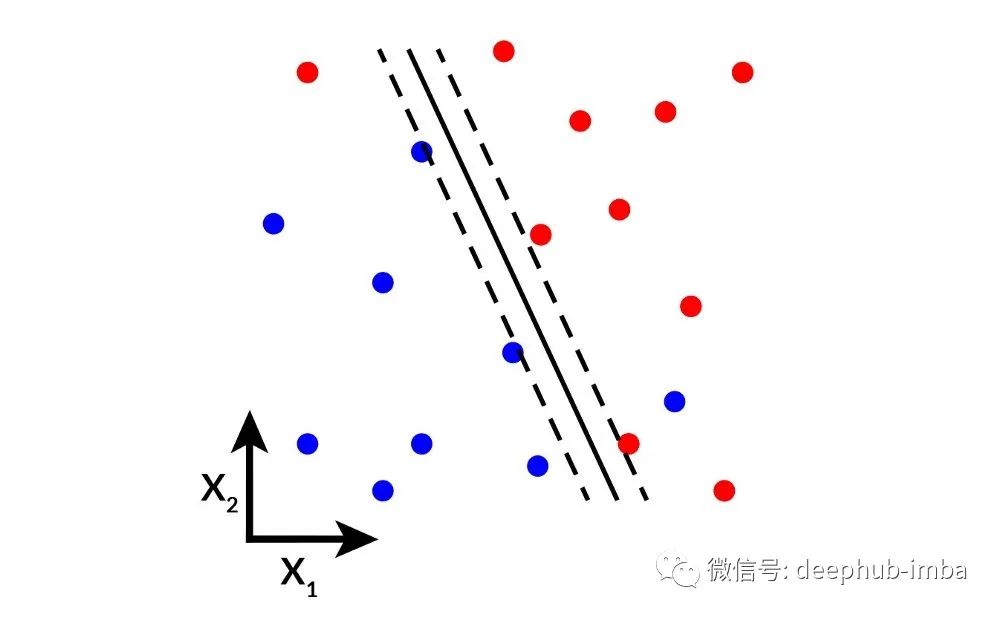
支持向量机 (SVM) 是一种线性模型,它通过所谓的最大边距超平面将两个类分开,可以写成满足以下等式的点集 x:
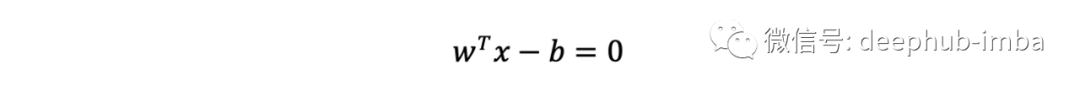
将两类数据分开以使它们之间的距离尽可能大的两个平行超平面定义为

上面两个公式被称为边距(margins)。无需深入研究 SVM 的细节,我们会立即看到与线性回归的联系。
回想一下,线性回归被定义为正态分布似然。如果我们现在用伯努利分布(二项式分布的特例)替换正态分布,我们就能得到逻辑回归:
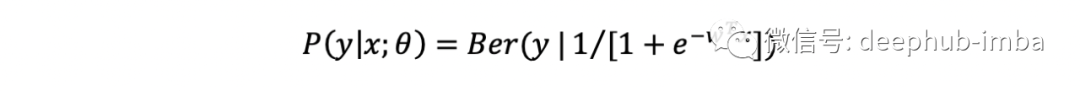
这里的线性回归是在 sigmoid 函数中实现的,以确保结果本质上是概率性的,即在 0 和 1 之间,使用类而不是连续值。
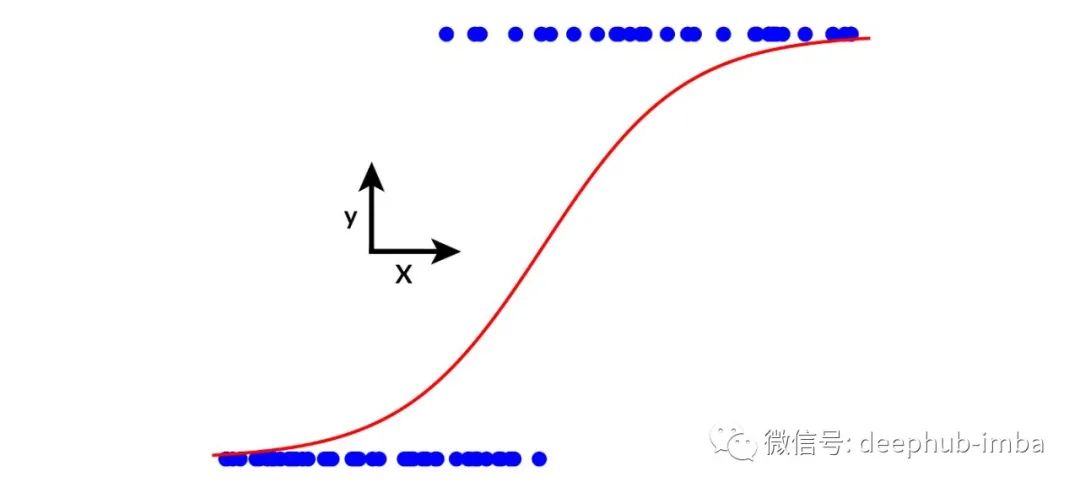
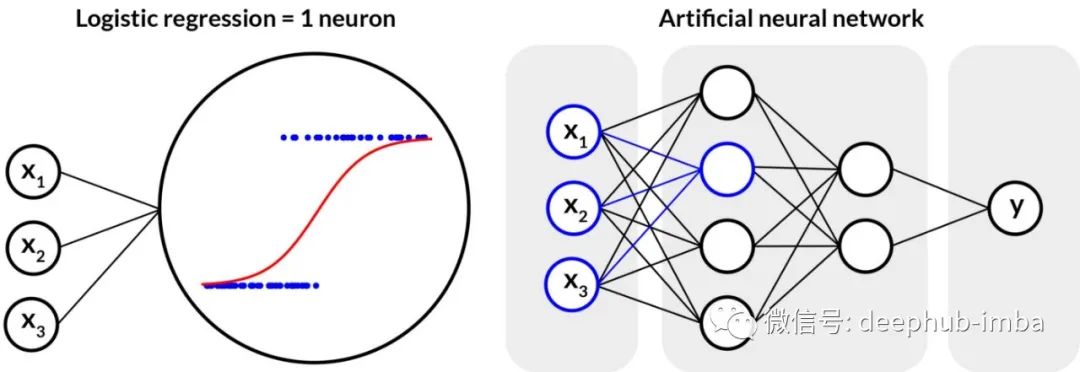
现在,逻辑回归类似于一个人工神经元,连接几个神经元会生成前馈神经网络。不同的特征排列和网络架构最终导致了卷积神经网络、循环神经网络和其他深度学习模型。
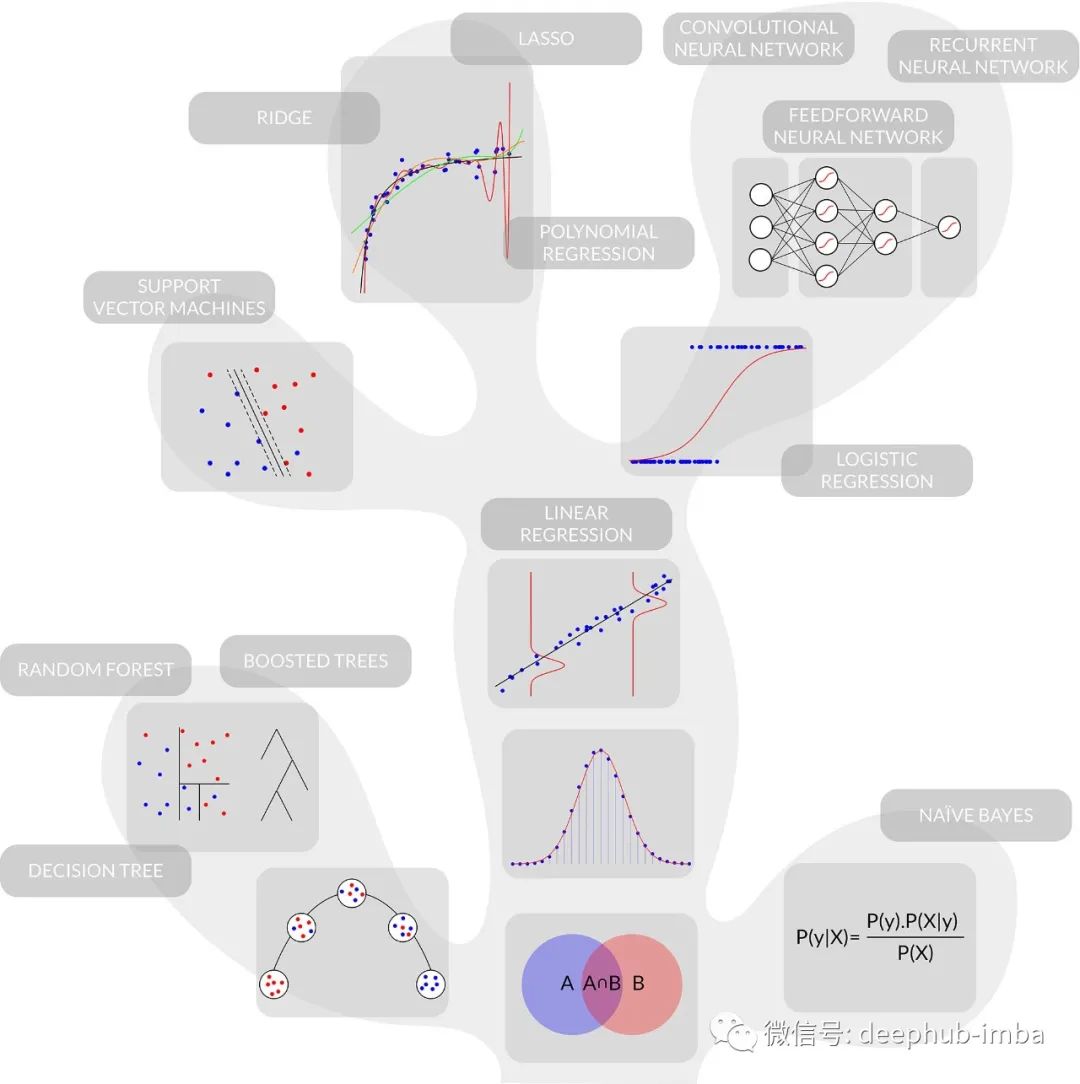
监督学习的进化树
现在已经描述了所有链接关系,让我们在一张最终图表中回顾所有内容。就像生命的系统发育树一样,我们现在可以清楚地看到监督机器学习模型的嵌套。它帮助我们理解不同技术之间的联系,但最重要的是,它为我们提供了一些指导,即在探索偏差/方差权衡时要测试的模型序列。
引用
[1] G.L. McDowell, ‘Cracking the Coding Interview’ (2015), 6th ed., CareerCup, 687 pp.
[2] K.P. Murphy, ‘Machine Learning a Probabilistic Perspective’ (2012), The MIT Press, 1104 pp.
[3] F. Provost & T. Fawcett, ‘Data Science for Business’ (2013), O’Reilly Media, 414 pp.
作者:Arnaud M
喜欢就关注一下吧:
点个 在看 你最好看!********** **********