T-SNE可视化高维数据，亮瞎审稿人

文章目录

t-Distributed Stochastic Neighbor Embedding (t-分布随机邻域嵌入, 简称 t-SNE) 是一种降维技术，特别适用于
高维数据集的可视化

经典案例-MNIST手写数字降维可视化

MNIST 原始数据大小： 60000 * 784，每个数据 784 维
2D-t-SNE后为: 60000 x 2
3D-t-SNE后为: 60000 x 3

可见，把 784 维数据（图像大小 28x28，拉直后为784，对 MNIST 不了解请百度）降成 2 维或 3 维是很大程度上的压缩。降维后的结果如图所示。

2D-t-SNE

3D-t-SNE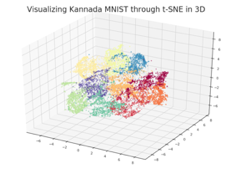

上边是2D-t-SNE，数字0-9一共是10个类，每个类分别是不同的颜色，通过二维图像，我们很容易看到每个类别的分布差异性。

论文中使用 t-SNE 案例

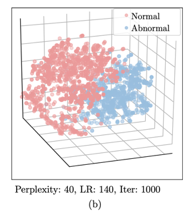
Paper: GANomaly: Semi-Supervised Anomaly Detection via Adversarial Training
把正常数据和异常数据分开用二维展示，可以明显看出两个类别之间的分布是有界限的。

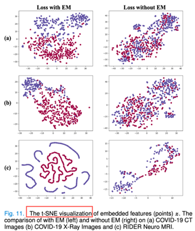
Paper: MAMA Net: Multi-scale Attention Memory Autoencoder Network for Anomaly Detection
使用 t-SNE 可视化模型的潜在空间（比如 U-NET 模型的瓶颈层），以比较使用EM和不使用 EM loss 对潜在空间的影响。

Paper: Unsupervised Detection of Lesions in Brain MRI using constrain-ed adversarial auto-encoders
使用 t-SNE 可视化健康图像和异常图像之间的分布差异性，通过图像可以看出，二者的分布差异较小。

从上面这些例子可以直观看出 t-SNE 在可视化方面用的非常多。在做分类任务之前，我们也可以用它看看不同类别之间有没有明显的分界线。如果分界线明显，可以说明分类任务比较简单。反之则说明类别之间不容易区分，如果我们的分类结果不是很好，可以用此图说明任务的难度。如果分类结果很好，也可以更加展示算法的优势。

当然，这只是例举一个用处，它的作用不止这些。

t-SNE 实战

它的作用了解了，看看怎么用代码实现它。经过多次实践发现，虽然实现他的方法很多，但是最好用最方便的还是使用

sklearn.manifold.TSNE

接下来讲解2个使用该方法的案例

MNIST 可视化教程

kaggle MNIST 可视化教程 上面讲的很详细，还对比 PCA 和 t-SNE 的区别

MRI 脑肿瘤三维数据可视化

实验背景与目的： brats 是三维脑 MRI 肿瘤数据，大小= 240x240x150, 把每个数据中的肿瘤层面看成是异常层，不含肿瘤的层面看成是正常层。使用 t-SNE 可视化，以观察正常层和异常层在分布上是否有差异。

这里的层指的是 axial-slice, 即横断面。一个三维数据有150层，每层的大小都等于240x240

• 1.导入包

import numpy as np
import matplotlib.pyplot as plt
from sklearn import manifold
from glob import glob
import nibabel as nib

• 2.加载数据 我的数据是三维的，格式为 .nii.gz

# load data
brats =sorted(glob('BraTs/*.gz'))
brats_gt =sorted(glob('BraTsseg/*.gz'))

brats_tra =[]
brats_label =[]for i, j inzip(brats, brats_gt):
    brats_np = nib.load(i).get_fdata()
    brats_gt_np = nib.load(j).get_fdata()assert brats_gt_np.shape == brats_np.shape

    z = brats_np.shape[-1]for zi inrange(z):
        brats_tra.append(brats_np[..., zi].flatten())# 横断层拉直，维度=240x240=57600if brats_gt_np[..., zi].any():
            brats_label.append(1)else:
            brats_label.append(0)
            
brats_array = np.array(brats_tra, dtype='uint8')# [6200, 57600]
brats_label_array = np.array(brats_label, dtype='uint8')# [6200]

brats_array 大小为[6200, 57600]， 表示一共有6200层，每层的数据维度是57600，对它进行降维到[6200, 2]

• 3.可视化-使用sklearn-TSNE

tsne = manifold.TSNE(n_components=2, init='pca', random_state=42).fit_transform(brats_array)

tsne shape [6200, 2]， 由于数据维度非常大，还要迭代1000次，因此非常慢。

参数介绍

• n_components（默认值：2）：嵌入空间的维度，需要降到几维写几维。
• init: 初始化方法，多采用 PCA 初始化
• perplexity（默认值：30）：perplexity 与其他流形学习算法中使用的最近邻的数量有关。考虑选择 5 到 50 之间的值。
• n_iter（默认值：1000）：优化的最大迭代次数。应至少为 250。
• random_state： 随机种子
• 还有其他参数可以调整。有关详细信息，请参阅文档

1. t-SNE 归一化

# tsne 归一化， 这一步可做可不做
x_min, x_max = tsne.min(0), tsne.max(0)
tsne_norm =(tsne - x_min)/(x_max - x_min)

1. 根据label，把正常层和异常层分开

normal_idxs =(brats_label_array ==0)
abnorm_idxs =(brats_label_array ==1)
tsne_normal = tsne_norm[normal_idxs]
tsne_abnormal = tsne_norm[abnorm_idxs]

1. 使用matplotlib画出t-SNE

plt.figure(figsize=(8,8))
plt.scatter(tsne_normal[:,0], tsne_normal[:,1],1, color='red', label='Healthy slices')# tsne_normal[i, 0]为横坐标，X_norm[i, 1]为纵坐标，1为散点图的面积， color给每个类别设定颜色
plt.scatter(tsne_abnormal[:,0], tsne_abnormal[:,1],1, color='green', label='Anomalous slices')
plt.legend(loc='upper left')
plt.show()

结果展示：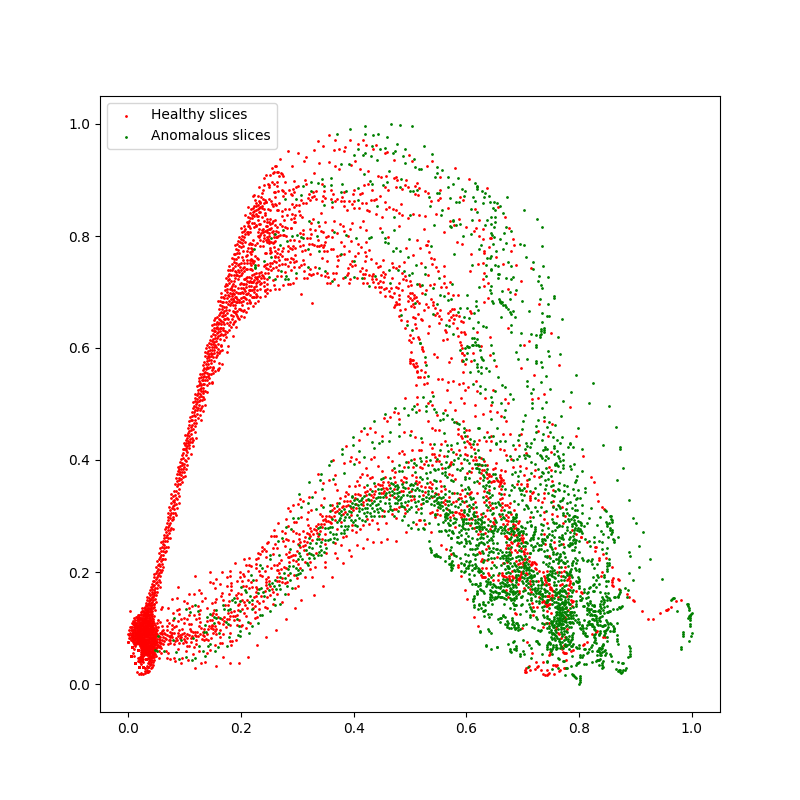

由于进行了归一化，横纵坐标值都在[0,1] 从这个图可以看出，正常层分布在左边，异常在右边，当然也有很多分界不清的区域。

总结： 使用

sklearn.manifold.TSNE

很简单，就一句话搞定了，其余的代码都是为了创建需要降维的数组，以及使用 matplotlib进行展示，真正核心代码就一行。

想了解更多理论知识，请阅读以下链接
TSNE理论知识

文章持续更新，可以关注微信公众号【医学图像人工智能实战营】获取最新动态，一个关注于医学图像处理领域前沿科技的公众号。坚持已实践为主，手把手带你做项目，打比赛，写论文。凡原创文章皆提供理论讲解，实验代码，实验数据。只有实践才能成长的更快，关注我们，一起学习进步~

我是Tina, 我们下篇博客见~

白天工作晚上写文，呕心沥血

觉得写的不错的话最后，求点赞，评论，收藏。或者一键三连