本文主要基于Zeng Bo老师2013年发表于《Operations Research Letters》上的文章《Solving two-stage robust optimization problems using a column-and-constraint generation method》和原文电子版全文。讲解了Zeng提出的 行列生成(column-and constraint generation, C&CG) 算法的思路,以及与传统的 Benders分解切平面法(Benders-style cutting plane methods) 的区别,辅以一个 原文中的 选址-运输问题 的主问题、子问题及其详细迭代和计算讲解,力求能让零基础的同学看懂其中的思路。
- 两阶段鲁棒优化与Benders对偶切平面法
本文讨论的一阶段与二阶段的问题均为线性规划问题,且不确定集为有限离散集(finite discrete set)或多面体集(polyhedron)。
令y为一阶段决策变量,x为二阶段决策变量。不确定集μ为离散集或多面体集,则二阶段鲁棒优化的一般形式(加粗的字母表示向量形式)一阶段问题为:
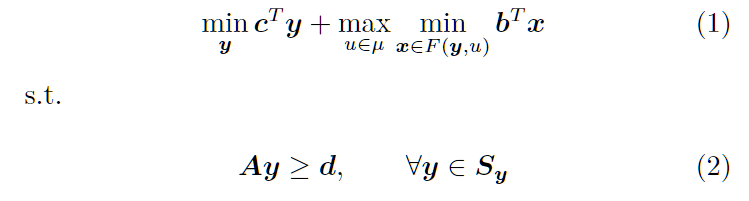
其中,F(x, u)为二阶段问题,如下:
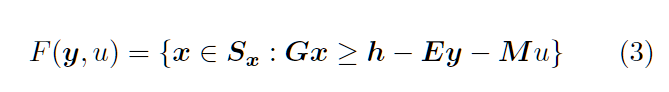
即一阶段问题中不考虑不确定性,做出决策。之后将一阶段的变量y作为常数传入二阶段问题进行求解。这只是建模的思路,想要得到最优解还需要对模型做一些变换及用到算法。
此时二阶段问题为max-min问题,我们根据对偶理论将内层的min问题做一次变换,令π为对偶变量,则转换后的二阶段问题如下,这个问题也是Bender对偶方法的子问题。
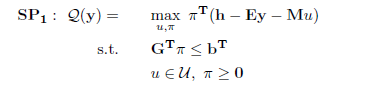
此时的二阶段问题为max问题,但注意 不确定参数u 与 对偶变量π 均为决策变量,目标函数中存在二次项,该问题为双线性(Bilinear)问题,该问题通常为NP-Hard问题。双线性问题的求解可以通过近似方法,也可以利用不确定集的特性将其等价为混合整数规划(Mixed Integer Linear Problem, MILP)问题进行紧缺求解。这转换过程依赖于一个重要的性质:如果U是多面体集,则U和π合二为一的最优解总是在其各自的可行集中取极值点,本文后续的实例中也会用到类似的转化方法。
我们在此处直接将二阶段问题看作可以求解,则Benders对偶切平面算法的流程如下:
Benders-dual Cutting Plane Algorithm
设定目标值上界UB=+∞, 下界LB=-∞,当前迭代次数k=0。
求解以下主问题(Master Problem, MP):
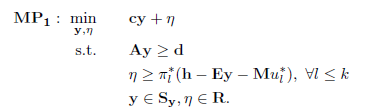
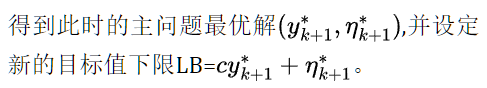
- 求解以下子问题(SubProblem,SP):
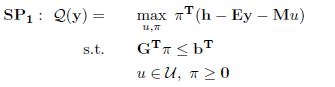

- 如果UB-LB≤ε,其中ε为预先设定好的可以接受的偏差,则返回当前的目标值和最优解y,并退出循环。
否则设定k=k+1,将以下约束添加到主问题MP1中:
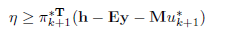
并返回第2步。
- 行列生成(Colume-and-Constraint generation algorithm, C&CG)
为了使得算法便于理解,我们首先考虑当不确定集μ为有限离散集合时的情况,即μ={u1, u2, ..., ur}, {x1, x2, ..., xr}为每种情况下对应的二阶段决策变量。考虑到每种情况下的不确定性,则第一节中的两阶段鲁棒优化可表示如下:
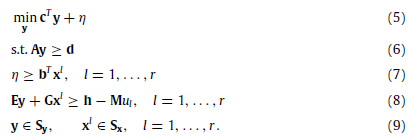
在这种情况下,求解两阶段鲁棒优化可以看作求解一个大规模的混合整数规划(MILP)问题。当不确定集规模很大或者为多面体集时,通过上述这种考虑不确定集μ中所有可能的场景来求解并不现实。但是基于(7)(8)中的约束,我们可以根据不确定集μ上的一个子集来为上述问题提供一个有效的松弛解,以及一个对应的目标值下界。因此,通过逐渐为原问题中添加特定场景来拓展问题,可以逐渐得到预期更强的下界。
基于以上的思想,提出了行列生成算法,通过识别到不确定集中重要的场景来拓展主问题的不确定集,即动态生成相应的决策量和约束(7)(8)。
与Benders分解类似,行列生成算法也应用了 主-子问题 的框架,子问题如下:
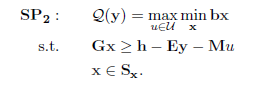
行列生成具体的算法流程如下:
Column-and-constraint generation (C&CG) algorithm
设定下界LB=-∞, 上界UB=+∞, 迭代次数k=0, 变量集O=∅,为空集。
求解以下主问题(MP):
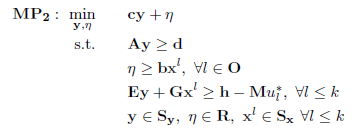
。
- 求解以下子问题(SP):
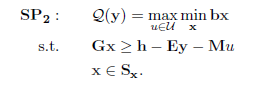
如果UB-LB≤ε,其中ε为预先设定好的可以接受的偏差,则返回当前的目标值和最优解y,并退出循环。
否则:
(a) 若子问题可行,即
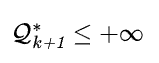
,则在主问题中添加下列约束:
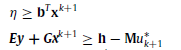
其中u*为子问题的最优解,也即找到的最坏的场景。更新k=k+1, O =O∪{k+1},然后返回第2步进行迭代;
(b) 若子问题不可行,即
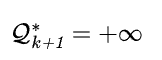
,则在主问题添加下列约束:
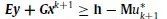
其中u*为子问题的最优解,也即找到使得
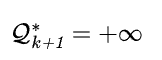
的场景。更新k=k+1, O =O∪{k+1},然后返回第2步进行迭代;
注意上述4(a)中添加的约束为最优切平面,4(b)中添加的约束为可行切平面。
实例:鲁棒选址-运输问题
参数定义、取值 及 确定性模型
考虑以下选址运输问题,商品首先储存于m个备选的仓库中,然后被送到n个客户。参数和决策变量定义如下:
变量定义决
策
变
量yi是否在i地建设仓库,yi∈{1, 0}, i∈1,…,mzii仓库储存多少商品,zi∈R+, i∈1,…,mxij从i仓库到j客户运送多少商品,xij∈R+, i∈1,…,m,j∈1,…n参
数fi建设仓库i的固定成本ai仓库i存储商品的单位成本cij从i仓库到j客户运送单位商品的成本ki仓库i的最大容量dj客户j的需求
则该问题的确定性模型如下:
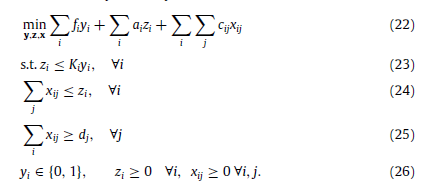
目标函数及约束的定义可以参照原文。确定性模型假设所有顾客的需求都是已知数di,但在现实中顾客需求是不确定的,顾客需求的不确定集表示如下:
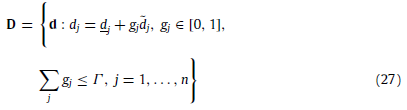

Zeng 在文章中给出了一组用于求解的m,n均等于3的参数取值如下:
fi[400, 414, 326]ai[18, 25, 20]cij[22, 33, 24],
[33, 23, 30],
[20, 25, 27]ki[800, 800, 800]dj[206, 274, 220]dj~[40, 40, 40]
不考虑需求的偏差,确定性模型相当于求解以下线性规划:
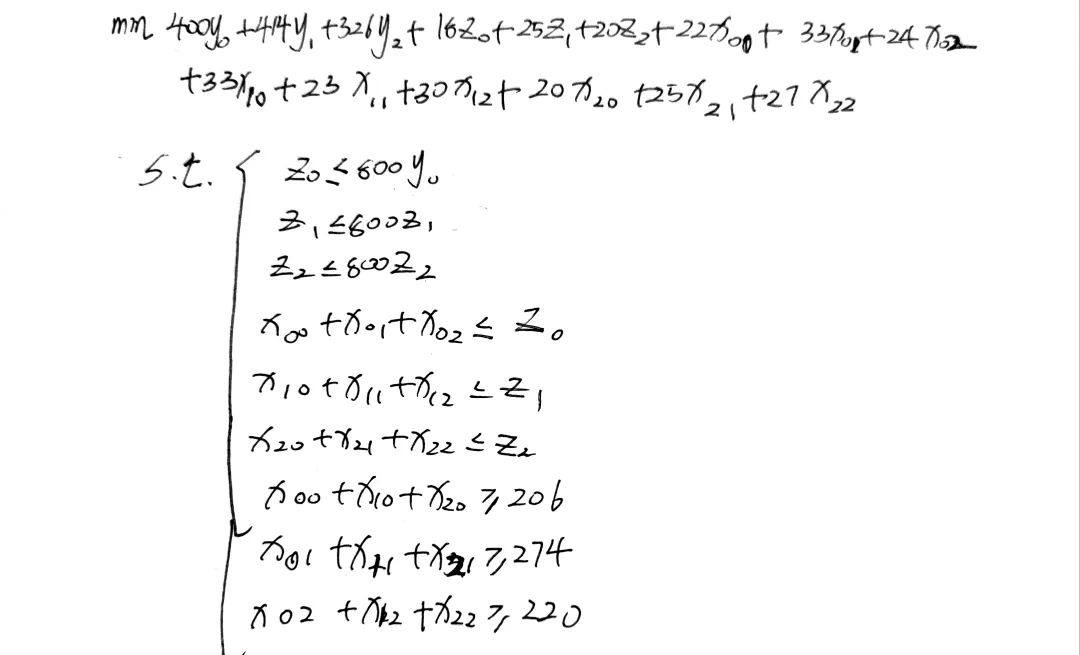
(上面的第2,3条约束有笔误,右侧应该是y1和y2)
使用求解器直接求解,得目标值为30536,y=[1, 0, 1] ,z=[220, 0, 480],
x=[[0, 0, 220], [0, 0, 0], [206, 274, 0]]。
- 两阶段鲁棒模型及转化
在两阶段鲁棒模型中,我们在一阶段未了解到准确的需求,此时做出建设仓库和存储商品的决策;在二阶段了解到顾客需求后,做出运输的决策。第一阶段模型如下:
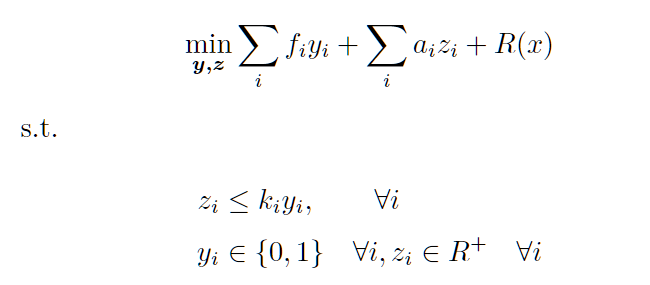
其中,R(x)为二阶段模型,定义如下:
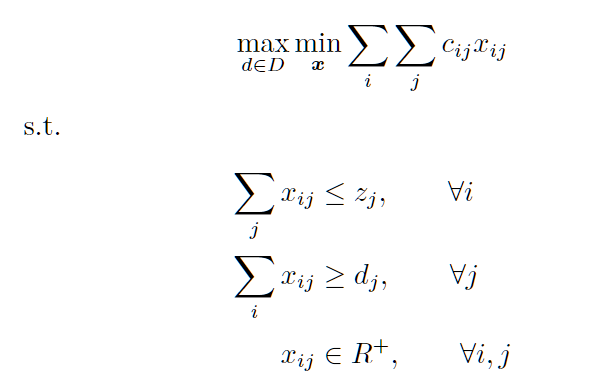
其中不确定集D与d的定义为:
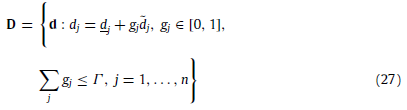
注意此时二阶段问题为max-min问题,不可以使用商业求解器进行求解。所以对二阶段模型进行一对偶,将内层的min问题变为max问题,将二阶段问题变为max问题。令π、λ分别为两条约束产生的对偶变量,二阶段问题如下:
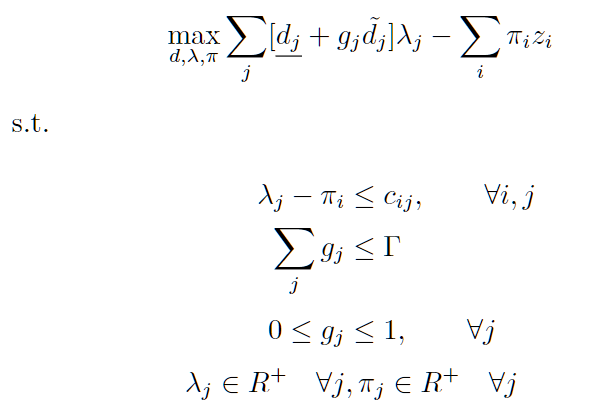
此时g_j也为决策变量,所以目标函数中存在双线性项g_j*λ_j, 因为不确定集D是一个多面体集,且Γ为整数,所以此时g_j∈{0, 1}。引入新变量w_j=λ_j * g_j,将模型转换为混合整数规划MILP模型。M'表示一个很大的数,此时MILP模型如下:
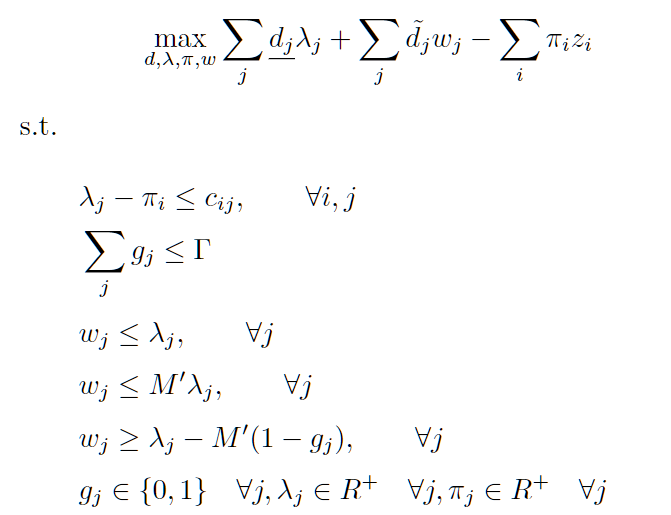
二阶段的MILP模型也同时为Benders分解及C&CG算法的子问题。接下来,我们从实例的角度入手对两种算法分别进行迭代。
- Benders 分解
Benders分解的主问题为鲁棒优化的一阶段问题,MP如下:
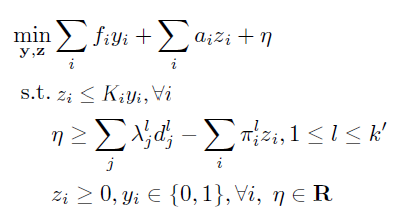
子问题则为转化后的鲁棒优化二阶段问题,SP如下:
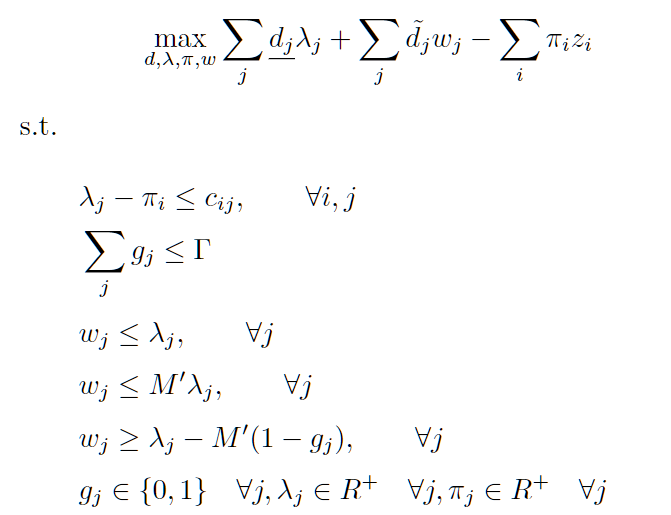
此时开始求解问题,将不确定预算Γ设定为2,M‘设定为1e10,可接受的ε=0.001。根据Benders分解的算法流程,首先设定LB=-∞, UB=+∞, k=0。
k=0时,LB=0,UB=7800000000000
首先对主问题进行求解,此时d不考虑不确定性,即d=[206, 274, 220],相当于求解以下线性规划:
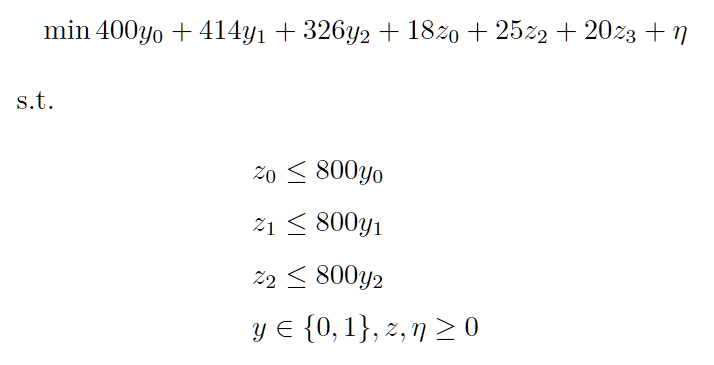
因为此时对偶变量λ和π都无定义,所以η无约束。解上述问题得到此时目标值为0,y=[0, 0, 0], z=[0, 0, 0], η=0。所以更新新的下界即为目标值LB=fy+az+η=0+0=0。
将y和z的值代入子问题中进行求解,相当于求解以下线性规划:

解之得此时目标值为7800000000000,所以此时新的上界LB=0+7800000000000=7800000000000。此时最优解g=[0, 1, 1],
λ=[10000000000,10000000000,10000000000],
π=[9999999978,9999999977,9999999980]。上下界未逼近,所以进入下一次迭代。
k=1, LB=14440,UB=35574
将子问题得到的不确定性预算g代入主问题,得到此时d^1=[206, 314, 260]。将新的一组d、λ和π代入主问题中,添加了一条新的约束,此时的主问题如下:

此时根据上一轮迭代中的对偶变量取值,η有一条约束。解上述问题得到此时目标值为14440,y=[1, 0, 0], z=[780, 0, 0], η=0。所以更新新的下界LB=fy+az+η=14440+0=14440。
将y和z的值代入子问题中进行求解,相当于求解以下线性规划:
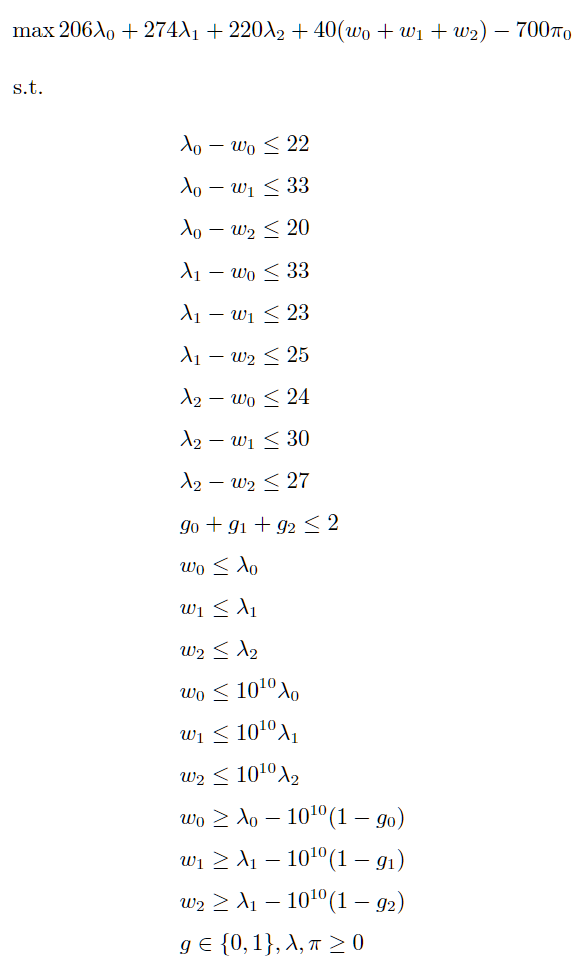
此时因为z的变化,目标函数发生了变化。解之得此时目标值为
21134,所以此时新的上界LB=14440+21134=35574。此时最优解g=[0, 1, 1], λ=[22,33,24],π=[0, 10, 8]。上下界未逼近,所以进入下一次迭代。
k=2, LB=30820,UB=34916
将新的一组d、λ和π代入主问题中,添加了一条新的约束,此时d^2=[206, 314, 260],此时的主问题如下:

此时η有2条约束,注意此问题中d没有发生变化,在实际操作中约束条件需要与上次迭代的d对应。解上述问题得到此时目标值为30820, y=[0, 0, 1], z=[0, 0, 780], η=14894。所以更新新的下界LB=fy+az+η=15926+15534=30820。
将y和z值代入子问题,同样只改变目标函数不改变约束。解之得此时目标值为18990,所以此时新的上界LB=15926+18990=34916。此时最优解g=[0, 1, 1], λ=[20,25,27],π=[3, 2, 0]。上下界未逼近,所以进入下一次迭代。
k=3, LB=33454.182,UB=34016.001
将新的一组d、λ和π代入主问题中,添加了一条新的约束,此时d^3=[206, 314, 260],此时的主问题如下:

此时η有3条约束。解上述问题得到此时目标值为33454.182, y=[1, 0, 1], z=[372.364, 0, 407.636], η=17892.909。所以更新新的下界LB=fy+az+η=15581.273+17892.909=33454.182。
将y和z值代入子问题。解之得此时目标值为18434.728,所以此时新的上界LB=15926+18990=34016.001。此时最优解g=[0, 1, 1], λ=[22,27,24],π=[0, 4, 2]。上下界未逼近,所以进入下一次迭代。
k=4, LB=34016,UB=34016
将新的一组d、λ和π代入主问题中,添加了一条新的约束,d^4=[206, 314, 260],此时的主问题如下:

此时η有4条约束。解上述问题得到此时目标值为34016, y=[1, 0, 1], z=[260, 0, 520], η=18210。所以更新新的下界LB=fy+az+η=15806+18210=34016。
将y和z值代入子问题。解之得此时目标值为18210,所以此时新的上界LB=15806+18210=34016。此时最优解g=[0, 1, 1], λ=[20,25,24],π=[0, 2, 0]。
上下界收敛,所以退出迭代,此时的最优函数值为34016。我们可以观察到在Benders分解算法中,子问题的对偶变量都将传入主问题中,生成新的约束进而进行迭代求解。此问题因为规模较小,所以每次迭代子问题中的不确定参数g都基本相同,在大规模问题中不确定参数g可能会有很大的波动,进而使得收敛变慢。
- Column-and-constraint generation (C&CG)
C&CG的主问题为松弛后的确定性模型,MP如下,此处16为zi≤ki*yi):
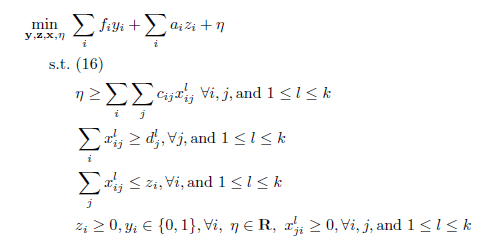
子问题与Benders分解相同,为转化后的鲁棒优化二阶段问题,SP如下:
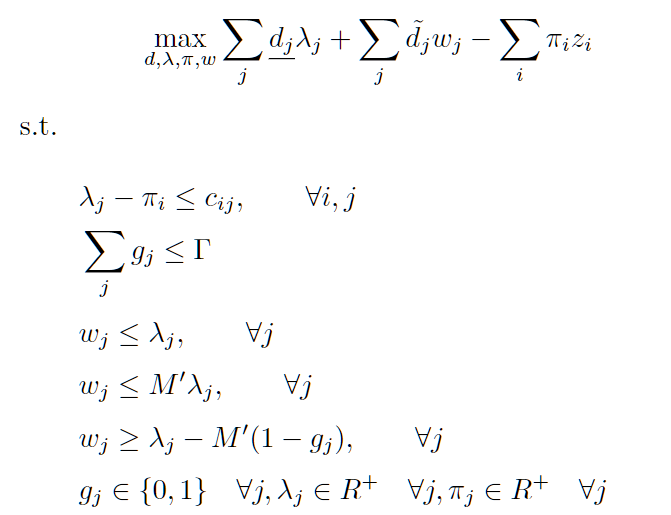
此时开始求解问题,将不确定预算Γ设定为2。根据C&CG算法流程,首先设定LB=-∞, UB=+∞, k=0, 变量集O=∅。
k=0时,LB=0,UB=7800000000000
首先对主问题进行求解,相当于求解以下线性规划:
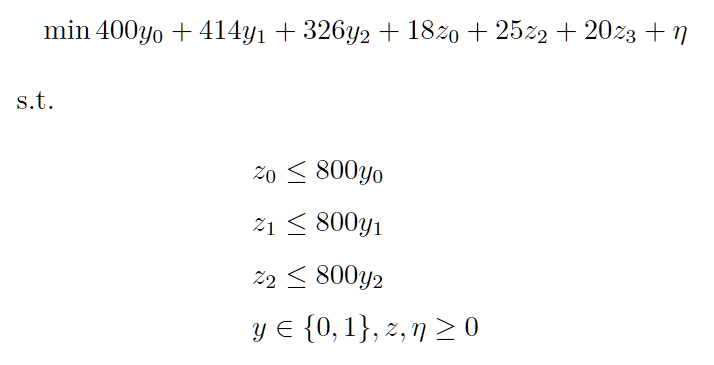
解上述问题得到此时目标值为0,y=[0, 0, 0], z=[0, 0, 0],η=0。所以更新新的下界即为目标值LB=fy+az+η=0+0=0。
将y和z的值代入子问题中进行求解,相当于求解以下线性规划:

解之得此时目标值为7800000000000,所以此时新的上界LB=0+7800000000000=7800000000000。此时最优解g=[0, 1, 1]。上下界未逼近,进入下一次迭代。
k=1, LB=34016,UB=34016
将子问题得到的不确定性预算g代入主问题,得到此时d^1=[206, 314, 260]。生成一组新的变量x^1,主问题相当于求解以下问题:
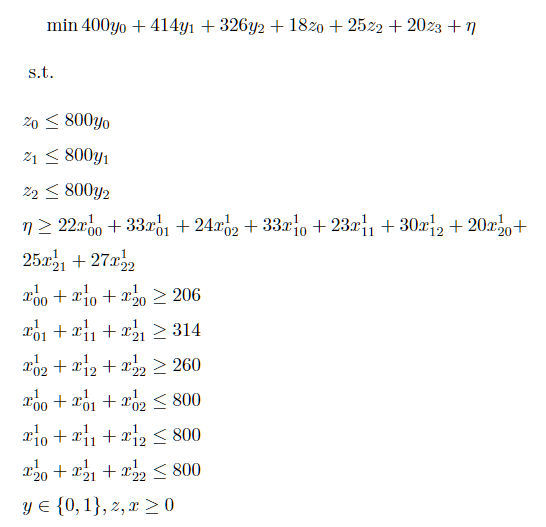
解之得目标值为30146。η=18210,此时新的下界LB=34016,y=[1,0,1],z=[260, 0, 520]。可以看到已经与Benders分解的第四次主问题迭代结果相同。由于两种方法子问题完全相同,可以得到此时的UB=34016。UB-LB=0目标问题已经收敛.
- 总结
综上讨论我们可以看出Benders分解与C&CG算法的不同:Benders分解求解的主问题为鲁棒优化问题的一阶段,而子问题传回主问题的信息包括鲁棒优化二阶段的所有对偶变量的取值。主问题中只会不断生成约束条件,即切平面(Cutting-plane)或者叫行生成。
C&CG算法求解的主问题为部分场景下的确定性模型,子问题传回主问题的信息只包括当前一阶段决策下情况最坏的场景信息,在上述问题中即不确定性参数g。主问题中会根据此时生成的场景,不断生成约束条件和新的决策变脸。这就是C&CG的重要思想,子问题为寻找当前情况下最坏的场景,进而在主问题中生成变量和约束,进行迭代求解。
- 参考文献Zeng, B., & Zhao, L. (2013). Solving two-stage robust optimization problems using a column-and-constraint generation method. Operations Research Letters, 41(5), 457-461.
版权归原作者 张舒政 所有, 如有侵权,请联系我们删除。