[机器学习面试] Day3： 什么是组合特征？如何处理高维组合特征？

[机器学习面试] Day1 : 数据特征归一化以归一化原因

[机器学习面试] Day2 : 数据预处理：序号编码、独热编码、二进制编码

**编辑不易，留个关注吧！一起搞定机器学习面试！！ **

** 什么是组合特征？如何处理高维组合特征？难度：★★☆☆☆**

分析与解答：

为了提高复杂关系的拟合能力，在特征工程中经常会把一阶离散特征两两组合，构成高阶组合特征。以广告点击预估问题为例，原始数据有语言和类型两种离散特征。表1.2是语言和类型对点击的影响。为了提高拟合能力，语言和类型可以组成二阶特征，表1.3是语言和类型的组合特征对点击的影响。

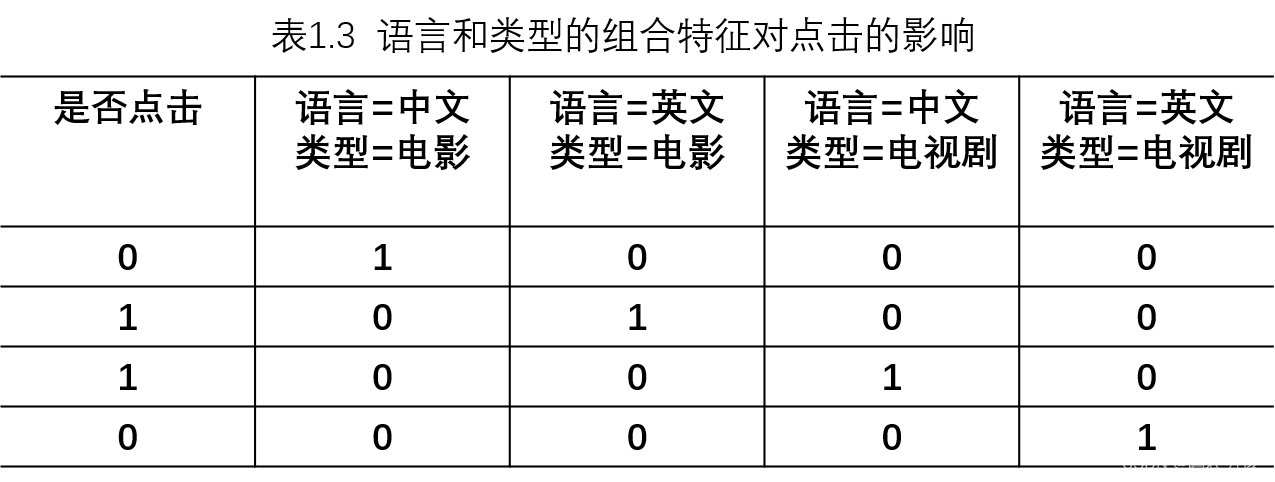
以逻辑回归为例，假设数据的特征向量为，则有

其中**<Xi, Xj>**表示 **Xi **和 **Xj 的组合特征，Wij 的维度等于，|Xi| **和 **|Xj| **分别代表第i个特征和第j个特征不同取值的个数。在表格1.3的广告点击预测问题中，w的维度是2x2=4（语言取值为中文或英文两种、类型的取值为电影或电视剧两种）。这种特征组合看起来是没有任何问题的，但当引入ID类型的特征时，问题就出现了。以推荐问题为例，表格1.4是用户ID和物品ID对点击的影响，表1.5 是用户ID和物品ID的组合特征对点击的影响。

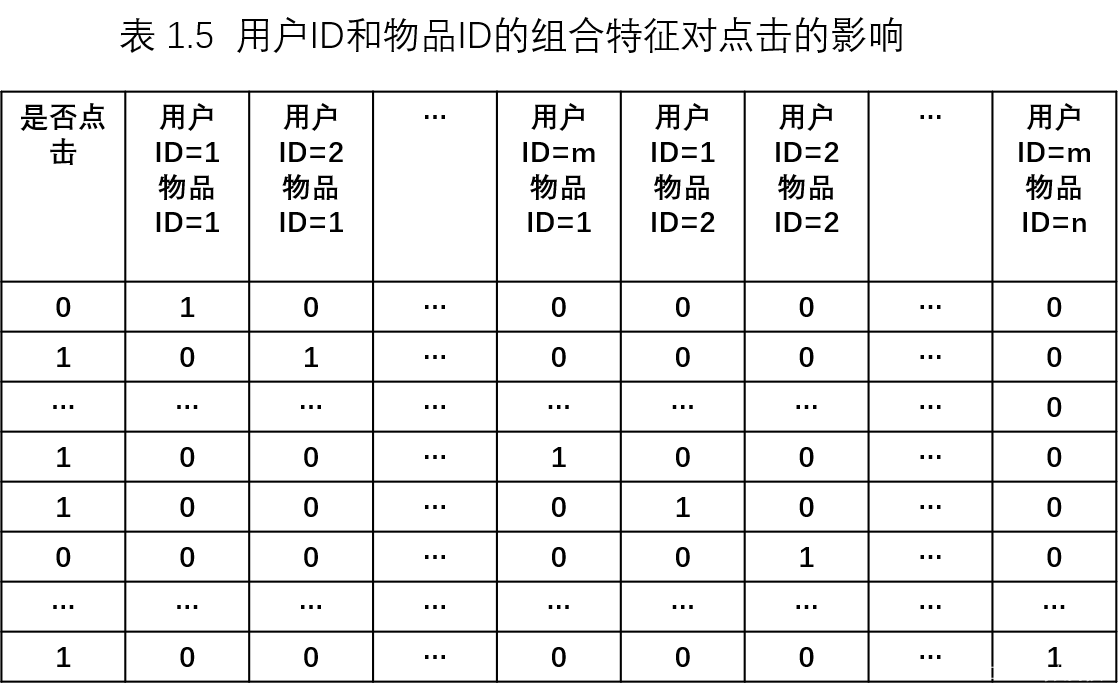
若用户的数量为m、物品的数量为n，那么需要学习的参数的规模为 m x n。在互联网环境下，用户数量和物品数量都可以达到千万量级，几乎无法学习 m x n规模的参数。在这种情况下，一种行之有效的方法是将用户和物品分别用k维的低纬度向量表示（ K<<m，K<<n），

其中, 分别表示Xi和Xj对应的低纬向量。在表1.5的推荐问题中，需要学习的参数的规模变成为 m x k + n x k。熟悉推荐算法的同学很快可以看出来，这其实等价于矩阵分解。所以，这里也提供了另一种理解推荐系统中矩阵分解的思路。