机器学习绪论
机器学习定义
**机器学习(Machine Learning,ML)**并没有统一的定义,周志华老师在《机器学习》(西瓜书)中定义为:计算机系统能够利用经验提高自身的性能。机器学习的统计学定义为:提取重要模式、趋势,并理解数据,即从数据中学习。其实总的来说,机器学习就是从数据中自动的提取知识。机器学习的方法
机器学习的三个要素:模型、策略、方法。 模型:是对问题的一个理解,对问题进行建模,确定问题的假设空间。 策略:从假设空间中选择解决问题最优的方法,确定目标函数。 算法:求解最优模型的具体计算方法,求解出模型的参数。机器学习模型分类

监督学习和无监督学习
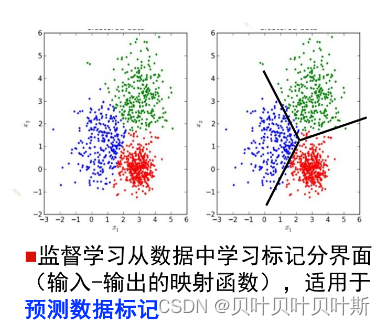
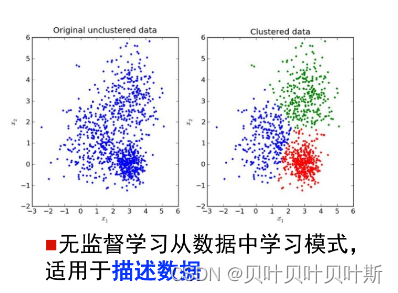
**监督学习(supervised learning)**和**无监督学习(unsupervised learning)**的主要区别在于:监督学习的样本有**标记(label),**而无监督学习的样本没有标记。
此外,无监督学习从数据中学习模式,如数据的分布模式,**适用于描述数据**。监督学习从数据中学习标记数据的分界面,**适用于预测数据标记**。
参数模型和非参数模型
**参数模型(parametric model),**对数据的分布进行观察假设,可以使用一组有限且参数数目固定的模型进行表示。如线性回归、逻辑回归。
有时候数据过于复杂或者没有明显的分布特征,不能事先给出假设来描述数据的分布。此时可以使用**非参数模型(non-parametric model),**即不对数据分布进行假设,数据所有的特征都从原数据中进行学习。如K近邻模型,随机森林。注意,非参数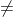无参数,非参数模型中的参数是模型进行自适应得到的,使用这种方式得到的参数的数目不固定,参数的个数随着样本的变化而变化。
参数模型和非参数模型优劣对比
参数模型非参数模型优点数据需求少、训练速度快对数据适应性强,能够拟合的函数形式具有多样化缺点模型复杂度较低,对数据的拟合程度较差数据需求大、易发生过拟合的现象
判别模型和生成模型
判别模型和生成模型建模的对象不同,**生成模型**适合对联合分布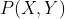进行模型的建立,学习时先得到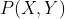,继而得到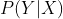,预测时应用最大后验概率法(MAP)得到预测类别。**判别模型**适合对条件分布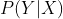进行模型的建立,直接学习得到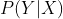,利用MAP得到 类别。
深度学习概述
人工智能、机器学习、深度学习三者关系
人工智能**(Artificial Intelligence, AI)**是一个比较大的概念,总得来说目标是让机器像人类一样有思考的能力,**机器学习**是实现人工智能这一目标的其中一种方法;而在机器学习中使用了深层神经网络的机器学习称为**深度学习(Deep Learning,DL)**。
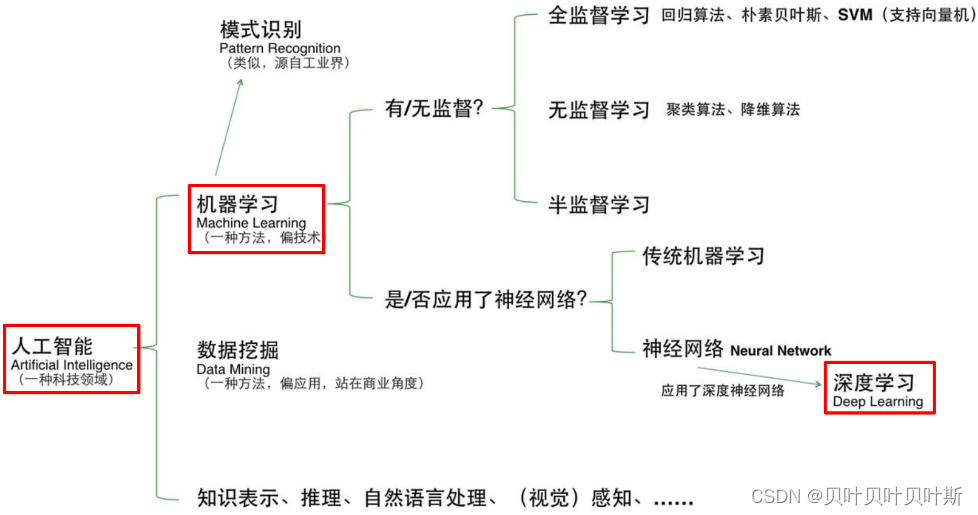
传统机器学习与深度学习的区别
1.在传统的机器学习中,利用特征工程(feature engineering),人为的对数据进行特征提取操作。 2.在深度学习中,利用表示学习(representation learning),使用机器对数据特征自动提取。神经网络的发展历程
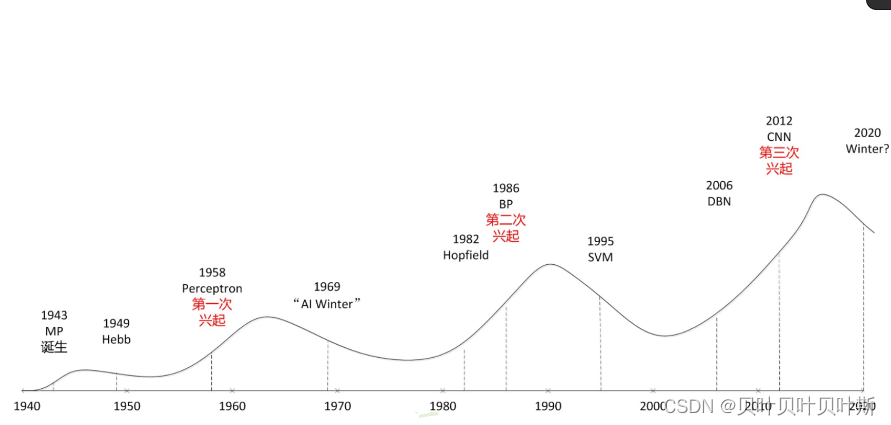
深度学习的缺点
(1).算法不够稳定,容易被“攻击”。例如,在下图中通过往图像中添加噪声干扰,将原来的大象识别为考拉。

(2).模型的复杂程度高,难以纠错和调节。
(3).模型层级符合程度高,参数不透明。在深度学习模型中,第一层的卷积核可以进行可视化操作,而第二层及后面的层没办法通过写出卷积核或者全连接矩阵来理解该层在捕捉什么模式。
(4).端到端训练方式对数据依赖性强,模型增量型差,模型不够灵活。当样本的数据量较小时,无法展现出深度学习强大的拟合能力。
(5).只能专注只管感知类问题,不能解决开放推理性问题。
(6).人类知识无法有效引入进行监督,机器偏见难以避免。例如,美国法院使用COMPAS算法来评估犯罪风险时,对于黑人的危险性评估普遍较高,带有明显的种族歧视色彩。
神经网络
- MP神经元模型
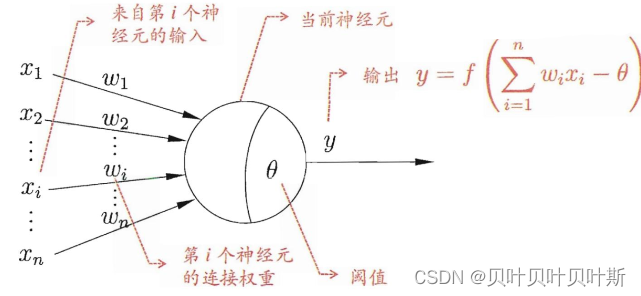
MP神经元模型模拟生物神经元,对于输入部分信号部分进行类加;通过权值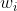的正负来模拟神经元的兴奋或者时抑制;当输入信号的类加超过阈值(bias)时,该神经元就被激活(fire)。
激活函数
(1)sigmoid函数,是最常用的激活函数,但是容易出现梯度缺失的现象。
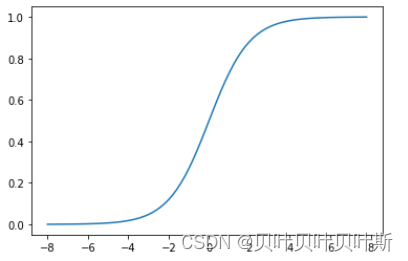
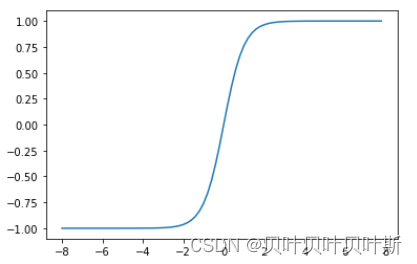
(2)双极S性函数(tanh)

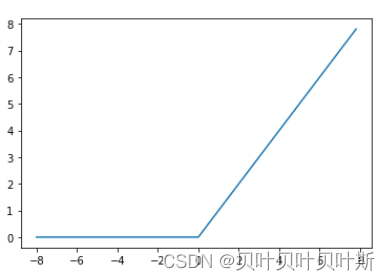
(3) ReLU函数
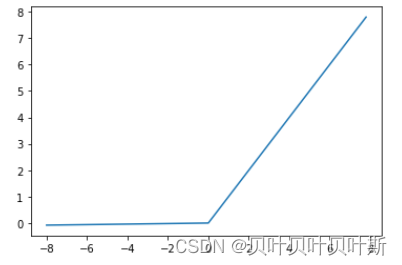
(4) Leak ReLU 在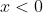的时候添加很小的斜率,使得在自变量小于0时梯度不为0。

单层感知器
单个的神经元无法进行学习,单层感知器(Perceptron)是首个可以学习的人工神经网络。单层感知器由两层神经元组成,输入层接收为外界信号,输出给输出层,输出层是MP神经元。单层感知器能够容易实现逻辑与、或、非运算。

单层感知器模型
多层感知器
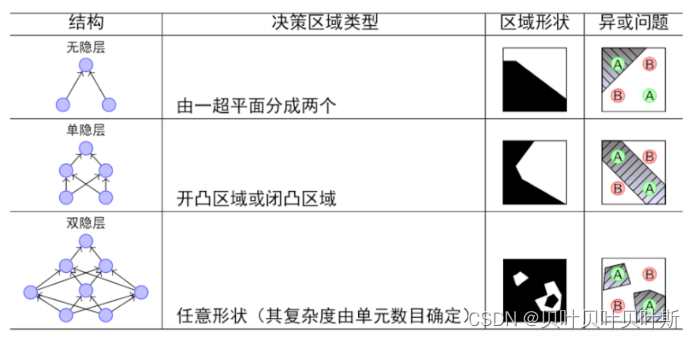
单层感知器不能解决非线性可分的异或问题。类比数字电路,可以通过一组与、或、非门来实现异或。因此就出现了多层感知器。万有逼近定理
如果一个隐层包含足够多的神经元,三层前馈神经网络就能够以任意精度逼近任意预定的连续函数。
误差反向传播
多层感知器的学习能力远大于单层感知器,想要训练多层网络,需要有更强大的学习算法,其中误差反向传播(error BackPropagation,BP)算法是其中最为突出的算法。 误差反向传播算法过程为:正向传播时,输入样本从输入层传入,经隐层逐层处理后,传向输出层。若输出层的实际输出与期望输出不符,则转向误差的反向传播阶段。误差的反向传播是将输出误差以某种形式通过隐层向输入层逐层反传,从而获得各层单元的误差信号,并以此进行神经网络的改进。 这种误差反向传播基于梯度下降策略,在深层的神经网络中有可能会出现梯度消失的现象。逐层预训练
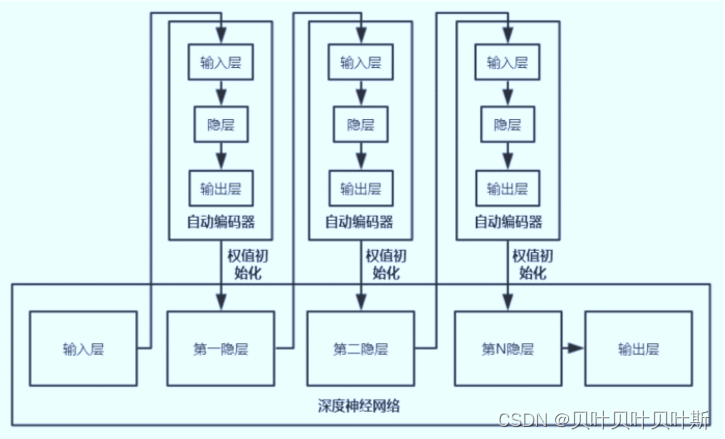
由于深层的网络结构容易出现梯度消失,误差难以传播到浅层的神经元,可以通过与预训练的方法,先从浅层开始向后,每层都进行预训练,从而将浅层神经元的权重调整至误差相对较小,这样即使误差不能传播到较浅的网络层,但是因为经过预训练之后神经元之前的权重调整到相对来说较好的值,因此使用这种方法可以取得较好的一个结果。自编码器
自编码器(autoencoder),假设输出与输入相同,是一种能尽可能复现输入信号的神经网络。通过将输入经过编码以后得到一个密码,再进行解码操作得到输出值,与原输入进行比较计算误差,这样通过调整编码和解码的参数,使得信息重构的误差达到最小。
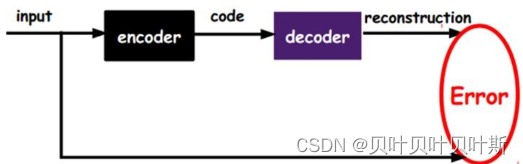
自编码器一般是一个三层或者三层以上的神经网络,其训练目标是使得输出层与输入层的误差最小。中间隐层是代表输入的特征,可以最大程度上代表原输入信号,可以用来信息的降维。
堆叠自编码器(stacked autoencoder,SAE),将多个自编码器的到隐层串联起来,在预训练完成后,进行网络的微调。
Pytorch
- Pytorch基础练习
import torch#需要在anaconda中提前配置torch环境
import numpy as np
#直接定义
#torch.tensor(
# data,
# dtype=None
# device = None 设置设备,cuda/cpu
# requires_grad=False,
# pin_memory=False,是否锁存在内存
# )
x = torch.tensor(456)
print(x)
#创建任意维度数组
arry = np.array([[1,2,3],[4,5,6]])
arr_t = torch.tensor(arry)#此时注意,利用numpy创建的数组和tensor使用的时共享内存,修改任意一个,另一个也会跟着改变
print(arry)
#利用函数创建
arr_1 = torch.ones(3,3)#创建一个3*3的元素都是1的二维张量
arr_2 = torch.rand(5,3)#rand从0-1上进行采样均匀分布
torch.arange(2,10,2)#创建等差为2的1维张量,参数分别为 起始,终止(取不到),公差
torch.linspace(2,10,5)#创建均匀分布的1维张量,参数: 起始,终止(能取到),长度
torch.logspace(1,3,3,2)# 创建对数均分的1维张量,参数:起始,结束,长度,底数(默认10)
#计算是按照 底数的x次方计算
torch.eye(5)#创建单位对角矩阵
torch.normal(1,4,size=(4,2))#创建正态分布 需要给定张量的大小
torch.randn(5)#标准正态分布,均值为0,标准差为1
- 张量的操作
#张量拼接操作
#cat不会增加张量的维度,意思就是本来是几维度的拼接后还是多少维度
arr1 = torch.ones(1,4)
arr2 = torch.zeros(1,4)
print(torch.cat((arr1,arr2),0))#在Y方向
torch.cat((arr1,arr2),1)#在x方向
#张量的切分
a = torch.ones(3,5)
torch.chunk(a,2,0)#切成Y方向的张量
torch.chunk(a,2,1)#切成X方向的张量
print(a[1,:])#取第一行全部元素
#转置
a.t()
#或者
a.transpose(0,1)#0,1代表x方向y方向
#加运算
a = torch.rand(3,5)
print(a)
b = torch.ones_like(a,dtype = float)
torch.add(a,b,alpha = 10)#先是b中的元素*alpha在加上a中对应的元素
c = torch.arange(2,12,2,dtype=float)
print(c)
b[0,:] @ c#一个乘法操作,1*2+1*4+1*6+1*8+1*10 ,注意计算时张量的大小、类型要相同
Sprial Classification
# 引入绘图函数
import wget
url = 'https://raw.githubusercontent.com/Atcold/pytorch-Deep-Learning/master/res/plot_lib.py'
file = wget.download(url)
这里说明一下,!wget命令需要在Linux系统下进行操作,不能直接在windows操作系统上使用。本此是采用pip install wget命令下载wegt资源包,再进行下载,下载默认路径是当前使用的路径。
- 参数设置
# 初始化随机数种子。神经网络的参数都是随机初始化的,
# 不同的初始化参数往往会导致不同的结果,当得到比较好的结果时我们通常希望这个结果是可以复现的,
# 因此,在pytorch中,通过设置随机数种子也可以达到这个目的
seed = 12345
random.seed(seed)
torch.manual_seed(seed)
N = 1000 # 每类样本的数量
D = 2 # 每个样本的特征维度
C = 3 # 样本的类别
H = 100 # 神经网络里隐层单元的数量
- 数据设置并可视化
X = torch.zeros(N * C, D).to(device)
Y = torch.zeros(N * C, dtype=torch.long).to(device)
for c in range(C):
index = 0
t = torch.linspace(0, 1, N) # 在[0,1]间均匀的取10000个数,赋给t
# 下面的代码不用理解太多,总之是根据公式计算出三类样本(可以构成螺旋形)
# torch.randn(N) 是得到 N 个均值为0,方差为 1 的一组随机数,注意要和 rand 区分开
inner_var = torch.linspace( (2*math.pi/C)*c, (2*math.pi/C)*(2+c), N) + torch.randn(N) * 0.2
# 每个样本的(x,y)坐标都保存在 X 里
# Y 里存储的是样本的类别,分别为 [0, 1, 2]
for ix in range(N * c, N * (c + 1)):
X[ix] = t[index] * torch.FloatTensor((math.sin(inner_var[index]), math.cos(inner_var[index])))
Y[ix] = c
index += 1
print("Shapes:")
print("X:", X.size())
print("Y:", Y.size())
#可视化数据
plot_data(X,Y)
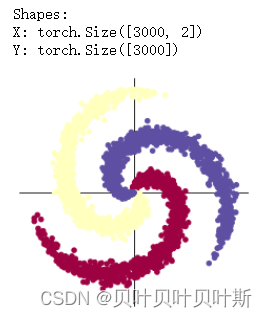
输出结果
- 使用线性模型进行分类
#超参数设置
learning_rate = 1e-3
lambda_l2 = 1e-5
# nn 包用来创建线性模型
# 每一个线性模型都包含权重和偏置
model = nn.Sequential(
nn.Linear(D, H),
nn.Linear(H, C)
)
model.to(device) # 把模型放到GPU上
# nn 包含多种不同的损失函数,这里使用的是交叉熵(cross entropy loss)损失函数
criterion = torch.nn.CrossEntropyLoss()
# 这里使用 optim 包进行随机梯度下降(SGD)优化
optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate, weight_decay=lambda_l2)
# 开始训练
for t in range(1000):
# 把数据输入模型,得到预测结果
y_pred = model(X)
# 计算损失和准确率
loss = criterion(y_pred, Y)
score, predicted = torch.max(y_pred, 1)
acc = (Y == predicted).sum().float() / len(Y)
display.clear_output(wait=True)
# 反向传播前把梯度置 0
optimizer.zero_grad()
# 反向传播优化
loss.backward()
# 更新全部参数
optimizer.step()
#输出结果
print(model)
print('[EPOCH]: %i, [LOSS]: %.6f, [ACCURACY]: %.3f' % (t, loss.item(), acc))
plot_model(X,Y,model)
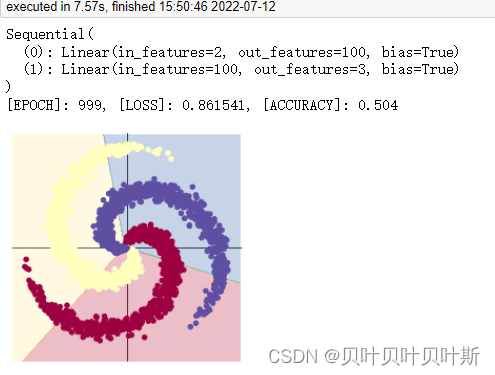
(1) 使用 print(y_pred.shape) 可以看到模型的预测结果,为[3000, 3]的矩阵。每个样本的预测结果为3个,保存在 y_pred 的一行里。值最大的一个,即为预测该样本属于的类别
(2) score, predicted = torch.max(y_pred, 1) 是沿着第二个方向(即X方向)提取最大值。最大的那个值存在 score 中,所在的位置(即第几列的最大)保存在 predicted 中。
(3) 此外,误差每次反向传播前梯度都要清零,是因为梯度在反向传播的过程中是累加的,如果每趟不清零的话,会对下次传播造成影响
(4) 本次模型采用两层网络,第一层输入为2,输出为100;第二层输入为100(第一层的输出),输出为3(数据的3中类别)
- 使用两层神经网络进行分类
#超参数设置
learning_rate = 1e-3
lambda_l2 = 1e-5
# 在两层之间添加 sigmoid激活函数
model = nn.Sequential(
nn.Linear(D, H),
nn.Sigmoid(),
nn.Linear(H, C)
)
model.to(device)
#交叉熵损失,SGD梯度下降优化
criterion = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate, weight_decay=lambda_l2) # built-in L2
# 训练模型,和之前的代码是完全一样的
for t in range(1000):
y_pred = model(X)
loss = criterion(y_pred, Y)
score, predicted = torch.max(y_pred, 1)
acc = ((Y == predicted).sum().float() / len(Y))
display.clear_output(wait=True)
# zero the gradients before running the backward pass.
optimizer.zero_grad()
# Backward pass to compute the gradient
loss.backward()
# Update params
optimizer.step()
#输出模型和结果
print(model)
print("[EPOCH]: %i, [LOSS]: %.6f, [ACCURACY]: %.3f" % (t, loss.item(), acc))
plot_model(X, Y, model)

所使用激活函数模型运行时间损失准确率Sigmoid3.84s0.7485690.523ReLU5.44s0.1705870.953Tanh4.21s0.2969270.850LeakyReLu4.08s0.1648750.955
由上表可以看出,在只有一层隐藏层的情况下Sigmoid函数对于此类分类问题效果较差,但时间运行方面较快,ReLU激活函数以及LeakyReLu激活函数的分类效果突出。
但是,当增加一层隐藏层,使用sigmoid激活函数时,效果也比较好,并且时间上与ReLU作为激活函数相差无几。

版权归原作者 贝叶贝叶贝叶斯 所有, 如有侵权,请联系我们删除。