深度学习实战(四):行人跟踪与摔倒检测报警
转载于集智书童
1. 项目简介
本项目的目的是为了给大家提供跟多的实战思路,抛砖引玉为大家提供一个案例,也希望读者可以根据该方法实现更多的思想与想法,也希望读者可以改进该项目种提到的方法,比如改进其中的行人检测器、跟踪方法、行为识别算法等等。
1.1 相关工作
(1)图卷积网络主要有两种主流方法:
基于光谱的观点(spectral perspective):图卷积中的位置信息被看做是以光谱分析的形式。
基于空间的观点(spatial perspective):卷积核直接被应用在图节点和他们的邻居节点。
作者采用第二种做法,限制每一个滤波只应用到一个节点的一个邻域。
(2)基于骨架的动作识别:
基于手工特征的方法:设计几种手工特征去捕获连接点的运动信息,比如,关节点轨迹的协方差矩阵。
基于深度学习的方法:循环神经网络,端到端进行动作识别。
在这些方法中,许多都强调了人体各部分关节建模的重要性。但是这些部分通 常是使用领域知识显式分配的。作者是第一个将图卷积网络应用在基于骨架的动作识别任务中的。它和以前的方法都不同,可以隐式地通过图卷积网络将位置信息和时序动态信息结合起来。
本项目主要检测识别的行为有7类:Standing, Walking, Sitting, Lying Down, Stand up, Sit down, Fall Down。
2.方法简介
本文涉及的方法与算法包括:YOLO V3 Tiny、Deepsort、ST-GCN方法,其中YOLO V3 Tiny用于行人检测、DeepSort用于跟踪、而ST-GCN则是用于行为检测。
2.1 总体结构
这里由于YOLO与DeepSort大家都已经比较了解,因此这里只简单说明一下ST-GCN 的流程,这里ST-GCN 的方法结构图如下: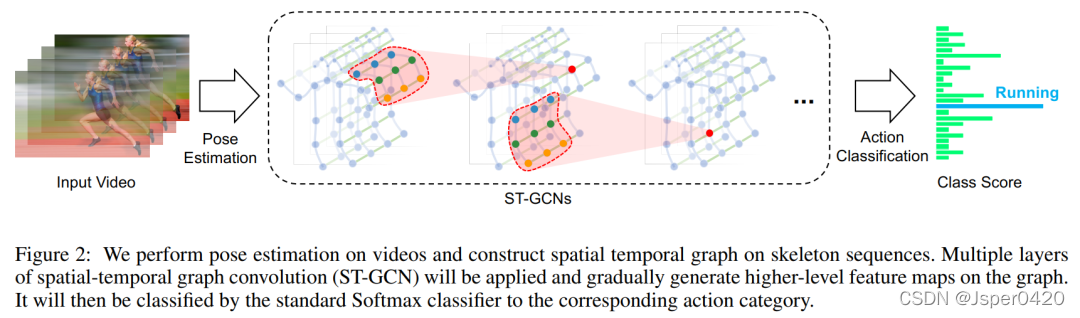
给出一个动作视频的骨架序列信息,首先构造出表示该骨架序列信息的图结构,ST-GCN的输入就是图节点上的关节坐标向量,然后是一系列时空图卷积操作来提取高层的特征,最后用SofMax分类器得到对应的动作分类。整个过程实现了端到端的训练。
2.2 骨架的图结构
设一个有N个节点和T帧的骨架序列的时空图为G=(V,E),其节点集合为V={vti|t=1,…,T,i=1,…,N},第t帧的第i个节点的特征向量F(vti)由该节点的坐标向量和估计置信度组成。
图结构由两个部分组成:
- 根据人体结构,将每一帧的节点连接成边,这些边形成spatial edges ES={vtivtj|(i,j)∈H}。H是一组自然连接的人体关节。
- 将连续两帧中相同的节点连接成边,这些边形成temporal edges EF={vtiv(t+1)i}。

蓝色圆点表示身体关节。人体关节间的体内边缘是根据人体的自然联系来定义的。帧间边缘连接连续帧之间的相同关节。关节坐标用作ST-GCN的输入。
2.3 空间图卷积网络
以常见的图像的二维卷积为例,针对某一位置x的卷积输出可以写成如下形式:
f
out
(
x
)
=
∑
h
=
1
K
∑
w
=
1
K
f
i
n
(
p
(
x
,
h
,
w
)
)
⋅
w
(
h
,
w
)
f_{\text {out }}(\mathbf{x})=\sum_{h=1}^{K} \sum_{w=1}^{K} f_{i n}(\mathbf{p}(\mathbf{x}, h, w)) \cdot \mathbf{w}(h, w)
fout (x)=h=1∑Kw=1∑Kfin(p(x,h,w))⋅w(h,w)
输入通道数为
c
c
c 的特征图fin,卷积核大小
K
∗
K
K * K
K∗K , sampling function采样函数
p
(
x
,
h
,
w
)
=
x
+
p
′
(
h
,
w
)
p(x, h, w)=x+p^{\prime}(h, w)
p(x,h,w)=x+p′(h,w) , weight function通道数为
c
c
c 的权重函数。
2.3.1 Sampling Function
在图像中,采样函数
p
(
h
,
w
)
p(h, w)
p(h,w) 指的是以
x
x
x 像素为中心的周围邻居像素,在图中,邻居像素集合被定义为:
B
(
v
t
i
)
=
{
v
t
j
∣
d
(
v
t
j
,
v
t
i
)
≤
D
}
,
d
(
v
t
j
,
v
t
i
)
B(v_{ti})=\{v_{tj}|d(v_{tj},v_{ti})\leq D\} , d(v t j, v t i)
B(vti)={vtj∣d(vtj,vti)≤D},d(vtj,vti) 指 的是从
v
t
j
v_{tj}
vtj到
v
t
i
v_{ti}
vti的最短距离,因此采样函数可以写成
p
(
v
t
i
,
v
t
j
)
=
v
t
j
p(v_{ti},v_{tj})=v_{tj}
p(vti,vtj)=vtj。
2.3.2 Weight Function
在2D卷积中,邻居像素规则地排列在中心像素周围,因此可以根据空间顺序用规则的卷积核对其进行卷积操作。类比2D卷积,在图中,将 s a m p l i n g ~ f u n c t i o n 得 到 的 邻 居 像 素 划 分 成 不 同 的 子 集 , 每 一 个 子 集 有 一 个 数 字 标 签 , 因 此 有
l
t
i
l_{ti}
lti:
B
(
v
t
i
)
B(v_{ti})
B(vti) → { 0,…,K-1} 到对应的子集标签,权重方程为
w
(
v
t
i
,
v
t
j
)
w(v_{ti},v_{tj})
w(vti,vtj)=
w
′
(
l
t
i
(
v
t
j
)
)
{w'}\left(l_{t i}\left(v_{t j}\right)\right)
w′(lti(vtj))。
2.3.3 空间图卷积
f
out
(
v
t
i
)
=
∑
v
t
j
∈
B
(
v
t
i
)
1
Z
t
i
(
v
t
j
)
f
i
n
(
p
(
v
t
i
,
v
t
j
)
)
⋅
w
(
v
t
i
Z
t
i
(
v
t
j
)
=
∣
{
v
t
k
∣
l
t
i
(
v
t
k
)
=
l
t
i
(
v
t
j
)
}
∣
\begin{aligned} f_{\text {out }}\left(v_{t i}\right)=& \sum_{v_{t j} \in B\left(v_{t i}\right)} \frac{1}{Z_{t i}\left(v_{t j}\right)} f_{i n}\left(\mathbf{p}\left(v_{t i}, v_{t j}\right)\right) \cdot \mathbf{w}\left(v_{t i}\right.\\ & Z_{t i}\left(v_{t j}\right)=\left|\left\{v_{t k} \mid l_{t i}\left(v_{t k}\right)=l_{t i}\left(v_{t j}\right)\right\}\right| \end{aligned}
fout (vti)=vtj∈B(vti)∑Zti(vtj)1fin(p(vti,vtj))⋅w(vtiZti(vtj)=∣{vtk∣lti(vtk)=lti(vtj)}∣
其中,归一化项 等价于对应子集的基。将上述公式带入上式得到:
f
out
(
v
t
i
)
=
∑
v
t
j
∈
B
(
v
t
i
)
1
Z
t
i
(
v
t
j
)
f
i
n
(
v
t
j
)
⋅
w
(
l
t
i
(
v
t
j
)
)
f_{\text {out }}\left(v_{t i}\right)=\sum_{v_{t j} \in B\left(v_{t i}\right)} \frac{1}{Z_{t i}\left(v_{t j}\right)} f_{i n}\left(v_{t j}\right) \cdot \mathbf{w}\left(l_{t i}\left(v_{t j}\right)\right)
fout (vti)=∑vtj∈B(vti)Zti(vtj)1fin(vtj)⋅w(lti(vtj))
2.3.4 时空模型
将空间域的模型扩展到时间域中,得到的Sampling Function为
B
(
v
t
i
)
=
{
v
q
j
∣
d
(
v
t
j
,
v
t
i
)
≤
K
,
∣
q
−
t
∣
≤
⌊
Γ
/
2
⌋
}
B\left(v_{t i}\right)=\left\{v_{q j}\left|d\left(v_{t j}, v_{t i}\right) \leq K,\right| q-t \mid \leq\lfloor\Gamma / 2\rfloor\right\}
B(vti)={vqj∣d(vtj,vti)≤K,∣q−t∣≤⌊Γ/2⌋}
控制时间域的卷积核大小,weight function为
l
S
T
(
v
q
j
)
=
l
t
i
(
v
t
j
)
+
(
q
−
t
+
⌊
Γ
/
2
⌋
)
×
K
l_{S T}\left(v_{q j}\right)=l_{t i}\left(v_{t j}\right)+(q-t+\lfloor\Gamma / 2\rfloor) \times K
lST(vqj)=lti(vtj)+(q−t+⌊Γ/2⌋)×K
2.4 划分子集

(a)输入骨架的示例帧,身体关节用蓝点绘制。D=1的滤波器的接收域用红色虚线圆圈表示。
(b)唯一划分 Uni-labeling:将节点的1邻域划分为一个子集。
(c)基于距离的划分 Distance partitioning:将节点的1邻域划分为两个子集,节点本身子集与邻节点子集。
(d)空间构型划分 Spatial configuration partitioning:将节点的1邻域划分为3个子集,第一个子集连接了空间位置上比根节点更远离整个骨架的邻居节点,第二个子集连接了更靠近中心的邻居节点,第三个子集为根节点本身,分别表示了离心运动、向心运动和静止的运动特征。
2.5 注意力机制
在运动过程中,不同的躯干重要性是不同的。例如腿的动作可能比脖子重要,通过腿部我们甚至能判断出跑步、走路和跳跃,但是脖子的动作中可能并不包含多少有效信息。
因此,ST-GCN 对不同躯干进行了加权(每个 st-gcn 单元都有自己的权重参数用于训练)。
2.6 TCN
GCN 帮助我们学习了到空间中相邻关节的局部特征。在此基础上,我们需要学习时间中关节变化的局部特征。如何为 Graph 叠加时序特征,是图卷积网络面临的问题之一。这方面的研究主要有两个思路:时间卷积(TCN)和序列模型(LSTM)。
ST-GCN 使用的是 TCN,由于形状固定,可以使用传统的卷积层完成时间卷积操作。为了便于理解,可以类比图像的卷积操作。st-gcn 的 feature map 最后三个维度的形状为(C,V,T),与图像 feature map 的形状(C,W,H)相对应。
图像的通道数C对应关节的特征数C。图像的宽W对应关键帧数V。图像的高H对应关节数T。
在图像卷积中,卷积核的大小为『w』×『1』,则每次完成w行像素,1列像素的卷积。『stride』为s,则每次移动s像素,完成1行后进行下1行像素的卷积。
在时间卷积中,卷积核的大小为『temporal_kernel_size』×『1』,则每次完成1个节点,temporal_kernel_size 个关键帧的卷积。『stride』为1,则每次移动1帧,完成1个节点后进行下1个节点的卷积。
3. 训练
训练如下:
输入的数据首先进行batch normalization,然后在经过9个ST-GCN单元,接着是一个global pooling得到每个序列的256维特征向量,最后用SoftMax函数进行分类,得到最后的标签。
每一个ST-GCN采用Resnet的结构,前三层的输出有64个通道,中间三层有128个通道,最后三层有256个通道,在每次经过ST-CGN结构后,以0.5的概率随机将特征dropout,第4和第7个时域卷积层的strides设置为2。用SGD训练,学习率为0.01,每10个epochs学习率下降0.1。
ST-GCN 最末卷积层的响应可视化结果图如下:
项目主函数代码如下:
import os
import cv2
import time
import torch
import argparse
import numpy as np
from Detection.Utils import ResizePadding
from CameraLoader import CamLoader, CamLoader_Q
from DetectorLoader import TinyYOLOv3_onecls
from PoseEstimateLoader import SPPE_FastPose
from fn import draw_single
from Track.Tracker import Detection, Tracker
from ActionsEstLoader import TSSTG
# source = '../Data/test_video/test7.mp4'# source = '../Data/falldata/Home/Videos/video (2).avi' # hard detect
source ='./output/test3.mp4'# source = 2defpreproc(image):"""preprocess function for CameraLoader.
"""
image = resize_fn(image)
image = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)return image
defkpt2bbox(kpt, ex=20):"""Get bbox that hold on all of the keypoints (x,y)
kpt: array of shape `(N, 2)`,
ex: (int) expand bounding box,
"""return np.array((kpt[:,0].min()- ex, kpt[:,1].min()- ex,
kpt[:,0].max()+ ex, kpt[:,1].max()+ ex))if __name__ =='__main__':
par = argparse.ArgumentParser(description='Human Fall Detection Demo.')
par.add_argument('-C','--camera', default=source,# required=True, # default=2,help='Source of camera or video file path.')
par.add_argument('--detection_input_size',type=int, default=384,help='Size of input in detection model in square must be divisible by 32 (int).')
par.add_argument('--pose_input_size',type=str, default='224x160',help='Size of input in pose model must be divisible by 32 (h, w)')
par.add_argument('--pose_backbone',type=str, default='resnet50',help='Backbone model for SPPE FastPose model.')
par.add_argument('--show_detected', default=False, action='store_true',help='Show all bounding box from detection.')
par.add_argument('--show_skeleton', default=True, action='store_true',help='Show skeleton pose.')
par.add_argument('--save_out',type=str, default='./output/output3.mp4',help='Save display to video file.')
par.add_argument('--device',type=str, default='cuda',help='Device to run model on cpu or cuda.')
args = par.parse_args()
device = args.device
# DETECTION MODEL.
inp_dets = args.detection_input_size
detect_model = TinyYOLOv3_onecls(inp_dets, device=device)# POSE MODEL.
inp_pose = args.pose_input_size.split('x')
inp_pose =(int(inp_pose[0]),int(inp_pose[1]))
pose_model = SPPE_FastPose(args.pose_backbone, inp_pose[0], inp_pose[1], device=device)# Tracker.
max_age =30
tracker = Tracker(max_age=max_age, n_init=3)# Actions Estimate.
action_model = TSSTG()
resize_fn = ResizePadding(inp_dets, inp_dets)
cam_source = args.camera
iftype(cam_source)isstrand os.path.isfile(cam_source):# Use loader thread with Q for video file.
cam = CamLoader_Q(cam_source, queue_size=1000, preprocess=preproc).start()else:# Use normal thread loader for webcam.
cam = CamLoader(int(cam_source)if cam_source.isdigit()else cam_source,
preprocess=preproc).start()# frame_size = cam.frame_size# scf = torch.min(inp_size / torch.FloatTensor([frame_size]), 1)[0]
outvid =Falseif args.save_out !='':
outvid =True
codec = cv2.VideoWriter_fourcc(*'mp4v')print((inp_dets *2, inp_dets *2))
writer = cv2.VideoWriter(args.save_out, codec,25,(inp_dets *2, inp_dets *2))
fps_time =0
f =0while cam.grabbed():
f +=1
frame = cam.getitem()
image = frame.copy()# Detect humans bbox in the frame with detector model.
detected = detect_model.detect(frame, need_resize=False, expand_bb=10)# Predict each tracks bbox of current frame from previous frames information with Kalman filter.
tracker.predict()# Merge two source of predicted bbox together.for track in tracker.tracks:
det = torch.tensor([track.to_tlbr().tolist()+[0.5,1.0,0.0]], dtype=torch.float32)
detected = torch.cat([detected, det], dim=0)if detected isnotNoneelse det
detections =[]# List of Detections object for tracking.if detected isnotNone:# detected = non_max_suppression(detected[None, :], 0.45, 0.2)[0]# Predict skeleton pose of each bboxs.
poses = pose_model.predict(frame, detected[:,0:4], detected[:,4])# Create Detections object.
detections =[Detection(kpt2bbox(ps['keypoints'].numpy()),
np.concatenate((ps['keypoints'].numpy(),
ps['kp_score'].numpy()), axis=1),
ps['kp_score'].mean().numpy())for ps in poses]# VISUALIZE.if args.show_detected:for bb in detected[:,0:5]:
frame = cv2.rectangle(frame,(bb[0], bb[1]),(bb[2], bb[3]),(0,0,255),1)# Update tracks by matching each track information of current and previous frame or# create a new track if no matched.
tracker.update(detections)# Predict Actions of each track.for i, track inenumerate(tracker.tracks):ifnot track.is_confirmed():continue
track_id = track.track_id
bbox = track.to_tlbr().astype(int)
center = track.get_center().astype(int)
action ='pending..'
clr =(0,255,0)# Use 30 frames time-steps to prediction.iflen(track.keypoints_list)==30:
pts = np.array(track.keypoints_list, dtype=np.float32)
out = action_model.predict(pts, frame.shape[:2])
action_name = action_model.class_names[out[0].argmax()]
action ='{}: {:.2f}%'.format(action_name, out[0].max()*100)if action_name =='Fall Down':
clr =(255,0,0)elif action_name =='Lying Down':
clr =(255,200,0)# VISUALIZE.if track.time_since_update ==0:if args.show_skeleton:
frame = draw_single(frame, track.keypoints_list[-1])
frame = cv2.rectangle(frame,(bbox[0], bbox[1]),(bbox[2], bbox[3]),(0,255,0),1)
frame = cv2.putText(frame,str(track_id),(center[0], center[1]), cv2.FONT_HERSHEY_COMPLEX,0.4,(255,0,0),2)
frame = cv2.putText(frame, action,(bbox[0]+5, bbox[1]+15), cv2.FONT_HERSHEY_COMPLEX,0.4, clr,1)# Show Frame.
frame = cv2.resize(frame,(0,0), fx=2., fy=2.)
frame = cv2.putText(frame,'%d, FPS: %f'%(f,1.0/(time.time()- fps_time)),(10,20), cv2.FONT_HERSHEY_SIMPLEX,0.5,(0,255,0),1)
frame = frame[:,:,::-1]
fps_time = time.time()if outvid:
writer.write(frame)
cv2.imshow('frame', frame)if cv2.waitKey(1)&0xFF==ord('q'):break# Clear resource.
cam.stop()if outvid:
writer.release()
cv2.destroyAllWindows()




项目论文:https://arxiv.org/abs/1801.07455
项目源码:公主号AiCharm 输入“摔倒检测”****
版权归原作者 AiCharm 所有, 如有侵权,请联系我们删除。