政安晨：【完全零基础】认知人工智能（五）【超级简单】的【机器学习神经网络】 —— 数据训练

回顾

作为这个系列文章的最后一篇，咱们先回顾一下建立神经网络的整体步骤，以实现对机器学习神经网络的整体认知：

在人工智能领域中，机器学习神经网络的数据训练部分是指通过将大量的输入数据输入到神经网络中，利用反向传播算法来调整网络中的参数，从而使得网络能够学习到输入数据的特征和模式。

数据训练部分通常包括以下几个步骤：

1. 数据准备：首先要准备大量的标注数据，这些数据有已知的输入和输出值。输入数据通常是一组向量或矩阵的形式，输出数据可以是分类标签、连续值等。同时，还需要将数据集划分为训练集、验证集和测试集。
2. 初始化参数：神经网络中的参数（权重和偏置）需要进行初始化，可以使用随机数或者其他方法。
3. 前向传播：将输入数据通过网络的每一层传递，并计算输出。每一层的输出都是下一层的输入，直到到达输出层。
4. 计算损失：将网络的输出与真实值进行比较，通过某种损失函数来计算网络输出与真实值之间的差异。
5. 反向传播：根据损失函数的计算结果，通过链式法则计算每个参数对损失函数的梯度。
6. 参数更新：根据计算得到的梯度，使用优化算法（如随机梯度下降）来更新网络中的参数，目的是使损失函数逐渐减小。
7. 重复迭代：以上步骤是一个迭代过程，通过多次迭代来逐步优化网络的参数，使得网络能够更好地拟合输入数据。
8. 模型评估：使用验证集来评估训练后的模型的性能，可以计算准确率、精确率、召回率等指标。
9. 测试模型：最后使用独立的测试集来评估模型的泛化能力，即模型对未见过的数据的预测能力。

数据训练部分的目的是通过大量的数据和反向传播算法来调整网络参数，使得网络能够学习到输入数据的特征和模式，从而实现对未知数据的准确预测或分类。

第一次看到这个系列的小伙伴，可以看一下我这个系列的前面几篇文章：
政安晨：【完全零基础】认知人工智能（一）【超级简单】的【机器学习神经网络】 —— 预测机https://blog.csdn.net/snowdenkeke/article/details/136139504政安晨：【完全零基础】认知人工智能（二）【超级简单】的【机器学习神经网络】—— 底层算法https://blog.csdn.net/snowdenkeke/article/details/136141888政安晨：【完全零基础】认知人工智能（三）【超级简单】的【机器学习神经网络】—— 三层神经网络示例https://blog.csdn.net/snowdenkeke/article/details/136151970政安晨：【完全零基础】认知人工智能（四）【超级简单】的【机器学习神经网络】—— 权重矩阵https://blog.csdn.net/snowdenkeke/article/details/136160424

误差

神经网络的输出是一个极其复杂困难的函数，这个函数具有许多参数影响到其输出的链接权重。

我们可以使用梯度下降法，计算出正确的权重吗？

只要我们选择了合适的误差函数，这是完全可以的。神经网络本身的输出函数不是一个误差函数。但我们知道，由于误差是目标训练值与实际输出值之间的差值，因此我们可以很容易地把输出函数变成误差函数。

咱们再仔细观察一下如下表格（这是3个输出节点的目标值和实际值以及误差函数的候选项）：

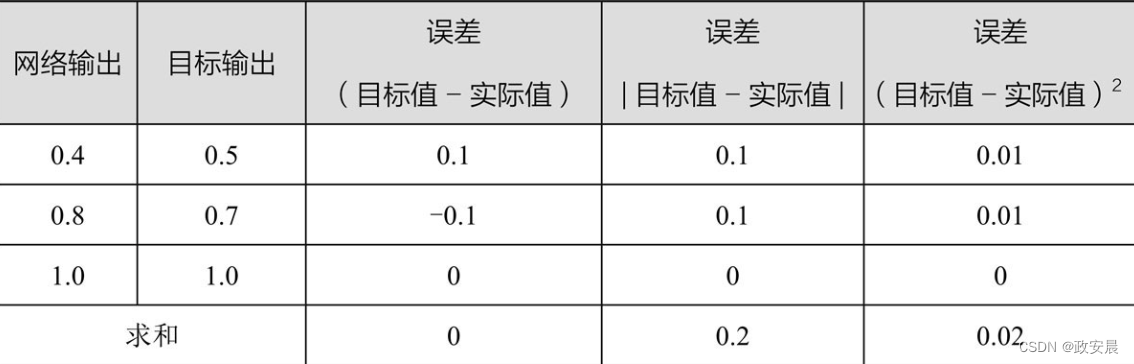
误差函数的第一个候选项是（目标值-实际值），非常简单。这似乎足够合理了，对吧？

如果你观察对所有节点的误差之和，以判断此时网络是否得到了很好的训练，你会看到总和为0！

这是如何发生的呢？

**A - **

很显然，由于前两个节点的输出值与目标值不同，这个网络没有得到很好的训练。但是，由于正负误差相互抵消，我们得到误差总和为0。总和为零意味着没有误差。然而即使正负误差没有完全互相抵消，这也很明显不符合实际情况，由此你也可以明白这不是一个很好的测量方法。

**B - **

为了纠正这一点，我们采用差的绝对值，即将其写成|目标值-实际值|，这意味着我们可以无视符号。由于误差不能互相抵消，这可能行得通。由于斜率在最小值附近不是连续的，这使得梯度下降方法无法很好地发挥作用，由于这个误差函数，我们会在V形山谷附近来回跳动，因此这个误差函数没有得到广泛应用。在这种情况下，即使接近了最小值，斜率也不会变得更小，因此我们的步长也不会变得更小，这意味着我们有超调的风险。

**C - **

第三种选择是差的平方，即（目标值-实际值）2。我们更喜欢使用第三种误差函数，而不喜欢使用第二种误差函数，原因有以下几点：

· 使用误差的平方，我们可以很容易使用代数计算出梯度下降的斜率。

· 误差函数平滑连续，这使得梯度下降法很好地发挥作用—没有间断，也没有突然的跳跃。

· 越接近最小值，梯度越小，这意味着，如果我们使用这个函数调节步长，超调的风险就会变得较小。

是否有第四个选项呢？

有，你可以构造各种各样的复杂有趣的代价函数。一些函数可能完全行不通，一些函数可能对特定类型的问题起作用，一些能够发挥作用的函数，可能由于额外的复杂度而有点不值得。

要使用梯度下降的方法，现在我们需要计算出误差函数相对于权重的斜率。

这需要微积分的知识，微积分使用精确的数学方式，计算出当一些变量改变时，其他应变量如何改变。例如，当在弹簧上施加一个伸展力时，弹簧的长度如何变化。

此处，我们感兴趣的是，误差函数是如何依赖于神经网络中的链接权重的。询问这个问题的另一种方式是—“误差对链接权重的改变有多敏感？”

咱们看下图：

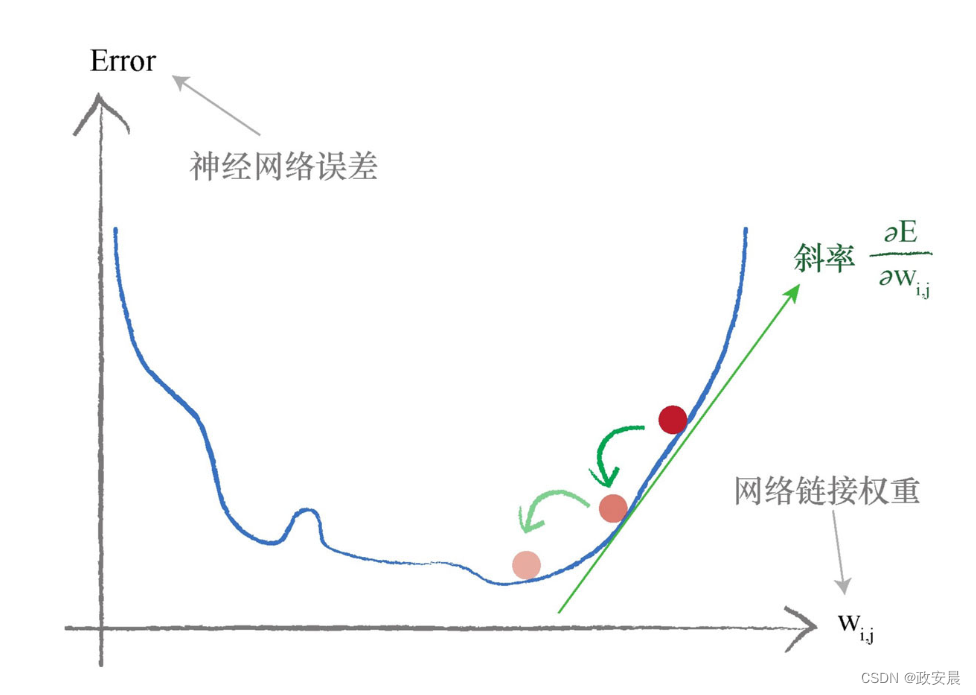
我们希望最小化的是神经网络的误差函数。我们试图优化的参数是网络链接权重。

在这个简单的例子中，我们只演示了一个权重，但是我们知道神经网络有众多权重参数。

下图显示了两个链接权重，这次，误差函数是三维曲面，这个曲面随着两个链接权重的变化而变化。你可以看到，我们努力最小化误差，现在，这有点像咱们这个系列第四篇文章提到的：在多山的地形中寻找一个山谷。

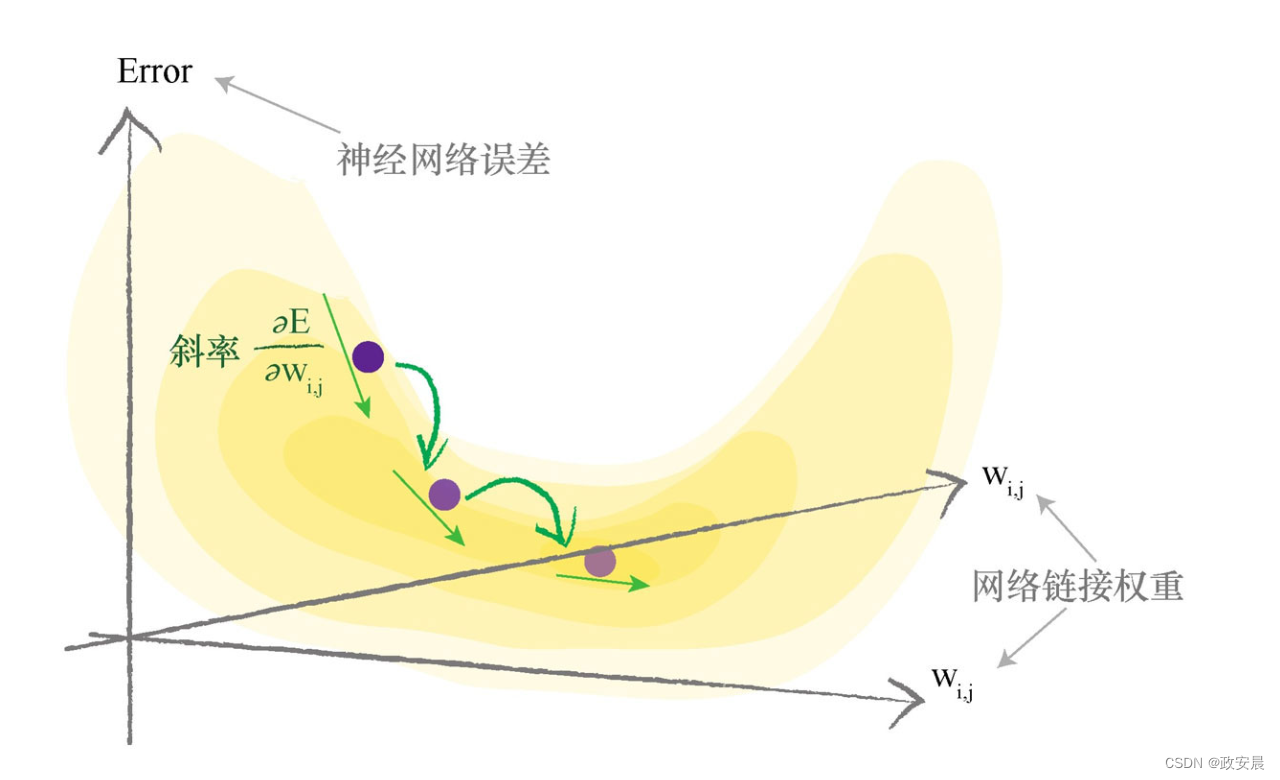
当函数具有多个参数时，要画出误差曲面相对较难，但是使用梯度下降寻找最小值的思想是相同的。

让我们使用数学的方式，写下想要取得的目标：

这个表达式表示了当权重wj,k改变时，误差E是如何改变的。这是误差函数的斜率，也就是我们希望使用梯度下降的方法到达最小值的方向。

在我们求解表达式之前，让我们只关注隐藏层和最终输出层之间的链接权重。下图突出显示了咱们所感兴趣的这个区域。我们将重回输入层和隐藏层之间的链接权重。

在进行微积分计算时，我们会时不时地返回来参照此图，以确保我们没有忘记每个符号的真正含义。小伙伴们不要被吓倒而裹足不前，这个过程并不困难，咱们在这个系列以前的文章中已经介绍了所有所需的概念。

首先，让我们展开误差函数，这是对目标值和实际值之差的平方进行求和，这是针对所有n个输出节点的和：

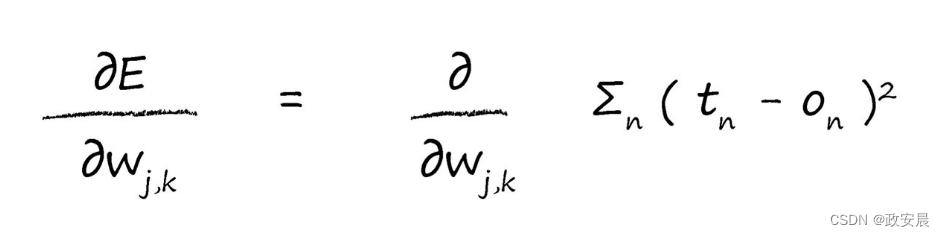
此处，我们所做的一切，就是写下实际的误差函数E。

注意，在节点n的输出只取决于连接到这个节点的链接，因此我们可以直接简化这个表达式。这意味着，由于这些权重是链接到节点k的权重，因此节点k的输出只取决于权重wj,k。

咱们可以使用另一种方式来看待这个问题，节点k的输出不依赖于权重wj,b，其中，由于b和k之间没有链接，因此b与k无关联。权重wj,b是连接输出节点b的链接权重，而不是输出节点k的链接权重。

这意味着，除了权重wj,k所链接的节点（也就是）外，我们可以从和中删除所有的，这就完全删除了令人厌烦的求和运算。这是一个很有用的技巧，值得保留下来收入囊中。

这意味着误差函数根本就不需要对所有输出节点求和。原因是节点的输出只取决于所连接的链接，就是取决于链接权重。这个过程在许多教科书中一略而过，这些教科书只是简单地声明了误差函数，却没有解释原因。

无论如何，咱们现在有了一个相对简单的表达式了。

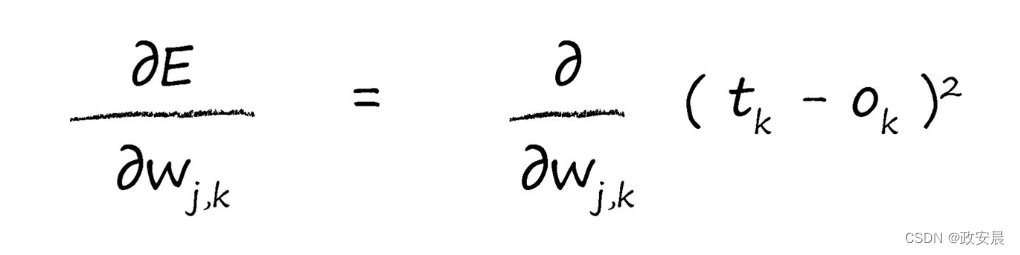
现在，我们将进行一点微积分计算。

的部分是一个常数，因此它不会随着wj,k的变化而变化。也就是说，不是wj,k的函数。仔细想想，如果真实示例所提供的目标值根据权重变化，就太让人匪夷所思了！由于我们使用权重前馈信号，得到输出值，因此这个表达式留下了我们所知的依赖于wj,k的部分。我们将使用链式法则，将这个微积分任务分解成更多易于管理的小块。

我们将使用链式法则，将这个微积分任务分解成更多易于管理的小块。

再看一下链式法则：

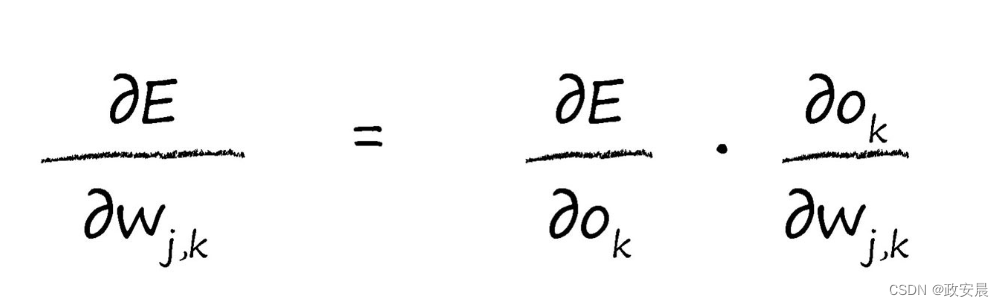
现在，我们可以反过来对相对简单的部分各个击破，我们对平方函数进行简单的微分，就很容易击破了第一个简单的项。这使我们得到了以下的式子：

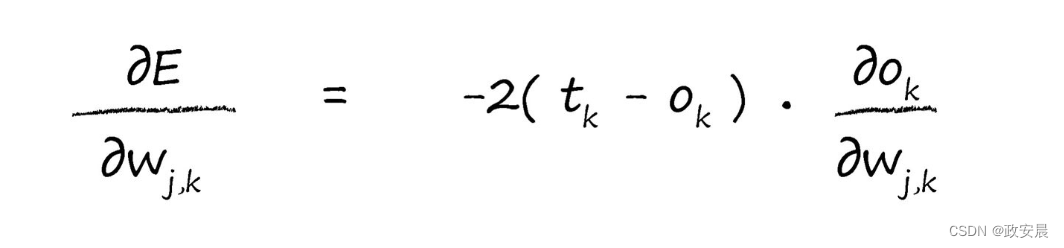
对于第二项，我们需要仔细考虑一下，但是无需考虑过久。是节点k的输出，如果你还记得，这是在连接输入信号上进行加权求和，在所得到结果上应用S函数得到的结果。让我们将这写下来，清楚地表达出来：

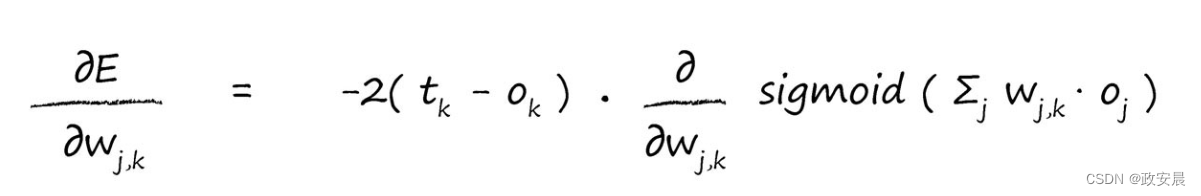
是前一个隐藏层节点的输出，而不是最终层的输出。

对S函数求微分，这对我们而言是一种非常艰辛的方法，但是，其他人已经完成了这项工作。我们可以只使用众所周知的答案，就像全世界的数学家每天都在做的事情一样即可（细节这里不赘述啦）。

在微分后，一些函数变成了非常可怕的表达式，S函数微分后，可以得到一个非常简单、易于使用的结果。在神经网络中，这是S函数成为大受欢迎的激活函数的一个重要原因。

因此，让我们应用这个酷炫的结果，得到以下的表达式：

这个额外的最后一项是什么呢？由于在sigmoid()函数内部的表达式也需要对进行微分，因此我们对S函数微分项再次应用链式法则。这也非常容易，答案很简单，为。

在写下最后的答案之前，让我们把在前面的2去掉，我们只对误差函数的斜率方向感兴趣，这样我们就可以使用梯度下降的方法，因此可以去掉2。只要我们牢牢记住需要什么，在表达式前面的常数，无论是2、3还是100，都无关紧要。因此，去掉这个常数，让事情变得简单。

这就是我们一直在努力要得到的最后答案，这个表达式描述了误差函数的斜率，这样我们就可以调整权重了：

这就是我们一直在寻找的神奇表达式，也是训练神经网络的关键。

这个表达式值得再次回味，颜色标记有助于显示出表达式的各个部分。

第一部分，非常简单，就是（目标值-实际值），我们对此已经很清楚了。

在sigmoid中的求和表达式也很简单，就是进入最后一层节点的信号，我们可以称之为ik，这样它看起来比较简单。这是应用激活函数之前，进入节点的信号。

最后一部分是前一隐藏层节点j的输出。读者要有一种意识，明白在这个斜率的表达式中，实际涉及哪些信息并最终优化了权重，因此小伙伴们值得仔细观察这些表达式、这些项。

咱们还需要做最后一件事情。我们所得到的这个表达式，是为了优化隐藏层和输出层之间的权重。现在，我们需要完成工作，为输入层和隐藏层之间的权重找到类似的误差斜率。

同样，我们可以进行大量的代数运算，但是不必这样做。我们可以很简单地使用刚才所做的解释，为感兴趣的新权重集重新构建一个表达式：

· 第一部分的（目标值-实际值）误差，现在变成了隐藏层节点中重组的向后传播误差，正如在前面所看到的那样。我们称之为ej。

· sigmoid部分可以保持不变，但是内部的求和表达式指的是前一层，因此求和的范围是所有由权重调节的进入隐藏层节点j的输入。我们可以称之为ij。

· 现在，最后一部分是第一层节点的输出oi，这碰巧是输入信号。

这种巧妙的方法，简单利用问题中的对称性构建了一个新的表达式，避免了大量的工作。这种方法虽然很简单，但却是一种很强大的技术，一些天赋异禀的数学家和科学家都使用这种技术。你肯定可以使用这个技术，给你的队友留下深刻印象。

因此，我们一直在努力达成的最终答案的第二部分如下所示，这是我们所得到误差函数斜率，用于输入层和隐藏层之间权重调整。

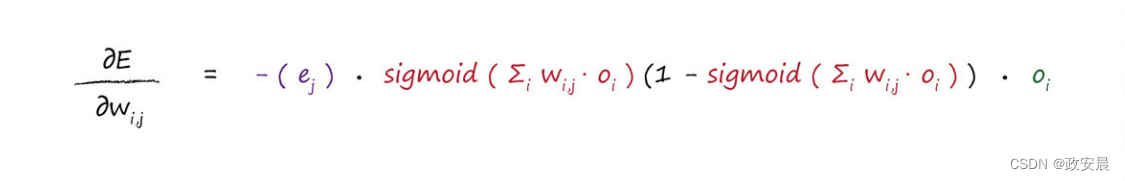
现在，我们得到了关于斜率的所有关键的神奇表达式，可以使用这些表达式，在应用每层训练样本后，更新权重，在接下来的内容中我们将会看到这一点。

记住权重改变的方向与梯度方向相反，正如我们在先前的图中清楚看到的一样。我们使用学习因子，调节变化，我们可以根据特定的问题，调整这个学习因子。当我们建立线性分类器，作为避免被错误的训练样本拉得太远的一种方式，同时也为了保证权重不会由于持续的超调而在最小值附近来回摆动，我们都发现了这个学习因子。让我们用数学的形式来表达这个因子。

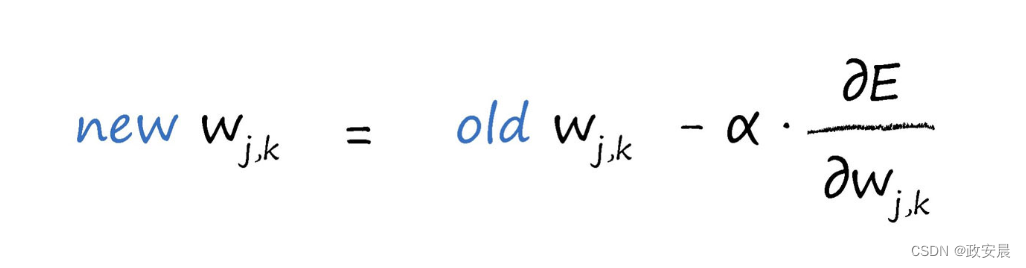
更新后的权重wj, k是由刚刚得到误差斜率取反来调整旧的权重而得到的。正如我们先前所看到的，如果斜率为正，我们希望减小权重，如果斜率为负，我们希望增加权重，因此，我们要对斜率取反。符号α是一个因子，这个因子可以调节这些变化的强度，确保不会超调。我们通常称这个因子为学习率。

这个表达式不仅适用于隐藏层和输出层之间的权重，而且适用于输入层和隐藏层之间的权重。差值就是误差梯度，我们可以使用上述两个表达式来计算这个误差梯度。

如果我们试图按照矩阵乘法的形式进行运算，那么我们需要看看计算的过程。为了有助于理解，我们将按照以前那样写出权重变化矩阵的每个元素。

由于学习率只是一个常数，并没有真正改变如何组织矩阵乘法，因此我们省略了学习率α。

权重改变矩阵中包含的值，这些值可以调整链接权重wj, k，这个权重链接了当前层节点j与下一层节点k。你可以发现，表达式中的第一项使用下一层（节点k）的值，最后一项使用前一层（节点j）的值。

仔细观察上图，你就会发现，表达式的最后一部分，也就是单行的水平矩阵，是前一层oj的输出的转置。颜色标记显示点乘是正确的方式。如果你不能确定，请尝试使用另一种方式的点乘，你会发现这是行不通的。

因此，权重更新矩阵有如下的矩阵形式，这种形式可以让我们通过计算机编程语言高效地实现矩阵运算。

实际上，这不是什么复杂的表达式。由于我们简化了节点输出，那些sigmoids已经消失了。

示例

我们来演示几个有数字的示例，让读者看看这种权重更新的方法是可以成功的。下面的网络是我们之前演示过的一个，但是这次，我们添加了隐藏层第一个节点oj=1和隐藏层第二个节点oj=2的示例输出值。这些数字只是为了详细说明这个方法而随意列举的，读者不能通过输入层前馈信号正确计算得到它们：

我们要更新隐藏层和输出层之间的权重w1,1。当前，这个值为2.0。

让我们再次写出误差斜率（方便比照看）。

让我们一项一项地进行运算：

· 第一项（tk-ok）得到误差e1=0.8。

· S函数内的求和Σjwj,koj为（2.0×0.4）+（3.0 * 0.5）=2.3。

*· sigmoid 1/(1+e -2.3) 为0.909。中间的表达式为0.909 （1-0.909）=0.083。

· 由于我们感兴趣的是权重w1,1，其中j=1，因此最后一项oj也很简单，也就是oj=1。此处，oj值就是0.4。

将这三项相乘，同时不要忘记表达式前的负号，最后我们得到-0.0265。

如果学习率为0.1，那么得出的改变量为-（0.1 * -0.02650）=+0.002650。因此，新的w1,1就是原来的2.0加上0.00265等于2.00265。

虽然这是一个相当小的变化量，但权重经过成百上千次的迭代，最终会确定下来，达到一种布局，这样训练有素的神经网络就会生成与训练样本中相同的输出。

咱们就这样完成了这个例子。

结论

1. 神经网络的误差是内部链接权重的函数。

2. 改进神经网络，意味着通过改变权重减少这种误差。

3. 直接选择合适的权重太难了。另一种方法是，通过误差函数的梯度下降，采取小步长，迭代地改进权重。所迈出的每一步的方向都是在当前位置向下斜率最大的方向，这就是所谓的梯度下降。

4. 使用微积分可以很容易地计算出误差斜率。

至此，咱们已经完成了零基础认知人工智能的神经网络全系列的文章啦。