系列文章链接:
AI艺术的背后:详解文本生成图像模型【基于 VQ-VAE】
AI艺术的背后:详解文本生成图像模型【基于GAN】
AI艺术的背后:详解文本生成图像模型【基于Diffusion Model】
导言
AI 艺术生成已经开始走进大众的视野中。在过去一年里,出现了大量的文本生成图像模型,尤其是随着 Stable Diffusion 以及 Midjourney 的出现,带起了一股 AI 艺术创作热潮,甚至很多艺术家也开始尝试用 AI 来辅助艺术创作。在本文中,将会系统梳理近几年出现的文本生成图像算法,帮助大家深入了解其背后的原理。
基于 Diffusion Model
不同于 VQ-VAE,VQ-GAN,扩散模型是当今文本生成图像领域的核心方法,当前最知名也最受欢迎的文本生成图像模型 Stable Diffusion,Disco-Diffusion,Mid-Journey,DALL-E2 等等,均基于扩散模型。在这部分,会对扩散模型的原理以及基于扩散模型的算法进行详细的介绍。
Diffusion Model
回忆上文提到的 VQ-VAE 以及 VQ-GAN,都是先通过编码器将图像映射到中间潜变量,然后解码器在通过中间潜变量进行还原。实际上,扩散模型做的事情本质上是一样的,不同的是,扩散模型完全使用了全新的思路来实现这个目标。
在扩散模型中,主要有两个过程组成,前向扩散过程,反向去噪过程,前向扩散过程主要是将一张图片变成随机噪音,而逆向去噪过程则是将一张随机噪音的图片还原为一张完整的图片。
为了帮助理解,这里选择最经典的扩散模型进行介绍,关于扩散模型的具体推导,可以参考。
前向扩散过程
前向扩散过程的本质就是在原始图像上,随机添加噪音,通过 T 步迭代,最终将原始图片的分布变成标准高斯分布
I
∼
N
(
0
,
1
)
\text I \sim N(0, 1)
I∼N(0,1) 具体来说,给定初始数据分布
x
0
∼
p
(
x
)
x_0 \sim p(x)
x0∼p(x) ,增加噪声的过程可以定义为如下公式:
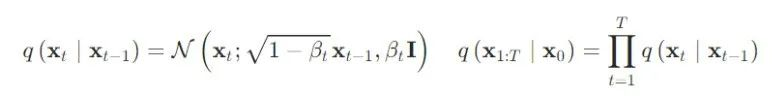
其中:
{
β
t
∈
(
0
,
1
)
}
t
=
1
t
\{\beta_t\in(0,1)\}_{t=1}^t
{βt∈(0,1)}t=1t ,在这个过程中,随着 t 的不断增大,最终数据分布 x 变成了一个各向独立的高斯分布。
值得注意的是,这里正向扩散的过程,由于参数
β
t
\beta_t
βt 是预先定义好的,前向过程没有任何需要学习的参数,因此每一时刻的结果都可以直接计算出来,这里首先定义
α
t
=
1
−
β
t
,
α
‾
t
=
∏
i
=
1
T
α
i
\alpha_t = 1-\beta_t,\overline \alpha_t= \prod _{i = 1}^T\alpha_i
αt=1−βt,αt=∏i=1Tαi,
则: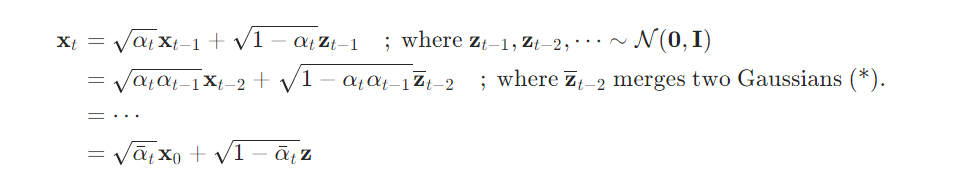
因此得到前向扩散过程的分布表达式为:
逆向扩散过程
逆向过程就是还原的过程,也就是从高斯噪声中恢复原始分布的过程,实际上,只要学习
q
(
x
t
−
1
∣
x
t
)
q(x_{t-1}|x_t)
q(xt−1∣xt) 分布即可,可以通过一个可学习的神经网络来对其进行拟合,其定义如下:
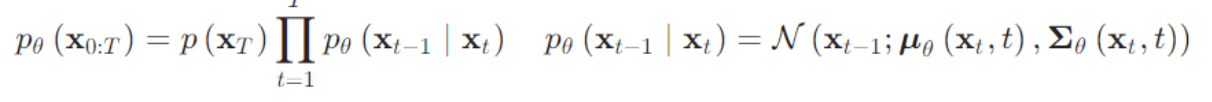
其中,
μ
θ
(
x
t
,
t
)
,
Σ
θ
(
x
t
,
t
)
\mu_\theta(x_t, t), \Sigma_\theta(x_t, t)
μθ(xt,t),Σθ(xt,t) 由于无法直接估计,因此一般会使用神经网络模型来进行逼近,需要注意的是,在原始论文中,方差是无需训练的,被预选设置好了:
Σ
θ
(
x
t
,
t
)
=
σ
t
2
I
\Sigma_\theta(x_t, t)=\sigma_t^2\text I
Σθ(xt,t)=σt2I ,而这里
σ
t
2
=
β
‾
t
\sigma_t^2 = \overline\beta_t
σt2=βt
由于隐马尔可夫的性质,
x
0
,
x
1
,
.
.
.
,
x
T
x_0, x_1, ..., x_T
x0,x1,...,xT 是条件独立的,因此
q
(
x
t
−
1
∣
x
t
)
=
q
(
x
t
−
1
∣
x
t
,
x
0
)
q(x_{t-1}|x_t)=q(x_{t-1}|x_t, x_0)
q(xt−1∣xt)=q(xt−1∣xt,x0) ,而这里,后一项则可以直接使用一个表达式来表达出来,从而使得的们可以进行后面的优化计算,这里将表达式写成:
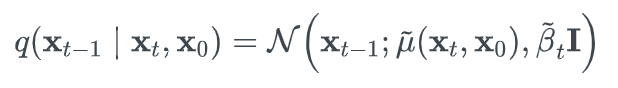
通过推导可以得到:(详细可以看[13,14])
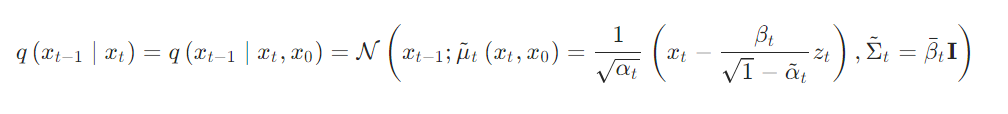
扩散模型本质上也是在学习数据分布,因此其对数似然可以表示为: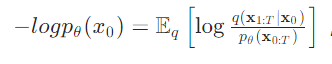
最终,其 loss 可以表示为[13,14]: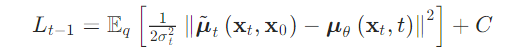
经过化简,可以得到最后 loss 表达形式,从公式形态来看,其目标就是在预测每一步的噪音: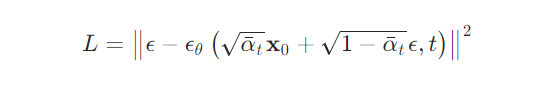
训练流程
直观上理解,扩散模型其实是通过一个神经网络 ,来预测每一步扩散模型中所添加的噪音,其算法流程如下:
在完成训练之后,只需要通过重参数化技巧,进行采样操作即可,具体流程如上边右图所示,通过不断的「减去」模型预测的噪音,可以逐渐的生成一张完整的图片。
Classifier-Free Guidance Diffusion
基于传统的扩散模型,后续又有一些改进操作,这些改进操作使得扩散模型被广泛的应用于文本生成图像任务中。其中,最常用的改进版本为 Classifier-Free Guidance Diffusion。
上述扩散模型通过
ϵ
θ
(
x
t
)
\epsilon_\theta(x_t)
ϵθ(xt) 来对噪音进行估计,而引导扩散模型,则需要将引导条件
y
y
y,加入到模型输入中,因此到的
ϵ
θ
(
x
t
,
y
)
\epsilon_\theta(x_t, y)
ϵθ(xt,y) ,而 Classifier-Free Guidance Diffusion 则结和了条件和无条件噪声估计模型,其定义为:
ϵ
^
θ
(
x
t
∣
y
)
=
ϵ
θ
(
x
t
)
+
s
⋅
(
ϵ
θ
(
x
t
,
y
)
−
ϵ
θ
(
x
t
)
)
\hat\epsilon_\theta(x_t|y) = \epsilon_\theta(x_t) + s\cdot(\epsilon_\theta(x_t, y)-\epsilon_\theta(x_t))
ϵ^θ(xt∣y)=ϵθ(xt)+s⋅(ϵθ(xt,y)−ϵθ(xt))
这样做的优点是训练过程非常稳定,且摆脱了分类器的限制(实际上等价于学习了一个隐含的分类器),缺点是,成本比较高,相当于每次要生成两个输出,尽管如此,后面的大部份知名文本生成图像模型,都是基于这个方法进行的。
GLIDE
GLIDE 使用了文本作为条件,来实现文本引导的扩散模型,在文本引导上面,文中主要使用了两种策略,Classifier-Free Diffusion Guidence 以及 CLIP 来作为条件监督,同时使用了更大的模型,在数据量上,和DALL-E 相似。
GLIDE 的核心就是 Classifier-Free Diffusion Guidence,其使用文本描述作为引导,来训练一个扩散模型,其定义为:
ϵ
^
θ
(
x
t
∣
y
)
=
ϵ
θ
(
x
t
∣
∅
)
+
s
⋅
(
ϵ
θ
(
x
t
,
y
)
−
ϵ
θ
(
x
t
∣
∅
)
)
\hat\epsilon_\theta(x_t|y) = \epsilon_\theta(x_t|\emptyset) + s\cdot(\epsilon_\theta(x_t, y)-\epsilon_\theta(x_t|\emptyset))
ϵ^θ(xt∣y)=ϵθ(xt∣∅)+s⋅(ϵθ(xt,y)−ϵθ(xt∣∅))
其中,y是一段文本描述。
由于 GLIDE 方法提出较早,相对于现有很多方法,GLIDE 模型的效果并不是很好,下面是 GLIDE 生成的图像示例。
GLIDE 还支持通过 选取区域+文本Prompt 来对图像进行编辑操作,可以看出效果也不错。使用过程中,只需要将遮蔽区域进行 mask,以及剩下的图片一起送入到网络中,即可产生补全之后的图片。
此外,GLIDE 的语义理解能力并不是很强,在一些少见的文本描述下,很难产生合乎逻辑的图像,而 DALL-E2 在这方面的能力上,要远超 GLIDE
DALL-E2
DALL-E2 是 OpenAI 最新 AI 生成图像模型,其最大的特色是模型具有惊人的理解力和创造力, 其参数大约 3.5B , 相对于上一代版本,DALL-E2 可以生成4倍分倍率的图片,且非常贴合语义信息。作者使用了人工评测方法,让志愿者看1000张图,71.7% 的人认为其更加匹配文本描述 ,88.8% 认为画的图相对于上一代版本更加好看。
DALL-E2 由三个模块组成:
- CLIP模型,对齐图片文本表征
- 先验模型,接收文本信息,将其转换成 CLIP 图像表征
- 扩散模型,接受图像表征,来生成完整图像
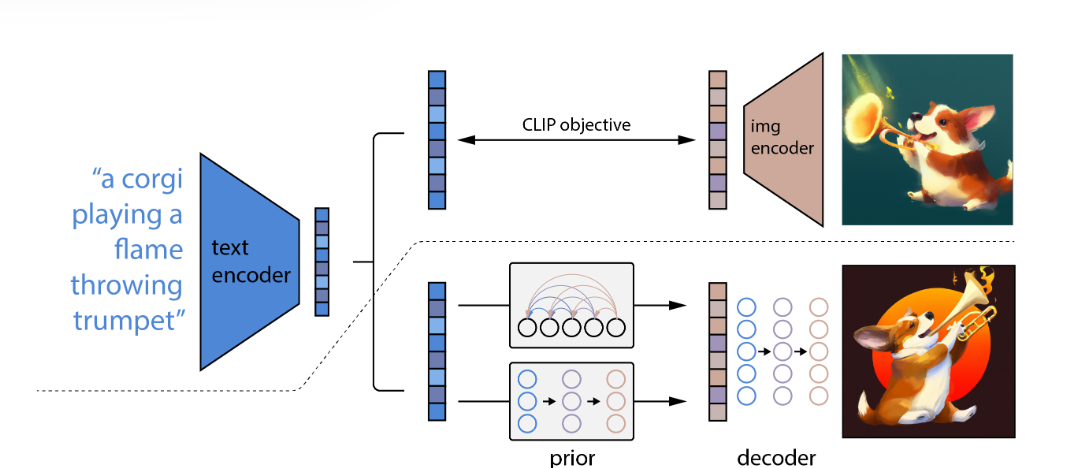
DALL-E2 的训练过程为:
- 训练一个 CLIP 模型,使其能够对齐文本和图片特征。
- 训练一个先验模型,由自回归模型或者一个扩散先验模型(实验证明,扩散先验模型表现更好),其功能是将文本表征映射为图片表征。
- 训练一个扩散解码模型,其目标是根据图片表征,还原原始图片。
在训练完成之后,推理过程就比较直接了,首先使用CLIP 文本编码器,获得文本编码,之后使用先验模型将文本编码映射为图片编码,最后使用扩散解码器用图片编码生成完整图片。注意这里扩散解码模型使用的是经过修改的 GLIDE 扩散模型,其生成的图像尺寸为 64×64,然后使用两个上采样扩散模型将其上采样至 256×256,以及 1024×1024.
DALL-E2 原论文中也提到了其许多不足,例如容易将物体和属性混淆,无法精确的将文本放置到图像中,然而,这些都无法阻止大家对文本生成图像的热情,DALL-E2 也被广泛应用到各种艺术创作过程中。
Imagen
在 DALL-E2 提出没多久,Google 就提出了一个新的文本生成图像模型 Imagen ,论文中提到,其生成的图片相对于 DALL-E2 真实感和语言理解能力都更加强大(使用一种新的评测方法 DrawBench)。
Imagen 的图像生成流程和 DALL-E2 非常像,首先将文本进行编码表征,之后使用扩散模型将表征映射成为完整图像,同时会通过两个扩散模型来进一步提高分辨率。与 DALL-E2 不同的是,Imagen 使用了 T5-XXL 模型直接编码文本信息,然后使用条件扩散模型,直接用文本编码生成图像。因此,在 Imagen 中,无需学习先验模型。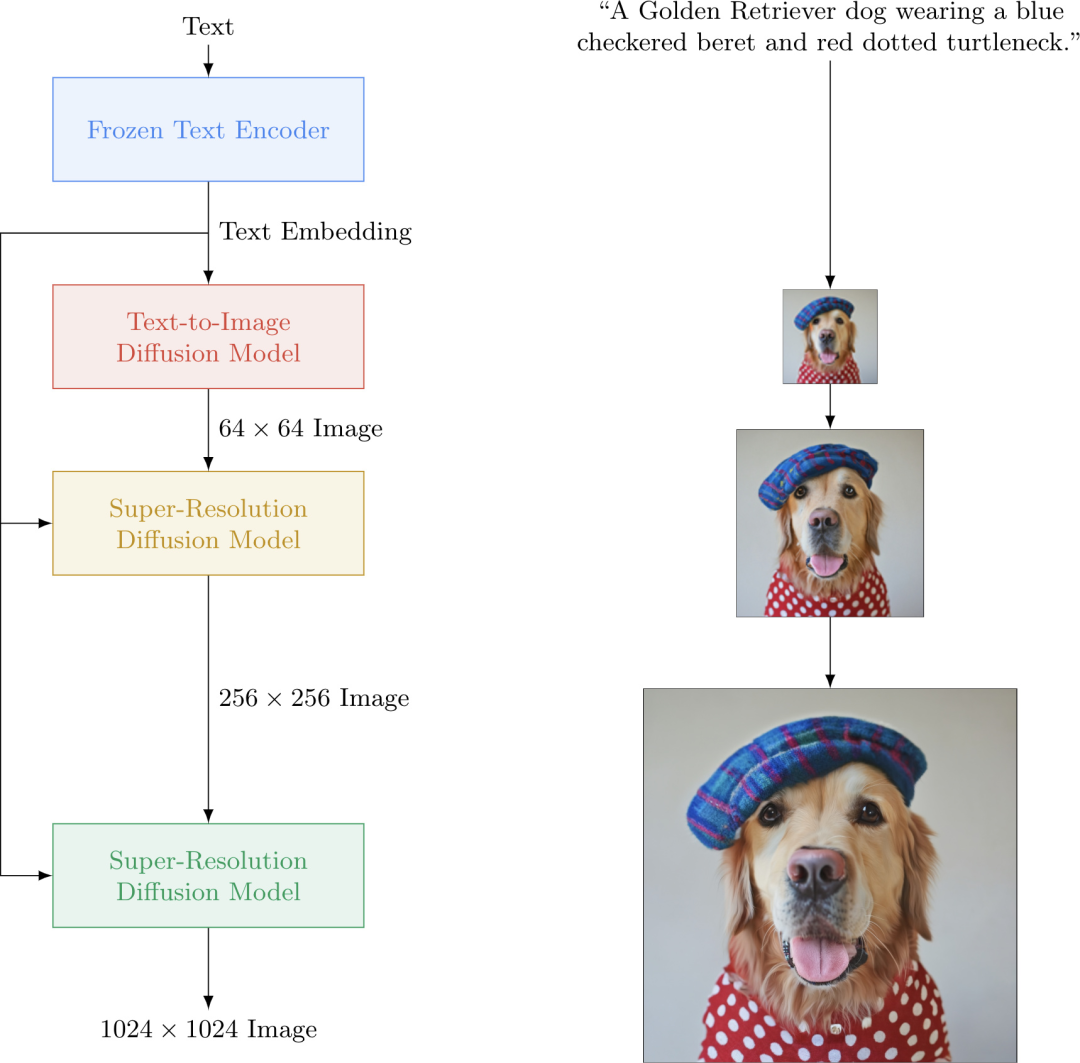
由于直接使用 T5-XXL 模型,其语义知识相对于 CLIP 要丰富很多(图文匹配数据集数量要远远少于纯文本数据集数量),因此 Imagen 相对于 DALL-E2 在语义保真度上做的更好。同时,作者也发现,增大语言模型,可以有效的提高样本的语义保真度。
Stable Diffusion
Stable Diffusion 是由 Stability.ai 于近期开放的文本生成图像模型,由于其交互简单,生成速度快,极大的降低了使用门槛,而且同时还保持了令人惊讶的生成效果,从而掀起了一股 AI 创作热潮 。 ©本文作者用Stable Diffusion 生成的图片
©本文作者用Stable Diffusion 生成的图片
Stable Diffusion 是基于之前 Latent Diffusion 模型进行改进的,上文中提到的扩散模型的特点是反向去噪过程速度较慢,其扩散过程是在像素空间进行,当图片分辨率变大时,速度会变得非常慢。而 Latent Diffusion 模型则考虑在较低维度的潜在空间中,进行扩散过程,这样就极大的减轻了训练以及推理成本。
Stable Diffusion 由三个部分组成:
- VAE 其作用是将图像转换为低维表示形式,从而使得扩散过程是在这个低维表征中进行的,扩散完成之后,在通过VAE 解码器,将其解码成图片。
- U-Net 网络 U-Net 是扩散模型的主干网络,其作用是对噪音进行预测,从而实现反向去噪过程
- 文本编码器CLIP 主要负责将文本转换为U-Net可以理解的表征形式,从而引导U-Net进行扩散。
Stable Diffusion 的具体推理过程如下图所示 ,首先使用 CLIP 将文本转换为表征形式,然后引导扩散模型 U-Net 在低维表征(64×64)上进行扩散过程,之后将扩散之后的低维表征送入到 VAE 中的解码器部分,从而实现图像生成。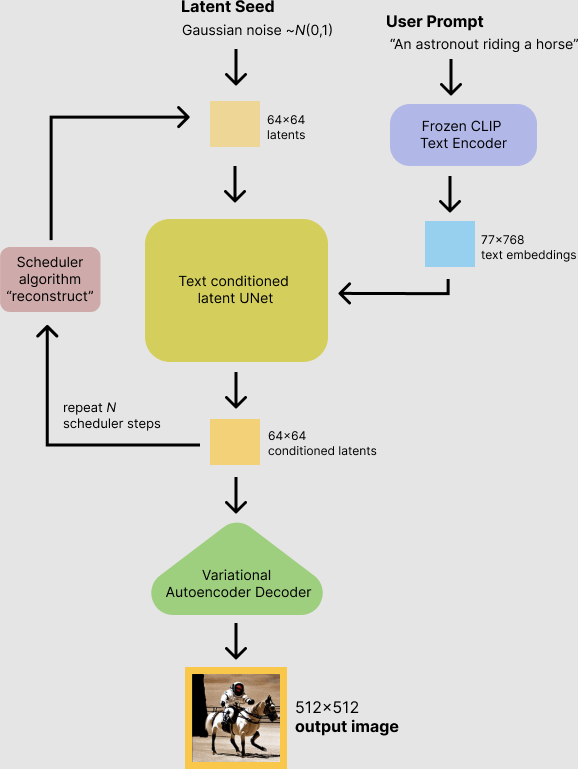
模型试玩
了解了文本生成图像背后的算法原理,也可以试玩一下开源模型,这里列举了一些当前比较流行且易于使用的模型链接,其中,效果最好且交互最便捷的则是 Stable Diffusion 和 MidJourney。
VQGAN-CLIP
https://nightcafe.studio/
DALL-E-Mini
https://huggingface.co/spaces/dalle-mini/dalle-mini
DALL-E2
https://github.com/openai/dall-e (需要等 Waitlist)
Stable Diffusion
https://beta.dreamstudio.ai/dream
Disco-Diffusion
https://colab.research.google.com/github/alembics/disco-diffusion/blob/main/Disco_Diffusion.ipynb
MidJourney
https://www.midjourney.com/home/
NUWA
https://nuwa-infinity.microsoft.com/#/ (暂未开放,可以保持关注)
版权归原作者 NLP_wendi 所有, 如有侵权,请联系我们删除。