【JavaSE|数据结构】排序算法之快速排序

⭐️前面的话⭐️

本篇文章带大家认识排序算法——快速排序，从名字上就能看出来，因为它比较快，所以叫做快速排序，它也是一种基于比较的排序算法，本文将以图解动图的形式解读快速排序，代码实现语言为java。

📒博客主页：未见花闻的博客主页
🎉欢迎关注🔎点赞👍收藏⭐️留言📝
📌本文由未见花闻原创，CSDN首发！
📆首发时间：🌴2022年2月24日🌴
✉️坚持和努力一定能换来诗与远方！
💭参考书籍：📚《Java核心技术》，📚《Java编程思想》，📚《数据结构》
💬参考在线编程网站：🌐牛客网🌐力扣
博主的码云gitee，平常博主写的程序代码都在里面。
博主的github，平常博主写的程序代码都在里面。
🙏作者水平很有限，如果发现错误，一定要及时告知作者哦！感谢感谢！

📌导航小助手📌

题外话： 本文所有的排序算法设计都基于升序排列，降序排列的思路是一样的，只需将思路调换一下即可。

1.快速排序原理

1.1快速排序

快速排序的核心思想就是从数组中找一个基准值 ，然后以该基准值，将比基准值小的元素排在基准值左边，比基准值大的元素排在基准值右边，此时基准值在数组中的排序位置已经确定了，再对基准值左边和右边的序列以相同的方式重新找基准值并将比基准值小的排左边，大的排右边，直到只剩下一个元素，此时所有的元素排序位置都确定了，那么数组排序就完成了。

1.2找基准

1.2.1选取基准值

我们知道找基准值和确定基准值位置是快速排序的关键，那么如何找基准值和确定其位置呢？

找基准值常常使用以下几个方法：

1. 使用数组边界的元素作为基准值，即最左边的元素或者最右边的元素。
2. 随机取值，即从数组中随机选取一个元素作为基准值，不稳定，排序速度要看运气。
3. 几个数取中间值作为基准值，常用是三数取中，即从数组边界两个元素和数组中间元素选择一个大小居中的元素作为基准值。

找基准值我们以第一个最简单的方法为例，使用数组第一个元素作为基准值，确定了那个数组的基准值，然后就是确定基准值的位置了，就是将比基准值小的元素放在左边，大的放在右边。

1.2.2确定基准值位置并实现快速排序

对于基准值位置调整常见方法有：

1. 挖坑法
2. Hoare 法
3. 前后遍历法

从本质上来说挖坑法与Hoare 法是一样的，只不过前者是填坑，后者是交换，以挖坑法为例，我们来实现以下快速排序。

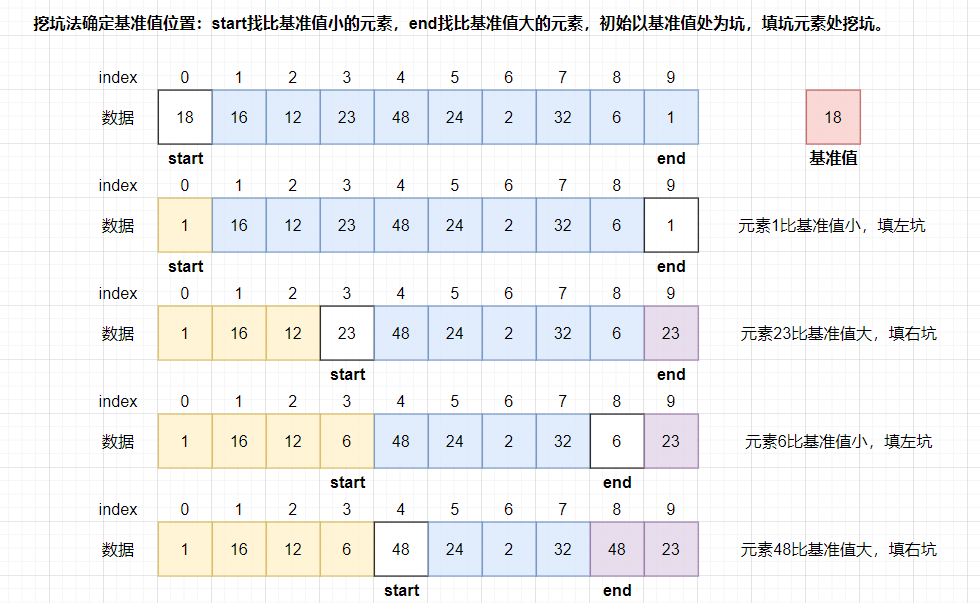
挖坑法找基准实现快速排序步骤如下：

1. 以数组第一个元素为基准值。
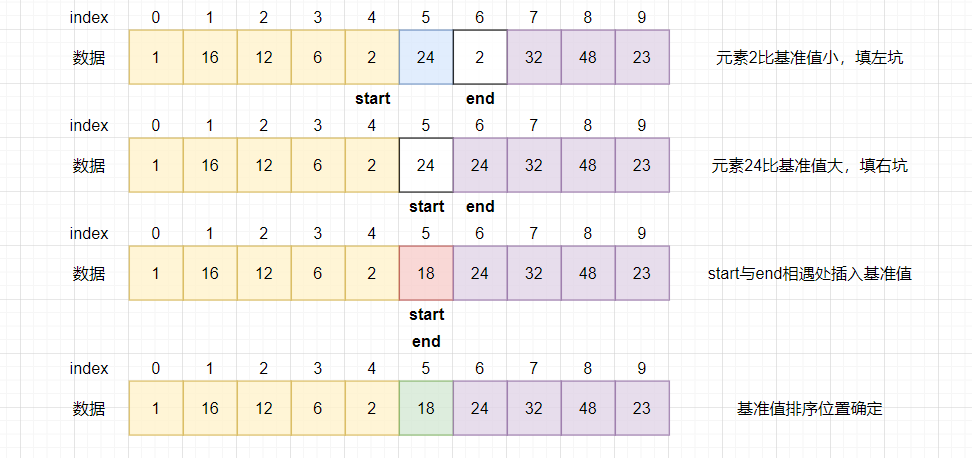
2. 挖坑法确定基准值位置：start找比基准值小的元素，end找比基准值大的元素，初始以基准值处为坑，填坑元素处挖坑，就是左边的坑填比基准值小的元素，右边的坑填比基准值大的元素。
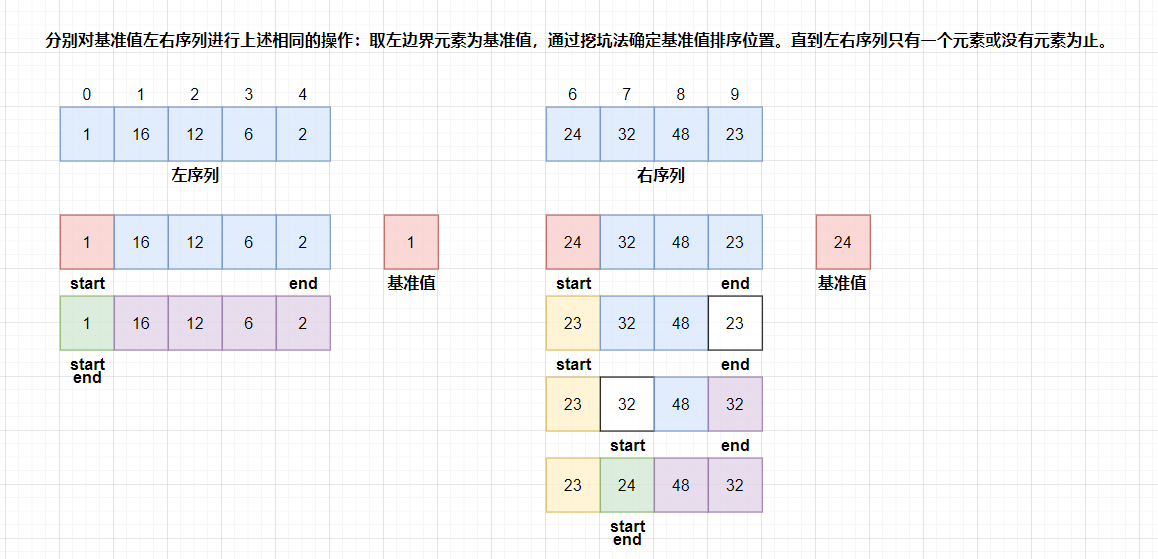
3. 分别对基准值左右序列进行上述相同的操作：取左边界元素为基准值，通过挖坑法确定基准值排序位置。直到左右序列只有一个元素或没有元素为止。此时数组已经有序了。

总的来说，实现快速排序有三步，第一找基准值， 第二确定基准值位置，第三对基准值左右序列进行相同的找基准方法，最终会使所有的元素有序。
还是请出我们的老朋友[18, 16, 12, 23, 48, 24, 2, 32, 6, 1]为例！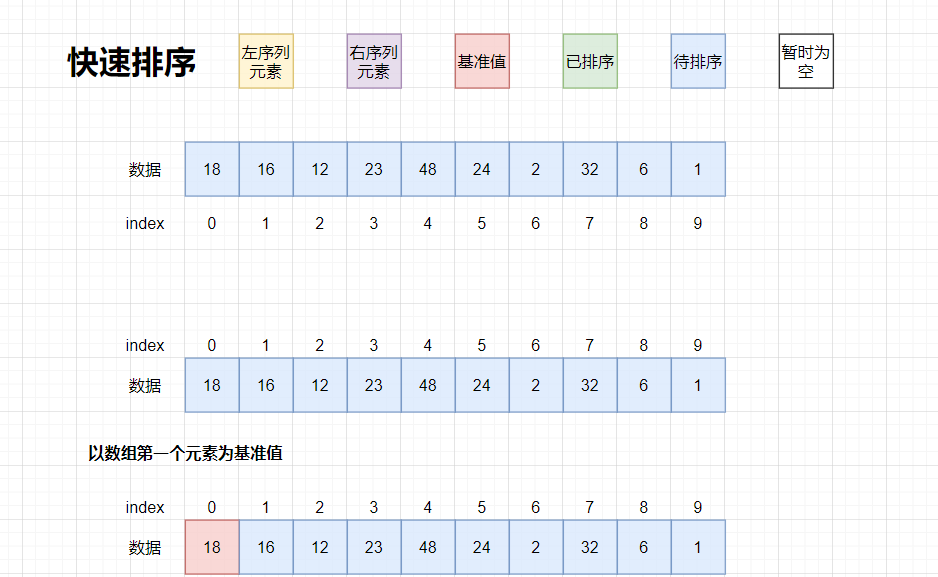






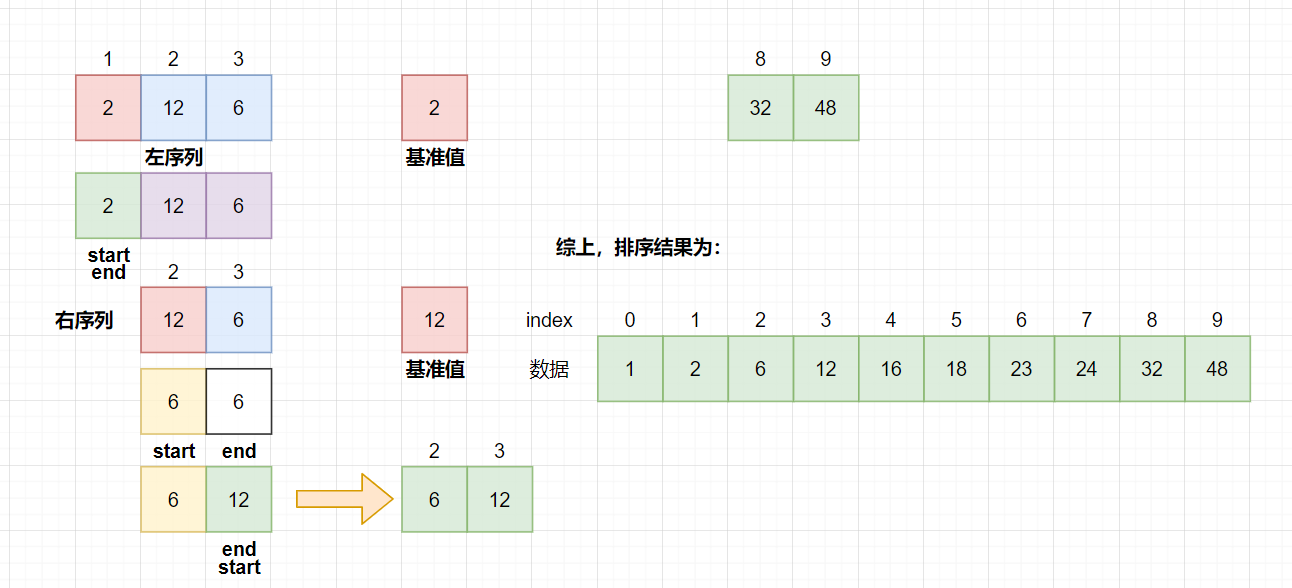
挖坑法实现代码：

/**
     * 挖坑法找基准
     * @param array 待排序数组对象
     * @param left 左边界
     * @param right 右边界
     * @return 基准值下标
     */publicinttest2(int[] array,int left,int right){//取左边界元素为基准值，该位置“挖坑”int pivot = array[left];int start = left;int end = right;while(start < end){//从右边界end开始找比基准值小的元素while(start < end && array[end]>= pivot){
                end--;}//填上一个坑start，此时end位置挖坑
            array[start]= array[end];//从左边界start开始找比基准值大的元素while(start < end && array[start]<= pivot){
                start++;}//填上一个坑end，此时start位置挖坑
            array[end]= array[start];}//start与end相等时的位置，即基准值位置
        array[start]= pivot;return start;}

基于挖坑法实现的快速排序代码：

/**
     * 快速排序
     * @param array 待排序数组对象
     */publicvoidquickSort(int[] array){quickSortFunc(array,0, array.length-1);}privatevoidquickSortFunc(int[] array,int start,int end){if(start >= end)return;//1.找基准int pivotIndex =findPivot(array, start, end);//2.快排基准左边元素序列quickSortFunc(array, start, pivotIndex-1);//3.快排基准右边元素序列quickSortFunc(array, pivotIndex+1, end);}/**
     * 找基准
     * @param array 待排序数组对象
     * @param left 左边界
     * @param right 右边界
     * @return 基准值下标
     */privateintfindPivot(int[] array,int left,int right){//取左边界元素为基准值，该位置“挖坑”int pivot = array[left];int start = left;int end = right;while(start < end){//从右边界end开始找比基准值小的元素while(start < end && array[end]>= pivot){
                end--;}//填上一个坑start，此时end位置挖坑
            array[start]= array[end];//从左边界start开始找比基准值大的元素while(start < end && array[start]<= pivot){
                start++;}//填上一个坑end，此时start位置挖坑
            array[end]= array[start];}//start与end相等时的位置，即基准值位置
        array[start]= pivot;return start;}

下面我们再来了解一下Hoare 法确定基准值位置：

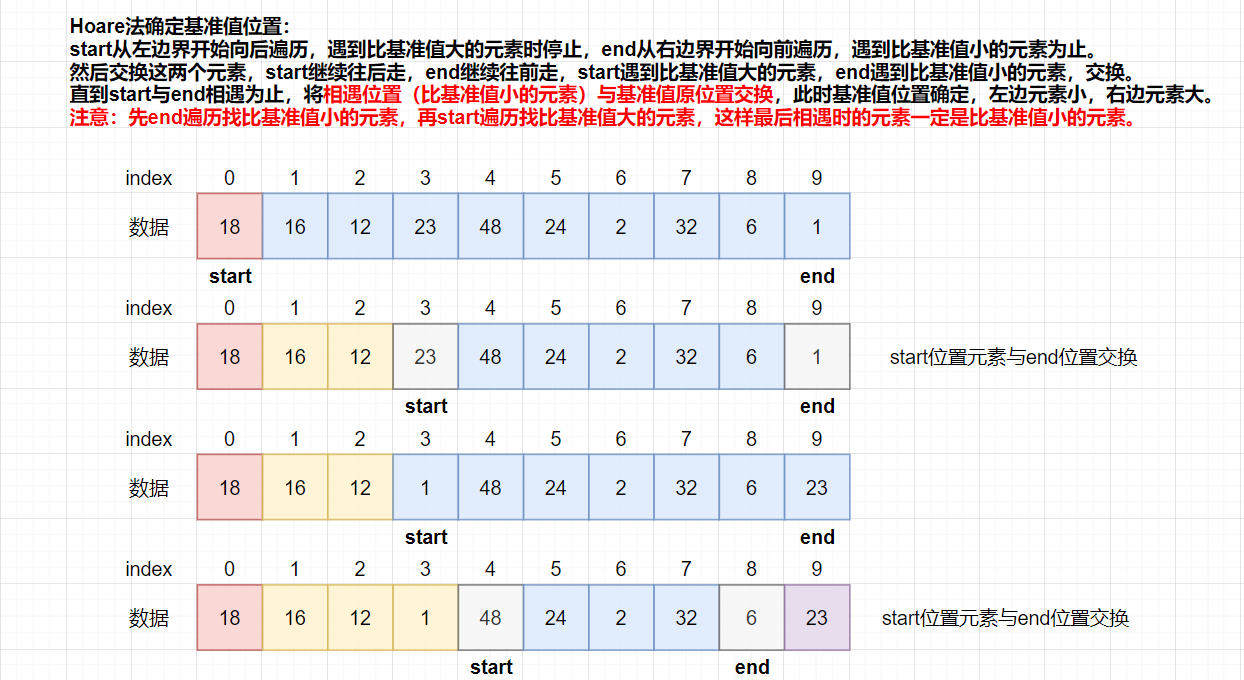
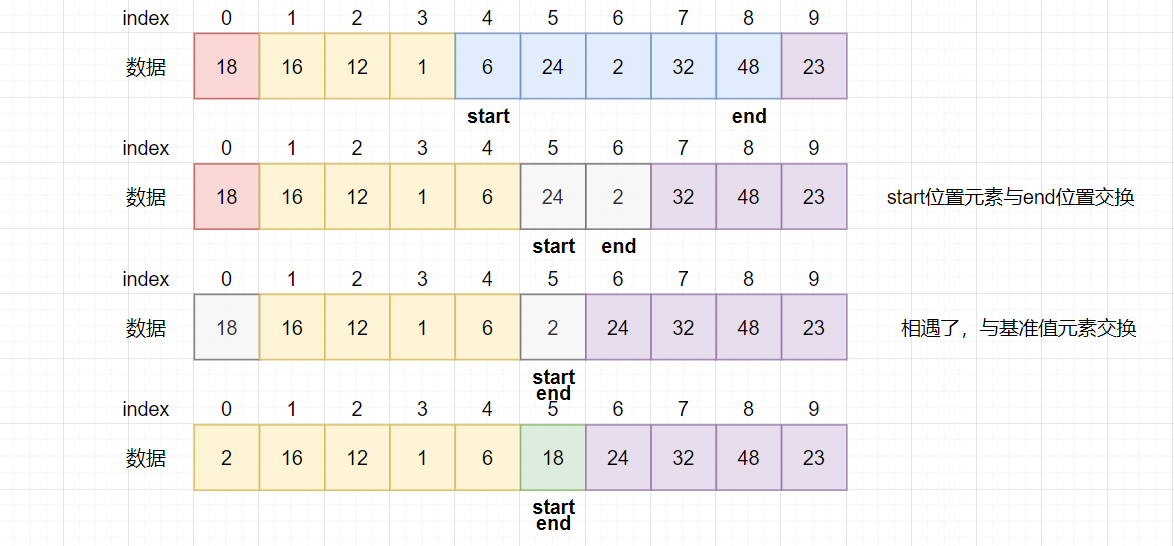
1. start从左边界开始向后遍历，遇到比基准值大的元素时停止，end从右边界开始向前遍历，遇到比基准值小的元素为止。
2. 然后交换这两个元素，start继续往后走，end继续往前走，start遇到比基准值大的元素，end遇到比基准值小的元素，交换。
3. 直到start与end相遇为止，将相遇位置（比基准值小的元素）与基准值原位置交换，此时基准值位置确定，左边元素小，右边元素大。
4. 分别对基准值左右序列进行上述相同的操作：取左边界元素为基准值，通过Hoare法确定基准值排序位置。直到左右序列只有一个元素或没有元素为止。

注意：先end遍历找比基准值小的元素，再start遍历找比基准值大的元素，这样最后相遇时的元素一定是比基准值小的元素。



Hoare 法实现代码：

//交换方法publicvoidswap(int[] arr,int index1,int index2){int tmp = arr[index1];
        arr[index1]= arr[index2];
        arr[index2]= tmp;}

/**
     * Hoare 法找基准
     * @param array 待排序数组对象
     * @param left 左边界
     * @param right 右边界
     * @return 基准值下标
     */publicinttest3(int[] array,int left,int right){int pivot = array[left];int start = left;int end = right;while(start < end){//从右边界开始找到比基准值小的元素，即遇到比基准值大的，end--while(start < end && array[end]>= pivot){
                end--;}//从左边界开始找到比基准值大的元素，即遇到比基准值小的，start++while(start < end && array[start]<= pivot){
                start++;}//交换这两个元素，将比基准值大的元素调整至右边，小的调整至左边swap(array, start, end);}//srart与end相遇,为基准值位置，将基准值与相遇出的元素交换swap(array,start, left);return start;}

实现Hoare 法的快速排序，只需将找基准的方法改为Hoare 法找基准的代码就可以了，其他都一样的。
基于Hoare 法快速排序动图：

基于Hoare 法快速排序代码：

/**
     * 快速排序
     * @param array 待排序数组对象
     */publicvoidquickSort(int[] array){quickSortFunc(array,0, array.length-1);}privatevoidquickSortFunc(int[] array,int start,int end){if(start >= end)return;//1.找基准int pivotIndex =findPivot(array, start, end);//2.快排基准左边元素序列quickSortFunc(array, start, pivotIndex-1);//3.快排基准右边元素序列quickSortFunc(array, pivotIndex+1, end);}/**
     * 找基准
     * @param array 待排序数组对象
     * @param left 左边界
     * @param right 右边界
     * @return 基准值下标
     */privateintfindPivot(int[] array,int left,int right){int pivot = array[left];int start = left;int end = right;while(start < end){//从右边界开始找到比基准值小的元素，即遇到比基准值大的，end--while(start < end && array[end]>= pivot){
                end--;}//从左边界开始找到比基准值大的元素，即遇到比基准值小的，start++while(start < end && array[start]<= pivot){
                start++;}//交换这两个元素，将比基准值大的元素调整至右边，小的调整至左边swap(array, start, end);}//srart与end相遇,为基准值位置，将基准值与相遇出的元素交换swap(array,start, left);return start;}

最后还有一个找基准的方法，就是前后遍历法，不详细说了，大概说一下思路吧！所谓前后遍历找基准就是将比基准值小的元素都放在基准值左边，然后将基准值与最右边比基准值小的元素交换，这样基准值就确定了位置，左边元素比它小，右边元素比它大。
实现代码：

/**
     * 前后遍历找基准
     * @param array 待排序数组对象
     * @param left 左边界
     * @param right 右边界
     * @return 基准值下标
     */publicinttest1(int[] array,int left,int right){int div = left +1;int pivot = array[left];for(int i = left +1; i <= right; i++){if(array[i]< pivot){swap(array, div, i);
                div++;}}swap(array, left, div -1);return div -1;}

2. 快速排序优化

2.1找基准值方案优化

假设数组长度为

n

，对于上述方法实现的快速排序过程其实类似二叉树的遍历，递归每层需要遍历数组元素的总个数为

    n
   
  
  
   n
  
 
n ，递归的高度为

 
  
   
    l
   
   
    o
   
   
    
     g
    
    
     2
    
   
   
    n
   
  
  
   log_2n
  
 
log2​n，所以快速排序时间复杂度为

 
  
   
    O
   
   
    (
   
   
    N
   
   
    l
   
   
    o
   
   
    g
   
   
    N
   
   
    )
   
  
  
   O(NlogN)
  
 
O(NlogN) ,空间复杂度为

 
  
   
    O
   
   
    (
   
   
    l
   
   
    o
   
   
    g
   
   
    N
   
   
    )
   
  
  
   O(logN)
  
 
O(logN)，但是这得是一棵完全二叉树逻辑结构的快排分组，由于我们直接选取第一个元素为基准值，这个基准值不一定是数组所有元素的中位数，甚至可能是最大或最小的元素，如果基准值是数组中最大或最小的元素，那么递归下来就是一棵单分支型的“树”，极端情况下，数组是有序或逆序情况下，每次找到的基准值都是最大或最小值，这时候时间复杂度为

 
  
   
    O
   
   
    (
   
   
    
     N
    
    
     2
    
   
   
    )
   
  
  
   O(N^2)
  
 
O(N2)，空间复杂度为

 
  
   
    O
   
   
    (
   
   
    N
   
   
    )
   
  
  
   O(N)
  
 
O(N)，所以我们需要对找基准值这一部分进行优化。

上面说过常见找基准值的方法有以下几种：

1. 取边界值法，即取目标序列最左边元素或最右边元素。
2. 随机值法，随机选取目标序列中的一个元素作为基准值。
3. 几个数取中法，常见三数取中间值。

前面实现快速排序找基准值我们使用的是直接取边界值法，使用这种方法当遇到有序或逆序的序列时，时间复杂度为

    O
   
   
    (
   
   
    
     N
    
    
     2
    
   
   
    )
   
  
  
   O(N^2)
  
 
O(N2)，空间复杂度为

 
  
   
    O
   
   
    (
   
   
    N
   
   
    )
   
  
  
   O(N)
  
 
O(N)，由于是递归，当有序或逆序的序列元素个数达到一定数量时就会造成栈溢出，为了解决这个问题，我们需要寻找其他找基准值方法。

优化方案1：随机取值法找基准值。使用该方法需要一定的运气，万一每次选取的基准值都是序列的最大或最小值，时间复杂度仍为

    O
   
   
    (
   
   
    
     N
    
    
     2
    
   
   
    )
   
  
  
   O(N^2)
  
 
O(N2)，空间复杂度仍为

 
  
   
    O
   
   
    (
   
   
    N
   
   
    )
   
  
  
   O(N)
  
 
O(N)，问题没有根本解决。

随机选取法找基准值动图演示（确定基准值的方法是前后遍历法）：
第一张动图第一次随机基准值为2，第二张动图第一次随机基准值为1（最小值），第三张动图第一次随机基准值为6。



由于使用随机找基准值不稳定，所以不是很推荐使用这种方案，只提供思路。

优化方案2： 三数取中间值法。在序列左右边界值，序列中点值三个数中选择一个居中的数字作为基准值。
我们不妨可以先判断左右边界值的大小，不妨设左边界下标为

left

右边界下标为

right

，中点下标为

mid

，数组为

array

。

右边界大：array[left] <= array[right]

情况1：array[mid] < array[left]
排列顺序：mid left right 取left。
情况2：array[mid] > array[right]
排列顺序：left right mid 取right。
其他情况排列顺序：left mid right 取mid。

左边界大：array[left] > array[right]

情况1：array[mid] > array[left]
排列顺序：right left mid 取left。
情况2：array[mid] < array[right]
排列顺序：mid right left 取right。
其他情况排列顺序：right mid left 取mid。

找基准方法优化版：

/**
     * 找基准 三数取中优化
     * @param array 待排序数组对象
     * @param left 左边界
     * @param right 右边界
     * @return 基准值下标
     */privateintfindPivotPlus(int[] array,int left,int right){int mid = left +((right - left)>>>1);//调整左边界元素为left  mid  right对应元素的中间大小值if(array[left]<= array[right]){//mid left rightif(array[mid]< array[left])swap(array, left, left);//left right midelseif(array[mid]> array[right])swap(array, left, right);//left mid rightelseswap(array, left, mid);}else{//right left midif(array[mid]> array[left])swap(array, left, left);//mid right leftelseif(array[mid]< array[right])swap(array, left, right);//right mid leftelseswap(array, left, mid);}int pivot = array[left];int start = left;int end = right;while(start < end){//从右边界end开始找比基准值小的元素while(start < end && array[end]>= pivot){
                end--;}//填上一个坑start，此时end位置挖坑
            array[start]= array[end];//从左边界start开始找比基准值大的元素while(start < end && array[start]<= pivot){
                start++;}//填上一个坑end，此时start位置挖坑
            array[end]= array[start];}//start与end相等时的位置，即基准值位置
        array[start]= pivot;return start;}

快速排序优化版：

/**
     * 快速排序优化
     * @param array 待排序数组
     */publicvoidquickSortPlus(int[] array){quickSortFuncPlus(array,0, array.length-1);}privatevoidquickSortFuncPlus(int[] array,int start,int end){if(start >= end)return;//1.找基准int pivotIndex =findPivotPlus(array, start, end);//2.快排基准左边元素序列quickSortFuncPlus(array, start, pivotIndex-1);//3.快排基准右边元素序列quickSortFuncPlus(array, pivotIndex+1, end);}

其他优化方案：

• 待排序区间小于一个阈值时（例如 100），使用其他排序方法（如插入排序）。
• 找基准 过程中把和基准值相等的数也选择出来

2.2非递归实现快速排序

非递归实现快速排序需要借助栈来实现，基本思路就是创建一个栈，初始放入待排序序列的左右边界（注意出栈顺序与入栈顺序相反），当栈不为空时分别取出右左边界，对该区间内的元素进行找基准，然后判断基准值左右序列是否有两个以上的元素，如果有将序列的左右边界下标入栈，待重新找基准确定元素位置。

非递归快速排序实现代码：

/**
     * 快速排序非递归实现
     * @param array 待排序数组
     */publicvoidquickSortIter(int[] array){Stack<Integer> stack =newStack<>();int left =0;int right = array.length -1;//分别将左右边界下标入栈，取出时，注意出栈顺序与入栈顺序相反
        stack.push(left);
        stack.push(right);while(!stack.isEmpty()){
            right = stack.pop();
            left = stack.pop();int pivotIndex =findPivotPlus(array, left, right);//基准左右序列的元素个数大于或等于两个则继续对左右序列找基准，确定位置，否则没必要再找基准if(pivotIndex > left +1){
                stack.push(left);
                stack.push(pivotIndex -1);}if(pivotIndex < right -1){
                stack.push(pivotIndex +1);
                stack.push(right);}}}/**
     * 找基准 三数取中优化
     * @param array 待排序数组对象
     * @param left 左边界
     * @param right 右边界
     * @return 基准值下标
     */privateintfindPivotPlus(int[] array,int left,int right){int mid = left +((right - left)>>>1);//调整左边界元素为left  mid  right对应元素的中间大小值if(array[left]<= array[right]){//mid left rightif(array[mid]< array[left])swap(array, left, left);//left right midelseif(array[mid]> array[right])swap(array, left, right);//left mid rightelseswap(array, left, mid);}else{//right left midif(array[mid]> array[left])swap(array, left, left);//mid right leftelseif(array[mid]< array[right])swap(array, left, right);//right mid leftelseswap(array, left, mid);}int pivot = array[left];int start = left;int end = right;while(start < end){//从右边界end开始找比基准值小的元素while(start < end && array[end]>= pivot){
                end--;}//填上一个坑start，此时end位置挖坑
            array[start]= array[end];//从左边界start开始找比基准值大的元素while(start < end && array[start]<= pivot){
                start++;}//填上一个坑end，此时start位置挖坑
            array[end]= array[start];}//start与end相等时的位置，即基准值位置
        array[start]= pivot;return start;}

3.快速排序性能分析

非优化版本：
时间复杂度空间复杂度稳定性最坏

       O
      
      
       (
      
      
       
        N
       
       
        2
       
      
      
       )
      
     
     
      O(N^{2} )
     
    
   O(N2)， 平均
   
    
     
      
       O
      
      
       (
      
      
       N
      
      
       l
      
      
       o
      
      
       g
      
      
       N
      
      
       )
      
     
     
      O(NlogN)
     
    
   O(NlogN)最坏
   
    
     
      
       O
      
      
       (
      
      
       N
      
      
       )
      
     
     
      O(N)
     
    
   O(N)， 平均
   
    
     
      
       O
      
      
       (
      
      
       l
      
      
       o
      
      
       g
      
      
       N
      
      
       )
      
     
     
      O(logN)
     
    
   O(logN)不稳定

三数取中间值法优化版：
时间复杂度空间复杂度稳定性

       O
      
      
       (
      
      
       N
      
      
       l
      
      
       o
      
      
       g
      
      
       N
      
      
       )
      
     
     
      O(NlogN)
     
    
   O(NlogN)
   
    
     
      
       O
      
      
       (
      
      
       l
      
      
       o
      
      
       g
      
      
       N
      
      
       )
      
     
     
      O(logN)
     
    
   O(logN)不稳定

好了，就分享到这里了，下期再见。

⭐️排序算法博文回放⭐️
时间博文名称链接2022.2.21排序算法之冒泡排序，选择排序，插入排序与希尔排序https://weijianhuawen.blog.csdn.net/article/details/122843122觉得文章写得不错的老铁们，点赞评论关注走一波！谢谢啦！