Pytorch优化器全总结（一）SGD、ASGD、Rprop、Adagrad

写在前面

    优化器时深度学习中的重要组件，在深度学习中有举足轻重的地位。在实际开发中我们并不用亲手实现一个优化器，很多框架都帮我们实现好了，但如果不明白各个优化器的特点，就很难选择适合自己任务的优化器。接下来我会开一个系列，以Pytorch为例，介绍所有主流的优化器，如果都搞明白了，对优化器算法的掌握也就差不多了。

    作为系列的第一篇文章，本文介绍Pytorch中的SGD、ASGD、Rprop、Adagrad，其中主要介绍SGD和Adagrad。因为这四个优化器出现的比较早，都存在一些硬伤，而作为现在主流优化器的基础又跳不过，所以作为开端吧。

    我们定义一个通用的思路框架，方便在后面理解各算法之间的关系和改进。首先定义待优化参数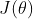 ![\theta](https://latex.codecogs.com/gif.latex?%5Ctheta)，目标函数![J(\theta )](https://latex.codecogs.com/gif.latex?J%28%5Ctheta%20%29)，学习率为 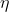![\eta](https://latex.codecogs.com/gif.latex?%5Ceta) ，然后我们进行迭代优化，假设当前的epoch为![t](https://latex.codecogs.com/gif.latex?t)，参数更新步骤如下：

计算目标函数关于当前参数的梯度：

$g_{t}=\bigtriangledown J(\theta _{t})$ （1）

根据历史梯度计算一阶动量和二阶动量：

$m_{t}=\phi (g_{1},g_{2}...,g_{t})$ （2）

$v_{t}=\varphi (g_{1},g_{2}...,g_{t})$ （3）

计算当前时刻的下降梯度：

$\bigtriangleup _{\theta _{t}}=\eta *\frac{m_{t}}{\sqrt{v_{t}}}$ （4）

根据下降梯度进行更新：

$\theta _{t+1}=\theta _{t}-\bigtriangleup _{\theta _{t}}$ （5）

    下面介绍的所有优化算法基本都能套用这个流程，只是式子（4）的形式会有变化。

一、 torch.optim.SGD 随机梯度下降

    该类可实现 SGD 优化算法，带动量 的SGD 优化算法和带 NAG(Nesterov accelerated gradient)的 SGD 优化算法,并且均可拥有 weight_decay（权重衰减） 项。

SGD代码

'''
params(iterable)- 参数组，优化器要优化的那部分参数。
lr(float)- 初始学习率，可按需随着训练过程不断调整学习率。
momentum(float)- 动量，通常设置为 0.9，0.8
dampening(float)- dampening for momentum ，暂时不了其功能，在源码中是这样用的：buf.mul_(momentum).add_(1 - dampening, d_p)，值得注意的是，若采用nesterov，dampening 必须为 0.
weight_decay(float)- 权值衰减系数，也就是 L2 正则项的系数
nesterov(bool)- bool 选项，是否使用 NAG(Nesterov accelerated gradient)
'''
class torch.optim.SGD(params, lr=<object object>, momentum=0, dampening=0, weight_decay=0, nesterov=False)

SGD算法解析

1.MBGD（Mini-batch Gradient Descent）小批量梯度下降法

    明明类名是SGD，为什么介绍MBGD呢，因为在Pytorch中，torch.optim.SGD其实是实现的MBGD，要想使用SGD，只要将batch_size设成1就行了。

    MBGD就是结合BGD和SGD的折中，对于含有 n个训练样本的数据集，每次参数更新，选择一个大小为 m(m<n) 的mini-batch数据样本计算其梯度，其参数更新公式如下,其中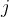![j](https://latex.codecogs.com/gif.latex?%5Cdpi%7B120%7D%20j)是一个batch的开始：

$\theta _{t+1}=\theta _{t}-\eta *\frac{1}{m}*\sum_{i=j}^{i=j+m-1}\bigtriangledown _{\theta _{i}}J_{i}(\theta _{t})$ （6）

优点：使用mini-batch的时候，可以收敛得很快，有一定摆脱局部最优的能力。

缺点：a.在随机选择梯度的同时会引入噪声，使得权值更新的方向不一定正确

       b.不能解决局部最优解的问题

2.Momentum动量

     动量是一种有助于在相关方向上加速SGD并抑制振荡的方法，**通过将当前梯度与过去梯度加权平均，来获取即将更新的梯度**。如下图b图所示。它通过将过去时间步长的更新向量的一小部分添加到当前更新向量来实现这一点：

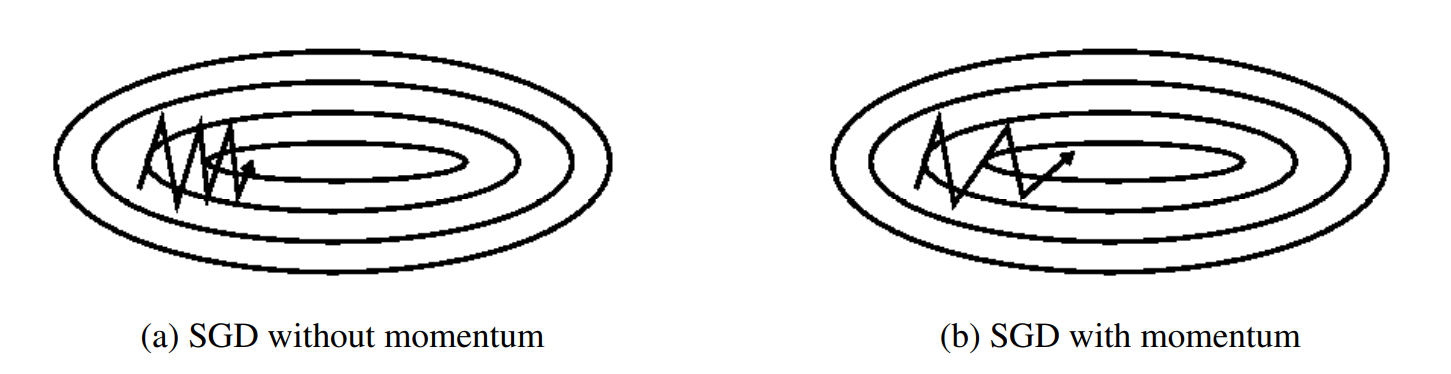
动量项通常设置为0.9或类似值。

参数更新公式如下，其中ρ 是动量衰减率，m是速率（即一阶动量）：

$g_{t}=\bigtriangledown_\theta J(\theta _{t})$ （7）

$m_{t} = \rho *m_{t-1} +g_{t}$ （8）

$\theta _{t+1}=\theta _{t}-\eta *m_{t}$ （9）

3.NAG(Nesterov accelerated gradient)

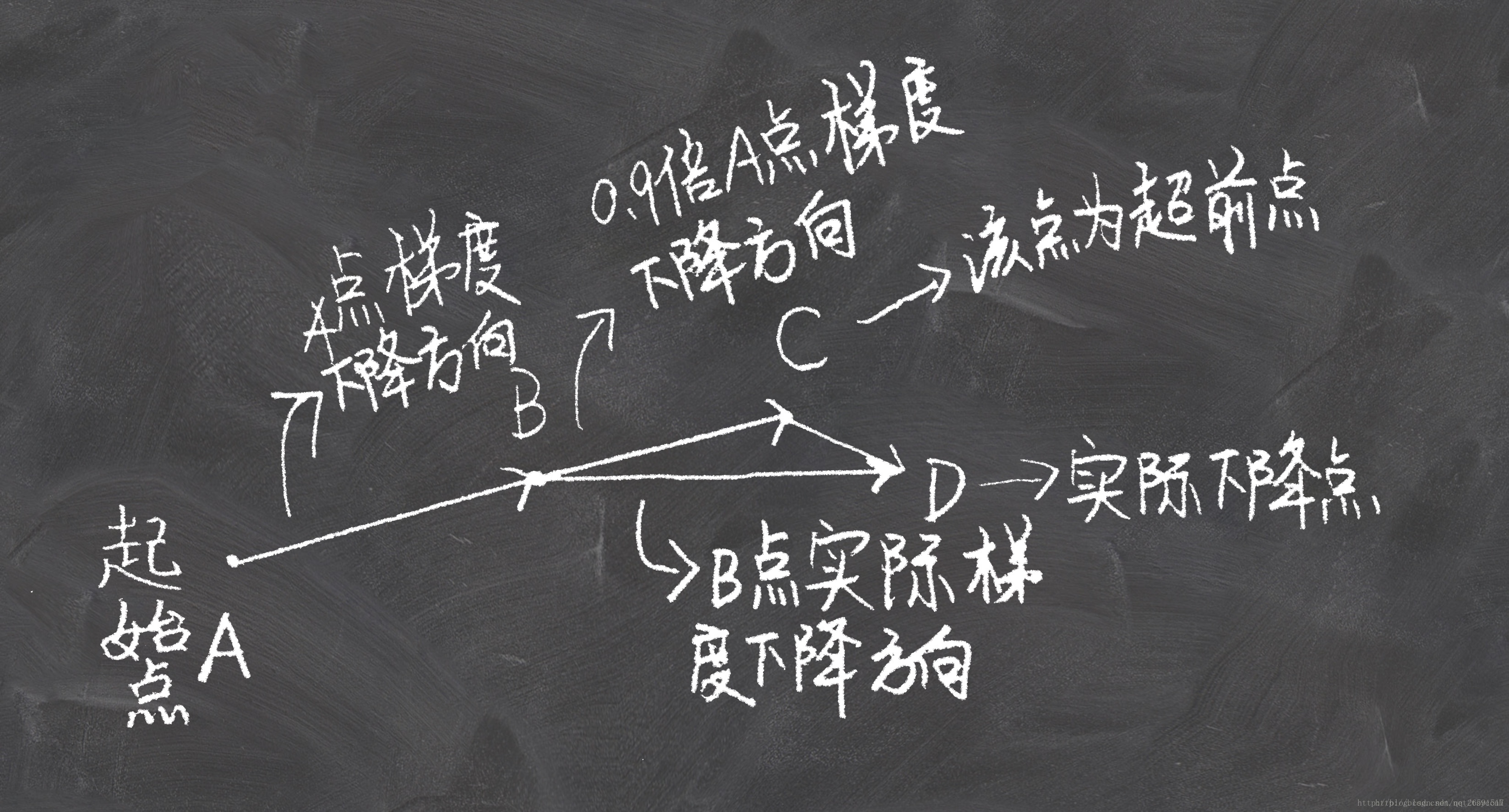
    NAG的思想是在动量法的基础上展开的。动量法是思想是，将当前梯度与过去梯度加权平均，来获取即将更新的梯度。在知道梯度之后，更新自变量到新的位置。也就是说我们其实在每一步，是知道下一时刻位置的。这时Nesterov就说了：那既然这样的话，我们何不**直接采用下一时刻的梯度来和上一时刻梯度进行加权平均**呢？下面两张图看明白，就理解NAG了：

    ![这里写图片描述](https://img-blog.csdn.net/20170728165011954?watermark/2/text/aHR0cDovL2Jsb2cuY3Nkbi5uZXQvdHN5Y2NuaA==/font/5a6L5L2T/fontsize/400/fill/I0JBQkFCMA==/dissolve/70/gravity/SouthEast)

NAG和经典动量法的差别就在B点和C点梯度的不同。

参数更新公式：

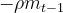$g_{t}=\bigtriangledown_\theta J(\theta _{t}-\rho m_{t-1})$ （10）

$m_{t} = \rho *m_{t-1} +g_{t}$ （11）

$\theta _{t+1}=\theta _{t}-\eta *m_{t}$ （12）

    上式中的![-\rho m_{t-1}](https://latex.codecogs.com/gif.latex?%5Cdpi%7B120%7D%20-%5Crho%20m_%7Bt-1%7D)就是图中的B到C那一段向量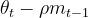，![\theta _{t}-\rho m_{t-1}](https://latex.codecogs.com/gif.latex?%5Cdpi%7B120%7D%20%5Ctheta%20_%7Bt%7D-%5Crho%20m_%7Bt-1%7D)就是C点坐标（参数）。可以看到NAG除了式子（10）与式子（7）有所不同，其余公式和Momentum是一样的。

    一般情况下NAG方法相比Momentum收敛速度快、波动也小。实际上NAG方法用到了二阶信息，所以才会有这么好的结果。

     Nesterov动量梯度的计算在模型参数施加当前速度之后，因此可以理解为往标准动量中添加了一个校正因子。在凸批量梯度的情况下，Nesterov动量将额外误差收敛率从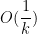![O(\frac{1}{k})](https://latex.codecogs.com/gif.latex?%5Cdpi%7B100%7D%20O%28%5Cfrac%7B1%7D%7Bk%7D%29)(k步后)改进到 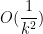 ![O(\frac{1}{k^2})](https://latex.codecogs.com/gif.latex?%5Cdpi%7B100%7D%20O%28%5Cfrac%7B1%7D%7Bk%5E2%7D%29)，然而，在随机梯度情况下，Nesterov动量对收敛率的作用却不是很大。

SGD总结

使用了Momentum或NAG的MBGD有如下特点：

优点：加快收敛速度，有一定摆脱局部最优的能力，一定程度上缓解了没有动量的时候的问题

缺点：a.仍然继承了一部分SGD的缺点

** **b.在随机梯度情况下，NAG对收敛率的作用不是很大

      c.Momentum和NAG都是为了使梯度更新更灵活。但是人工设计的学习率总是有些生硬，下面介绍几种自适应学习率的方法。

推荐程度：带Momentum的torch.optim.SGD 可以一试。

二、torch.optim.ASGD随机平均梯度下降

    ASGD 也称为 SAG，表示随机平均梯度下降(Averaged Stochastic Gradient Descent)，简单地说 ASGD 就是用空间换时间的一种 SGD，因为很少使用，所以不详细介绍，详情可参看论文： http://riejohnson.com/rie/stograd_nips.pdf

'''
params(iterable)- 参数组,优化器要优化的那些参数。
lr(float)- 初始学习率，可按需随着训练过程不断调整学习率。
lambd(float)- 衰减项，默认值 1e-4。
alpha(float)- power for eta update ，默认值 0.75。
t0(float)- point at which to start averaging，默认值 1e6。
weight_decay(float)- 权值衰减系数，也就是 L2 正则项的系数。
'''
class torch.optim.ASGD(params, lr=0.01, lambd=0.0001, alpha=0.75, t0=1000000.0, weight_decay=0)

推荐程度：不常见

三、torch.optim.Rprop

    该类实现 Rprop 优化方法(弹性反向传播)，适用于 full-batch，不适用于 mini-batch，因而在 mini-batch 大行其道的时代里，很少见到。

'''
params - 参数组,优化器要优化的那些参数。
lr - 学习率
etas (Tuple[float, float])- 乘法增减因子
step_sizes (Tuple[float, float]) - 允许的最小和最大步长
'''
class torch.optim.Rprop(params, lr=0.01, etas=(0.5, 1.2), step_sizes=(1e-06, 50))

优点：它可以自动调节学习率，不需要人为调节

缺点：仍依赖于人工设置一个全局学习率,随着迭代次数增多，学习率会越来越小，最终会趋近于0

推荐程度：不推荐

四、torch.optim.Adagrad 自适应梯度

    该类可实现 Adagrad 优化方法(Adaptive Gradient)，Adagrad 是一种自适应优化方法，是自适应的为各个参数分配不同的学习率。这个学习率的变化，会受到梯度的大小和迭代次数的影响。梯度越大，学习率越小；梯度越小，学习率越大。

Adagrad 代码

'''
params (iterable) – 待优化参数的iterable或者是定义了参数组的dict
lr (float, 可选) – 学习率（默认: 1e-2）
lr_decay (float, 可选) – 学习率衰减（默认: 0）
weight_decay (float, 可选) – 权重衰减（L2惩罚）（默认: 0）
initial_accumulator_value - 累加器的起始值，必须为正。

'''
class torch.optim.Adagrad(params, lr=0.01, lr_decay=0, weight_decay=0, initial_accumulator_value=0)

Adagrad 算法解析

    AdaGrad对学习率进行了一个约束，对于经常更新的参数，我们已经积累了大量关于它的知识，不希望被单个样本影响太大，希望学习速率慢一些；对于偶尔更新的参数，我们了解的信息太少，希望能从每个偶然出现的样本身上多学一些，即学习速率大一些。这样大大提高梯度下降的鲁棒性**。**而该方法中开始使用二阶动量，才意味着“自适应学习率”优化算法时代的到来。
     在SGD中，我们每次迭代对所有参数进行更新，因为每个参数使用相同的学习率。而AdaGrad在每个时间步长对每个参数使用不同的学习率。AdaGrad消除了手动调整学习率的需要。AdaGrad在迭代过程中不断调整学习率，并让目标函数中的每个参数都分别拥有自己的学习率。大多数实现使用学习率默认值为0.01，开始设置一个较大的学习率。

    AdaGrad引入了二阶动量。二阶动量是迄今为止所有梯度值的平方和，即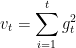![v_{t}=\sum_{i=1}^{t}g_{t}^{2}](https://latex.codecogs.com/gif.latex?%5Cdpi%7B100%7D%20v_%7Bt%7D%3D%5Csum_%7Bi%3D1%7D%5E%7Bt%7Dg_%7Bt%7D%5E%7B2%7D)它是用来度量历史更新频率的。也就是说，我们的学习率现在是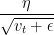![\frac{\eta }{\sqrt{v_{t}+\epsilon }}](https://latex.codecogs.com/gif.latex?%5Cdpi%7B100%7D%20%5Cfrac%7B%5Ceta%20%7D%7B%5Csqrt%7Bv_%7Bt%7D&amp;plus;%5Cepsilon%20%7D%7D)，从这里我们就会发现 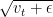![\sqrt{v_{t}+\epsilon }](https://latex.codecogs.com/gif.latex?%5Cdpi%7B100%7D%20%5Csqrt%7Bv_%7Bt%7D&amp;plus;%5Cepsilon%20%7D)是恒大于0的，而且参数更新越频繁，二阶动量越大，学习率就越小，这一方法在稀疏数据场景下表现非常好，参数更新公式如下： 

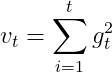    ![v_{t}=\sum_{i=1}^{t}g_{t}^{2}](https://latex.codecogs.com/gif.latex?%5Cdpi%7B150%7D%20v_%7Bt%7D%3D%5Csum_%7Bi%3D1%7D%5E%7Bt%7Dg_%7Bt%7D%5E%7B2%7D)                                                    （13）

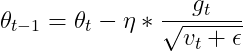    ![\theta _{t-1}=\theta _{t}-\eta *\frac{g_{t}}{\sqrt{v_{t}+\epsilon }}](https://latex.codecogs.com/gif.latex?%5Cdpi%7B150%7D%20%5Ctheta%20_%7Bt-1%7D%3D%5Ctheta%20_%7Bt%7D-%5Ceta%20*%5Cfrac%7Bg_%7Bt%7D%7D%7B%5Csqrt%7Bv_%7Bt%7D&amp;plus;%5Cepsilon%20%7D%7D)                        （14）

AdaGrad总结

** AdaGrad在每个时间步长对每个参数使用不同的学习率。并且引入了二阶动量，二阶动量是迄今为止所有梯度值的平方和。**

优点：AdaGrad消除了手动调整学习率的需要。AdaGrad在迭代过程中不断调整学习率，并让目标函数中的每个参数都分别拥有自己的学习率。

缺点：a.仍需要手工设置一个全局学习率 , 如果设置过大的话，会使regularizer过于敏感，对梯度的调节太大

    b.在分母中累积平方梯度，由于每个添加项都是正数，因此在训练过程中累积和不断增长。这导致学习率不断变小并最终变得无限小，此时算法不再能够获得额外的知识即导致模型不会再次学习。