扩散模型可以看作是一个层次很深的VAE(变分自编码器),前向(forward,或者译为正向)的过程,通过在多个尺度上添加噪声来逐步扰乱数据分布;然后是反向的过程,去学习如何恢复数据结构,上述的破坏和恢复过程分别对应于VAE中的编码和解码过程。所以VAE是一个重要的概念需要掌握,本文将用python从头开始实现VAE和CVAE,来增加对于它们的理解。
什么是自编码器?它们的作用是什么
自编码器是一种由编码器和解码器两部分组成的神经系统结构。解码器在编码器之后,中间是所谓的隐藏层,它有各种各样的名称,有时可以称为瓶颈层、潜在空间、隐藏层、编码层或编码层。它看起来像这样:
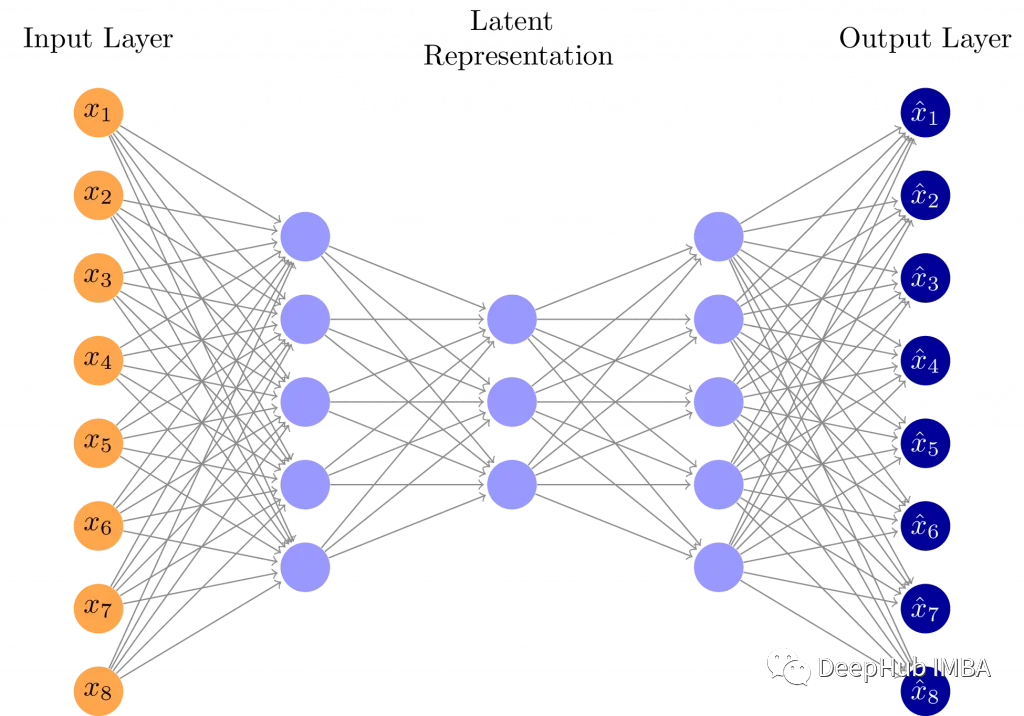
自编码器可以应用在各种用途上。最常见的就是数据压缩:当输入信号通过编码器部分时,图像的潜在表示在尺寸上要小得多。例如,在上图中,虽然输入信号用8个值表示,但其压缩表示只需要3个值。
自编码器也可以用于各种其他目的:数据去噪,特征学习,异常检测,以及现在大火的稳定扩散模型。
自编码器的实现
我们将使用MNIST数据集。要将MNIST下载到本地文件夹,请运行以下命令:
# Download the files
url = "http://yann.lecun.com/exdb/mnist/"
filenames = ['train-images-idx3-ubyte.gz', 'train-labels-idx1-ubyte.gz',
't10k-images-idx3-ubyte.gz', 't10k-labels-idx1-ubyte.gz']
data = []
for filename in filenames:
print("Downloading", filename)
request.urlretrieve(url + filename, filename)
with gzip.open(filename, 'rb') as f:
if 'labels' in filename:
# Load the labels as a one-dimensional array of integers
data.append(np.frombuffer(f.read(), np.uint8, offset=8))
else:
# Load the images as a two-dimensional array of pixels
data.append(np.frombuffer(f.read(), np.uint8, offset=16).reshape(-1,28*28))
# Split into training and testing sets
X_train, y_train, X_test, y_test = data
# Normalize the pixel values
X_train = X_train.astype(np.float32) / 255.0
X_test = X_test.astype(np.float32) / 255.0
# Convert labels to integers
y_train = y_train.astype(np.int64)
y_test = y_test.astype(np.int64)
现在我们有了训练和测试集,首先让我们看看图像:
def show_images(images, labels):
"""
Display a set of images and their labels using matplotlib.
The first column of `images` should contain the image indices,
and the second column should contain the flattened image pixels
reshaped into 28x28 arrays.
"""
# Extract the image indices and reshaped pixels
pixels = images.reshape(-1, 28, 28)
# Create a figure with subplots for each image
fig, axs = plt.subplots(
ncols=len(images), nrows=1, figsize=(10, 3 * len(images))
)
# Loop over the images and display them with their labels
for i in range(len(images)):
# Display the image and its label
axs[i].imshow(pixels[i], cmap="gray")
axs[i].set_title("Label: {}".format(labels[i]))
# Remove the tick marks and axis labels
axs[i].set_xticks([])
axs[i].set_yticks([])
axs[i].set_xlabel("Index: {}".format(i))
# Adjust the spacing between subplots
fig.subplots_adjust(hspace=0.5)
# Show the figure
plt.show()
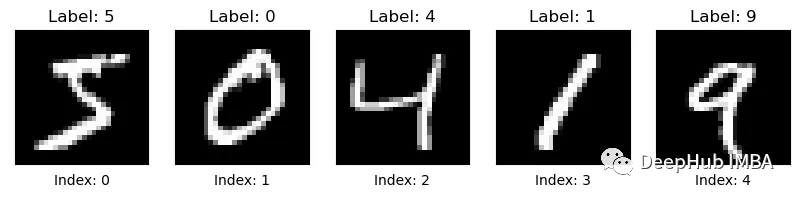
因为数据比较简单,所以我们这里直接使用线性层,这样方便我们进行计算:
import torch.nn as nn
class AutoEncoder(nn.Module):
def __init__(self):
super().__init__()
# Set the number of hidden units
self.num_hidden = 8
# Define the encoder part of the autoencoder
self.encoder = nn.Sequential(
nn.Linear(784, 256), # input size: 784, output size: 256
nn.ReLU(), # apply the ReLU activation function
nn.Linear(256, self.num_hidden), # input size: 256, output size: num_hidden
nn.ReLU(), # apply the ReLU activation function
)
# Define the decoder part of the autoencoder
self.decoder = nn.Sequential(
nn.Linear(self.num_hidden, 256), # input size: num_hidden, output size: 256
nn.ReLU(), # apply the ReLU activation function
nn.Linear(256, 784), # input size: 256, output size: 784
nn.Sigmoid(), # apply the sigmoid activation function to compress the output to a range of (0, 1)
)
def forward(self, x):
# Pass the input through the encoder
encoded = self.encoder(x)
# Pass the encoded representation through the decoder
decoded = self.decoder(encoded)
# Return both the encoded representation and the reconstructed output
return encoded, decoded
训练时我们并不需要图像标签,因为我这是一种无监督的方法。这里我们选择使用简单的均方误差损失,因为我们想以最精确的方式重建我们的图像。让我们做一些准备工作:
# Convert the training data to PyTorch tensors
X_train = torch.from_numpy(X_train)
# Create the autoencoder model and optimizer
model = AutoEncoder()
optimizer = optim.Adam(model.parameters(), lr=learning_rate)
# Define the loss function
criterion = nn.MSELoss()
# Set the device to GPU if available, otherwise use CPU
model.to(device)
# Create a DataLoader to handle batching of the training data
train_loader = torch.utils.data.DataLoader(
X_train, batch_size=batch_size, shuffle=True
)
最后,训练循环也很标准:
# Training loop
for epoch in range(num_epochs):
total_loss = 0.0
for batch_idx, data in enumerate(train_loader):
# Get a batch of training data and move it to the device
data = data.to(device)
# Forward pass
encoded, decoded = model(data)
# Compute the loss and perform backpropagation
loss = criterion(decoded, data)
optimizer.zero_grad()
loss.backward()
optimizer.step()
# Update the running loss
total_loss += loss.item() * data.size(0)
# Print the epoch loss
epoch_loss = total_loss / len(train_loader.dataset)
print(
"Epoch {}/{}: loss={:.4f}".format(epoch + 1, num_epochs, epoch_loss)
)
为了计算损失,将输入图像与重建后的图像直接进行进行比较就可以了。训练速度会很快,甚至你可以在CPU上完成。当训练完成后,比较输出和输入图像:
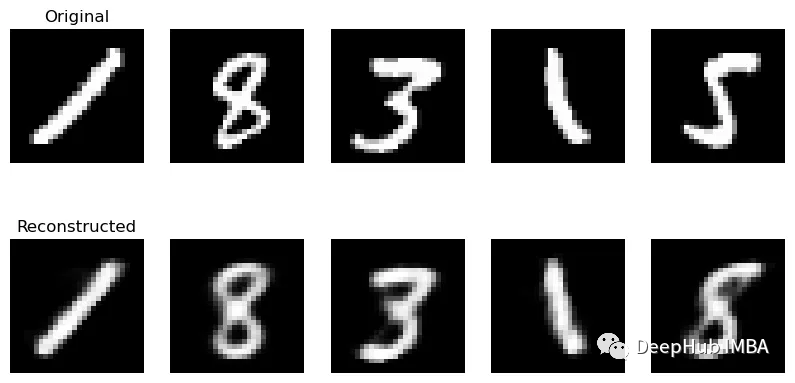
上面一行是原始图像,下面一行是重建图像。
这里有几个问题:
1、重建的图像很模糊。这是因为重建并不完美。
2、这种类型的压缩不是免费的,它是以在解码过程中会出现问题,3、我们只使用8个隐藏单元,增加隐藏单元的数量会提高图像质量,而减少它们会使模糊更严重。
看看32个隐藏单元的结果:
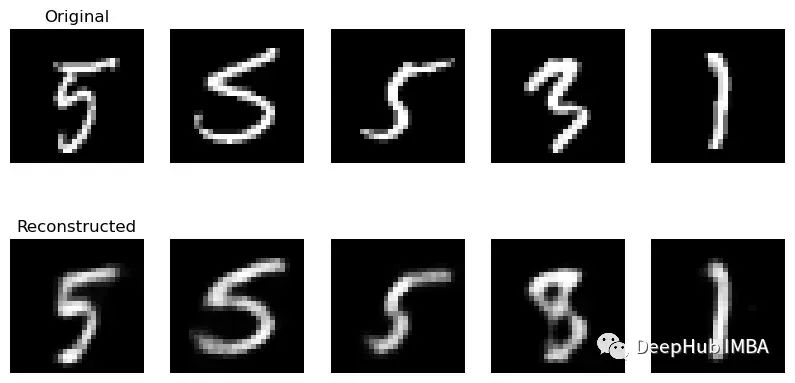
自编码器对于现有数据表现得还不错,但是他有一个最大的问题,就是生成新数据非常困难。如果我们去掉编码器部分,只从潜在层开始,我们应该能够得到一个有意义的图像。但是对于自编码器来说,没有方法可以有意义的方式对潜在空间进行采样,即提出一种可靠的采样策略,以确保输出图像是可读的,并且还会发生一定的变化。
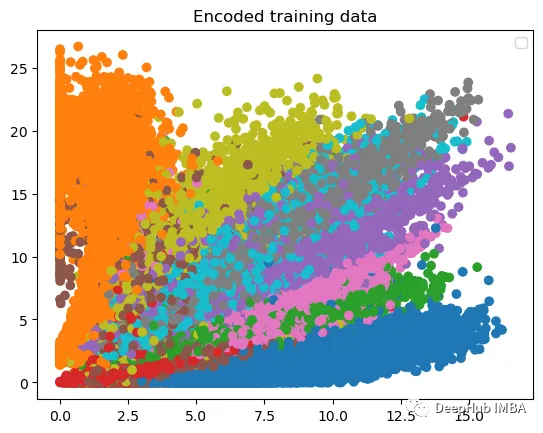
现在我们要做的是从这个潜在空间生成一堆样本。从这个潜在空间分布中生成样本有点困难,所以我们从矩形中生成样本。这是我们得到的结果:

虽然有些样本看起来很好,但要对同一空间进行有意义的采样将会变得更加困难,因为该空间的维数更高。例如,如果我们将维度增加到32,结果如下:

数字已经无法辨认了,哪有没有更好的办法呢?
变分自编码器 VAE
变分自编码器(VAEs)的论文名为“Auto-Encoding Variational Bayes”,由Diederik P. Kingma和Max Welling于2014年发表。
VAEs为我们提供了一种更灵活的方法来学习领域的潜在表示。基本思想很简单:我们学习的是潜在空间分布的参数,而不是具体的数值。而生成潜在变量时不是直接从潜在表示中获取,而是使用潜在空间分布参数来生成潜在表示。
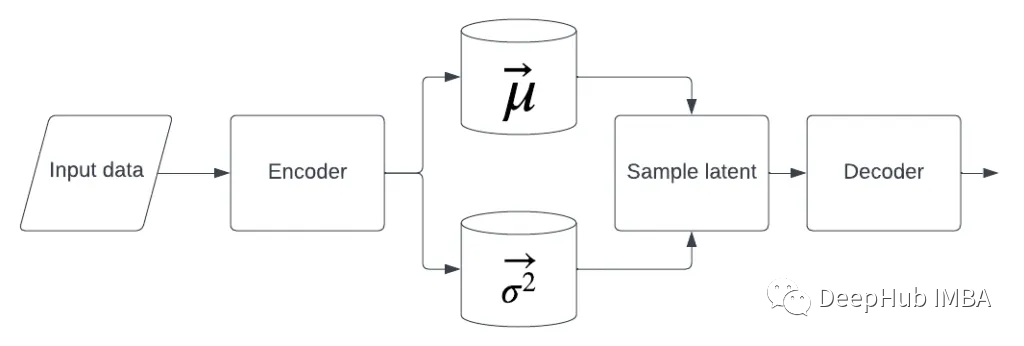
我们使用输入数据学习均值和方差的向量,便稍后使用它们对将要用解码器解码的潜在变量进行采样
但是采样操作是不可微的。所以使用了一种叫做重新参数化的技巧。它的工作原理是这样的:我们不再从那个块中获取样本,而是明确地学习均值和方差的两个向量,然后有一个独立的块,只从中采样

因此,我们不直接对这些分布进行抽样,而是做以下操作:
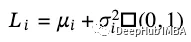
𝐿~表示潜在表示的一个组成部分。所以现在的模型变成了这样
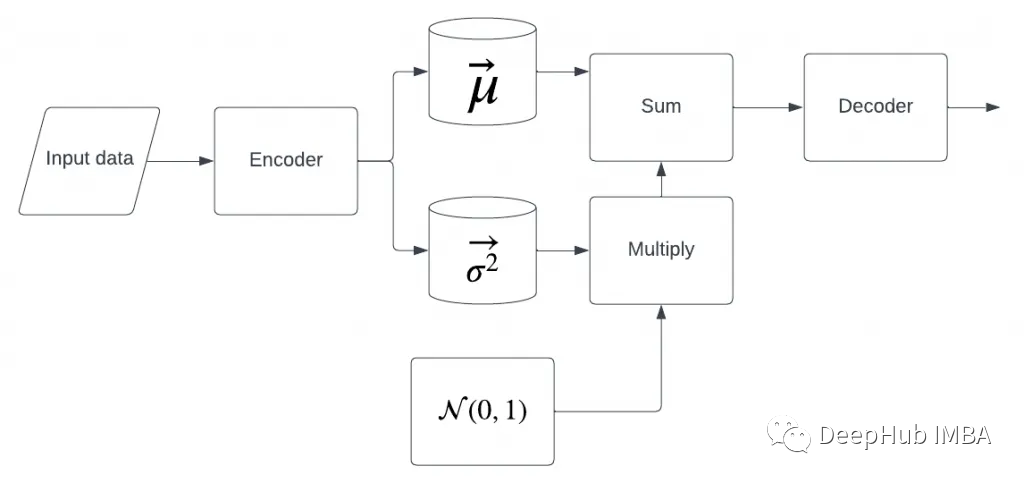
上面的模型代码也随之改变:
class VAE(AutoEncoder):
def __init__(self):
super().__init__()
# Add mu and log_var layers for reparameterization
self.mu = nn.Linear(self.num_hidden, self.num_hidden)
self.log_var = nn.Linear(self.num_hidden, self.num_hidden)
def reparameterize(self, mu, log_var):
# Compute the standard deviation from the log variance
std = torch.exp(0.5 * log_var)
# Generate random noise using the same shape as std
eps = torch.randn_like(std)
# Return the reparameterized sample
return mu + eps * std
def forward(self, x):
# Pass the input through the encoder
encoded = self.encoder(x)
# Compute the mean and log variance vectors
mu = self.mu(encoded)
log_var = self.log_var(encoded)
# Reparameterize the latent variable
z = self.reparameterize(mu, log_var)
# Pass the latent variable through the decoder
decoded = self.decoder(z)
# Return the encoded output, decoded output, mean, and log variance
return encoded, decoded, mu, log_var
def sample(self, num_samples):
with torch.no_grad():
# Generate random noise
z = torch.randn(num_samples, self.num_hidden).to(device)
# Pass the noise through the decoder to generate samples
samples = self.decoder(z)
# Return the generated samples
return samples
我们如何训练这模型呢?首先来定义损失函数:
# Define a loss function that combines binary cross-entropy and Kullback-Leibler divergence
def loss_function(recon_x, x, mu, logvar):
# Compute the binary cross-entropy loss between the reconstructed output and the input data
BCE = F.binary_cross_entropy(recon_x, x.view(-1, 784), reduction="sum")
# Compute the Kullback-Leibler divergence between the learned latent variable distribution and a standard Gaussian distribution
KLD = -0.5 * torch.sum(1 + logvar - mu.pow(2) - logvar.exp())
# Combine the two losses by adding them together and return the result
return BCE + KLD
第一个分量我们已经很熟悉了,它只是重构误差。第二个部分引入了对学习分布偏离先验分布过多的惩罚,还记得我们所过几次的KL散度,他可以比较两个概率分布之间的相似性,我们比较的是我们的分布与标准正态分布的相似性,有了这个函数,我们就可以这样训练:
def train_vae(X_train, learning_rate=1e-3, num_epochs=10, batch_size=32):
# Convert the training data to PyTorch tensors
X_train = torch.from_numpy(X_train).to(device)
# Create the autoencoder model and optimizer
model = VAE()
optimizer = optim.Adam(model.parameters(), lr=learning_rate)
# Define the loss function
criterion = nn.MSELoss(reduction="sum")
# Set the device to GPU if available, otherwise use CPU
model.to(device)
# Create a DataLoader to handle batching of the training data
train_loader = torch.utils.data.DataLoader(
X_train, batch_size=batch_size, shuffle=True
)
# Training loop
for epoch in range(num_epochs):
total_loss = 0.0
for batch_idx, data in enumerate(train_loader):
# Get a batch of training data and move it to the device
data = data.to(device)
# Forward pass
encoded, decoded, mu, log_var = model(data)
# Compute the loss and perform backpropagation
KLD = -0.5 * torch.sum(1 + log_var - mu.pow(2) - log_var.exp())
loss = criterion(decoded, data) + 3 * KLD
optimizer.zero_grad()
loss.backward()
optimizer.step()
# Update the running loss
total_loss += loss.item() * data.size(0)
# Print the epoch loss
epoch_loss = total_loss / len(train_loader.dataset)
print(
"Epoch {}/{}: loss={:.4f}".format(epoch + 1, num_epochs, epoch_loss)
)
# Return the trained model
return model
下面看看我们生成的图像:

图像看起来还是很模糊,这是因为我们使用MAE来进行重建控制,使用其他的损失会好
最后一件非常有趣的事情是生成一个随机向量,然后逐渐改变它的一个维度,同时保持其他维度固定。这样我们就可以看到解码器的输出是如何变化的。下面是一些例子:

通过改变它的一个分量我们从0移动到9,然后移动到1或7。
生成具有特定标签的图像 CVAE
为了生成具有特定标签的图像,编码器需要学习如何在给定提示时解码潜在变量。在这种情况下,我们用一些信息来限制编码器,怎么能做到呢?一个很明显的想法是将一个编码数字标签传递给解码器,这样它就可以学习解码过程。它看起来像这样:
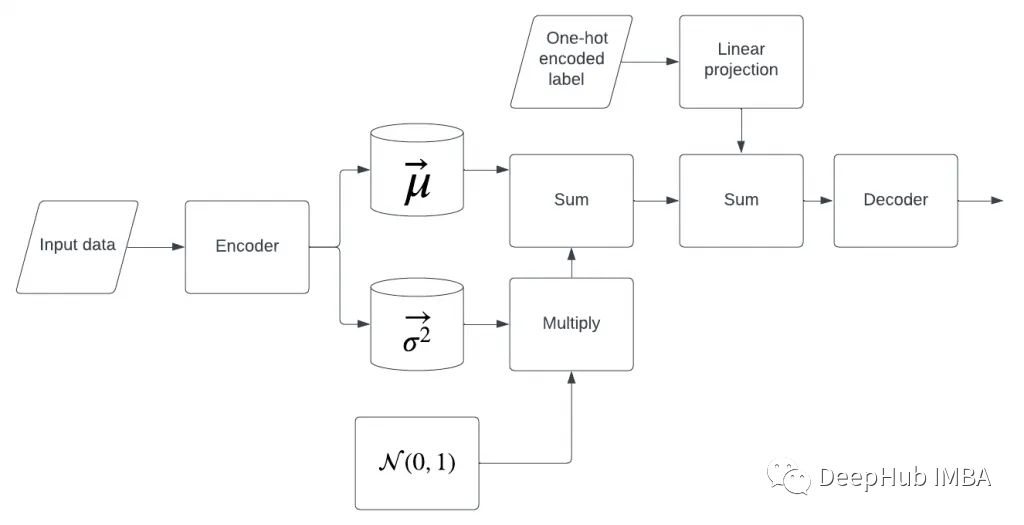
现在为解码器增加了一个额外的信息源。为什么我们先做线性投影再求和?线性投影是指有匹配的码层尺寸和标签信息,我们需要将他投影到与潜在空间相同的维度,然后把它们加起来。也可以取平均值,或者逐点乘法,或者只是把这些向量连接起来——任何类似的方法都可以,我们这里只是简单的相加。看看这个图,是不是和扩散模型有点像了(cvae可是2016年发布的)。
然后在推理时,我们要做的就是传递一个想要生成的数字的标签。代码就变为了:
class ConditionalVAE(VAE):
# VAE implementation from the article linked above
def __init__(self, num_classes):
super().__init__()
# Add a linear layer for the class label
self.label_projector = nn.Sequential(
nn.Linear(num_classes, self.num_hidden),
nn.ReLU(),
)
def condition_on_label(self, z, y):
projected_label = self.label_projector(y.float())
return z + projected_label
def forward(self, x, y):
# Pass the input through the encoder
encoded = self.encoder(x)
# Compute the mean and log variance vectors
mu = self.mu(encoded)
log_var = self.log_var(encoded)
# Reparameterize the latent variable
z = self.reparameterize(mu, log_var)
# Pass the latent variable through the decoder
decoded = self.decoder(self.condition_on_label(z, y))
# Return the encoded output, decoded output, mean, and log variance
return encoded, decoded, mu, log_var
def sample(self, num_samples, y):
with torch.no_grad():
# Generate random noise
z = torch.randn(num_samples, self.num_hidden).to(device)
# Pass the noise through the decoder to generate samples
samples = self.decoder(self.condition_on_label(z, y))
# Return the generated samples
return samples
这里有一个叫做label_projector的新层,它做线性投影。潜在空间在前向传递和采样过程中都通过该层。
CVAE损失还是VAE的损失,训练也基本一样,我们这里就只看结果了:
num_samples = 10
random_labels = [8] * num_samples
show_images(
cvae.sample(num_samples, one_hot(torch.LongTensor(random_labels), num_classes=10).to(device))
.cpu()
.detach()
.numpy(),
labels=random_labels,
)

可以看到,我们的图像基本固定了,并不会出现其他数字
总结
自编码器是理解无监督学习和数据压缩的基础。虽然简单的自动编码器可以重建图像,但它们难以生成新数据。变分自编码器(VAEs)提供了一种更灵活的方法,通过学习可采样的潜在空间分布的参数来生成新数据。利用重参数化技巧使采样操作可微。而CVAE又为后来的提供了条件支持,所以学习这些会对我们理解稳定扩散模型提供很好的理论基础。
作者 Konstantin Sofeikov