机器学习（线性回归实训）------波士顿房价

1.机器学习

机器学习是人工智能 (AI) 和计算机科学的分支，专注于使用数据和算法来模仿人类学习的方式，逐渐提高其准确性。机器学习是不断成长的数据科学领域的重要组成部分。 通过使用统计方法，对算法进行训练，以进行分类或预测，揭示数据挖掘项目中的关键洞察。 然后，这些洞察可推动应用和业务中的决策，有效影响关键增长指标。 随着大数据的持续扩大和增长，数据科学家的市场需求也水涨船高，要求他们协助确定最相关的业务问题，并随后提供数据以获得答案。

2.机器学习如何运作？

三个主要部分：决策过程，误差函数，模型优化过程

1. **决策过程： **通常，机器学习算法用于进行预测或分类。 算法可根据一些标签化或未标签化的输入数据，生成有关数据中模式的估算。
2. **误差函数： **误差函数用于评估模型的预测。 如果存在已知示例，那么误差函数可以进行比较以评估模型的准确性。
3. **模型优化过程： **如果模型能够更好地拟合训练集中的数据点，那么会调整权重以减少已知示例和模型估算之间的差异。 该算法将重复此评估并优化过程，自主更新权重，直到满足精确性阈值为止。

3.线性回归

回归分析是用来评估变量之间关系的统计过程。用来解释自变量X与因变量Y的关系。即当自变量X发生改变时，因变量Y会如何发生改变。
线性回归是回归分析的一种，评估的自变量X与因变量Y之间是一种线性关系。当只有一个自变量时，称为简单线性回归，当具有多个自变量时，称为多元线性回归。在线性回归中，数据使用线性预测函数来建模，并且未知的模型参数也是通过数据来估计。

4.波士顿房价----多元线性回归程序

4.1.1 安装sklearn镜像

4.1.2 导入各种库和包

4.1.3 获取各种所需要的数据

4.1.4 导出横坐标的数据x

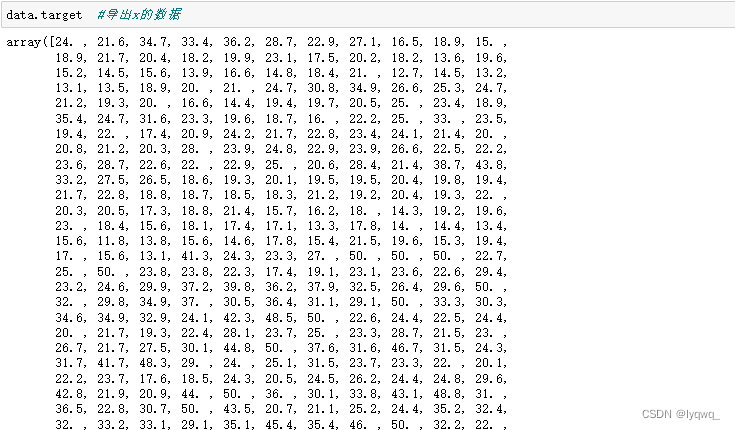
4.1.5 导出纵坐标的数据y

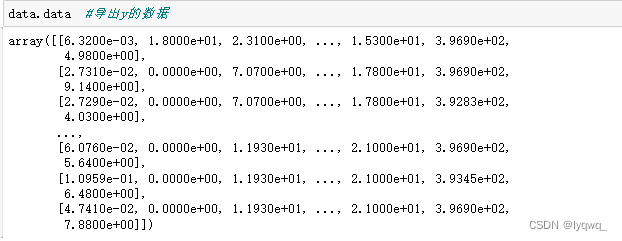
4.1.6 线性回归方程 完成机器学习六个步骤 1.导入数据 2.清洗数据 3.特征工程（提取有价值的数据）4.建模 5.评估 6.可视化（画图）

4.1.7 调用函数

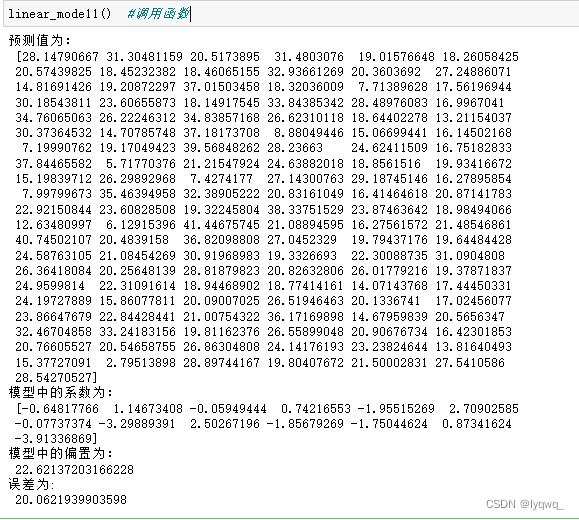
5.最后完整代码及运行结果如下：

pip install -i https://pypi.tuna.tsinghua.edu.cn/simple/ sklearn #安装镜像

Looking in indexes: https://pypi.tuna.tsinghua.edu.cn/simple/Note: you may need to restart the kernel to use updated packages.

Requirement already satisfied: sklearn in d:\anaconda\lib\site-packages (0.0.post1)

from sklearn.datasets import load_boston #导入sklearn工具库，获取数据
from sklearn.model_selection import train_test_split #导入sklearn工具库，数据处理
from sklearn.preprocessing import StandardScaler #导入sklearn工具库，切分数据
from sklearn.linear_model import LinearRegression #导入线性回归算法模型，特征工程——标准化
from sklearn.metrics import mean_squared_error #导入sklearn工具库，模型评估
import pandas as pd #导入pandas库
import numpy as np #导入numpy库，均方误差

data=load_boston()
data.keys() #获取页面中需要的数据

dict_keys(['data', 'target', 'feature_names', 'DESCR', 'filename', 'data_module'])

data.target #导出x的数据

array([24. , 21.6, 34.7, 33.4, 36.2, 28.7, 22.9, 27.1, 16.5, 18.9, 15. ,
       18.9, 21.7, 20.4, 18.2, 19.9, 23.1, 17.5, 20.2, 18.2, 13.6, 19.6,
       15.2, 14.5, 15.6, 13.9, 16.6, 14.8, 18.4, 21. , 12.7, 14.5, 13.2,
       13.1, 13.5, 18.9, 20. , 21. , 24.7, 30.8, 34.9, 26.6, 25.3, 24.7,
       21.2, 19.3, 20. , 16.6, 14.4, 19.4, 19.7, 20.5, 25. , 23.4, 18.9,
       35.4, 24.7, 31.6, 23.3, 19.6, 18.7, 16. , 22.2, 25. , 33. , 23.5,
       19.4, 22. , 17.4, 20.9, 24.2, 21.7, 22.8, 23.4, 24.1, 21.4, 20. ,
       20.8, 21.2, 20.3, 28. , 23.9, 24.8, 22.9, 23.9, 26.6, 22.5, 22.2,
       23.6, 28.7, 22.6, 22. , 22.9, 25. , 20.6, 28.4, 21.4, 38.7, 43.8,
       33.2, 27.5, 26.5, 18.6, 19.3, 20.1, 19.5, 19.5, 20.4, 19.8, 19.4,
       21.7, 22.8, 18.8, 18.7, 18.5, 18.3, 21.2, 19.2, 20.4, 19.3, 22. ,
       20.3, 20.5, 17.3, 18.8, 21.4, 15.7, 16.2, 18. , 14.3, 19.2, 19.6,
       23. , 18.4, 15.6, 18.1, 17.4, 17.1, 13.3, 17.8, 14. , 14.4, 13.4,
       15.6, 11.8, 13.8, 15.6, 14.6, 17.8, 15.4, 21.5, 19.6, 15.3, 19.4,
       17. , 15.6, 13.1, 41.3, 24.3, 23.3, 27. , 50. , 50. , 50. , 22.7,
       25. , 50. , 23.8, 23.8, 22.3, 17.4, 19.1, 23.1, 23.6, 22.6, 29.4,
       23.2, 24.6, 29.9, 37.2, 39.8, 36.2, 37.9, 32.5, 26.4, 29.6, 50. ,
       32. , 29.8, 34.9, 37. , 30.5, 36.4, 31.1, 29.1, 50. , 33.3, 30.3,
       34.6, 34.9, 32.9, 24.1, 42.3, 48.5, 50. , 22.6, 24.4, 22.5, 24.4,
       20. , 21.7, 19.3, 22.4, 28.1, 23.7, 25. , 23.3, 28.7, 21.5, 23. ,
       26.7, 21.7, 27.5, 30.1, 44.8, 50. , 37.6, 31.6, 46.7, 31.5, 24.3,
       31.7, 41.7, 48.3, 29. , 24. , 25.1, 31.5, 23.7, 23.3, 22. , 20.1,
       22.2, 23.7, 17.6, 18.5, 24.3, 20.5, 24.5, 26.2, 24.4, 24.8, 29.6,
       42.8, 21.9, 20.9, 44. , 50. , 36. , 30.1, 33.8, 43.1, 48.8, 31. ,
       36.5, 22.8, 30.7, 50. , 43.5, 20.7, 21.1, 25.2, 24.4, 35.2, 32.4,
       32. , 33.2, 33.1, 29.1, 35.1, 45.4, 35.4, 46. , 50. , 32.2, 22. ,
       20.1, 23.2, 22.3, 24.8, 28.5, 37.3, 27.9, 23.9, 21.7, 28.6, 27.1,
       20.3, 22.5, 29. , 24.8, 22. , 26.4, 33.1, 36.1, 28.4, 33.4, 28.2,
       22.8, 20.3, 16.1, 22.1, 19.4, 21.6, 23.8, 16.2, 17.8, 19.8, 23.1,
       21. , 23.8, 23.1, 20.4, 18.5, 25. , 24.6, 23. , 22.2, 19.3, 22.6,
       19.8, 17.1, 19.4, 22.2, 20.7, 21.1, 19.5, 18.5, 20.6, 19. , 18.7,
       32.7, 16.5, 23.9, 31.2, 17.5, 17.2, 23.1, 24.5, 26.6, 22.9, 24.1,
       18.6, 30.1, 18.2, 20.6, 17.8, 21.7, 22.7, 22.6, 25. , 19.9, 20.8,
       16.8, 21.9, 27.5, 21.9, 23.1, 50. , 50. , 50. , 50. , 50. , 13.8,
       13.8, 15. , 13.9, 13.3, 13.1, 10.2, 10.4, 10.9, 11.3, 12.3,  8.8,
        7.2, 10.5,  7.4, 10.2, 11.5, 15.1, 23.2,  9.7, 13.8, 12.7, 13.1,
       12.5,  8.5,  5. ,  6.3,  5.6,  7.2, 12.1,  8.3,  8.5,  5. , 11.9,
       27.9, 17.2, 27.5, 15. , 17.2, 17.9, 16.3,  7. ,  7.2,  7.5, 10.4,
        8.8,  8.4, 16.7, 14.2, 20.8, 13.4, 11.7,  8.3, 10.2, 10.9, 11. ,
        9.5, 14.5, 14.1, 16.1, 14.3, 11.7, 13.4,  9.6,  8.7,  8.4, 12.8,
       10.5, 17.1, 18.4, 15.4, 10.8, 11.8, 14.9, 12.6, 14.1, 13. , 13.4,
       15.2, 16.1, 17.8, 14.9, 14.1, 12.7, 13.5, 14.9, 20. , 16.4, 17.7,
       19.5, 20.2, 21.4, 19.9, 19. , 19.1, 19.1, 20.1, 19.9, 19.6, 23.2,
       29.8, 13.8, 13.3, 16.7, 12. , 14.6, 21.4, 23. , 23.7, 25. , 21.8,
       20.6, 21.2, 19.1, 20.6, 15.2,  7. ,  8.1, 13.6, 20.1, 21.8, 24.5,
       23.1, 19.7, 18.3, 21.2, 17.5, 16.8, 22.4, 20.6, 23.9, 22. , 11.9])

data.data #导出y的数据

array([[6.3200e-03, 1.8000e+01, 2.3100e+00, ..., 1.5300e+01, 3.9690e+02,
        4.9800e+00],
       [2.7310e-02, 0.0000e+00, 7.0700e+00, ..., 1.7800e+01, 3.9690e+02,
        9.1400e+00],
       [2.7290e-02, 0.0000e+00, 7.0700e+00, ..., 1.7800e+01, 3.9283e+02,
        4.0300e+00],
       ...,
       [6.0760e-02, 0.0000e+00, 1.1930e+01, ..., 2.1000e+01, 3.9690e+02,
        5.6400e+00],
       [1.0959e-01, 0.0000e+00, 1.1930e+01, ..., 2.1000e+01, 3.9345e+02,
        6.4800e+00],
       [4.7410e-02, 0.0000e+00, 1.1930e+01, ..., 2.1000e+01, 3.9690e+02,
        7.8800e+00]])

def linear_mode11(): #线性回归：正规方程
data =load_boston() #获取数据
x_train, x_test, y_train, y_test = train_test_split(data.data, data. target, random_state=22) #数据集划分
transfer= StandardScaler() #特征工程——标准化
x_train=transfer.fit_transform(x_train)
x_test=transfer.fit_transform(x_test)
estimator=LinearRegression() #机器学习——线性回归（正规方程）
estimator.fit(x_train,y_train)
y_predict=estimator.predict(x_test) #模型评估，获取系数等值
print("预测值为：\n",y_predict)
print("模型中的系数为：\n",estimator.coef_)
print("模型中的偏置为：\n",estimator.intercept_)
error=mean_squared_error(y_test,y_predict) #评价，均方误差
print("误差为:\n",error)
return None

linear_mode11() #调用函数

预测值为：
 [28.14790667 31.30481159 20.5173895  31.4803076  19.01576648 18.26058425
 20.57439825 18.45232382 18.46065155 32.93661269 20.3603692  27.24886071
 14.81691426 19.20872297 37.01503458 18.32036009  7.71389628 17.56196944
 30.18543811 23.60655873 18.14917545 33.84385342 28.48976083 16.9967041
 34.76065063 26.22246312 34.83857168 26.62310118 18.64402278 13.21154037
 30.37364532 14.70785748 37.18173708  8.88049446 15.06699441 16.14502168
  7.19990762 19.17049423 39.56848262 28.23663    24.62411509 16.75182833
 37.84465582  5.71770376 21.21547924 24.63882018 18.8561516  19.93416672
 15.19839712 26.29892968  7.4274177  27.14300763 29.18745146 16.27895854
  7.99799673 35.46394958 32.38905222 20.83161049 16.41464618 20.87141783
 22.92150844 23.60828508 19.32245804 38.33751529 23.87463642 18.98494066
 12.63480997  6.12915396 41.44675745 21.08894595 16.27561572 21.48546861
 40.74502107 20.4839158  36.82098808 27.0452329  19.79437176 19.64484428
 24.58763105 21.08454269 30.91968983 19.3326693  22.30088735 31.0904808
 26.36418084 20.25648139 28.81879823 20.82632806 26.01779216 19.37871837
 24.9599814  22.31091614 18.94468902 18.77414161 14.07143768 17.44450331
 24.19727889 15.86077811 20.09007025 26.51946463 20.1336741  17.02456077
 23.86647679 22.84428441 21.00754322 36.17169898 14.67959839 20.5656347
 32.46704858 33.24183156 19.81162376 26.55899048 20.90676734 16.42301853
 20.76605527 20.54658755 26.86304808 24.14176193 23.23824644 13.81640493
 15.37727091  2.79513898 28.89744167 19.80407672 21.50002831 27.5410586
 28.54270527]
模型中的系数为：
 [-0.64817766  1.14673408 -0.05949444  0.74216553 -1.95515269  2.70902585
 -0.07737374 -3.29889391  2.50267196 -1.85679269 -1.75044624  0.87341624
 -3.91336869]
模型中的偏置为：
 22.62137203166228
误差为:
 20.0621939903598

学号：202113430110

姓名：罗媛