
这个是本人在大三期间做的项目 ---- 基于MIT的Cheetah方案设计的十二自由度并联四足机器人,这个项目获得过两个国家级奖项和一个省级奖项。接下来我会将这个机器人的控制部分所有代码进行开源,并配有相关的教程博客,希望能够帮助到在学习相关领域知识或者进行项目开发的同学。
学习建议
自从MIT开源了Cheetah项目,网上出现了很多的论文解读,相关开源项目,也有很多人在原论文的基础上,对某个算法进行改进,发表了论文。对于初学者,建议从四足机器人的基础理论知识学起,再到Cheetah开源论文和其他算法改进的论文。Cheetah开源论文中有些算法细节描述不是很清楚,基本都可以通过查阅其他解读性的文章和论文,来进一步理解。
因为本人的水平有限,可能以下叙述会带有个人解读的偏见,也欢迎读者来与我联系交流:2250017028@qq.com
书籍列表
以下是我阅读过觉得比较有价值的书目,包含了四足机器人的基础理论,建议先看书籍进行知识储备,再看论文。书籍后期可以作为工具书进行查阅使用。
推荐学习路线:机械结构 -> 运动学建模及控制 -> 刚体动力学建模 -> 浮动基动力学
入门
- 《Legged-Robots-That-Balance》:讲述了弹簧倒立摆,动态控制,从单腿到双腿到四足机器人推广等算法,系统讲解了足式机器人工作的基本原理和思想,是四足机器人领域启蒙式读物。
- 《仿生四足机器人》 北理工出版:机械模型(弹簧腿)、正逆运动学、CGP控制思想等。
进阶
- 《Robot Dynamics Lecture Notes》:正逆运动学,浮动基座系统动力学与运动学,接触动力学
- 《Rigid Body Dynamics Algorithms》:空间向量代数、刚体系统动力学、刚体系统建模、正逆动力学、浮动基座动力学、接触动力学
论文列表
- 《MIT Cheetah 3: Design and Control of a Robust, Dynamic Quadruped Robot》:MIT Cheetah 3 开源论文
- 《Highly Dynamic Quadruped Locomotion via Whole-Body Impulse Control and Model Predictive Control》:MIT Cheetah mini开源论文
- 《XDog-新型电驱式四足机器人研制与测试》:宇树科技创始人的硕士学位论文,一套比较完整的四足开源方案,发表于MIT开源Cheetah项目之前,所以跟MIT所采用的结构框架不同,非常值得研读。
- 《Dynamic Locomotion in the MIT Cheetah 3 Through Convex Model-Predictive Control》:详细讲解了Cheetah项目中的MPC算法实现流程,包括动力学模型的建立和简化,MPC问题的创建以及QP求解。
- 《Passive Whole-body Control for Quadruped Robots: Experimental Validation over Challenging Terrain》:WBC算法在四足机器人上的应用,每个子任务讲的非常详细,可以用于理解WBC算法。
要点总结
下面的内容以Cheetah mini的控制架构及算法为例,进行展开叙述。
1. 控制架构
论文中给出的控制架构: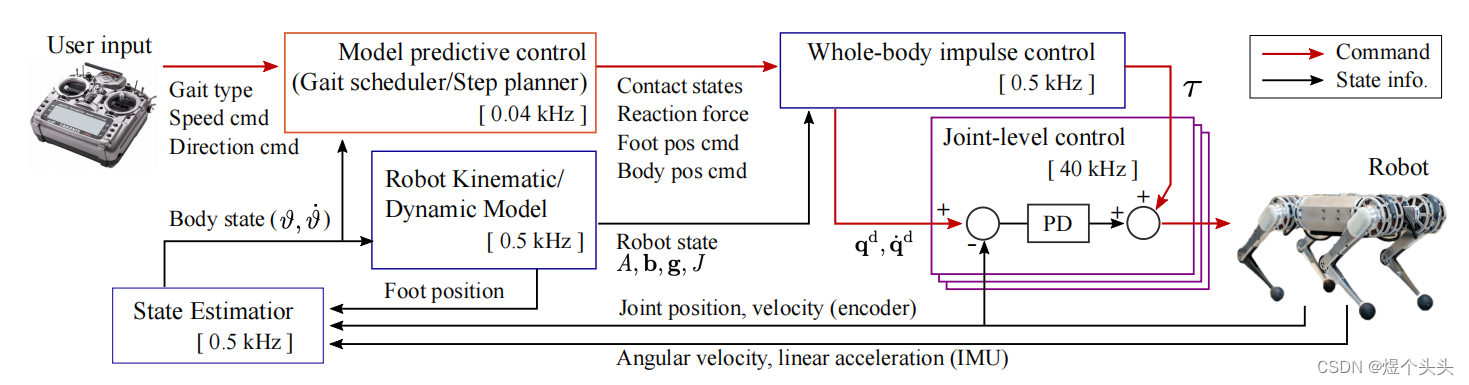
简化和总结后得到以下的控制架构: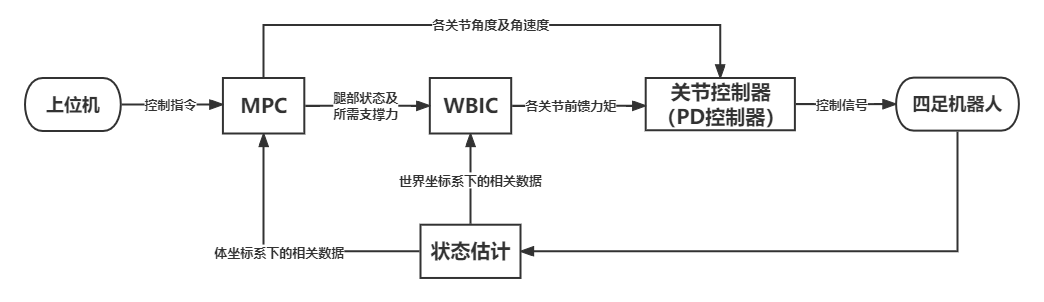
- 在整个流程中,最核心的算法是MPC和WBIC算法,但在不使用WBIC算法的时候,单MPC算法也是可以正常工作的,只要将MPC计算所得的关节目标角度,角速度,前馈力矩直接输出到关节控制器即可。
- 因为状态估计是采用了传感器数据处理得到,与实际值存在有误差,在仿真环境中验证控制算法时,可以将该环节替换为读取仿真环境中绝对正确的测量数值。
2. 步态规划(Gait Scheduler)
步态类型
四足机器人常用的步态有:stand,trot,walk等。
步态之间的属性区别在于运动周期,初始相位,转换相位。
步态名称运动周期/s起始相位转换相位Stand10(0.5, 0.5, 0.5, 0.5)1Trot0.45(0, 0.5, 0.5, 0)0.5Walk1(0.25, 0, 0.75, 0.5)0.75
运动周期:足端站立态 + 摆动态一次的时间之和。
相位:数值为0 - 1,代表一个运动周期内的各个腿部所处的状态
起始相位:每个腿部在切换到当前步态时的相位值。
转换相位:腿部从站立态切换为摆动态的相位值。
规划方式
Cheetah项目中采用的是贝赛尔曲线进行足端运动的路径规划。并且采用了动态的方法,执行流程如下:
贝塞尔曲线的详细介绍可以参考我的笔记:贝赛尔曲线学习
落足点计算
p
s
t
e
p
,
i
=
p
h
,
i
+
T
c
ϕ
2
p
˙
c
,
d
⏟
R
a
i
b
e
r
t
H
e
u
r
i
s
t
i
c
+
z
0
∣
∣
g
∣
∣
(
p
˙
c
−
p
˙
c
,
d
)
⏟
C
a
p
t
u
r
e
P
o
i
n
t
p_{step,i}=p_{h,i}+\underbrace{\frac{T_{c_\phi}}{2}{\dot{p}}_{c,d}}_{Raibert \ Heuristic}+\underbrace{\sqrt{\frac{z_0}{||g||}}({\dot{p}}_c-{\dot{p}}_{c,d})}_{Capture \ Point}
pstep,i=ph,i+Raibert Heuristic2Tcϕp˙c,d+Capture Point∣∣g∣∣z0(p˙c−p˙c,d)
T
c
ϕ
2
p
˙
c
,
d
\frac{T_{c_\phi}}{2}{\dot{p}}_{c,d}
2Tcϕp˙c,d ----根据《Legged robots that balance》中的描述,足端按照该公式确定的落足点,会使运动为对称运动,加速度为0
z
0
∣
∣
g
∣
∣
(
p
˙
c
−
p
˙
c
,
d
)
\sqrt{\frac{z_0}{||g||}}({\dot{p}}_c-{\dot{p}}_{c,d})
∣∣g∣∣z0(p˙c−p˙c,d) ----根据《Capture point: A step toward humanoid push recovery》中的描述,目标就是让落脚点趋近**capture point**,在该点腿部会获得平衡。
T
c
φ
T_{c_\varphi}
Tcφ ----理想状态下的**stance**态持续时间
z
0
z_0
z0 ----目标位置点的高度
p
h
,
i
p_{h,i}
ph,i----腿i对应髋关节电机**hip**的位置
3. 状态估计(State Estimation)
在仿真环境中,机器人的世界坐标,速度大小和方向,都可以进行读取,并基于此对机器人进行控制。
但由于四足机器人的传感器都是安装在机器人上面,一般不存在有外部传感器,所以在实际运行中,机器人的全局信息需要由IMU等传感器数据进行复杂计算得到,并且难以避免累计误差,只能尽量减少。
卡尔曼滤波(Kalman Filter)
Cheetah项目中采用了卡尔曼滤波进行状态估计。卡尔曼滤波的作用在于对不同传感器的数据进行数据融合,利用观测量并结合系统的模型来对系统的状态进行估计。
Cheetah分为以下两步进行状态估计:
航向估计(orientation):**高频的IMU的gyro数据 + 低频的IMU加速度计数据(重力偏差值)-> 旋转矩阵
0
R
b
^0R_b
0Rb**
位置/速度估计:**上述所得
0
R
b
^0R_b
0Rb + 腿部电机数据(结合机器运动学公式) -> 世界坐标系下的位置/速度**
详细公式参考论文《MIT Cheetah 3: Design and Control of a Robust, Dynamic Quadruped Robot 》中的“H. State Estimation”部分 。
卡尔曼滤波的公式推导:卡尔曼滤波
4. 关节控制器(Joint-Level Control)
Cheetah项目对关节电机的控制采用**PD控制器 + 前馈力矩
τ
\tau
τ** 的方式。
其中一共用到了两套控制器,一套用于计算前馈力矩,即补偿足端落点位置所需的力矩大小。一套用于控制各个电机逼近目标角度位置。
前馈力矩的计算
τ
f
f
,
i
=
J
i
⊤
Λ
i
(
B
a
i
,
ref
−
J
˙
i
q
˙
i
)
+
C
i
q
˙
i
+
G
i
\tau_{\mathrm{ff}, i}=\boldsymbol{J}_{i}^{\top} \boldsymbol{\Lambda}_{i}\left({ }^{\mathfrak{B}} \boldsymbol{a}_{i, \text { ref }}-\dot{\boldsymbol{J}}_{i} \dot{\boldsymbol{q}}_{i}\right)+\boldsymbol{C}_{i} \dot{\boldsymbol{q}}_{i}+\boldsymbol{G}_{i}
τff,i=Ji⊤Λi(Bai, ref −J˙iq˙i)+Ciq˙i+Gi
J
i
J_i
Ji ----足部的雅可比矩阵
Λ
i
\Lambda _i
Λi ----操作空间的惯性矩阵
B
a
i
,
r
e
f
^\mathfrak{B}a_{i,ref}
Bai,ref ----参考加速度
q
i
q_i
qi ----关节结构的向量
C
i
C_i
Ci ----科里奥利矩阵
G
i
G_i
Gi -----重力矩
τ
i
=
J
i
⊤
[
K
p
(
B
p
i
,
ref
−
B
p
i
)
+
K
d
(
B
v
i
,
r
e
f
−
B
v
i
)
]
+
τ
f
f
,
i
\boldsymbol{\tau}_{i}=\boldsymbol{J}_{i}^{\top}\left[\boldsymbol{K}_{p}\left({ }^{\mathfrak{B}} \boldsymbol{p}_{i, \text { ref }}-{ }^{\mathfrak{B}} \boldsymbol{p}_{i}\right)+\boldsymbol{K}_{d}\left({ }^{\mathfrak{B}} \boldsymbol{v}_{i, \mathrm{ref}}-{^\mathfrak{B}} \boldsymbol{v}_{i}\right)\right]+\boldsymbol{\tau}_{\mathrm{ff}, i}
τi=Ji⊤[Kp(Bpi, ref −Bpi)+Kd(Bvi,ref−Bvi)]+τff,i
电机输出力矩的计算
τ
=
K
p
(
q
d
e
s
−
q
i
)
+
K
d
(
q
d
d
e
s
−
q
d
i
)
+
τ
i
\boldsymbol{\tau}=\boldsymbol{K}_{p}\left(\boldsymbol{q}_{des}-\boldsymbol{q}_{i}\right)+\boldsymbol{K}_{d}\left(\boldsymbol{qd}_{des}-\boldsymbol{qd}_{i}\right)+\boldsymbol{\tau}_{ i}
τ=Kp(qdes−qi)+Kd(qddes−qdi)+τi
5. MPC算法(Model Predictive Control)
在Cheetah项目中,MPC算法主要用于计算保持四足机器人正常运动的情况下,每条支撑腿的足端所需的输出力。
MPC算法的公式推导参考我的学习笔记:手推MPC公式
其中,运动方程的建立将机器人看作单刚体模型:
[
I
3
…
I
3
[
p
1
p
c
]
×
…
[
p
4
p
c
]
×
]
⏟
A
F
=
[
m
(
p
¨
c
+
g
)
I
G
ω
b
˙
]
⏟
b
\underbrace{\begin{bmatrix} I_3 &\dots & I_3 \\ [p_1 p_c]\times &\dots &[p_4 p_c]\times \end{bmatrix}}_{A} F=\underbrace{\begin{bmatrix} m(\ddot{p}_c+g )\\ I_G\dot{\omega _b} \end{bmatrix}}_b
A[I3[p1pc]×……I3[p4pc]×]F=b[m(p¨c+g)IGωb˙]
上式运用了基本的牛顿运动定律
- 合力 = ma
- 合力矩 = 惯量*角加速度
6. WBIC算法(Whole-Body Impulse Control)
WBIC算法中运用到了机器人的浮动基动力学模型,吸收了MPC计算得到数据以及机器人运动学模型所得数据。
WBIC的工作原理如下:
- 将机器人的运动分为多个任务,如触地控制任务,姿态控制任务,位置/速度控制任务等,并且任务具有优先级。
- 按照优先级的顺序,依次求解各个任务所需的电机前馈力矩输出公共解。
- 输出电机控制力矩
WBC的公式推导及应用可以参考我的学习笔记:
手推WBC公式
WBC控制的实际应用
版权归原作者 煜个头头 所有, 如有侵权,请联系我们删除。