知识图谱嵌入模型 (KGE) 的总结和比较

知识图谱嵌入(KGE)是一种利用监督学习来学习嵌入以及节点和边的向量表示的模型。它们将“知识”投射到一个连续的低维空间，这些低维空间向量一般只有几百个维度（用来表示知识存储的内存效率）。向量空间中，每个点代表一个概念，每个点在空间中的位置具有语义意义，类似于词嵌入。

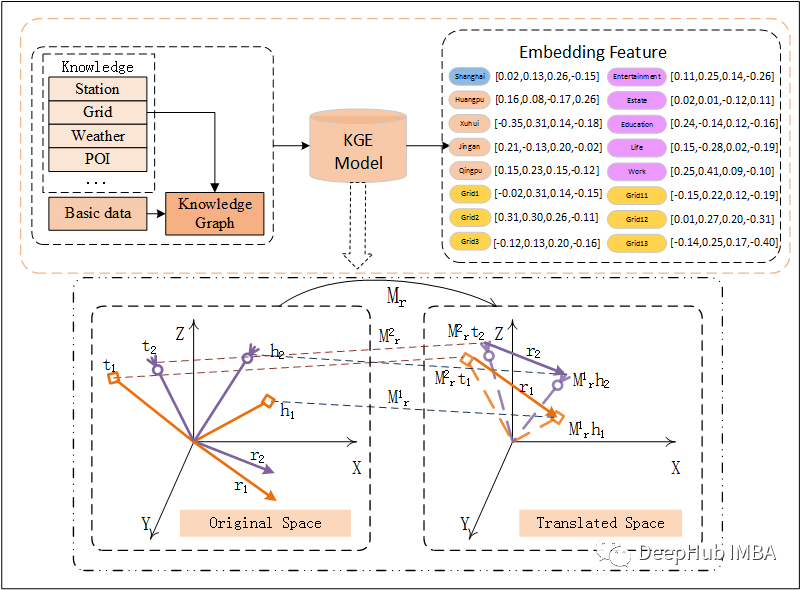
一个好的KGE 应该具有足够的表现力来捕获 KG 属性，这些属性解决了表示关系的独特逻辑模式的能力。并且KG 可以根据要求添加或删除一些特定属性。KGE算法可分为两类：

• 翻译距离模型（translation distance models），如TransE、TransH、TransR、TransD等。
• 语义匹配模型（semantic matching models），如DistMult。

以下是常见的KGE 模型在捕获关系类型方面的比较，我们将对这些常见的模型进行比较

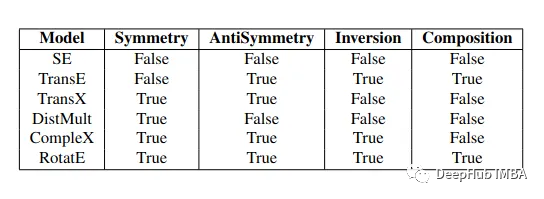
翻译距离模型

TransE

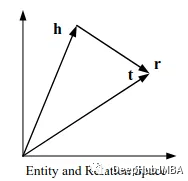
提出了一种基于翻译的知识图谱嵌入模型，可以捕获多关系图中的翻译方差不变性现象。知识图谱中的事实是用三元组 ( h , l , t ) 表示的，transE算法的思想非常简单，它受word2vec平移不变性的启发，希望h + l ≈ t h+l≈th+l≈t。

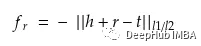
这里的l1/l2是范数约束。

TransE的伪代码如下：

TransE多次在大规模知识图谱方面表现出良好的性能。但是它不能有效地捕获复杂的关系，如一对多和多对多。

TransH

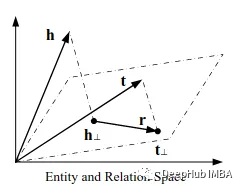
TransH根据关系为每个实体提供不同的表示向量。TransH的工作原理是为每个关系发布一个完全独立的特定于关系的超平面，这样与它关联的实体仅在该关系的上下文中具有不同的语义。TransH将实体嵌入向量h和t投影到映射向量Wᵣ方向的超平面(关系特定)。

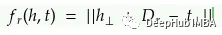
其中Dᵣ表示关系特定的平移向量，h和t的计算方法如下:

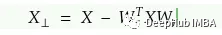
TransH 在一定程度上解决了复杂关系问题。它采用相同的向量特征空间。

TransR

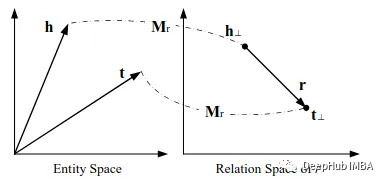
TransR的理念与TransH非常相似。但它引入了特定于关系的空间，而不是超平面。实体表示为实体空间Rᵈ中的向量，每个关系都与特定空间Rᵏ相关联，并建模为该空间中的平移向量。给定一个事实，TransR首先将实体表示h和t投影到关系r特定的空间中:

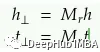
这里Mᵣ是一个从实体空间到r的关系空间的投影矩阵，评分函数定义为

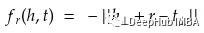
它能够对复杂的关系建模。但是每个关系需要O(dk)个参数。没有TransE/TransH的简单性和效率。

TransD

TransD是TransR的改进。它采用映射矩阵，为头部和尾部实体生成两个独立的映射矩阵。它使用两个嵌入向量来表示每个实体和关系。第一个嵌入向量表示实体和关系的语义，第二个嵌入向量生成两个动态投影矩阵，如下图所示。

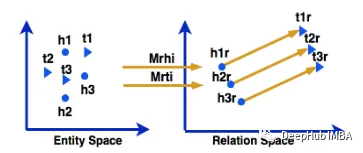
评分函数如下：

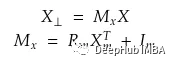
下表是总结所有翻译距离模型的对比

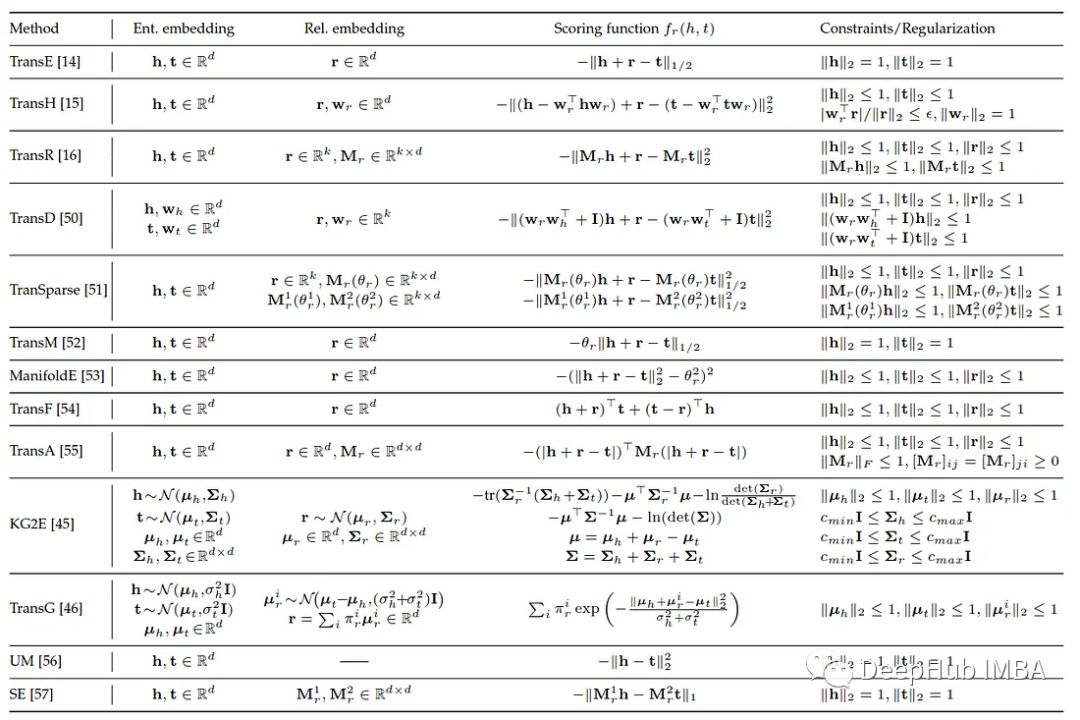
语义匹配模型

RESCAL

RESCAL将每个实体与一个向量相关联，捕获其潜在语义。每个关系都表示为一个矩阵，它模拟了潜在因素之间的成对相互作用。事实(h,r,t)的分数由双线性函数定义。

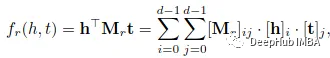
其中h,t∈Rᵈ是实体的向量表示，Mᵣ∈Rᵈ*ᵈ是与该关系相关的矩阵。这个分数捕获了h和t的所有分量之间的成对相互作用，每个关系需要O(d²)个参数，并进一步假设所有 Mᵣ 在一组通用的 rank-1 指标上分解。

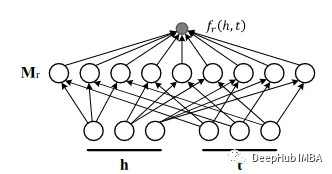
它最大的问题是计算复杂且成本高。

TATEC

TATEC模型不仅有三种相互关系，它还包含双向交互，例如实体和关系之间的交互。评分函数为

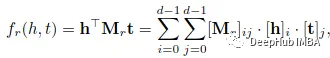
其中D是所有不同关系共享的对角矩阵。

DistMult

通过将Mᵣ限制为对角矩阵，DistMult简化了RESCAL。对于每个关系r，引入一个向量r∈rᵈ，并要求Mᵣ= diag(r),评分函数如下：

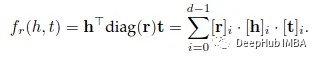
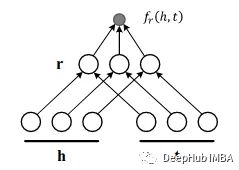
DistMult优点就是计算简单，成本低。但是因为模型过于简化，只能处理对称关系。对于一般kg来说，它不够强大。

Holographic Embeddings(HolE)

HolE结合了RESCAL的表达能力和DistMult的效率和简单性。它将实体和关系重新表示为Rᵈ中的向量。给定一个事实(h,r,t)，通过使用循环相关操作，首先将实体表示组合成h*t∈rᵈ：

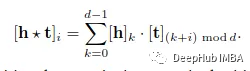
采用*的主要目的是利用压缩张量积形式的复合表示的降低复杂性。HolE利用了快速傅里叶变换，可以通过以下方式进一步加速计算过程:

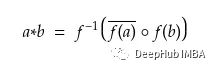
HolE每个关系只需要O(d)个参数，这比RESCAL更有效。但是HolE不能对不对的称关系建模，但在一些研究论文中，把它与扩展形式HolEX混淆了，HolEX能够处理不对称关系。

Complex Embeddings (ComplEx)

Complex通过引入复值嵌入来扩展DistMult，以便更好地建模非对称关系。在ComplEx中，实体和关系嵌入h,r,t不再位于实空间中，而是位于复空间中，例如Cᵈ。

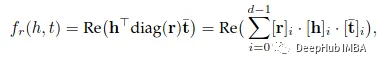
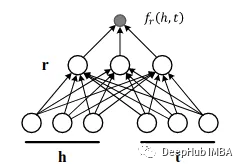
这个评分函数不再对称，来自非对称关系的事实可以根据所涉及实体的顺序获得不同的分数。作为共轭对称施加于嵌入的特殊情况，HolE可以被包含在ComplEx中。

ANALOGY

ANALOGY 扩展了RESCAL，可以进一步对实体和关系的类推属性建模。它采用了双线性评分函数。

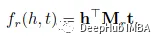
DistMult, HolE和ComplEx都可以作为特殊情况在ANALOGY上实现。

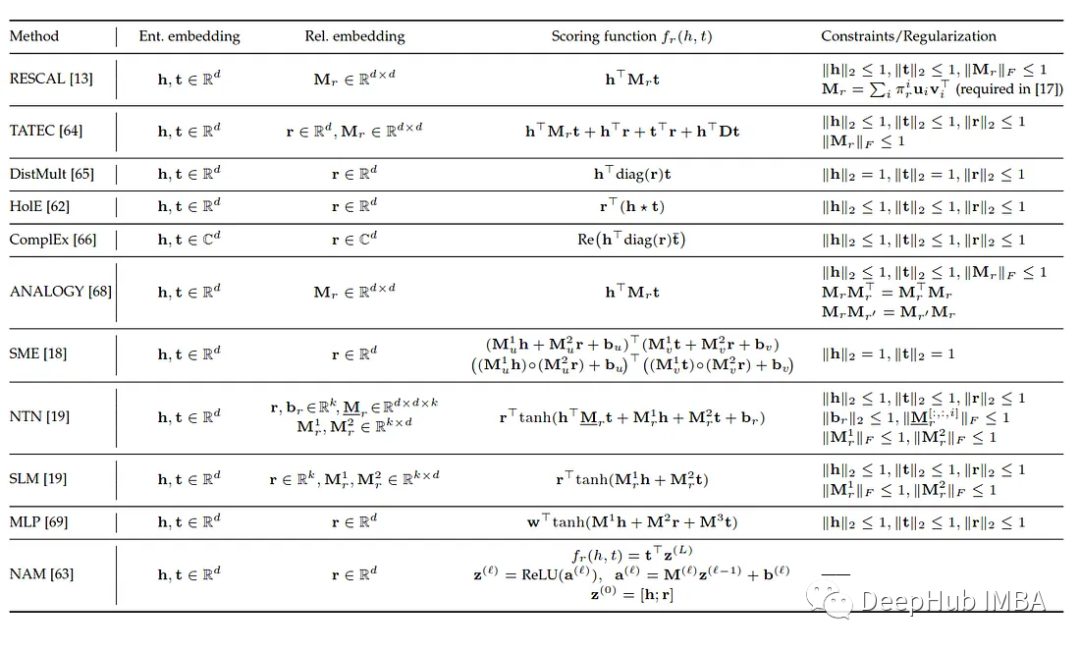
以下是语义匹配模型的对比总结：

Deep Scoring Functions

对于深度学习进步，还出现了基于深度学习的评分函数

ConvE

ConvE是第一个使用卷积神经网络(CNN)来预测知识图谱中缺失环节的模型之一。与完全连接的密集层不同，cnn可以通过使用很少的参数学习来帮助捕获复杂的非线性关系。ConvE在多个维度上实现了不同实体之间的本地连接。

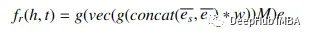
concat为连接运算符，*表示卷积，eₛ和eᵣ分别负责主题单元和关系单元的二维重塑。

ConvE不能捕获三元嵌入的全局关系

ConvKB

ConbKB使用1D卷积来保留TransE的解释属性，捕获实体之间的全局关系和时间属性。该方法将每个三元网络嵌入为三段网络，并将其馈送到卷积层，实现事实的维类之间的全局连接。

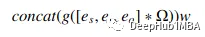
其中Ω(过滤器集)，e(权重向量)表示共享参数。

HypER

HypER将每个关系的向量嵌入通过密集层投影后完全重塑，然后调整每层中的一堆卷积通道权重向量关系，这样可以有更高的表达范围和更少的参数。

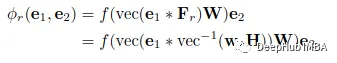
vec是将一个向量重新塑造为一个矩阵，非线性f是ReLU。

模型的空间复杂度和时间复杂度的比较

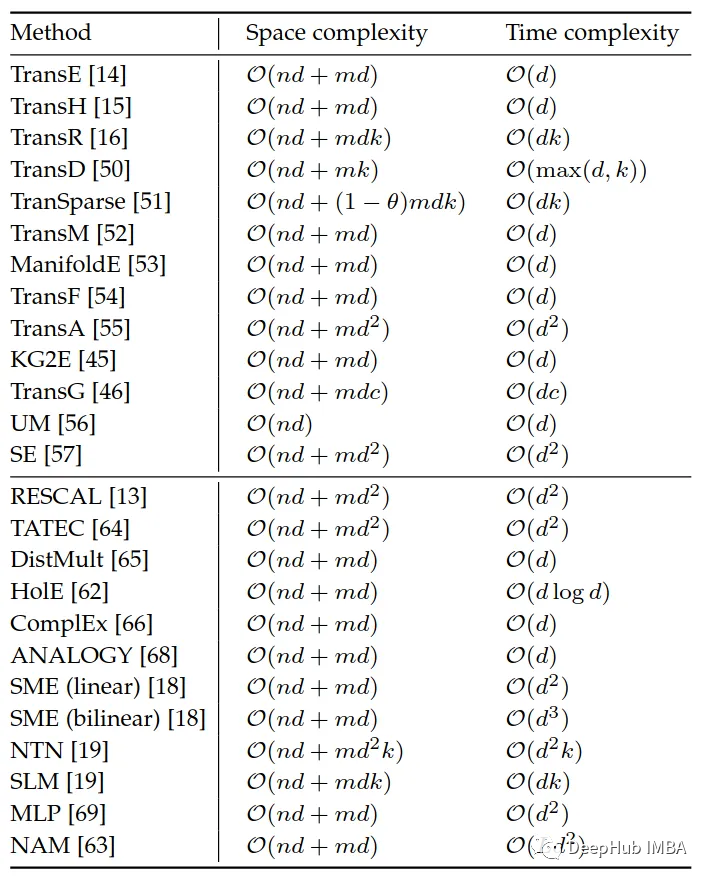
引用：

1. Knowledge Graph Embedding: A Survey of Approaches and Applications by Quan Wang, Zhendong Mao, Bin Wang, and Li Guo
2. A. Bordes, N. Usunier, A. Garcia-Duran, J. Weston, O. Yakhnenko, Translating embeddings for modeling multi-relational data, Advances in neural information processing systems 26 (2013)
3. Z. Wang, J. Zhang, J. Feng, Z. Chen, Knowledge graph embedding by translating on hyperplanes, in: Proceedings of the AAAI Conference on Artificial Intelligence, volume 28.
4. Y. Lin, Z. Liu, M. Sun, Y. Liu, X. Zhu, Learning entity and relation embeddings for knowledge graph completion, in: Twenty-ninth AAAI conference on artificial intelligence.
5. G. Ji, S. He, L. Xu, K. Liu, J. Zhao, Knowledge graph embedding via dynamic mapping matrix, in: Proceedings of the 53rd Annual Meeting of the Association for Computational Linguistics and the 7th International Joint Conference on Natural Language Processing (Volume 1: Long Papers), pp. 687–696.
6. M. Nickel, V. Tresp, H.-P. Kriegel, A three-way model for collective learning on multi-relational data, in: Icml.
7. B. Yang, W.-t. Yih, X. He, J. Gao, L. Deng, Embedding entities and relations for learning and inference in knowledge bases, arXiv preprint arXiv:1412.6575 (2014).
8. M. Nickel, L. Rosasco, T. Poggio, Holographic embeddings of knowledge graphs, in: Proceedings of the AAAI Conference on Artificial Intelligence, volume 30.
9. Y. Xue, Y. Yuan, Z. Xu, A. Sabharwal, Expanding holographic embeddings for knowledge completion., in:NeurIPS, pp. 4496–4506.
10. K. Hayashi, M. Shimbo, On the equivalence of holographic and complex embeddings for link prediction, in:Proceedings of the 55th Annual Meeting of the Association for Computational Linguistics (Volume 2: Short Papers), pp. 554–559.
11. H. Liu, Y. Wu, Y. Yang, Analogical inference for multi-relational embeddings, in: International conference on machine learning, PMLR, pp. 2168–2178.
12. T. Dettmers, P. Minervini, P. Stenetorp, S. Riedel, Convolutional 2d knowledge graph embeddings, in: Thirty second AAAI conference on artificial intelligence.
13. D. Q. Nguyen, T. D. Nguyen, D. Q. Nguyen, D. Phung, A novel embedding model for knowledge base completion based on convolutional neural network, arXiv preprint arXiv:1712.02121 (2017).
14. I. Balaževi ́c, C. Allen, T. M. Hospedales, Hypernetwork knowledge graph embeddings, in: International Conference on Artificial Neural Networks, Springer, pp. 553–565
15. S. Sabour, N. Frosst, G. E. Hinton, Dynamic routing between capsules, arXiv preprint arXiv:1710.09829 (2017).

作者：Shreyash Pandey