【数据结构】数组区间更新-IndexTree（树状数组）

在前段时间，我们介绍过线段树，线段树是解决在数组区间上进行快速的增删改查操作。而今天我们讲得IndexTree也是为了达到这样类似的效果。
本期文章源码：GitHub

目录

一、介绍

例题：给定一个数组arr，arr的长度是1000，现在问你如何快速的计算500 ~ 1000之间，所有的数的累加和？？

可能你会说直接一个for循环，从500开始累加不就行了吗？ 这样确实可以达到目的，但是还是不够快。

又或许，你会想到用前缀和数组，先计算每一个index，从0下标一直累加到index位置。这样一个前缀和数组，也是能达到相应的效果。如下：

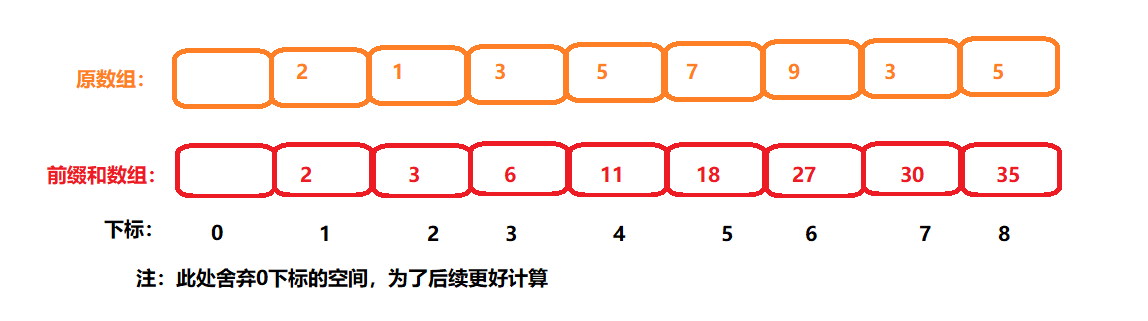
如上图所示，假设我们需要计算 3 ~7 范围上的累加和，我们只需要用 （1 ~ 7）累加和减去（1 ~ 2）累加和，这样就能得到想要的答案。

但还是存在一个问题，计算前缀和当然很简单，假设原数组的数据经常改动，那么前缀和数组也需要跟着改动，由于这个问题，导致使用前缀和数组计算范围上的累加和存在一定的缺陷。所以最后就进行优化，搞出了现在听说的树状数组IndexTree。

IndexTree原理：

在上述的前缀和数组的基础之上，我们需要改一下前缀和的计算规则，如下所示：

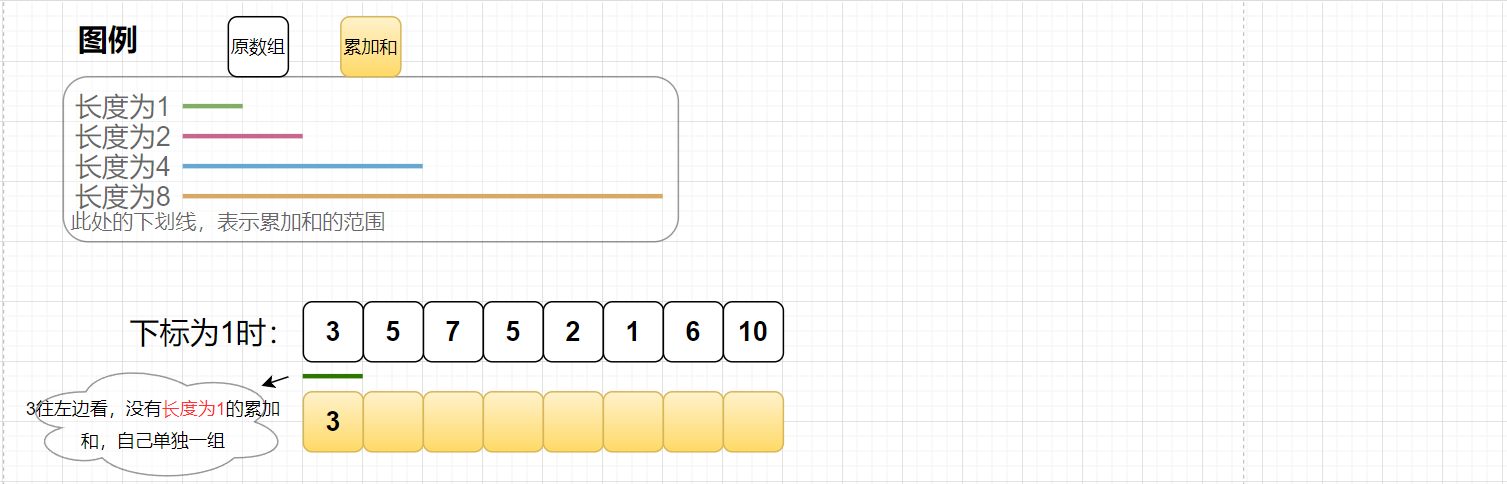
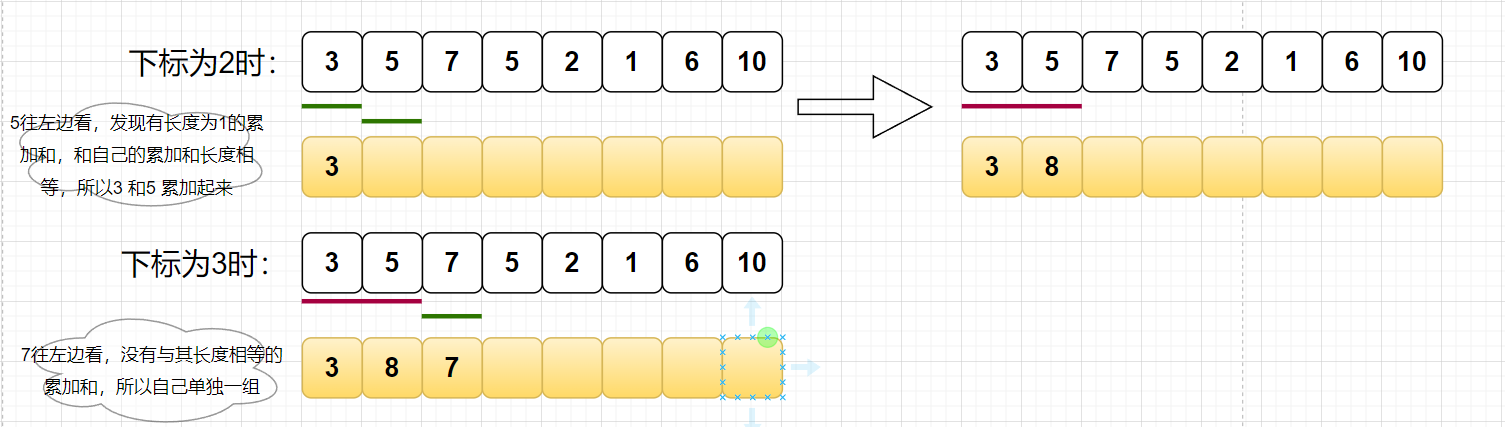
总结起来就是，在计算index位置的累加和时，先看左边是否有长度一样的累加和，有的话，二者就合并在一起，形成2倍长度。

然后你就会发现，在下标是（2的某次幂时），此时的位置是计算1index位置所有的累加和，例如4下标，就是管理14范围全部的累加和。

这样的设计，有何作用呢？

例如，12下标的二进制是 0000 1100，将最靠后的1，放到最后一个位置去，如下：

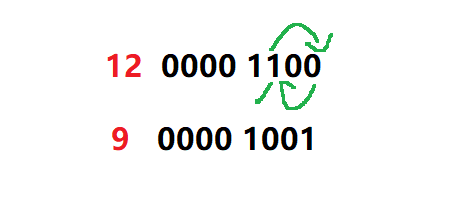
移动之后的值就是9，此时你会发现 下标12所管理的累计和就是 9 ~ 12范围。如图

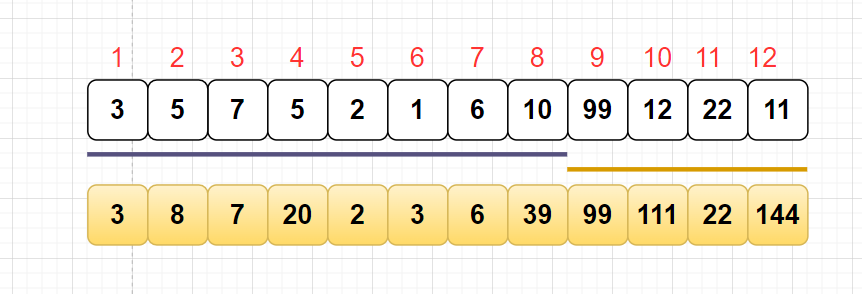
就是根据这样的规律，我们可以在改动原数组的数据时，能够很快的查询到，这次改动会影响到哪些位置的数据，这样就能很快的进行修改。

比如，我们现在更改9 ~ 12范围内的任意一个数，就假设改动下标10的数据吧，可以根据以下计算规则，就能计算到会影响12下标。

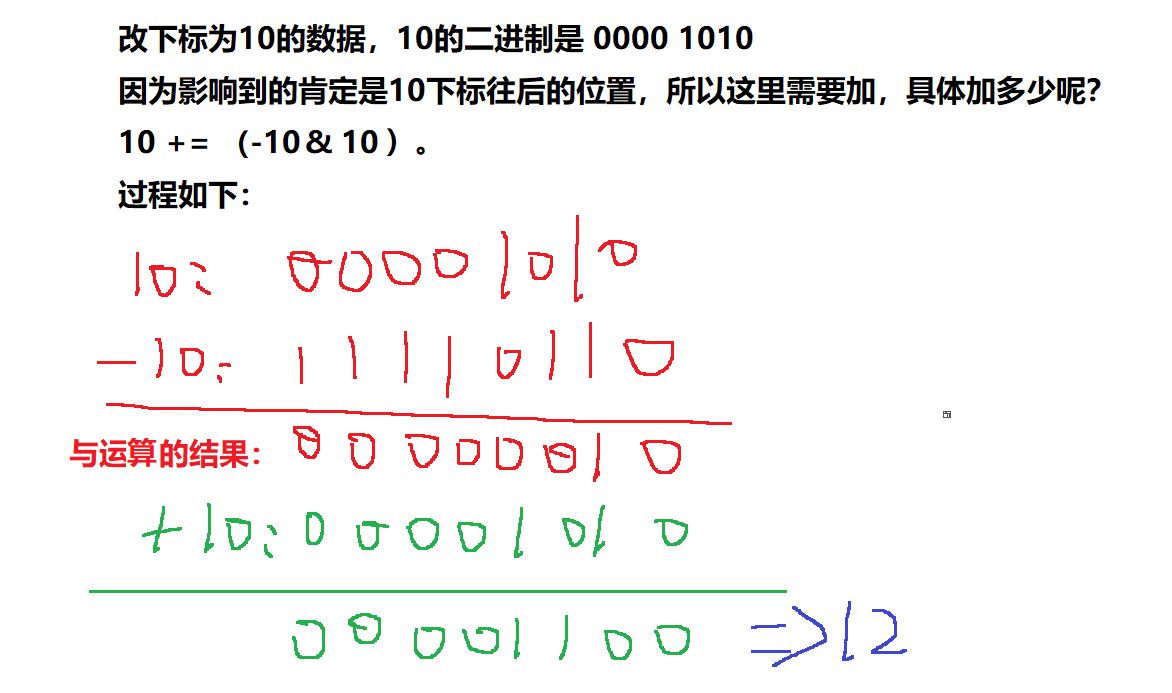
线段树和IndexTree的区别？？？

可能你会说，你上面说的是区间更新操作，线段树也可以完成啊，为啥非要再搞一个IndexTree？闲的没事做吗？

显然不是的。确实区间更新操作，线段树能够做到，但是只对一个下标进行更新，使用线段树，就有点多余了。比如add(10, 10, -100)，在L= 10，R=10的位置，插入-100，线段树这样做并不够高效，而IndexTree就是为了实现这样的，只改定一个位置的数据。

并且indexTree，能够很好的改成二维的效果，比如给你一个二维数组，计算某一块矩形的面积，这种就可以将IndexTree改为二维数组的形式，也是能够很快的解决问题。

简单来说，线段树确实能够实现区间更新，但是不好改成二维数组的形式；IndexTree，能够实现单点更新，还能改二维数组，也是一种比较好用的数据结构。

LeetCode矩形面积：https://leetcode-cn.com/problems/range-sum-query-2d-mutable/

二、IndexTree的实现

1、add方法

在知道原理以后，我们就可以很轻松的写出相应的代码了，关键就是记住

index += （-index & index）

publicclassIndexTree{privateint[] nums;//原数组privateint[] tree;//累加和数组privateint length;//数组长度publicIndexTree(intN){this.length =N+1;//要舍弃0下标的空间this.nums =newint[length];this.tree =newint[length];}//在index位置放入，val值  publicvoidadd(int index,int val){if(index <1|| index >= length){return;//越界的情况}
        nums[index]+= val;//改动原数组for(int i = index; i < length; i +=(i &-i)){
            tree[i]+= val;//改累加和数组}}}

2、update方法

更新操作，是将原数组的数据，改为另外一个数据。影响的范围还是从index位置向后的情况。与add方法类似

publicvoidupdate(int index,int newVal){if(index <1|| index >= length){return;//越界的情况}int value = newVal - nums[index];//计算与之前的差值，最后累加到tree数组即可
    nums[index]= newVal;//改为新的数据for(int i = index; i < length; i +=(i &-i)){
        tree[i]+= value;//累加差值即可}}

3、query方法

add方法和update方法，改动数据，是影响到index后面位置的数据。而query查询方法，是从1~index位置进行累加，所有从index位置开始计算，每次需要减去（index & -index）。

//查询1 ~ index位置的累加和publicintquery(int index){if(index <1|| index >= length){return-1;//越界的情况}int res =0;for(int i = index; i >0; i -=(i &-i)){
        res += tree[i];}return res;}

好啦，本期更新到此结束，我们下期见！！！