R语言-多元统计学分析课程报告

本文我们应用的软件为R语言，进行多元统计分析，所用的数据集为鸢尾花数据集；我们进行了Bayes判别、Fisher判别、系统聚类法、k-均值聚类和主成分分析。

# 导入鸢尾花数据集
data<-read.csv("E:/数学专业/多元统计学上机作业/iris.csv",header=T)
iris<-data[,-6]
# 分析变量之间的关系
data1<-as.matrix(data[,-c(5,6)]) # 去除最后一行符号行

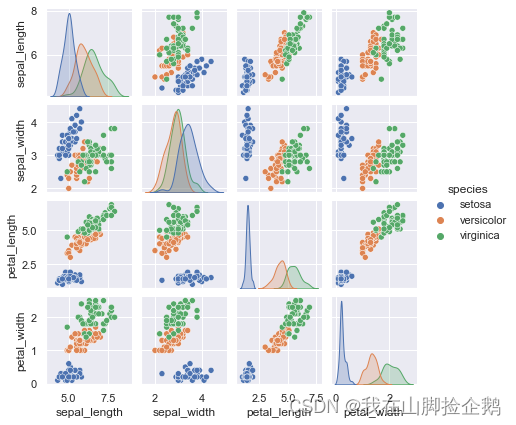
我们首先画出变量之间的散点图：

# 画出变量之间的散点图
pairs(data1)

紧接着我们运用Fisher判别：

# Fisher判别
head(data)
by(data[,1:4],data[,5],colMeans) # 比较三类鸢尾花在4个变量上的均值
library(MASS)
z<-lda(species~.,data[,-6],prior=c(1,1,1)/3) # Fisher判定，设定三个类别的先验概率均为1/3
z
iris.lda.values<-predict(z) # 对现有样本进行预测
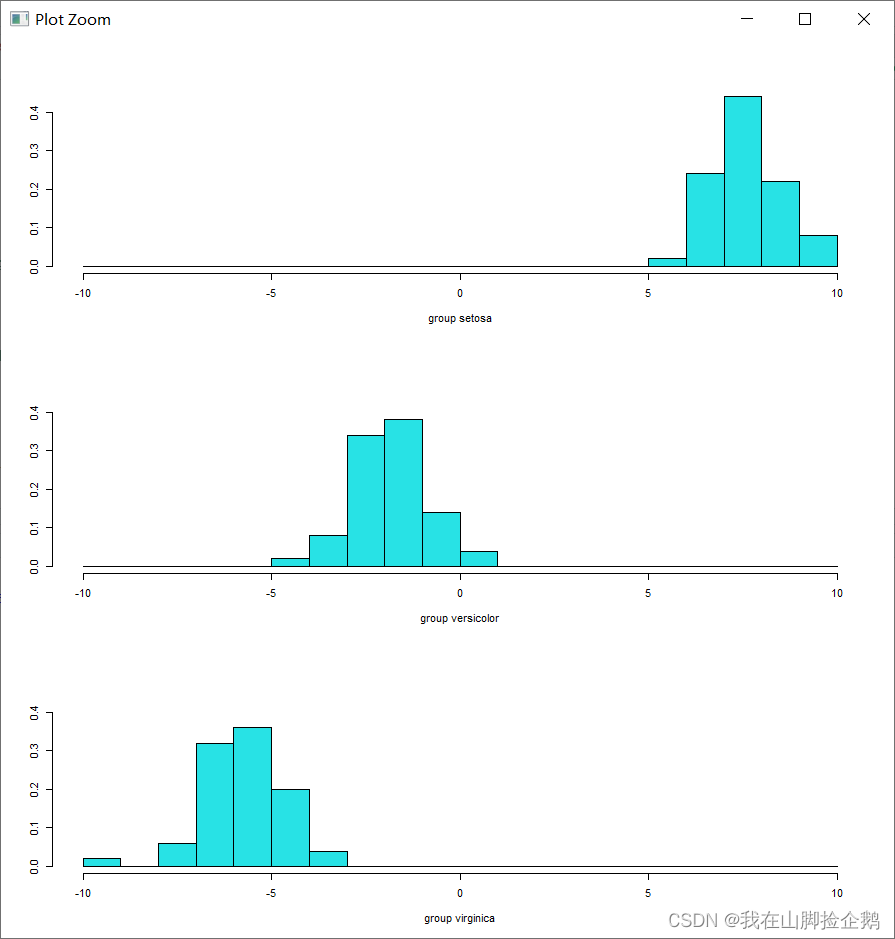
ldahist(data=iris.lda.values$x[,1],g=iris$species) # 输出在第一方向上，三个类别投影的直方图
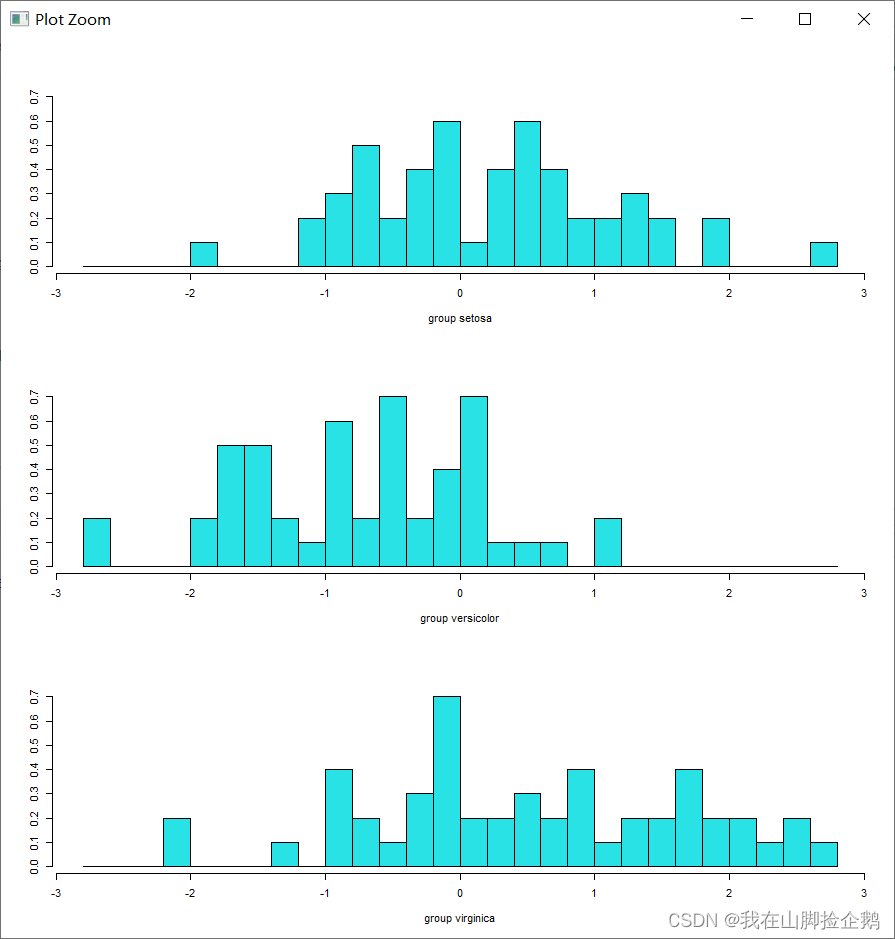
ldahist(data=iris.lda.values$x[,2],g=iris$species)

可以得到结果为 ：

紧接着应用Bayes判别，将数据分为训练集与测试集可以得到准确率吧达到97%。

在应用k-均值聚类，得到

# k-means聚类
install.packages("factoextra")
library(ggplot2)
library(factoextra)
library(cluster)
kmeans(data1[,1:4],3,nstart = 100) # 使用足够大的nstart，更容易得到对于最小的RSS值得模型

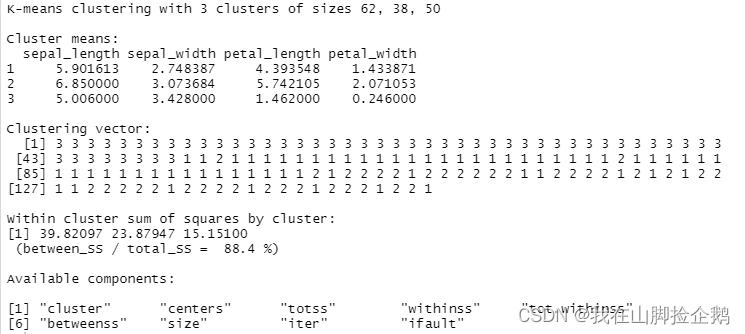
画出碎石图，可以知道我们将样本分为三类是最好的结果，这一结果也符合我们数据的本来特性。

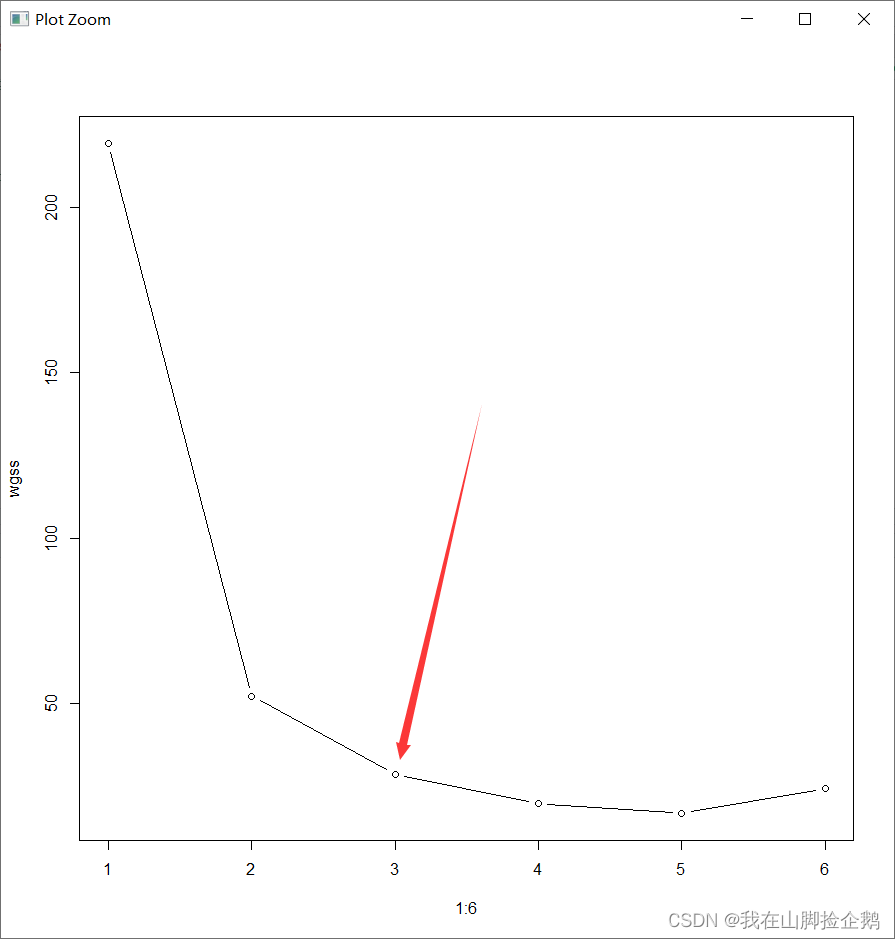
最后用主成分分析可以得到

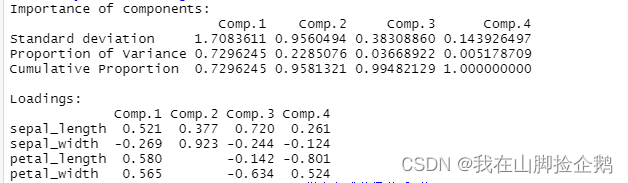
# 主成分分析
PCA1<-princomp(data1,cor=T)
summary(PCA1,loadings=T)
samplePC<-round(PCA1$scores,3) # 取样本主成分得分后3位
round(predict(PCA1),3)
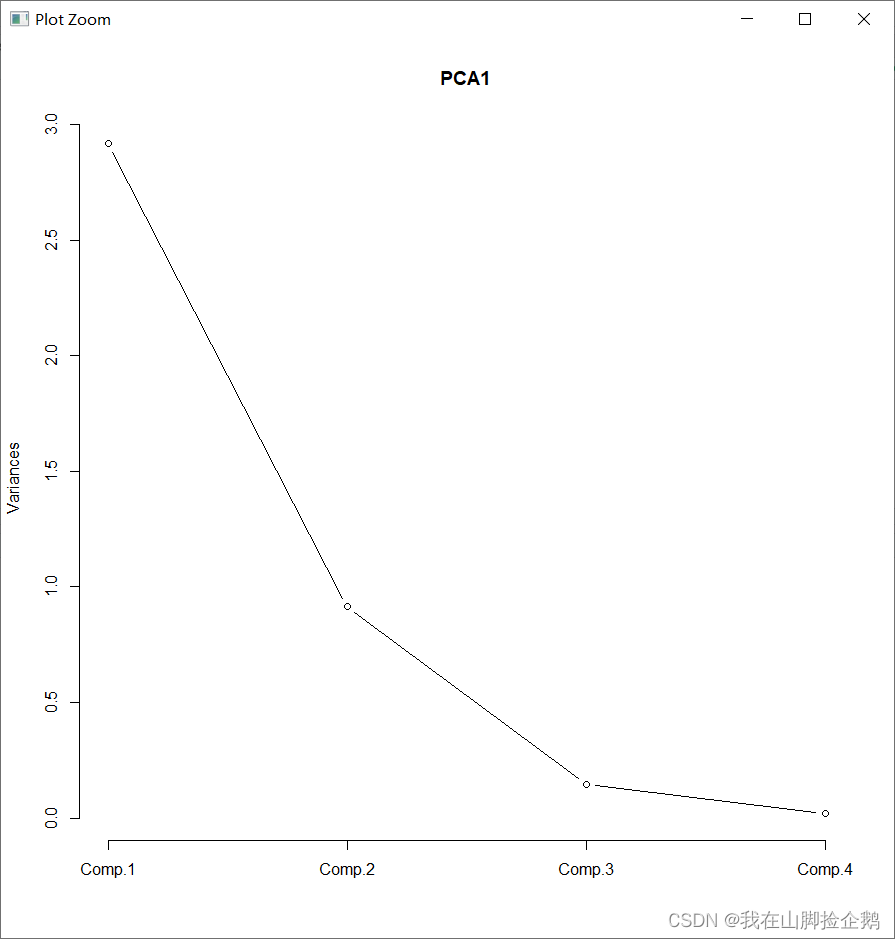
screeplot(PCA1,type='lines') # 画碎石图
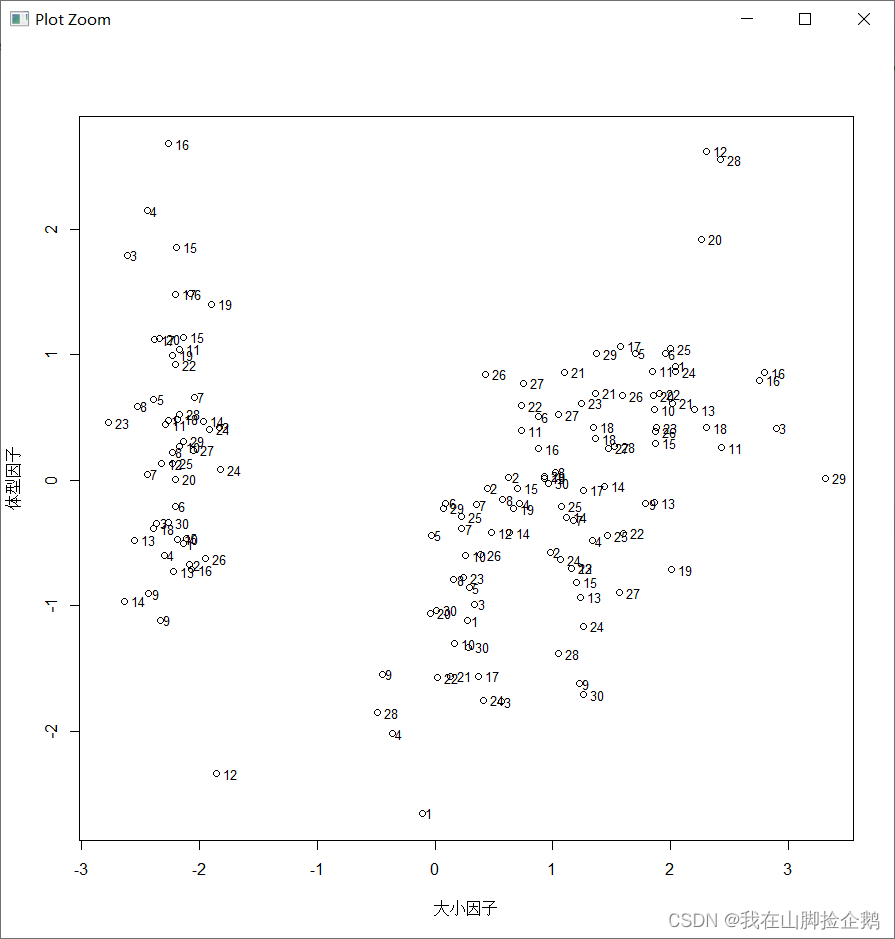
plot(samplePC[,1],samplePC[,2],xlab='大小因子',ylab='体型因子')
text(samplePC[,1],samplePC[,2],1:30,adj=-0.5,cex=0.8)