50年前Kernighan、Ritchie和他们的C语言书的第一版开始,人们就知道单精度“float”类型有32位大小,双精度类型有64位大小。还有一种具有扩展精度的80位“长双精度”类型,这些类型几乎涵盖了浮点数据处理的所有需求。但是在最近几年,尤其是今年LLM的兴起,为了减小模型的存储和内存占用,开发人员开始尽可能地缩小浮点类型。
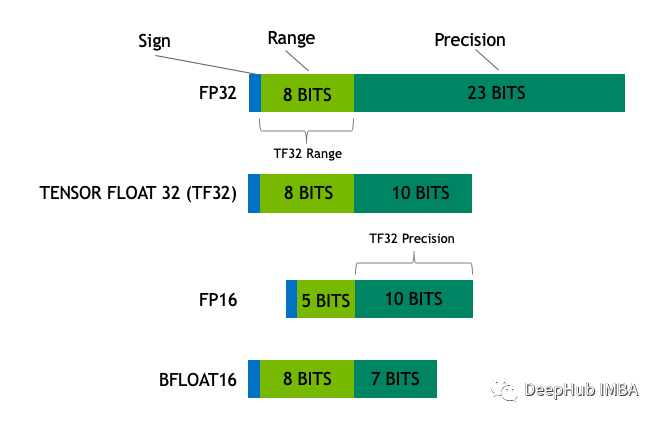
在本文中,我们将介绍最流行的浮点格式,创建一个简单的神经网络,并了解它是如何工作的。
“标准”32位浮点数
我们先回顾一下标准格式。IEEE 754浮点运算标准由IEEE于1985年制定。32浮点型的典型数字是这样的:

第一个比特(bit)是一个符号,接下来的8个比特代表一个指数,最后一个比特代表尾数。最终值的计算公式为:
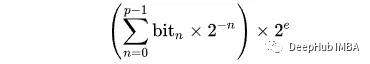
我们创建一个辅助函数以二进制形式打印浮点值:
import struct
def print_float32(val: float):
""" Print Float32 in a binary form """
m = struct.unpack('I', struct.pack('f', val))[0]
return format(m, 'b').zfill(32)
print_float32(0.15625)
# > 00111110001000000000000000000000
再创建一个逆向转换函数,这将在后面有用:
def ieee_754_conversion(sign, exponent_raw, mantissa, exp_len=8, mant_len=23):
""" Convert binary data into the floating point value """
sign_mult = -1 if sign == 1 else 1
exponent = exponent_raw - (2 ** (exp_len - 1) - 1)
mant_mult = 1
for b in range(mant_len - 1, -1, -1):
if mantissa & (2 ** b):
mant_mult += 1 / (2 ** (mant_len - b))
return sign_mult * (2 ** exponent) * mant_mult
ieee_754_conversion(0b0, 0b01111100, 0b01000000000000000000000)
#> 0.15625
作为开发,你肯定知道浮点类型的准确性是有限的,比如这个:
val = 3.14
print(f"{val:.20f}")
# > 3.14000000000000012434
在一般情况下,这不是一个大问题,但是我们拥有的比特位越少,得到的精度就越低。
16位浮点数
早期对这种格式的需求并不大,直到2008年才将16位浮点类型添加到IEEE 754标准中。它有一个符号位,5个指数位和10位尾数(分数):

他的转换逻辑与32位浮点数相同,但精度较低。以二进制形式打印一个16位浮点数:
import numpy as np
def print_float16(val: float):
""" Print Float16 in a binary form """
m = struct.unpack('H', struct.pack('e', np.float16(val)))[0]
return format(m, 'b').zfill(16)
print_float16(3.14)
# > 0100001001001000
使用之前使用的方法,我们可以进行反向转换:
ieee_754_conversion(0, 0b10000, 0b1001001000, exp_len=5, mant_len=10)
# > 3.140625
我们还可以找到Float16中可以表示的最大值:
ieee_754_conversion(0, 0b11110, 0b1111111111, exp_len=5, mant_len=10)
#> 65504.0
这里使用0b11110,是因为在IEEE 754标准中,0b11111是为“无穷大”保留的。同理还可以找到可能的最小值:
ieee_754_conversion(0, 0b00001, 0b0000000000, exp_len=5, mant_len=10)
#> 0.00006104
对于大多数开发人员来说,像这样的类型是一种“未知的领域”,因为c++中也没有标准的16位浮点类型。
16位" bfloat " (BFP16)
这种浮点格式是由谷歌团队开发的,它是专门为机器学习设计的(名字中的“B”也代表“大脑”)。该类型是对“标准”16位浮点数的修改:指数被扩大到8位,因此“bfloat16”的动态范围实际上与float-32相同。但尾数的大小被减少到7位:

让我们做一个和之前类似的计算:
ieee_754_conversion(0, 0b10000000, 0b1001001, exp_len=8, mant_len=7)
#> 3.140625
可以看到由于指数较大,bfloat16格式具有更宽的范围:
ieee_754_conversion(0, 0b11111110, 0b1111111, exp_len=8, mant_len=7)
#> 3.3895313892515355e+38
这比前面示例中的65504.0要好得多,但是正如前面提到的:因为尾数中的位数更少,所以bfloat16的精度更低,可以在Tensorflow中测试这两种类型:
import tensorflow as tf
print(f"{tf.constant(1.2, dtype=tf.float16).numpy().item():.12f}")
# > 1.200195312500
print(f"{tf.constant(1.2, dtype=tf.bfloat16).numpy().item():.12f}")
# > 1.203125000000
8位浮点(FP8)
这种(相对较新的)格式是在2022年提出的,它也是为机器学习而创建的——因为模型变得更大,将它们放入GPU内存是一个挑战。FP8格式有两种变体:E4M3(4位指数和3位尾数)和E5M2(5位指数和2位尾数)。

让我们来获取两种格式的最大可能值:
ieee_754_conversion(0, 0b1111, 0b110, exp_len=4, mant_len=3)
# > 448.0
ieee_754_conversion(0, 0b11110, 0b11, exp_len=5, mant_len=2)
# > 57344.0
也可以在Tensorflow中使用FP8:
import tensorflow as tf
from tensorflow.python.framework import dtypes
a_fp8 = tf.constant(3.14, dtype=dtypes.float8_e4m3fn)
print(a_fp8)
# > 3.25
a_fp8 = tf.constant(3.14, dtype=dtypes.float8_e5m2)
print(a_fp8)
# > 3.0
让我们在这两种类型中画一个正弦波:
import numpy as np
import tensorflow as tf
from tensorflow.python.framework import dtypes
import matplotlib.pyplot as plt
length = np.pi * 4
resolution = 200
xvals = np.arange(0, length, length / resolution)
wave = np.sin(xvals)
wave_fp8_1 = tf.cast(wave, dtypes.float8_e4m3fn)
wave_fp8_2 = tf.cast(wave, dtypes.float8_e5m2)
plt.rcParams["figure.figsize"] = (14, 5)
plt.plot(xvals, wave_fp8_1.numpy())
plt.plot(xvals, wave_fp8_2.numpy())
plt.show()
可以看到,有一些差别,但是都还不错。

可以明显看到一些精度的损失,但这个图像看起来仍然像正弦波!
4位浮点类型
现在让我们来看看最“疯狂”的东西——4位浮点值!4位浮点数(FP4)是遵循IEEE标准的最小可能值,具有1位符号,2位指数和1位尾数:

第二种可能的4位实现是所谓的NormalFloat (NF4)数据类型。NF4值针对保存正态分布变量进行了优化。其他数据类型很难做到这一点,但所有可能的NF4值都可以很容易地打印在一个列表中:
[-1.0, -0.6961928009986877, -0.5250730514526367, -0.39491748809814453,
-0.28444138169288635, -0.18477343022823334, -0.09105003625154495, 0.0,
0.07958029955625534, 0.16093020141124725, 0.24611230194568634, 0.33791524171829224,
0.44070982933044434, 0.5626170039176941, 0.7229568362236023, 1.0]
FP4和NF4类型都在bitsandbytes库中有相应的实现。作为一个例子,让我们将[1.0,2.0,3.0,4.0]数组转换为FP4:
from bitsandbytes import functional as bf
def print_uint(val: int, n_digits=8) -> str:
""" Convert 42 => '00101010' """
return format(val, 'b').zfill(n_digits)
device = torch.device("cuda")
x = torch.tensor([1.0, 2.0, 3.0, 4.0], device=device)
x_4bit, qstate = bf.quantize_fp4(x, blocksize=64)
print(x_4bit)
# > tensor([[117], [35]], dtype=torch.uint8)
print_uint(x_4bit[0].item())
# > 01110101
print_uint(x_4bit[1].item())
# > 00100011
print(qstate)
# > (tensor([4.]),
# > 'fp4',
# > tensor([ 0.0000, 0.0052, 0.6667, 1.0000, 0.3333, 0.5000, 0.1667, 0.2500,
# > 0.0000, -0.0052, -0.6667, -1.0000, -0.3333, -0.5000, -0.1667, -0.2500])])
作为输出,我们得到两个对象:一个16位数组[117,35],实际上包含我们的4个数字,和一个“状态”对象,包含缩放因子4.0和所有16个FP4数字的张量。
例如,第一个4位数字为“0111”(=7),在状态对象中我们可以看到对应的浮点值为0.25;0.25 4 = 1.0。第二个数字是“0101”(=5),结果是0.54 = 2.0。对于第三个数字,“0010”是2,0.666*4 = 2.666,接近但不等于3.0。对于4位值显然有了一些精度损失。对于最后一个值,“0011”是3,1000 *4 = 4.0。
逆向转换不需要手动操作bitsandbytes可以帮我们自动完成
x = bf.dequantize_fp4(x_4bit, qstate)
print(x)
# > tensor([1.000, 2.000, 2.666, 4.000])
4位格式也有一个有限的动态范围。例如,数组[1.0,2.0,3.0,64.0]将被转换为[0.333,0.333,0.333,64.0]。但对于规范化的数据,还是可以接受的。作为一个例子,让我们画一个FP4格式的正弦波:
import matplotlib.pyplot as plt
import numpy as np
from bitsandbytes import functional as bf
length = np.pi * 4
resolution = 256
xvals = np.arange(0, length, length / resolution)
wave = np.sin(xvals)
x_4bit, qstate = bf.quantize_fp4(torch.tensor(wave, dtype=torch.float32, device=device), blocksize=64)
dq = bf.dequantize_fp4(x_4bit, qstate)
plt.rcParams["figure.figsize"] = (14, 5)
plt.title('FP8 Sine Wave')
plt.plot(xvals, wave)
plt.plot(xvals, dq.cpu().numpy())
plt.show()
可以看到精度的损失:
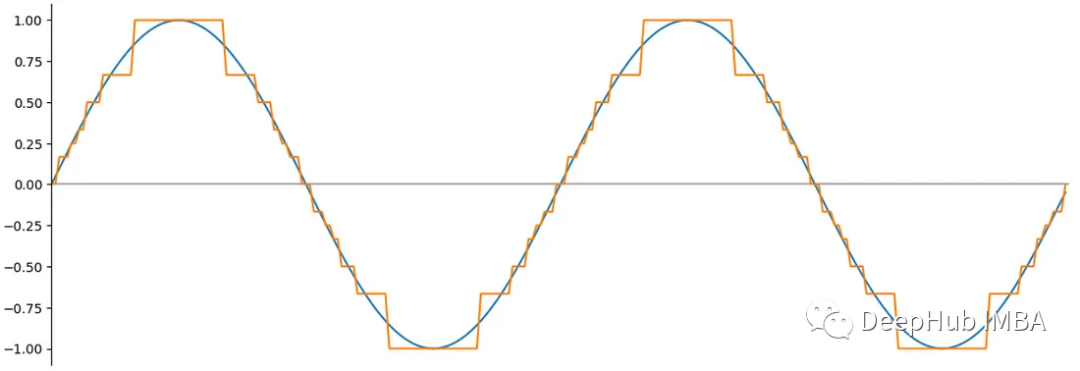
特别说明,在写这篇文章的时候,4位类型NF4只适用于CUDA;目前还不支持CPU计算。
测试
作为本文的最后一步,我们创建一个神经网络模型并对其进行测试。使用transformers库,通过将load_in_4-bit参数设置为True,就可以以4位加载预训练模型。但这并不能让我们理解它是如何工作的。所以我们将创建一个小型神经网络,训练它并以4位精度使用它。
首先,让我们创建一个神经网络模型:
import torch
import torch.nn as nn
import torch.optim as optim
from typing import Any
class NetNormal(nn.Module):
def __init__(self):
super().__init__()
self.flatten = nn.Flatten()
self.model = nn.Sequential(
nn.Linear(784, 128),
nn.ReLU(),
nn.Linear(128, 64),
nn.ReLU(),
nn.Linear(64, 10)
)
def forward(self, x):
x = self.flatten(x)
x = self.model(x)
return F.log_softmax(x, dim=1)
我们使用MNIST数据集,数据集分为6万张训练图像和1万张测试图像;可以使用参数train=True|False在DataLoader中指定选择。
from torchvision import datasets, transforms
train_loader = torch.utils.data.DataLoader(
datasets.MNIST("data", train=True, download=True,
transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
])),
batch_size=batch_size, shuffle=True)
test_loader = torch.utils.data.DataLoader(
datasets.MNIST("data", train=False, transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
])),
batch_size=batch_size, shuffle=True)
训练过程以“正常”方式进行,使用默认精度:
device = torch.device("cuda")
batch_size = 64
epochs = 4
log_interval = 500
def train(model: nn.Module, train_loader: torch.utils.data.DataLoader,
optimizer: Any, epoch: int):
""" Train the model """
model.train()
for batch_idx, (data, target) in enumerate(train_loader):
data, target = data.to(device), target.to(device)
optimizer.zero_grad()
output = model(data)
loss = F.nll_loss(output, target)
loss.backward()
optimizer.step()
if batch_idx % log_interval == 0:
print(f'Train Epoch: {epoch} [{batch_idx * len(data)}/{len(train_loader.dataset)}]\tLoss: {loss.item():.5f}')
def test(model: nn.Module, test_loader: torch.utils.data.DataLoader):
""" Test the model """
model.eval()
test_loss = 0
correct = 0
with torch.no_grad():
for data, target in test_loader:
data, target = data.to(device), target.to(device)
t_start = time.monotonic()
output = model(data)
test_loss += F.nll_loss(output, target, reduction='sum').item()
pred = output.argmax(dim=1, keepdim=True)
correct += pred.eq(target.view_as(pred)).sum().item()
test_loss /= len(test_loader.dataset)
t_diff = time.monotonic() - t_start
print(f"Test set: Average loss: {test_loss:.4f}, Accuracy: {correct}/{len(test_loader.dataset)} ({100. * correct / len(test_loader.dataset)}%)\n")
def get_size_kb(model: nn.Module):
""" Get model size in kilobytes """
size_model = 0
for param in model.parameters():
if param.data.is_floating_point():
size_model += param.numel() * torch.finfo(param.data.dtype).bits
else:
size_model += param.numel() * torch.iinfo(param.data.dtype).bits
print(f"Model size: {size_model / (8*1024)} KB")
# Train
model = NetNormal().to(device)
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.5)
for epoch in range(1, epochs + 1):
train(model, train_loader, optimizer, epoch)
test(model, test_loader)
get_size(model)
# Save
torch.save(model.state_dict(), "mnist_model.pt")
这里还有一个“get_size_kb”方法来获取以kb为单位的模型大小。
训练过程是这样的:
Train Epoch: 1 [0/60000] Loss: 2.31558
Train Epoch: 1 [32000/60000] Loss: 0.53704
Test set: Average loss: 0.2684, Accuracy: 9225/10000 (92.25%)
Train Epoch: 2 [0/60000] Loss: 0.19791
Train Epoch: 2 [32000/60000] Loss: 0.17268
Test set: Average loss: 0.1998, Accuracy: 9401/10000 (94.01%)
Train Epoch: 3 [0/60000] Loss: 0.30570
Train Epoch: 3 [32000/60000] Loss: 0.33042
Test set: Average loss: 0.1614, Accuracy: 9530/10000 (95.3%)
Train Epoch: 4 [0/60000] Loss: 0.20046
Train Epoch: 4 [32000/60000] Loss: 0.19178
Test set: Average loss: 0.1376, Accuracy: 9601/10000 (96.01%)
Model size: 427.2890625 KB
我们的简单模型准确率达到96%,神经网络大小为427 KB。
下面我们将“Linear”层替换为“Linear8bitLt”。
from bitsandbytes.nn import Linear8bitLt
class Net8Bit(nn.Module):
def __init__(self):
super().__init__()
self.flatten = nn.Flatten()
self.model = nn.Sequential(
Linear8bitLt(784, 128, has_fp16_weights=False),
nn.ReLU(),
Linear8bitLt(128, 64, has_fp16_weights=False),
nn.ReLU(),
Linear8bitLt(64, 10, has_fp16_weights=False)
)
def forward(self, x):
x = self.flatten(x)
x = self.model(x)
return F.log_softmax(x, dim=1)
device = torch.device("cuda")
# Load
model = Net8Bit()
model.load_state_dict(torch.load("mnist_model.pt"))
get_size_kb(model)
print(model.model[0].weight)
# Convert
model = model.to(device)
get_size_kb(model)
print(model.model[0].weight)
# Run
test(model, test_loader)
结果如下:
Model size: 427.2890625 KB
Parameter(Int8Params([[ 0.0071, 0.0059, 0.0146, ..., 0.0111, -0.0041, 0.0025],
...,
[-0.0131, -0.0093, -0.0016, ..., -0.0156, 0.0042, 0.0296]]))
Model size: 107.4140625 KB
Parameter(Int8Params([[ 9, 7, 19, ..., 14, -5, 3],
...,
[-21, -15, -3, ..., -25, 7, 47]], device='cuda:0',
dtype=torch.int8))
Test set: Average loss: 0.1347, Accuracy: 9600/10000 (96.0%)
原始模型以标准浮点格式加载;它的大小是一样的,权重看起来像[0.0071,0.0059,…]。模型尺寸缩小了4倍。正如我们所看到的,权重值在相同的范围内,因此转换很容易-在测试运行期间,根本没有准确性损失!
再继续4bit的版本:
from bitsandbytes.nn import LinearFP4, LinearNF4
class Net4Bit(nn.Module):
def __init__(self):
super().__init__()
self.flatten = nn.Flatten()
self.model = nn.Sequential(
LinearFP4(784, 128),
nn.ReLU(),
LinearFP4(128, 64),
nn.ReLU(),
LinearFP4(64, 10)
)
def forward(self, x):
x = self.flatten(x)
x = self.model(x)
return F.log_softmax(x, dim=1)
# Load
model = Net4Bit()
model.load_state_dict(torch.load("mnist_model.pt"))
get_model_size(model)
print(model.model[2].weight)
# Convert
model = model.to(device)
get_model_size(model)
print(model.model[2].weight)
# Run
test(model, test_loader)
输出如下所示:
Model size: 427.2890625 KB
Parameter(Params4bit([[ 0.0916, -0.0453, 0.0891, ..., 0.0430, -0.1094, -0.0751],
...,
[-0.0079, -0.1021, -0.0094, ..., -0.0124, 0.0889, 0.0048]]))
Model size: 54.1015625 KB
Parameter(Params4bit([[ 95], [ 81], [109],
...,
[ 34], [ 46], [ 33]], device='cuda:0', dtype=torch.uint8))
Test set: Average loss: 0.1414, Accuracy: 9579/10000 (95.79%)
模型大小减少了8倍,从427 KB减少到54 KB,但准确率下降1%。这怎么可能?至少对这个模型来说,答案很简单:
- 权重或多或少是均匀分布的,并且精度损失不是太大。
- 神经网络使用Softmax作为输出,最大值的索引决定了实际结果。所以对于寻找最大索引,值本身并不重要。例如,当其他值为0.1或0.2时,该值为0.8或0.9没有任何区别!
我们从测试数据集加载数字并检查模型输出。
dataset = datasets.MNIST('data', train=False, transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
]))
np.set_printoptions(precision=3, suppress=True) # No scientific notation
data_in = dataset[4][0]
for x in range(28):
for y in range(28):
print(f"{data_in[0][x][y]: .1f}", end=" ")
print()
打印输出显示了我们想要预测的数字:

让我们看看“标准”模型将返回什么:
# Suppress scientific notation
np.set_printoptions(precision=2, suppress=True)
# Predict
with torch.no_grad():
output = model(data_in.to(device))
print(output[0].cpu().numpy())
ind = output.argmax(dim=1, keepdim=True)[0].cpu().item()
print("Result:", ind)
# > [ -8.27 -13.89 -6.89 -11.13 -0.03 -8.09 -7.46 -7.6 -6.43 -3.77]
# > Result: 4
最大元素位于第5个位置(numpy数组中的元素从0开始编号),对应于数字“4”。
这是 8-bit:模型的输出:
# > [ -9.09 -12.66 -8.42 -12.2 -0.01 -9.25 -8.29 -7.26 -8.36 -4.45]
# > Result: 4
4-bit的如下:
# > [ -8.56 -12.12 -7.52 -12.1 -0.01 -8.94 -7.84 -7.41 -7.31 -4.45]
# > Result: 4
可以看到实际输出值略有不同,但最大索引是保持不变的。
总结
在本文中,我们测试了16位、8位和4位浮点数的不同方案,创建了一个神经网络,并能够以8位和4位精度运行它。通过将精度从标准浮点数降低到4位浮点数,内存占用减少了8倍,但精度损失最小。
就像我们昨天的文章中提到的,即使是4位也已经不是极限了;在GPTQ论文中,提到了将权重量化为2甚至3元(1.5比特!)。还有可以对不同层应用不同量化的ExLlamaV2。
作者:Dmitrii Eliuseev