时序分析 49 -- 贝叶斯时序预测（一）

贝叶斯时序预测（一）

时序预测在统计分析和机器学习领域一直都是一个比较重要的话题。在本系列前面的文章中我们介绍了诸如ARIMA系列方法，Holt-Winter指数平滑模型等多种常用方法，实际上这些看似不同的模型和方法之间都具有千丝万缕的联系，包括我们一直没有涉及的最复杂的模型LSTM(Long Short Term Memory)。在实际的时序数据分析工作中，你会发现在通常境况下简单模型都比复杂模型更为有效。本文开始讨论另一套时序预测体系：Bayes 时序预测方法。这套方法的背后原理可以很简单，但也可以很深，我们不如从一个例子开始，先积累一些直觉和经验，后续系列会展开理论部分的讨论。
贝叶斯时序预测通常不会预测时序点，而是给出时序点的分布，但如果希望预测时序点，你可以简单取该分布的均值或者中位数。

贝叶斯定理回顾

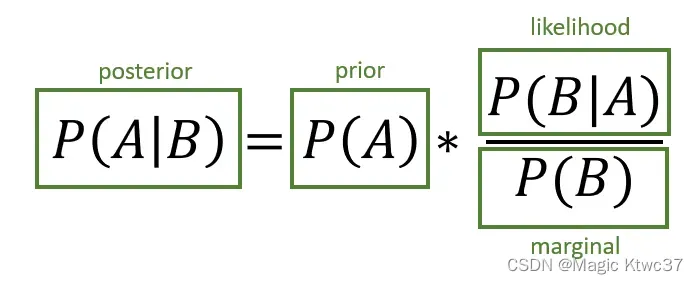
上图展示了贝叶斯定理的基本结构，这个定理可以认为是机器学习领域最重要的定理了，个人认为没有之一。

让我们来简单回顾一下这个定理的核心内容，

•                                          P                               (                               A                               )                                      P(A)                        P(A) ,是事件                                             A                                      A                        A的先验概率，可以理解为在没有任何具体的数据支持下，我们对事件                                             A                                      A                        A发生的概率的直觉，也可称为prior belief(先验信念)。先验信念表示了我们对事件                                             A                                      A                        A发生概率的主观理解。

•                                          P                               (                               B                               )                                      P(B)                        P(B)，是事件                                             B                                      B                        B的概率，在贝叶斯定理中一般称为边缘概率（marginal)。

•                                          P                               (                               A                               ∣                               B                               )                                      P(A|B)                        P(A∣B)，是当事件                                             B                                      B                        B发生时事件                                             A                                      A                        A发生的条件概率，在贝叶斯定理中称为后验概率(posterior)。

•                                          P                               (                               B                               ∣                               A                               )                                      P(B|A)                        P(B∣A)，适当事件                                             A                                      A                        A发生时事件                                             B                                      B                        B发生的条件概率，在贝叶斯定理中称为似然性(likelihood)。    我们可以这样理解贝叶斯公式：首先定义一个我们对某个事件的主观理解的先验分布，然后通过数据和事实我们得到似然性，条件于边缘概率后得到后延概率。 通俗来说，我们对一个事情有一个信念，当我们看到与这个事情有关的数据和事实后，我们会更新这个信念。举个例子来说，例如我们有一个硬币，我们相信随机抛这个硬币，落地时正面朝上的概率时1/2。但事实上这个硬币由于制造工艺的随机性导致其正面朝上的概率为2/3，当我们做抛硬币实验时，随着我们观察到正面朝上的概率大于1/2，我们对这件事情的信念会随着事实而变化。    关于贝叶斯定理，日后我们还会做进一步讨论，尝试从其他维度更深一步理解这个重要定理。

贝叶斯时序预测

贝叶斯时序预测模型的一种最常用的方法称为：DGLM(Dynamic Generalized Linear Model)，既动态泛化线性模型，这里

• 动态，模型系数会随时间变化而变化。

• 泛化，过观察的分布可以是多种分布，例如正态分布、泊松分布、伯努利分布、二项式分布等。

• 线性，预测值既系数与预测变量的乘积的线性组合。此模型的关键要素为：

      λ 
     
    
      t 
     
    
   
     = 
    
    
    
      F 
     
    
      t 
     
    
    
    
      θ 
     
    
      t 
     
    
   
    \lambda_t=F_t \theta_t 
   

  λt​=Ft​θt​

•                                                      λ                                  t                                                 \lambda_t                        λt​是线性预测变量

•                                                      θ                                  r                                                 \theta_r                        θr​是状态向量，DGLM的系数融入到状态向量中，实际建模中此向量由一些组件组成，例如趋势、回归性、季节、节假日和特殊事件等。

•                                                      F                                  t                                                 F_t                        Ft​是回归向量    这些变量都会有对应的折现因子，折现因子是在构建模型中由我们设定的，它表示我们给当先信息和历史信息所分配的权重。

Python 简单例子

读入数据和所需包

import pandas as pd
import matplotlib.pyplot as plt
import matplotlib.dates as dt
from pybats.analysis import analysis
from pybats.point_forecast import median
df = pd.read_csv('airpassengers.csv')# Changing the datatype
df["Month"]= pd.to_datetime(df['Month'],format='%Y-%m')# Setting the Date as index
df = df.set_index('Month')
Y = df['#Passengers'].values

pybats为贝叶斯时许预测提供了很多参数，我们先来简单看一下

k =1# 向前预测一步
forecast_start =0# 预测从时间零点开始
forecast_end =len(df)-1# 预测在数据最后结束
mod, samples = analysis(
    Y,
    family="poisson",# 使用泊松分布
    forecast_start=forecast_start,
    forecast_end=forecast_end,
    k=k,
    nsamps=100,# 每个月取一百个样本
    prior_length=6,# 取6个点来定义先验分布
    rho=.9,# 随机效用扩展
    deltrend=0.5,# 趋势折现因子
    delregn=0.9# 回归折现因子)
forecast = median(samples)# 预测

参数解释：

• family=”possion“: 我们可尝试使用泊松分布对正整数建模；使用normal对连续实数；使用bernoulli对0-1;使用binomial对bernoulli的加总和。
• nsamps=100：定义样本的数量，通过此样本可得到信任区间（credibale interval)和点估计（point estimate)
• prior_length=6：构造先验分布的点的数量，这个数值越大说明使用时序开始数据来建模先验分布的观测值越多
• rho=.9：随机效用扩展，这个参数增加了预测的波动

# Plotting
fig, ax = plt.subplots(1,1, figsize=(8,6))   
ax = plot_data_forecast(fig, ax, Y, forecast, samples,
                        dates=df.index)
ax = ax_style(ax, ylabel='Sales', xlabel='Time',
              legend=['Forecast','Passengers','Credible Interval'])

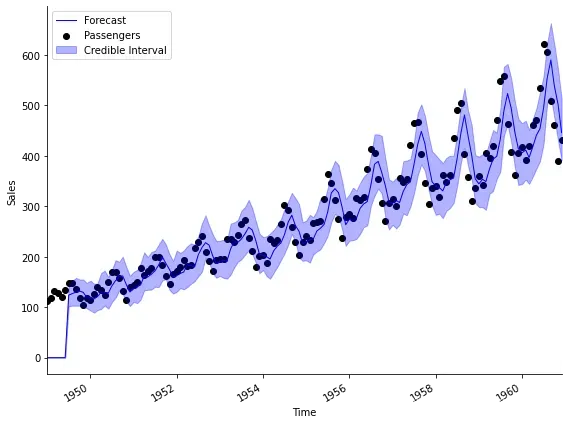
注意，上图中开始的水平线表明了建立先验分布所使用的月数，所以这里没有开始预测。 可以使用analysis函数来评估预测效果和对数据的拟合程度。

就这份数据而言，看上去拟合得不错，但我们需要知道

• 这个例子实际上不是预测，只能算是”事后诸葛亮“
• 这个数据集实际上非常好，有比较强的趋势和季节成分 PyBATS还有很多其他功能我们没有在这里演示，例如：
• 增加节假日和特殊事件
• 深一步使用DGLM
• 使用隐含因子(latent factors)，例如增加机票的平均价格来优化乘客人数的预测过程。

这只是个非常简单且不太完整的例子，如开头所言，这个例子只能给我们一些感性认识，后续笔者会分享更多关于这个主题的深层次的讨论和实践。