目录
前言
本文属于 线性回归算法【AIoT阶段三】(尚未更新),这里截取自其中一段内容,方便读者理解和根据需求快速阅读。
线性回归是机器学习中有监督机器学习下的一种算法。 回归问题主要关注的是因变量(需要预测的值,可以是一个也可以是多个)和一个或多个数值型的自变量(预测变量)之间的关系。
需要预测的值:即目标变量,target,y,连续值预测变量。
影响目标变量的因素:
X
1
X_1
X1…
X
n
X_n
Xn,可以是连续值也可以是离散值。
因变量和自变量之间的关系:即模型,model,是我们要求解的。
1.基本概念
1.1 连续值
🚩连续值就是连续的一连串数字,是可以无限细分下去的一段,比如我们的身高,你可以说你身高在
175
175
175至
185
185
185,继续细分下去也是可以的,你甚至可以说你的身高在
175.003
175.003
175.003 至
182.231
182.231
182.231 甚至继续下分下去也没可以的,这就被称为是连续值。

1.2 离散值
🚩离散值就是单个孤立的点,比如我国共计34个省级行政区,我们绝不可以说成我国共计34.3个省级行政区,或者是33.6个省级行政区,必须是 34 整个,这就是离散值。
1.3 简单线性回归
🚩什么是算法?研究算法说白了还是在研究公式,简单线性回归属于一个算法,它所对应的公式:
y
=
w
x
+
b
y = wx + b
y=wx+b,这个公式中,
y
y
y 是目标变量即未来要预测的值,
x
x
x 是影响
y
y
y 的因素,
w
,
b
w,b
w,b 是公式上的参数即要求的模型。其实
b
b
b 就是咱们的截距,
w
w
w 就是斜率嘛! 所以很明显如果模型求出来了,未来影响
y
y
y 值的未知数就是一个
x
x
x 值,也可以说影响
y
y
y 值 的因素只有一个,所以这是就叫**简单**线性回归的原因,如下图所表示的直线,就是一个简单线性回归的意思:
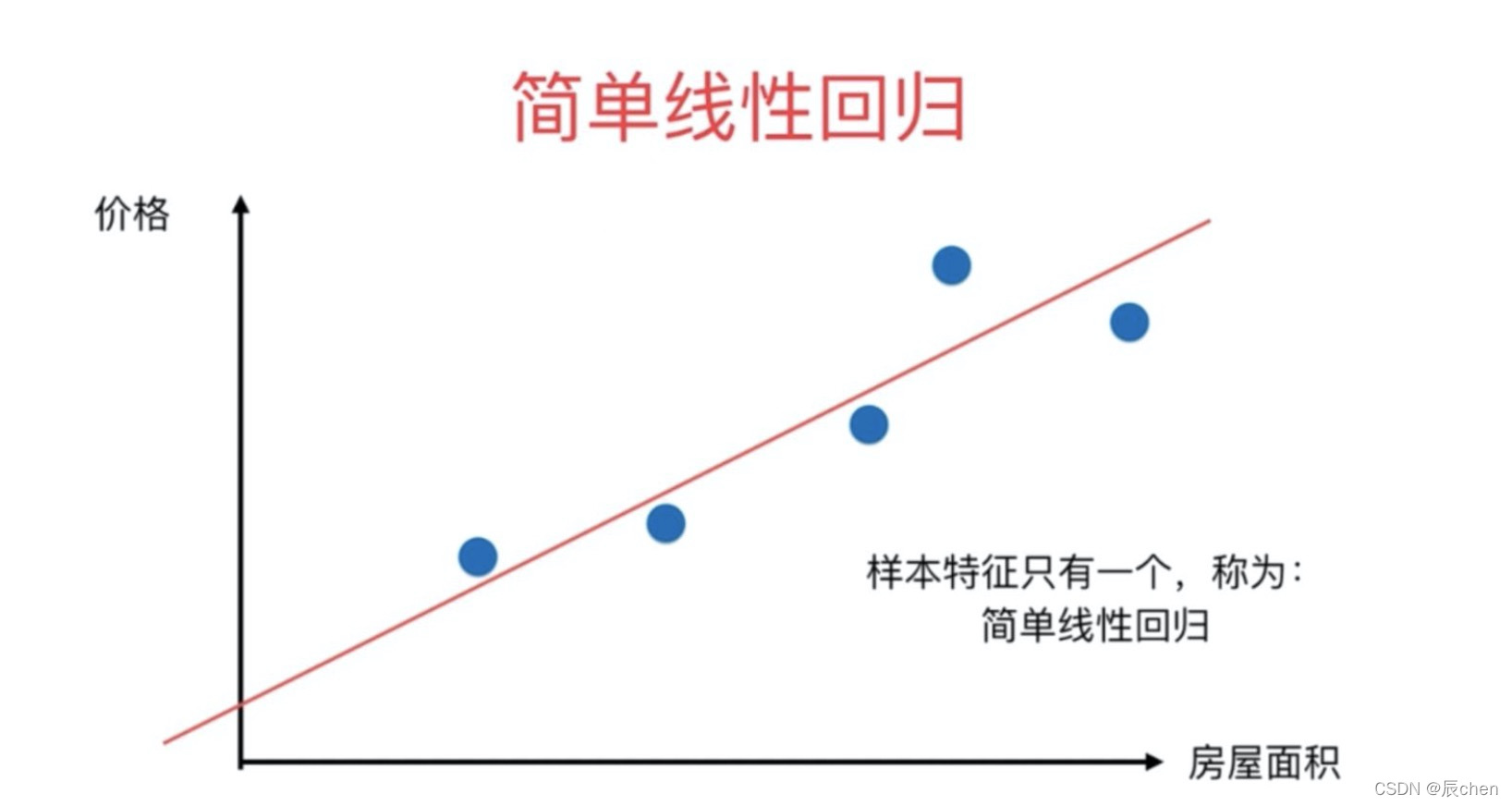
1.4 基本名词的定义
A
c
t
u
a
l
v
a
l
u
e
Actual value
Actualvalue:**真实值**,一般使用
y
y
y 表示。
P
r
e
d
i
c
t
e
d
v
a
l
u
e
Predicted value
Predictedvalue:**预测值**,是把已知的
x
x
x 带入到公式里面和**猜**出来的参数
w
,
b
w,b
w,b 计算得到的,一般使用
y
^
\hat{y}
y^ 表示。
E
r
r
o
r
Error
Error:**误差**,预测值和真实值的差距,一般使用
ε
\varepsilon
ε 表示
最优解:尽可能的找到一个模型使得整体的误差最小,整体的误差通常叫做损失
L
o
s
s
Loss
Loss
L
o
s
s
Loss
Loss:整体的误差,
L
o
s
s
Loss
Loss 通过损失函数
L
o
s
s
Loss
Loss
f
u
n
c
t
i
o
n
function
function 计算得到。
1.5 多元线性回归
🚩多元线性回归无非就是比简单线性回归变得: 多元,所谓多元,就是在某些情况下,影响结果
y
y
y 的因素不止有一个,比如我们在预测股票的时候,国家的政策起到影响作用,国民的经济也是影响因素,甚至他国的经济政策也会影响到我们,等等等等有诸多原因,为此,仅仅一个变量
x
x
x 就显得不够用了,这时,我们的
x
x
x 就从
1
1
1 个变成了
n
n
n 个:
X
1
X_1
X1…
X
n
X_n
Xn, 同时简单线性回归的公式也就不在适用了。**多元线性回归**公式如下:
y
^
=
w
1
X
1
+
w
2
X
2
+
…
…
+
w
n
X
n
+
b
\hat{y} = w_1X_1 + w_2X_2 + …… + w_nX_n + b
y^=w1X1+w2X2+……+wnXn+b
b是截距,也可以使用
w
0
w_0
w0来表示
y
^
=
w
1
X
1
+
w
2
X
2
+
…
…
+
w
n
X
n
+
w
0
\hat{y} = w_1X_1 + w_2X_2 + …… + w_nX_n + w_0
y^=w1X1+w2X2+……+wnXn+w0
y
^
=
w
1
X
1
+
w
2
X
2
+
…
…
+
w
n
X
n
+
w
0
∗
1
\hat{y} = w_1X_1 + w_2X_2 + …… + w_nX_n + w_0 * 1
y^=w1X1+w2X2+……+wnXn+w0∗1
使用向量来表示,
X
X
X表示所有的变量,是一维向量;
w
w
w 表示所有的系数(包含
w
0
w_0
w0),是一维向量,根据向量乘法规律,可以这么写:
y
^
=
W
T
X
\hat{y} = W^TX
y^=WTX
y
^
=
∣
w
1
w
2
.
.
.
w
n
w
0
∣
∗
∣
X
1
X
2
.
.
.
X
n
1
∣
\hat{y} =\left|\begin{matrix}w_1 \\ w_2 \\ ... \\ w_n \\ w_0 \end{matrix}\right| *\left|\begin{matrix}X_1 & X_2 & ... & X_n & 1 \end{matrix}\right|
y^=∣∣∣∣∣∣∣∣∣∣w1w2...wnw0∣∣∣∣∣∣∣∣∣∣∗∣∣X1X2...Xn1∣∣
2.正规方程
2.1 最小二乘法的矩阵表示
🚩最小二乘法可以将误差方程转化为有确定解的代数方程组(其方程式数目正好等于未知数的个数),从而可求解出这些未知参数。这个有确定解的代数方程组称为最小二乘法估计的正规方程。公式如下:
θ
=
(
X
T
X
)
−
1
X
T
y
\theta = (X^TX)^{-1}X^Ty
θ=(XTX)−1XTy 或者
W
=
(
X
T
X
)
−
1
X
T
y
W = (X^TX)^{-1}X^Ty
W=(XTX)−1XTy ,其中的
W
、
θ
W、\theta
W、θ 即使方程的解!
公式是如何推导的在 **2.4 推导正规方程
θ
\theta
θ 的解** 中进行详细讲解。
最小二乘法公式如下:
J
(
θ
)
=
1
2
∑
i
=
0
n
(
h
θ
(
x
i
)
−
y
i
)
2
J(\theta) = \frac{1}{2}\sum\limits_{i = 0}^n(h_{\theta}(x_i) - y_i)^2
J(θ)=21i=0∑n(hθ(xi)−yi)2
使用矩阵表示:
J
(
θ
)
=
1
2
∑
i
=
0
n
(
h
θ
(
x
i
)
−
y
)
(
h
θ
(
x
i
)
−
y
)
J(\theta) = \frac{1}{2}\sum\limits_{i = 0}^n(h_{\theta}(x_i) - y)(h_{\theta}(x_i) - y)
J(θ)=21i=0∑n(hθ(xi)−y)(hθ(xi)−y)
J
(
θ
)
=
1
2
(
X
θ
−
y
)
T
(
X
θ
−
y
)
J(\theta) = \frac{1}{2}(X\theta - y)^T(X\theta - y)
J(θ)=21(Xθ−y)T(Xθ−y)
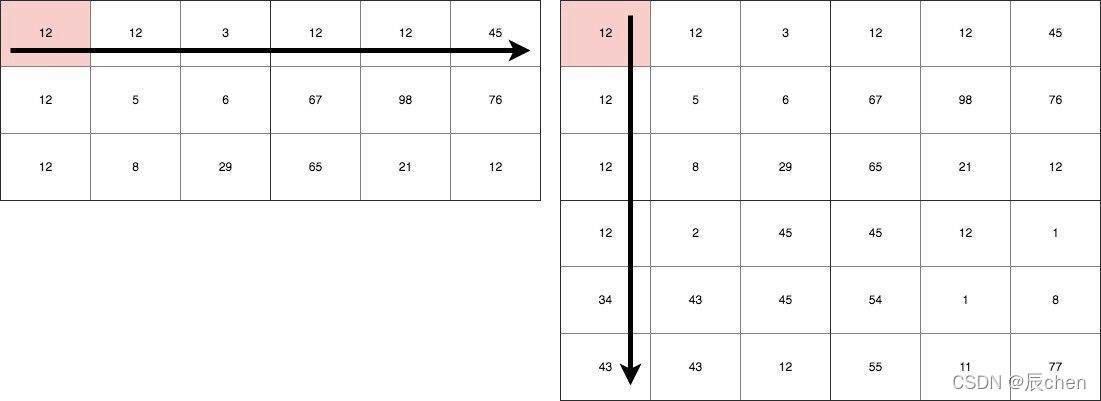
之所以要使用转置
T
T
T,是因为,矩阵运算规律是:矩阵
A
A
A 的一行乘以矩阵
B
B
B 的一列!
2.2 多元一次方程举例
2.2.1 二元一次方程
{
x
+
y
=
14
2
x
−
y
=
10
\begin{cases} x + y=14\\ 2x - y = 10\\ \end{cases}
{x+y=142x−y=10
import numpy as np
import matplotlib.pyplot as plt
X = np.array([[1,1],[2,-1]])
y = np.array([14,10])# linalg 线性代数,solve计算线性回归问题
np.linalg.solve(X, y)

我们来根据上述中的正规方程来计算一下:
W
=
(
X
T
X
)
−
1
X
T
y
W = (X^TX)^{-1}X^Ty
W=(XTX)−1XTy:
A = X.T.dot(X)
B = np.linalg.inv(A)## 求逆矩阵
C = B.dot(X.T)
C.dot(Y)
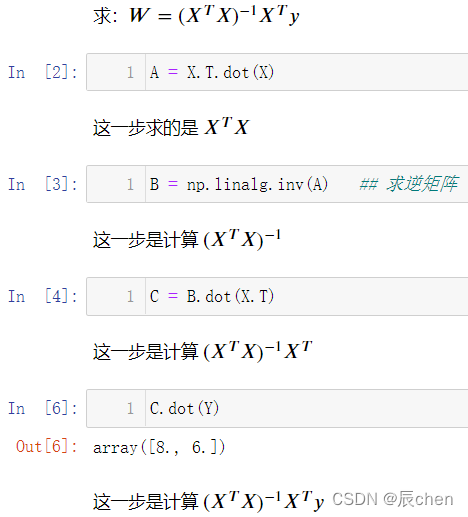
可以发现,我们使用正规方程可以同样有效的进行计算,我们再来举几个例子
2.2.2 三元一次方程
{
x
−
y
+
z
=
100
2
x
+
y
−
z
=
80
3
x
−
2
y
+
6
z
=
256
\begin{cases} x - y + z = 100\\ 2x + y -z = 80\\ 3x - 2y + 6z = 256\\ \end{cases}
⎩⎪⎨⎪⎧x−y+z=1002x+y−z=803x−2y+6z=256
import numpy as np
import matplotlib.pyplot as plt
X = np.array([[1,-1,1],[2,1,-1],[3,-2,6]])
y = np.array([100,80,256])# 根据正规方程进行计算:
W = np.linalg.inv(X.T.dot(X)).dot(X.T).dot(y)
W

2.2.3 八元一次方程
{
14
x
2
+
8
x
3
+
5
x
5
+
−
2
x
6
+
9
x
7
+
−
3
x
8
=
339
−
4
x
1
+
10
x
2
+
6
x
3
+
4
x
4
+
−
14
x
5
+
−
2
x
6
+
−
14
x
7
+
8
x
8
=
−
114
−
1
x
1
+
−
6
x
2
+
5
x
3
+
−
12
x
4
+
3
x
5
+
−
3
x
6
+
2
x
7
+
−
2
x
8
=
30
5
x
1
+
−
2
x
2
+
3
x
3
+
10
x
4
+
5
x
5
+
11
x
6
+
4
x
7
+
−
8
x
8
=
126
−
15
x
1
+
−
15
x
2
+
−
8
x
3
+
−
15
x
4
+
7
x
5
+
−
4
x
6
+
−
12
x
7
+
2
x
8
=
−
395
11
x
1
+
−
10
x
2
+
−
2
x
3
+
4
x
4
+
3
x
5
+
−
9
x
6
+
−
6
x
7
+
7
x
8
=
−
87
−
14
x
1
+
4
x
3
+
−
3
x
4
+
5
x
5
+
10
x
6
+
13
x
7
+
7
x
8
=
422
−
3
x
1
+
−
7
x
2
+
−
2
x
3
+
−
8
x
4
+
−
6
x
6
+
−
5
x
7
+
−
9
x
8
=
−
309
\begin{cases}&14x_2 + 8x_3 + 5x_5 + -2x_6 + 9x_7 + -3x_8 = 339\\&-4x_1 + 10x_2 + 6x_3 + 4x_4 + -14x_5 + -2x_6 + -14x_7 + 8x_8 = -114\\&-1x_1 + -6x_2 + 5x_3 + -12x_4 + 3x_5 + -3x_6 + 2x_7 + -2x_8 = 30\\&5x_1 + -2x_2 + 3x_3 + 10x_4 + 5x_5 + 11x_6 + 4x_7 + -8x_8 = 126\\&-15x_1 + -15x_2 + -8x_3 + -15x_4 + 7x_5 + -4x_6 + -12x_7 + 2x_8 = -395\\&11x_1 + -10x_2 + -2x_3 + 4x_4 + 3x_5 + -9x_6 + -6x_7 + 7x_8 = -87\\&-14x_1 + 4x_3 + -3x_4 + 5x_5 + 10x_6 + 13x_7 + 7x_8 = 422\\&-3x_1 + -7x_2 + -2x_3 + -8x_4 + -6x_6 + -5x_7 + -9x_8 = -309\end{cases}
⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧14x2+8x3+5x5+−2x6+9x7+−3x8=339−4x1+10x2+6x3+4x4+−14x5+−2x6+−14x7+8x8=−114−1x1+−6x2+5x3+−12x4+3x5+−3x6+2x7+−2x8=305x1+−2x2+3x3+10x4+5x5+11x6+4x7+−8x8=126−15x1+−15x2+−8x3+−15x4+7x5+−4x6+−12x7+2x8=−39511x1+−10x2+−2x3+4x4+3x5+−9x6+−6x7+7x8=−87−14x1+4x3+−3x4+5x5+10x6+13x7+7x8=422−3x1+−7x2+−2x3+−8x4+−6x6+−5x7+−9x8=−309
import numpy as np
import matplotlib.pyplot as plt
X = np.array([[0,14,8,0,5,-2,9,-3],[-4,10,6,4,-14,-2,-14,8],[-1,-6,5,-12,3,-3,2,-2],[5,-2,3,10,5,11,4,-8],[-15,-15,-8,-15,7,-4,-12,2],[11,-10,-2,4,3,-9,-6,7],[-14,0,4,-3,5,10,13,7],[-3,-7,-2,-8,0,-6,-5,-9]])
y = np.array([339,-114,30,126,-395,-87,422,-309])# 根据正规方程进行计算:
W = np.linalg.inv(X.T.dot(X)).dot(X.T).dot(y)
W

2.2.4
s
k
l
e
a
r
n
sklearn
sklearn 算法使用
🚩没有安装这个包的同学在命令行中输入:
pip install sklearn
即可,如果你看过博文:最详细的Anaconda Installers 的安装【numpy,jupyter】(图+文) 或者 数据分析三剑客【AIoT阶段一(下)】(十万字博文 保姆级讲解),那么这一步可省略:在安装
j
u
p
y
t
e
r
jupyter
jupyter 的时候已经安装完成,如果你没有设置以 **清华源** 为地址进行下载会很慢,配置默认下载从 **清华源** 下载可见博文:matplotlib的安装教程以及简单调用
下面还是来计算我们上述的八元一次方程组:
# linear:线性 model:模型、算法# LinearRegression: 线性回归from sklearn.linear_model import LinearRegression
import numpy as np
import matplotlib.pyplot as plt
model = LinearRegression()
X = np.array([[0,14,8,0,5,-2,9,-3],[-4,10,6,4,-14,-2,-14,8],[-1,-6,5,-12,3,-3,2,-2],[5,-2,3,10,5,11,4,-8],[-15,-15,-8,-15,7,-4,-12,2],[11,-10,-2,4,3,-9,-6,7],[-14,0,4,-3,5,10,13,7],[-3,-7,-2,-8,0,-6,-5,-9]])
y = np.array([339,-114,30,126,-395,-87,422,-309])# X:数据 y:目标值
model.fit(X, y)# coef_ : 结果、返回值# 就是指方程的解、W、系数、斜率
model.coef_
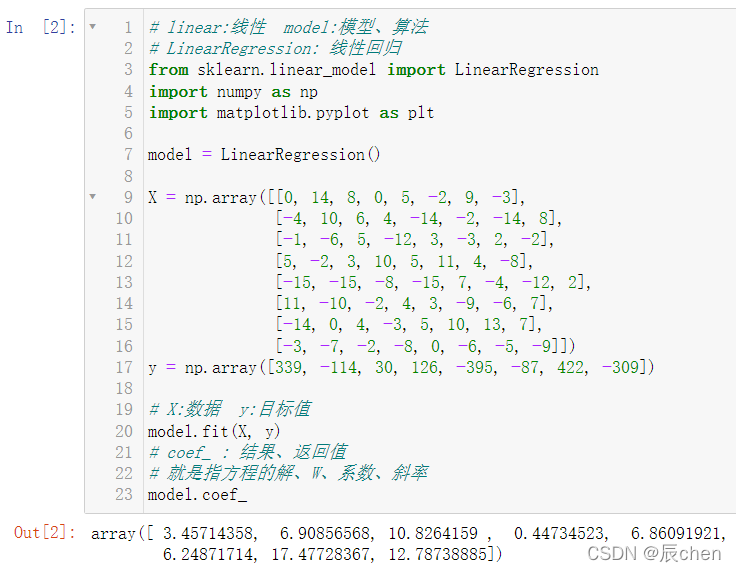
我们发现,运行结果和我们用正规方程计算出来的不一样,这是因为在代码:
model = LinearRegression()
有一个参数叫做:
intercept_
,意为截距,即我们调用
s
k
l
e
a
r
n
sklearn
sklearn 自动计算了截距:
# 默认计算截距
model.intercept_

但其实我们的八元一次方程是没有截距的,故我们在代码改为如下即可:
model = LinearRegression(fit_intercept =False)
完整代码:
# linear:线性 model:模型、算法# LinearRegression: 线性回归from sklearn.linear_model import LinearRegression
import numpy as np
import matplotlib.pyplot as plt
model = LinearRegression(fit_intercept =False)
X = np.array([[0,14,8,0,5,-2,9,-3],[-4,10,6,4,-14,-2,-14,8],[-1,-6,5,-12,3,-3,2,-2],[5,-2,3,10,5,11,4,-8],[-15,-15,-8,-15,7,-4,-12,2],[11,-10,-2,4,3,-9,-6,7],[-14,0,4,-3,5,10,13,7],[-3,-7,-2,-8,0,-6,-5,-9]])
y = np.array([339,-114,30,126,-395,-87,422,-309])# X:数据 y:目标值
model.fit(X, y)# coef_ : 结果、返回值# 就是指方程的解、W、系数、斜率
model.coef_
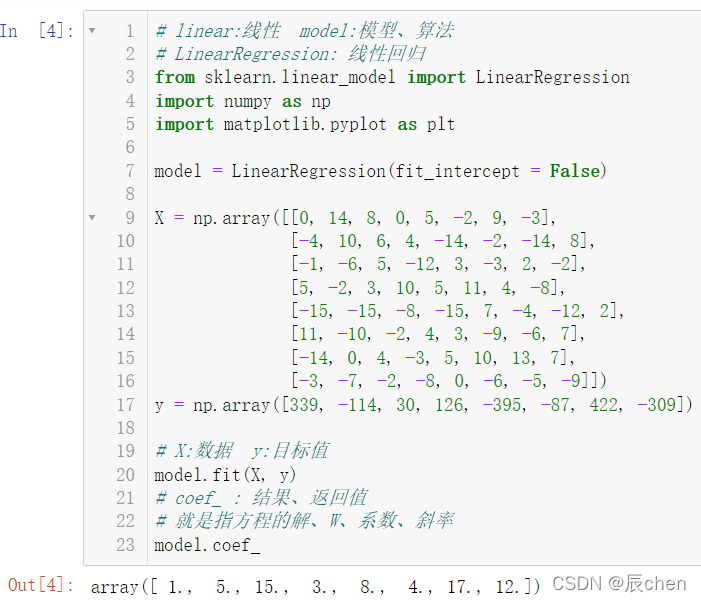
此时我们再来计算一下截距:
model.intercept_

2.2.5 带截距的线性方程
2.2.5.1 增加截距
12
12
12
🚩上述八元一次方程的解其实就是:
f
(
x
)
=
x
1
+
5
x
2
+
15
x
3
+
3
x
4
+
8
x
5
+
4
x
6
+
17
x
7
+
12
x
8
{f(x)=x_1+5x_2+15x_3+3x_4+8x_5+4x_6+17x_7+12x_8}
f(x)=x1+5x2+15x3+3x4+8x5+4x6+17x7+12x8
现在我们不妨让上式加上一个任意常数,比如
12
12
12,
那么方程的解就变成了:
f
(
x
)
=
x
1
+
5
x
2
+
15
x
3
+
3
x
4
+
8
x
5
+
4
x
6
+
17
x
7
+
12
x
8
+
12
{f(x)=x_1+5x_2+15x_3+3x_4+8x_5+4x_6+17x_7+12x_8+12}
f(x)=x1+5x2+15x3+3x4+8x5+4x6+17x7+12x8+12
那么显然我们的
y
y
y 要发生改变,即对于
y
y
y 中的每一个元素都要加上
12
12
12:这时,因为有了截距,我们就需要让
intercept
置为
True
:
y = y +12
display(y)
model = LinearRegression(fit_intercept =True)# fit:健身,训练;特质算法、模型训练,拟合# 数据 X 和 y 之间存在规律,拟合出来,找到规律
model.fit(X, y)
b_ = model.intercept_
print('截距是:', b_)
w_ = model.coef_
print('斜率是:', w_)print('方程的解为:', X.dot(w_)+ b_)
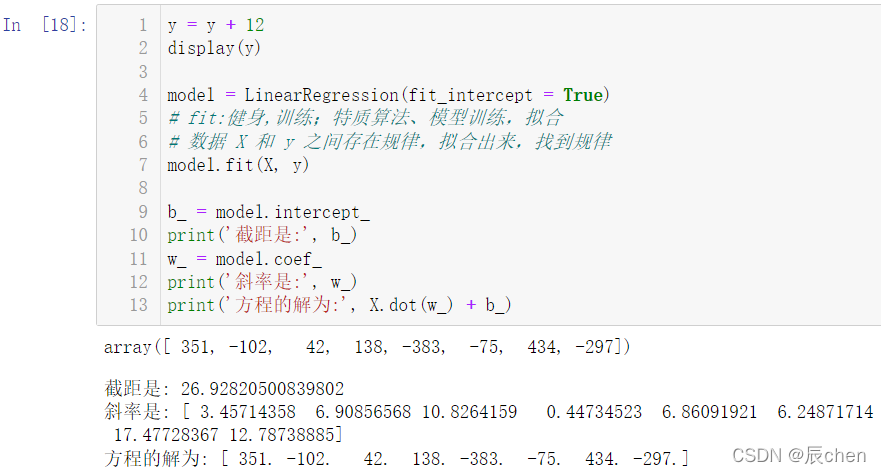
我们可以看出,求出来的截距虽然不是我们加上的
12
12
12,斜率也不是我们之前求过的解,但是这两个结合起来确确实实是方程的解。

求出的不是我们期望的结果,但是是符合题意的结果,这是因为,一旦我们规定了
fit_intercept = True
,那么在计算机进行解方程的时候,就不会使用正规方程去进行运算
2.2.5.2 修改数据
X
X
X
🚩我们根据 1.5 多元线性回归 所讲过的对
X
X
X 进行修改:即给
X
X
X 所代表的矩阵中在最后一列的位置增加一个
1
1
1:
X = np.concatenate([X, np.full(shape =(8,1), fill_value =1)], axis =1)
display(X, y)

那么这个数据,相比较与最开始的八元一次方程,我们让
X
X
X 增加了一列,
y
y
y 增加了
12
12
12,那么接下来进行正规方程的计算:
model = LinearRegression(fit_intercept =False)
model.fit(X, y)
display(model.coef_, model.intercept_)

我们发现和我们的预期还是相差甚远,我们期望的是计算截距为
12
12
12,斜率为:
a
r
r
a
y
(
[
1.
,
5.
,
15.
,
3.
,
8.
,
4.
,
17.
,
12.
]
)
array([ 1., 5., 15., 3., 8., 4., 17., 12.])
array([1.,5.,15.,3.,8.,4.,17.,12.]),但是为什么出现了这么大的误差呢?我们再来用
W
=
(
X
T
X
)
−
1
X
T
y
W = (X^TX)^{-1}X^Ty
W=(XTX)−1XTy 计算一下正规方程:
W = np.linalg.inv(X.T.dot(X)).dot(X.T).dot(y)
W

可以看出即使是使用我们推导出的正规方程也和我们期待的相差甚远,我们来查看一下此时的
X
X
X
X.shape

这意味着,我们有八个方程,但是我们有九个未知数,显然,对于这样的一个方程组,我们并非只有一组解,而是有无穷多组解,这也是我们产生偏差的原因。
你或许有疑问,既然有无穷多组解,那么每次运行的结果应该是不同的,为什么对于正规方程每次运行的结果确实相同的:这是因为算法会默认给我们算出一个 最优解,所以我们要有唯一解,就需要我们人为的添加一个方程:
# w就是标准的解
w = np.array([1.,5.,15.,3.,8.,4.,17.,12.])# 造一个方程出来
X9 = np.random.randint(-15,15, size =8)
display(X9)

接下来对于这个方程我们按照增加
12
12
12 截距和修改数据的方法来改变这个方程:
# 上面的8个方程,都有截距12,第九个方程也是如此
X9.dot(w)+12
y = np.concatenate([y,[X9.dot(w)+12]])
y
X9 = np.concatenate([X9,[1]])
X9
X = np.concatenate([X,[X9]])
X
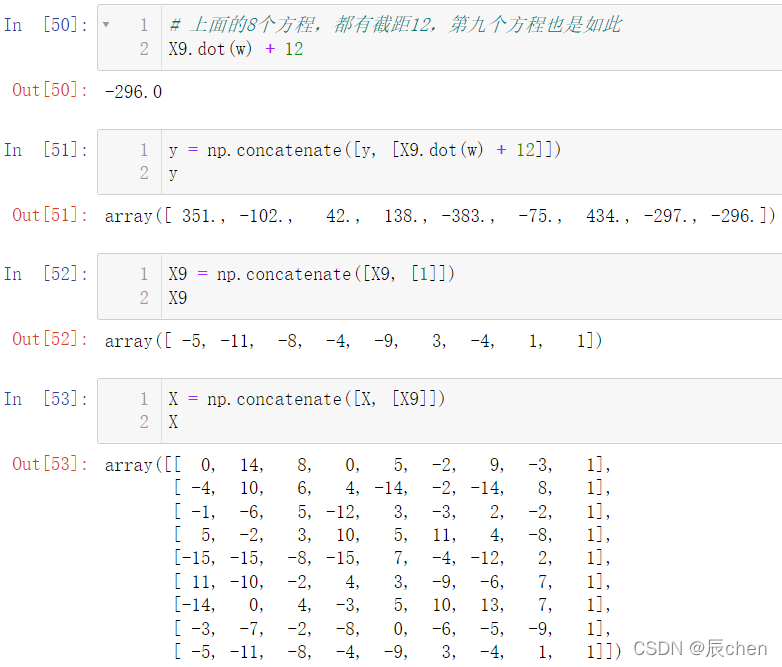
以上操作后我们就处理好了
X
X
X 和
y
y
y,那么接下来,就是见证奇迹的时刻:
# 计算正规方程
np.linalg.inv(X.T.dot(X)).dot(X.T).dot(y)

使用线性回归:
model = LinearRegression(fit_intercept =False)
model.fit(X, y)
display(model.coef_)

那么这还是有些区别,因为我们想要的是截距以及斜率,但是此时我们只有斜率,故我们可以把
fit_intercept
设置为
True
:
model = LinearRegression(fit_intercept =True)
model.fit(X, y)
display(model.coef_, model.intercept_)

截距是不是离我们的真实值特别靠近啦,此时我们只需要进行四舍五入即可,对于值为
0
0
0 的解,即我们自定义出来的
X
9
X_9
X9,
0
0
0 代表其没有权重,故我们可以舍去它
model = LinearRegression(fit_intercept =True)
model.fit(X[:,:-1], y)
display(model.coef_, model.intercept_.round())

芜湖!大功告成!!!
2.3 矩阵转置公式与求导公式
转置公式如下:
( m A ) T = m A T (mA)^T = mA^T (mA)T=mAT,其中m是常数( A + B ) T = A T + B T (A + B)^T = A^T + B^T (A+B)T=AT+BT( A B ) T = B T A T (AB)^T = B^TA^T (AB)T=BTAT( A T ) T = A (A^T)^T = A (AT)T=A
求导公式如下:
∂ X T ∂ X = I \frac{\partial X^T}{\partial X} = I ∂X∂XT=I 求解出来是单位矩阵∂ X T A ∂ X = A \frac{\partial X^TA}{\partial X} = A ∂X∂XTA=A∂ A X T ∂ X = A \frac{\partial AX^T}{\partial X} = A ∂X∂AXT=A∂ A X ∂ X = A T \frac{\partial AX}{\partial X} = A^T ∂X∂AX=AT∂ X A ∂ X = A T \frac{\partial XA}{\partial X} = A^T ∂X∂XA=AT∂ X T A X ∂ X = ( A + A T ) X ; \frac{\partial X^TAX}{\partial X} = (A + A^T)X; ∂X∂XTAX=(A+AT)X; A不是对称矩阵∂ X T A X ∂ X = 2 A X ; \frac{\partial X^TAX}{\partial X} = 2AX; ∂X∂XTAX=2AX; A是对称矩阵
2.4 推导正规方程
θ
\theta
θ 的解
- 矩阵乘法公式展开
J ( θ ) = 1 2 ( X θ − y ) T ( X θ − y ) J(\theta) = \frac{1}{2}(X\theta - y)^T(X\theta - y) J(θ)=21(Xθ−y)T(Xθ−y)J ( θ ) = 1 2 ( θ T X T − y T ) ( X θ − y ) J(\theta) = \frac{1}{2}(\theta^TX^T - y^T)(X\theta - y) J(θ)=21(θTXT−yT)(Xθ−y)J ( θ ) = 1 2 ( θ T X T X θ − θ T X T y − y T X θ + y T y ) J(\theta) = \frac{1}{2}(\theta^TX^TX\theta - \theta^TX^Ty -y^TX\theta + y^Ty) J(θ)=21(θTXTXθ−θTXTy−yTXθ+yTy)
- 进行求导(注意X、y是已知量, θ \theta θ 是未知数):
J ′ ( θ ) = 1 2 ( θ T X T X θ − θ T X T y − y T X θ + y T y ) ′ J'(\theta) = \frac{1}{2}(\theta^TX^TX\theta - \theta^TX^Ty -y^TX\theta + y^Ty)' J′(θ)=21(θTXTXθ−θTXTy−yTXθ+yTy)′
- 根据上面求导公式进行运算:
J ′ ( θ ) = 1 2 ( X T X θ + ( θ T X T X ) T − X T y − ( y T X ) T ) J'(\theta) = \frac{1}{2}(X^TX\theta + (\theta^TX^TX)^T-X^Ty - (y^TX)^T) J′(θ)=21(XTXθ+(θTXTX)T−XTy−(yTX)T)J ′ ( θ ) = 1 2 ( X T X θ + X T X θ − X T y − X T y ) J'(\theta) = \frac{1}{2}(X^TX\theta + X^TX\theta -X^Ty - X^Ty) J′(θ)=21(XTXθ+XTXθ−XTy−XTy)J ′ ( θ ) = 1 2 ( 2 X T X θ − 2 X T y ) J'(\theta) = \frac{1}{2}(2X^TX\theta -2X^Ty) J′(θ)=21(2XTXθ−2XTy)J ′ ( θ ) = X T X θ − X T y J'(\theta) =X^TX\theta -X^Ty J′(θ)=XTXθ−XTyJ ′ ( θ ) = X T ( X θ − y ) J'(\theta) =X^T(X\theta -y) J′(θ)=XT(Xθ−y) 矩阵运算分配律
- 令导数 J ′ ( θ ) = 0 : J'(\theta) = 0: J′(θ)=0:
0 = X T X θ − X T y 0 =X^TX\theta -X^Ty 0=XTXθ−XTyX T X θ = X T y X^TX\theta = X^Ty XTXθ=XTy
- 矩阵没有除法,使用逆矩阵进行转化:
( X T X ) − 1 X T X θ = ( X T X ) − 1 X T y (X^TX)^{-1}X^TX\theta = (X^TX)^{-1}X^Ty (XTX)−1XTXθ=(XTX)−1XTyI θ = ( X T X ) − 1 X T y I\theta = (X^TX)^{-1}X^Ty Iθ=(XTX)−1XTyθ = ( X T X ) − 1 X T y \theta = (X^TX)^{-1}X^Ty θ=(XTX)−1XTy
到此为止,公式推导出来了~

2.5 凸函数判定
🚩判定损失函数是凸函数的好处在于我们可能很肯定的知道我们求得的极值即最优解,一定是全局最优解。
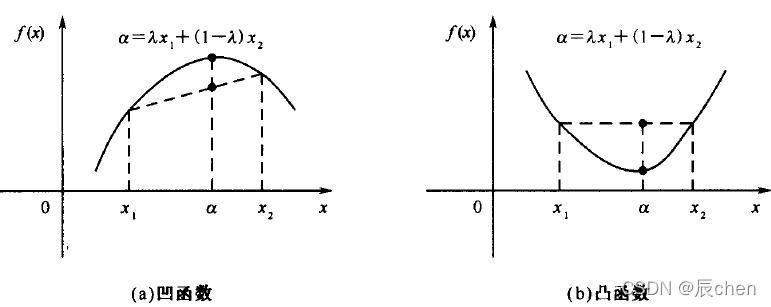
如果是非凸函数,那就不一定可以获取全局最优解,如下图: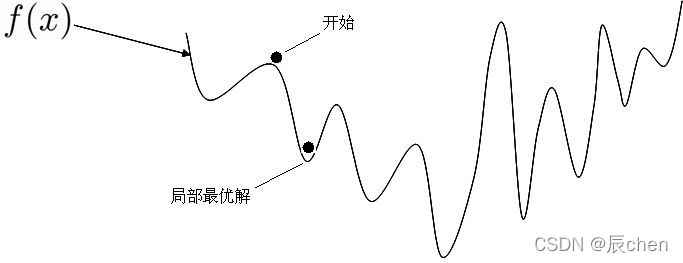
来一个更加立体的效果图: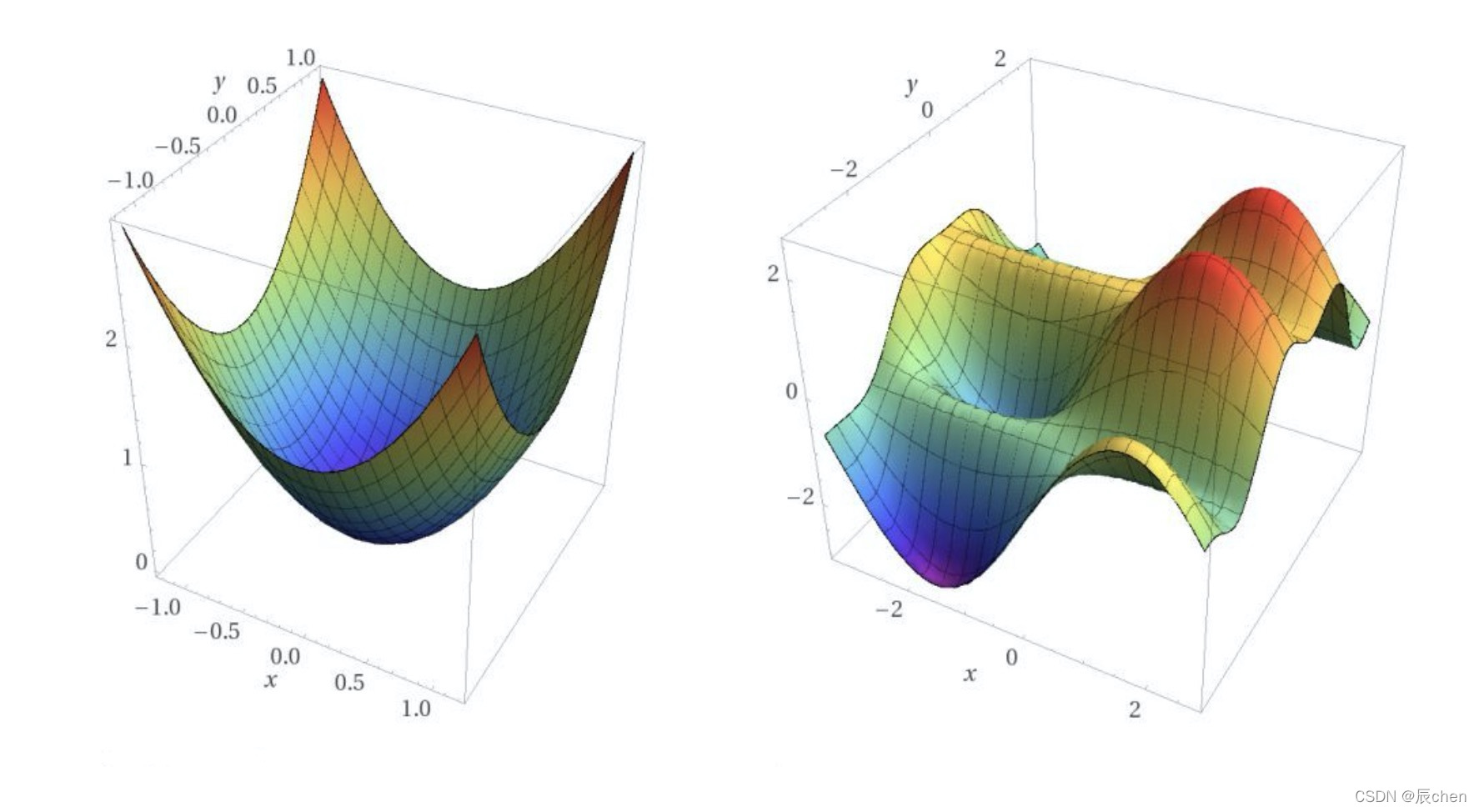
判定凸函数的方式: 判定凸函数的方式非常多,其中一个方法是看 黑塞矩阵 是否是 半正定 的。
黑塞矩阵
(
h
e
s
s
i
a
n
(hessian
(hessian
m
a
t
r
i
x
)
matrix)
matrix)是由目标函数在点
X
X
X 处的二阶偏导数组成的对称矩阵。
对于我们的式子来说就是在导函数的基础上再次对
θ
\theta
θ 来求偏导,结果就是
X
T
X
X^TX
XTX。所谓正定就是
X
T
X
X^TX
XTX 的特征值全为正数,半正定就是
X
T
X
X^TX
XTX 的特征值大于等于
0
0
0, 就是半正定。
J
′
(
θ
)
=
X
T
X
θ
−
X
T
y
J'(\theta) =X^TX\theta -X^Ty
J′(θ)=XTXθ−XTy
J
′
′
(
θ
)
=
X
T
X
J''(\theta) =X^TX
J′′(θ)=XTX
这里我们对
J
(
θ
)
J(\theta)
J(θ) 损失函数求二阶导数的黑塞矩阵是
X
T
X
X^TX
XTX ,得到的一定是半正定的,自己和自己做点乘嘛!
这里不用数学推导证明这一点。在机器学习中往往损失函数都是凸函数,到深度学习中损失函数往往是非凸函数,即找到的解未必是全局最优,只要模型堪用就好!机器学习特点是:不强调模型
100
%
100\%
100% 正确,只要是有价值的,堪用的,就
O
k
a
y
!
Okay!
Okay!
版权归原作者 辰chen 所有, 如有侵权,请联系我们删除。