人工智能与机器学习课程大作业（三、模糊逻辑）

本文为人工智能与机器学习课程大作业第三部分（三、模糊逻辑）

本文仅作学习参考使用！

其他章节跳转：

一、知识工程基础

二、函数逼近

三、模糊逻辑

四、函数优化

目　录

三、模糊逻辑

3.1 问题一分析与求解

   设论域U={x1,x2,x3,x4,x5}，A和B为论域U上的两个模糊集合，已知：

$A=\frac{0.2}{x_{1}}+\frac{0.3}{x_{2}}+\frac{0.5}{x_{3}}+\frac{0.6}{x_{4}}+\frac{1}{x_{5}}, B=\frac{0.1}{x_{1}}+\frac{0.4}{x_{3}}+\frac{1}{x_{4}}+\frac{0.7}{x_{5}}$

计算：

$A^{c},B^{c},A\cup B,A\cap B,A\cup A^{c},A\cap A^{c},A\cup B^{c},A\cap B^{c}$

求解：

$A^{c}=\frac{0.8}{x_{1}}+\frac{0.7}{x_{2}}+\frac{0.5}{x_{3}}+\frac{0.4}{x_{4}}+\frac{0}{x_{5}}$

$B^{c}=\frac{0.9}{x_{1}}+\frac{1}{x_{2}}+\frac{0.6}{x_{3}}+\frac{0}{x_{4}}+\frac{0.3}{x_{5}}$

$A\cup B=\frac{0.2}{x_{1}}+\frac{0.3}{x_{2}}+\frac{0.5}{x_{3}}+\frac{1}{x_{4}}+\frac{1}{x_{5}}$

$A\cap B=\frac{0.1}{x_{1}}+\frac{0}{x_{2}}+\frac{0.4}{x_{3}}+\frac{0.6}{x_{4}}+\frac{0.7}{x_{5}}$

$A\cup A^{c}=\frac{0.8}{x_{1}}+\frac{0.7}{x_{2}}+\frac{0.5}{x_{3}}+\frac{0.6}{x_{4}}+\frac{1}{x_{5}}$

$A\cap A^{c}=\frac{0.2}{x_{1}}+\frac{0.3}{x_{2}}+\frac{0.5}{x_{3}}+\frac{0.4}{x_{4}}+\frac{0}{x_{5}}$

$A\cup B^{c}=\frac{0.9}{x_{1}}+\frac{1}{x_{2}}+\frac{0.6}{x_{3}}+\frac{0.6}{x_{4}}+\frac{1}{x_{5}}$

$A\cap B^{c}=\frac{0.2}{x_{1}}+\frac{0.3}{x_{2}}+\frac{0.5}{x_{3}}+\frac{0}{x_{4}}+\frac{0.3}{x_{5}}$

3.2 问题二分析与求解

   设有论域X={x1,x2,x3}、Y={y1,y2,y3}、Z={z1,z2}上的模糊集合A、B、C且A=[0.5 0.7 0.1]、B=[0.2 0.1 0.8]、C=[0.6 1]、确定由模糊条件语句“If A and B then C”决定的模糊关系R，并确定当输入A1=[0.1 0.4 1]、B1=[1 0.3 0.1]时的输出C1。

求解：由于

$A\times B\rightarrow C$

$R_{1}=A^{T}\times B=\begin{bmatrix} 0.5\\ 0.7 \\ 0.1 \end{bmatrix}\times \begin{bmatrix} 0.2 & 0.1 & 0.8 \end{bmatrix}=\begin{bmatrix} 0.2 & 0.1 & 0.5\\ 0.2 & 0.1 & 0.7\\ 0.1 & 0.1 & 0.1 \end{bmatrix}$

把R1写成列向量的形式：

$R_{1}^{T}=\begin{bmatrix} 0.2 & 0.1 & 0.5 & 0.2 & 0.1 & 0.7 & 0.1 & 0.1 & 0.1 \end{bmatrix}^{T}$

则有：

$R=R_{1}^{T}\times C=\begin{bmatrix} 0.2 & 0.2\\ 0.1 & 0.1\\ 0.5 & 0.5\\ 0.2 & 0.2\\ 0.1 & 0.1\\ 0.6 & 0.7\\ 0.1 & 0.1\\ 0.1 & 0.1\\ 0.1 & 0.1 \end{bmatrix}$

由已知A1、B1，则：

$R_{2}=A_{1}^{T}\times B_{1}=\begin{bmatrix} 0.1\\ 0.4\\ 1 \end{bmatrix}\times \begin{bmatrix} 1 & 0.3 & 0.1 \end{bmatrix}=\begin{bmatrix} 0.1 & 0.1 & 0.1\\ 0.4 & 0.3 & 0.1\\ 1 & 0.3 & 0.1 \end{bmatrix}$

同理，将R2表示为列向量的形式：

$R_{2}^{T}=\begin{bmatrix} 0.1 & 0.1 & 0.1 & 0.4 & 0.3 & 0.1 & 1 & 0.3 & 0.1 \end{bmatrix}^{T}$

则：

$C_{1}=(A_{1}\times B_{1})o(A\times B\rightarrow C)=R_{2}^{T}oR=\begin{bmatrix} 0.2 & 0.2 \end{bmatrix}$

则最终得：

$C_{1}=\frac{0.2}{z_{1}}+\frac{0.2}{z_{2}}$

3.3 问题三分析与求解

   假设一个双输入/单输出系统，输入X∈[-5, 5] 和Y∈[-10, 10] 模糊化成三级：负、零、正，输出Z∈[-5, 5] 模糊化成五级：负大、负小、零、正小、正大。模糊规则表如下所示。适当选择隶属度函数后，设计一个基于Mamdani模型的模糊推理系统，绘制出输入/输出曲线，并计算当X和Y分别为1和-5以及-2和7时输出Z的大小，并分析选择不同隶属度函数对性能有何影响。

表3-1　X、Y、Z的模糊关系

X/Y=Z

负

零

正

负

正大

正小

零

正小

零

负小

正

零

负小

负大

3.3.1 实验步骤

   通过使用MATLAB/FUZZY工具箱实现，并建立模型，设计一个MISO双输入/单输出的系统，选定描述控制器的输入、输出变量的语义词汇，写入所给模糊规则表。在MATLAB中打开FUZZY工具箱，点击Edit，新增一个输入变量，并对输入输出变量命名，输入变量命名为为X、Y，输出变量为Z。更改输入输出范围和类型，输入变量为X、Y，范围分别设置为[-5, 5]、[-10, 10]，设置隶属度函数为trimf，设置X如图3-1所示，设置Y如图3-2所示。

图3-1　设置输入变量X

图3-2　设置输入变量Y

   输出变量Z的范围设置为[-5, 5]，隶属度函数设置为trimf，其中模糊规则选择mamdani，设置变量Z如图3-3所示。点击模糊规则推理机，编写如图3-4所示的对应输出输出关系，模糊规则，确定X、Y、Z的模糊关系如表3-1所示。

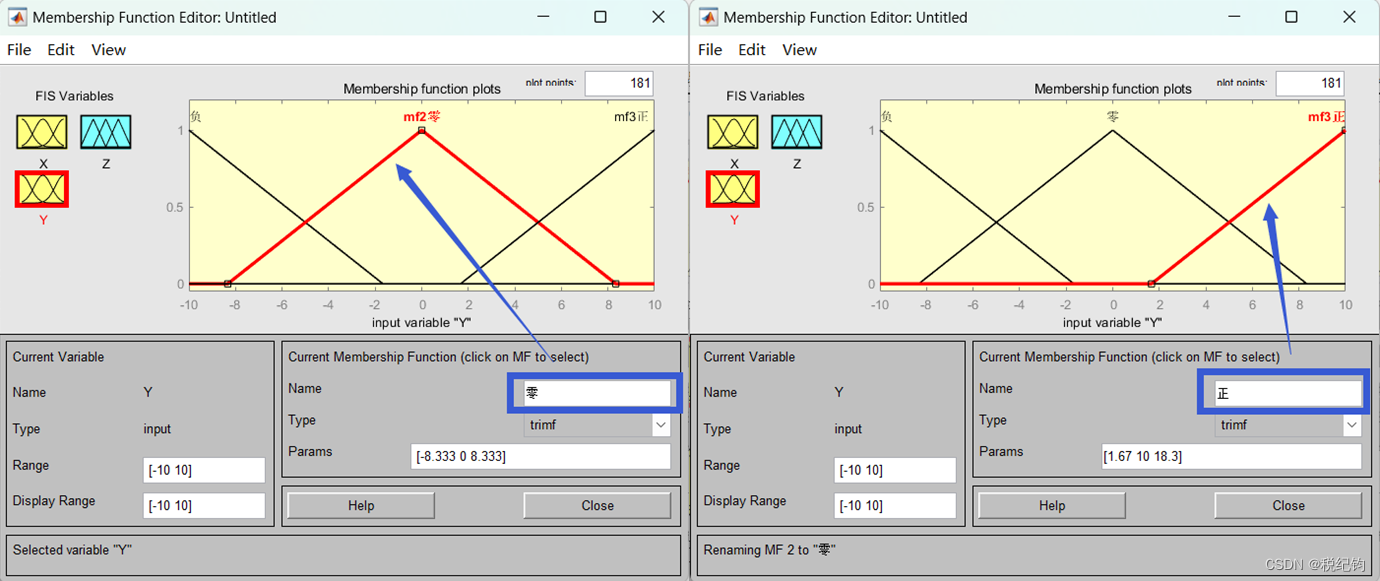
图3-3　设置输出变量Z

图3-4　X、Y、Z模糊关系设置

(a) 特性曲面 (b) 模糊规则浏览

图3-5　特性曲面与模糊规则浏览

   点击编辑器窗口中的“View-Surface”菜单，可得到如图3-5(a)所示的输入输出特性曲面。再点击编辑器窗口中“View-Rules”菜单命令，可以得到如图3-5(b)模糊规则浏览器，在其窗口左下角的iuput中分别输入1和-5以及-2和7，可得到图3-6，对应的输出结果分别为：Z=1.06和Z=-0.913。

(a) 输入[1, -5] (b) 输入[-2, 7]

图3-6　隶属度函数trimf对应输入输出结果

   采用隶属度函数trapmf，即更改对应的输入输出变量X、Y、Z的Type类型，均选择trapmf，如图3-7、图3-8(a)所示。点击编辑器窗口中的“View-Surface”菜单，可得到如图3-8(b)所示的输入输出特性曲面，再点击编辑器窗口中“View-Rules”菜单命令，在其窗口左下角的iuput中分别输入1和-5以及-2和7，可得到图3-9，对应的输出结果分别为：Z=1.24和Z=-1.35。

(a) 输入变量X (b) 输入变量Y

图3-7　修改输入隶属度函数为trapmf

(a) 输出变量Z (b) 输入输出特性曲面

图3-8　输出变量Z隶属度函数与输入输出特性曲面

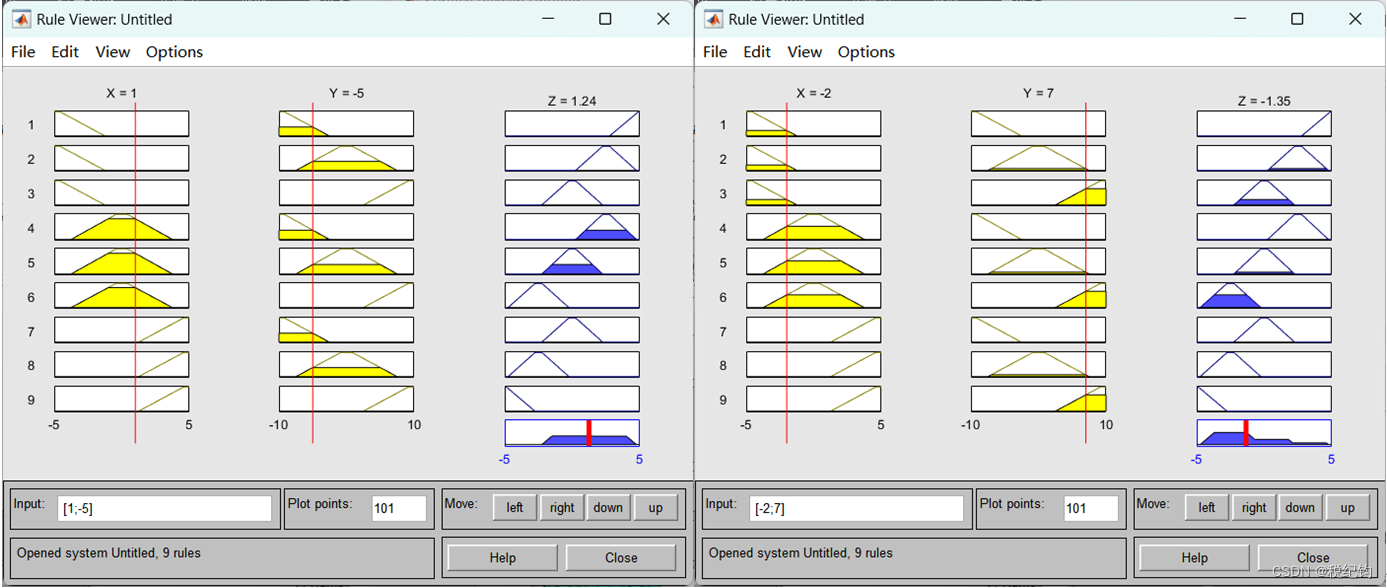
(a) 输入[1, -5] (b) 输入[-2, 7]

图3-9　隶属度函数trapmf对应输入输出结果

    采用隶属度函数gbellmf，得到如下图所示的输入输出特性曲面。

图3-10　隶属度函数gbellmf输入输出特性曲面

    输入[1;-5]和[-2;7]对应的输出结果分别为：Z=1.09，Z=-1.72，如图3-11所示。

(a) 输入[1, -5] (b) 输入[-2, 7]

图3-11　隶属度函数trapmf对应输入输出结果

   修改隶属度函数为gaussmf，输入输出特性曲面如图3-12所示。

图3-12　隶属度函数gaussmf输入输出特性曲面

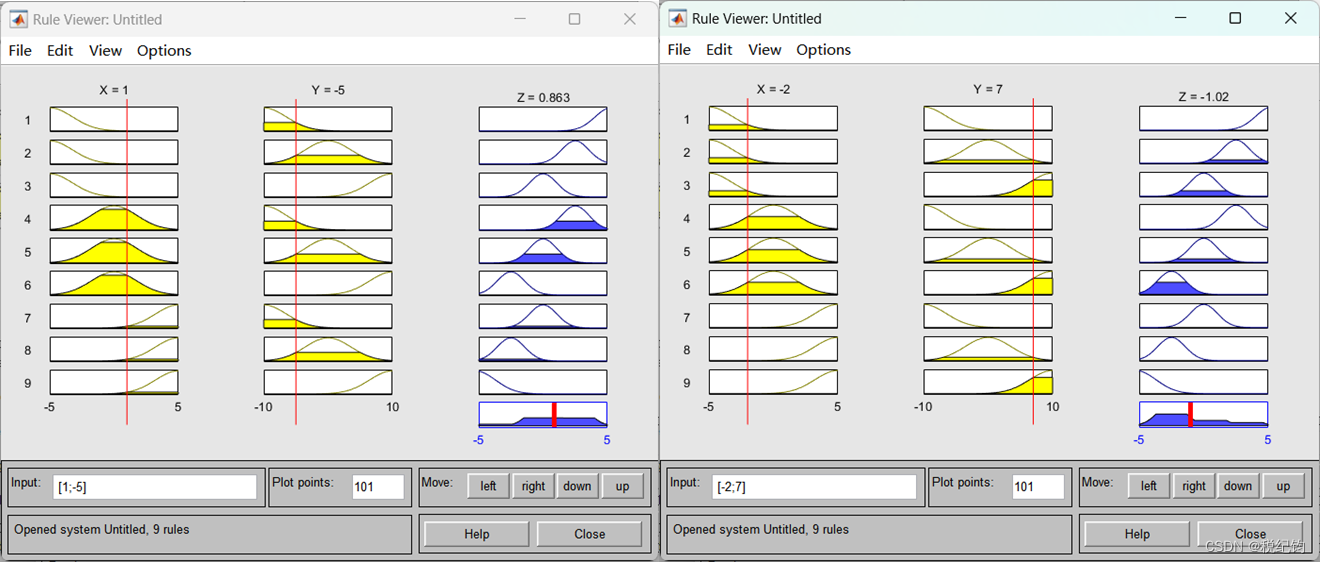
(a) 输入[1, -5] (b) 输入[-2, 7]

图3-13　隶属度函数trapmf对应输入输出结果

   如图3-13，输入[1;-5]和[-2;7]对应的输出结果分别为：Z=0.863，Z=-1.02。

3.3.2 实验总结

   隶属度函数依次设置为trimf、trapmf、gbellmf、gaussmf，输入X、Y分别输入[1, -5]、[-2, 7]，输出为Z，结果整理如表3-2所示。可以看到采用不同隶属函数，模糊推理的结果不同，隶属度函数曲线越尖锐，空值灵敏度越高，分辨率越高。

表3-2　不同隶属度函数输入输出结果

隶属度函数

trimf

-5

1.06

-2

-0.913

trapmf

-5

1.24

-2

-1.35

gbellmf

-5

1.09

-2

-1.72

gaussmf

-5

0.863

-2

-1.02

人工智能与机器学习课程大作业其他章节内容：一、知识工程基础；二、函数逼近；四、函数优化

标签：人工智能学习 matlab

本文转载自: https://blog.csdn.net/HISJJ/article/details/130439917
版权归原作者 税纪钧 所有，如有侵权，请联系我们删除。

人工智能与机器学习课程大作业（三、模糊逻辑）

目　录

三、模糊逻辑

发表评论