
朴素贝叶斯
一、概述
贝叶斯分类算法是统计学的一种概率分类方法,朴素贝叶斯分类是贝叶斯分类中最简单的一种。其分类原理就是利用贝叶斯公式根据某特征的先验概率计算出其后验概率,然后选择具有最大后验概率的类作为该特征所属的类。之
所以称之为”朴素”,是因为贝叶斯分类只做最原始、最简单的假设:所有的特征之间是统计独立的。
假设某样本X有
a
1
{a}_{1}
a1,
a
2
{a}_{2}
a2,
a
3
{a}_{3}
a3…
a
n
{a}_{n}
an个属性,那么有P(X) = P(
a
1
{a}_{1}
a1,
a
2
{a}_{2}
a2…
a
n
{a}_{n}
an) =P(
a
1
{a}_{1}
a1)*P(
a
2
{a}_{2}
a2)*…*P(
a
n
{a}_{n}
an)满足样的公式就说明特征统计独立。
1.条件概率公式
条件概率(Condittional probability),就是指在事件B发生的情况下,事件A发生的概率,用P(A|B)来表示。
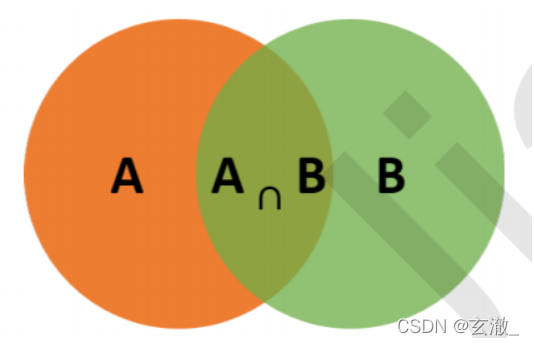
根据文氏图可知:在B事件发生的情况下,事件A发生的概率就是P(A∩B)除以P(B)
P
(
A
∣
B
)
=
P
(
A
∩
B
)
P
(
B
)
P(A|B)\, =\, \frac {P(A\cap B)} {P(B)}
P(A∣B)=P(B)P(A∩B) ⇒
P
(
A
∣
B
)
P
(
B
)
=
P
(
A
∩
B
)
P(A|B)\, P(B)=\, P(A\cap B)
P(A∣B)P(B)=P(A∩B)
同理可得:
P
(
B
∣
A
)
P
(
A
)
=
P
(
A
∩
B
)
P(B|A)\, P(A)=\, P(A\cap B)
P(B∣A)P(A)=P(A∩B)
所以:
P
(
B
∣
A
)
P
(
A
)
=
P
(
A
∣
B
)
P
(
B
)
P(B|A)\, P(A)=\, P(A|B)P(B)
P(B∣A)P(A)=P(A∣B)P(B) ⇒
P
(
A
∣
B
)
=
P
(
B
∣
A
)
P
(
A
)
P
(
B
)
P(A|B)=\frac {P(B|A)P(A)} {P(B)}
P(A∣B)=P(B)P(B∣A)P(A)
接着看全概率公式,如果事件
A
1
{A}_{1}
A1,
A
2
{A}_{2}
A2,…
A
n
{A}_{n}
An 构成一个完备事件且都有正概率,那么对于任意一个事件B则有:
P
(
B
)
=
P
(
B
A
1
)
+
P
(
B
A
2
)
+
.
.
.
+
P
(
B
A
n
)
P(B)\, =\, P(B{A}_{1})+P(B{A}_{2})+...+P(B{A}_{n})
P(B)=P(BA1)+P(BA2)+...+P(BAn)
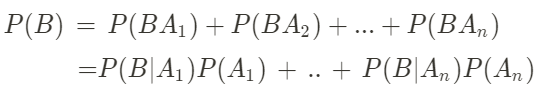
P
(
B
)
=
∑
i
=
1
n
P
(
A
i
)
P
(
B
∣
A
i
)
P(B)\, =\, \sum ^{n}_{i=1} {P({{A}_{i}}_{})P(B|{A}_{i})}
P(B)=∑i=1nP(Ai)P(B∣Ai)
贝叶斯判断
根据条件概率和全概率公式,可以得到贝叶斯公式如下:
P
(
A
∣
B
)
=
P
(
A
)
P
(
B
∣
A
)
P
(
B
)
P(A|B)=P(A)\frac {P(B|A)} {P(B)}
P(A∣B)=P(A)P(B)P(B∣A)
P
(
A
i
∣
B
)
=
P
(
A
i
)
P
(
B
∣
A
)
∑
i
=
1
n
P
(
A
i
)
P
(
B
∣
A
i
)
P({A}_{i}|B)=P({A}_{i})\frac {P(B|A)} {\sum ^{n}_{i=1} {P({A}_{i})P(B|{A}_{i})}}
P(Ai∣B)=P(Ai)∑i=1nP(Ai)P(B∣Ai)P(B∣A)
**
P(A)称为"先验概率"(Prior probability)
**,即在B事件发生之前,我们对A事件概率的一个判断。
**
P(A|B)称为"后验概率"(Posterior probability)
**,即在B事件发生之后,我们对A事件概率的重新评估。
**
P(B|A)/P(B)称为"可能性函数"(Likely hood)
**,这是一个调整因子,使得预估概率更接近真实概率。
所以条件概率可以理解为:**
后验概率 = 先验概率 * 调整因子
**
如果"可能性函数">1,意味着"先验概率"被增强,事件A的发生的可能性变大;
如果"可能性函数"=1,意味着B事件无助于判断事件A的可能性;
如果"可能性函数"<1,意味着"先验概率"被削弱,事件A的可能性变小。
朴素贝叶斯种类
在scikit-learn中,一共有3个朴素贝叶斯的分类算法。
分别是GaussianNB,MultinomialNB和BernoulliNB。
1. GaussianNB
GaussianNB就是先验为**
高斯分布(正态分布)的朴素贝叶斯
**,假设每个标签的数据都服从简单的正态分布。

其中 为Y的第k类类别。 和 为需要从训练集估计的值。
这里,用scikit-learn简单实现一下GaussianNB。
#导入包import pandas as pd
from sklearn.naive_bayes import GaussianNB
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
#导入数据集from sklearn import datasets
iris=datasets.load_iris()
#切分数据集
Xtrain, Xtest, ytrain, ytest = train_test_split(iris.data,
iris.target,
random_state=12)#建模
clf = GaussianNB()
clf.fit(Xtrain, ytrain)#在测试集上执行预测,proba导出的是每个样本属于某类的概率
clf.predict(Xtest)
clf.predict_proba(Xtest)#测试准确率
accuracy_score(ytest, clf.predict(Xtest))
MultinomialNB
MultinomialNB就是先验为多项式分布的朴素贝叶斯。它假设特征是由一个简单多项式分布生成的。多项分布可以
描述各种类型样本出现次数的概率,因此多项式朴素贝叶斯非常适合用于描述出现次数或者出现次数比例的特征。
该模型常用于文本分类,特征表示的是次数,例如某个词语的出现次数。
多项式分布公式如下:
P
(
X
j
=
x
j
∣
Y
=
C
k
)
=
x
j
l
+
ξ
m
k
+
n
ξ
P({X}_{j}={x}_{j}|Y={C}_{k})=\frac {{x}_{jl\, }+ξ} {{m}_{k}+nξ}
P(Xj=xj∣Y=Ck)=mk+nξxjl+ξ
其中,
P
(
X
j
=
x
j
∣
Y
=
C
k
)
P({X}_{j}={x}_{j}|Y={C}_{k})
P(Xj=xj∣Y=Ck)是第k个类别的第j维特征的第l个取值条件概率。
m
k
{m}_{k}
mk是训练集中输出为第k类的样本个
数。 ξ为一个大于0的常数,常常取为1,即拉普拉斯平滑。也可以取其他值。
BernoulliNB
BernoulliNB就是先验为伯努利分布的朴素贝叶斯。假设特征的先验概率为二元伯努利分布,即如下式: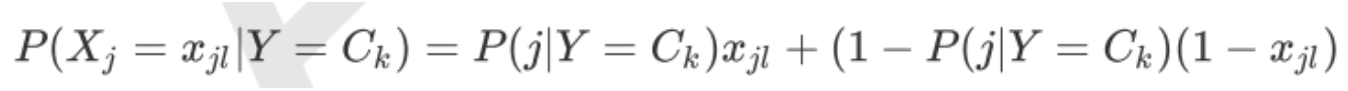
此时 只有两种取值。
x
j
l
{x}_{jl}
xjl 只能取值0或者1。
在伯努利模型中,每个特征的取值是布尔型的,即true和false,或者1和0。
在文本分类中,就是一个特征有没有在一个文档中出现。
总结
- 一般来说,如果样本特征的分布大部分是连续值,使用GaussianNB会比较好。
- 如果如果样本特征的分布大部分是多元离散值,使用MultinomialNB比较合适。
- 如果样本特征是二元离散值或者很稀疏的多元离散值,应该使用BernoulliNB。
版权归原作者 玄澈_ 所有, 如有侵权,请联系我们删除。