作者丨科技猛兽
编辑丨极市平台
本文首发于极市平台公众号,转载请获得授权并标明出处。
本文目录
1 脉冲神经网络简介
2 脉冲神经网络原理
3 脉冲神经网络数据集
4 脉冲神经网络训练方法
5 脉冲神经网络评价指标
1 脉冲神经网络简介
脉冲神经网络 (SNN) 属于第三代神经网络模型,实现了更高级的生物神经模拟水平。除了神经元和突触状态之外,SNN 还将时间概念纳入了其操作之中,是一种模拟大脑神经元动力学的一类很有前途的模型。
那么什么是第一代和第二代神经网络模型呢?
第一代神经网络
第一代神经网络又称为感知器,在1950年左右被提出来,它的算法只有两层,输入层输出层,主要是线性结构。它不能解决线性不可分的问题,对稍微复杂一些的函数都无能为力,如异或操作。
第二代神经网络:BP 神经网络
为了解决第一代神经网络的缺陷,在1980年左右 Rumelhart、Williams 等人提出第二代神经网络多层感知器 (MLP)。和第一代神经网络相比,第二代在输入层之间有多个隐含层的感知机,可以引入一些非线性的结构,解决了之前无法模拟异或逻辑的缺陷。
第二代神经网络让科学家们发现神经网络的层数直接决定了它对现实的表达能力,但是随着层数的增加,优化函数愈发容易出现局部最优解的现象,由于存在梯度消失的问题,深层网络往往难以训练,效果还不如浅层网络。
所有对目前机器学习有所了解的人都听说过这样一个事实:目前的人工神经网络是第二代神经网络。它们通常是全连接的,接收连续的值,输出连续的值。尽管当代神经网络已经让我们在很多领域中实现了突破,但它们在生物学上是不精确的,其实并不能模仿生物大脑神经元的运作机制。
第三代神经网络:脉冲神经网络
第三代神经网络,脉冲神经网络 (Spiking Neural Network,SNN) ,旨在弥合神经科学和机器学习之间的差距,使用最拟合生物神经元机制的模型来进行计算,更接近生物神经元机制。脉冲神经网络与目前流行的神经网络和机器学习方法有着根本上的不同。SNN 使用脉冲——这是一种发生在时间点上的离散事件——而非常见的连续值。每个峰值由代表生物过程的微分方程表示出来,其中最重要的是神经元的膜电位。本质上,一旦神经元达到了某一电位,脉冲就会出现,随后达到电位的神经元会被重置。对此,最常见的模型是 Leaky Integrate-And-Fire (LIF) 模型。此外,SNN 通常是稀疏连接的,并会利用特殊的网络拓扑。
然而,关于 SNN 作为人工智能和神经形态计算机群体中的计算工具的实用价值,长期以来一直存在争论。尤其是和人工神经网络 (ANN) 相比。在过去的几年里,这些怀疑减缓了神经形态计算 (neuromorphic computing ) 的发展,而随着深度学习的快速进步,研究人员试图从根本上缓解这个问题,人们想要通过加强 SNN 的手段,如改善训练算法,来缓解这个问题。
与成熟有效的人工神经网络 (ANN) 训练算法:误差反向传播算法 (Back Propagation) 不同,神经网络研究中最困难的问题之一是由于复杂的动力学和脉冲的不可微性质导致的训练困难。
为了提升脉冲神经网络的精度,已有一些前人的工作做出了探索,如:
- Spike timing dependent plasticity (STDP) :无监督学习方法
1 Unsupervised learning of digit recognition using spike-timing-dependent plasticity
- 添加奖励机制
2 Combining stdp and reward-modulated stdp in deep convolutional spiking neural networks for digit recognition
- 把预训练好的 ANN 转化为 SNN
3 Spiking deep convolutional neural networks for energy-efficient object recognition
4 Spiking deep residual network
5 Fast-classifying, high-accuracy spiking deep networks through weight and threshold balancing
6 Training spiking deep networks for neuromorphic hardware
7 Conversion of continuous-valued deep networks to efficient event-driven networks for image classification
为了提升 ANN 与 SNN 的兼容性,通常把 bias 去掉,使用 ReLU 激活函数,把 max-pool 换成 average-pool 等。把 ANN 转化成 SNN 时,通常包括 weight/activation normalization,threshold tuning, sampling error compensation 等操作以维持精度。
- 脉冲神经网络使用 BP 算法训练
8 Hybrid macro/micro level backpropagation for training deep spiking neural networks
9 Training deep spiking neural networks using backpropagation
10 Spatio-temporal backpropagation for training high-performance spiking neural networks
11 Direct training for spiking neural networks: Faster, larger, better
在执行反向传播时,梯度可以沿着空间维度通过聚合脉冲传播,也可以沿着时间和空间2个维度通过计算膜电势的梯度传播。
简而言之,通过上述努力,SNN 在视觉识别任务中的应用精度逐渐接近 ANN。
由于 SNN 缺乏专门的benchmark,许多工作直接使用 ANN 的 benchmark 来验证 SNN 模型。例如,用于 ANN 验证的图像数据集被简单地转换为 Spike 版本,用于 SNN 训练和测试。 此外,网络的准确性仍然是主要的评估指标,但众所周知,我们的大脑在绝对识别准确性方面,通常比现有的人工智能机器表现得差。这反映了我们需要更全面和公平的衡量标准来评估和模拟生物大脑工作方式的 SNN。简而言之,由于不适当的评估指标,目前的 SNN 无法击败 ANN。因此,出现了1个开放的问题,即:
如何评估 SNN 是有意义的?
Training spiking deep networks for neuromorphic hardware
这篇文章将预训练好的 ANN 转化成 SNN,在这个工作里面作者考虑到了 SNN 网络的 Efficiency,而不仅仅是 Accuracy。评价一个 SNN 时要从多个角度考量,比如:application accuracy,memory cost, compute cost 。
在以 ANN 主导的评价指标和任务中,相同大小的 SNN 无法打败 ANN。但是在以 SNN 主导的评价指标和任务中,SNN 的表现会更好。
2 脉冲神经网络原理
如下图1所示是ANN 和 SNN 的单个基本神经元。
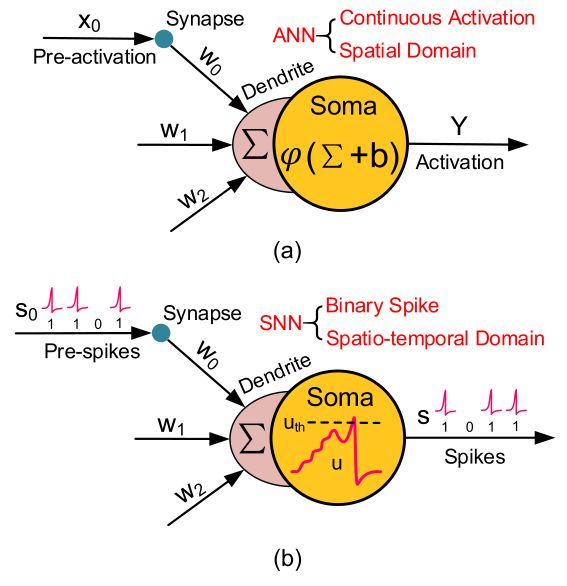
(a) 图是典型的单个 ANN 神经元,ANN 的计算方法是:
y
=
ϕ
(
b
+
∑
j
x
j
w
j
)
(1)
y=\phi (b+\sum_j x_jw_j)\tag{1}
y=ϕ(b+j∑xjwj)(1)
式中,
ϕ
(
⋅
)
\phi(\cdot)
ϕ(⋅) 是非线性的激活函数。
X
0
X_0
X0 代表上个神经元过来的连续的激活值 (Pre-activation),通过突触 (Synapse) 传递到树突的位置 (Dendrite),并且最终由细胞体 (Soma) 来处理这个激活值 (具体处理方法就是1式)。
ANN 中的神经元使用高精度和连续值编码的激活值进行相互通信,并且只在空间域 (spatial domain,即 layer by layer) 传播信息。从上述方程可以看出,输入和权重的相乘和累加 (MAC) 是网络的主要操作。
(b) 图是典型的单个 SNN 神经元,它的结构与 ANN 神经元相似,但行为不同。脉冲神经元之间的交流通过 binary 的 events,而不是连续的激活值。
S
0
S_0
S0 代表上个神经元过来的一个一个的脉冲 (Spike),通过突触 (Synapse) 传递到树突的位置 (Dendrite),并且最终由细胞体 (Soma) 来处理这些脉冲 (具体处理方法就是2式)。
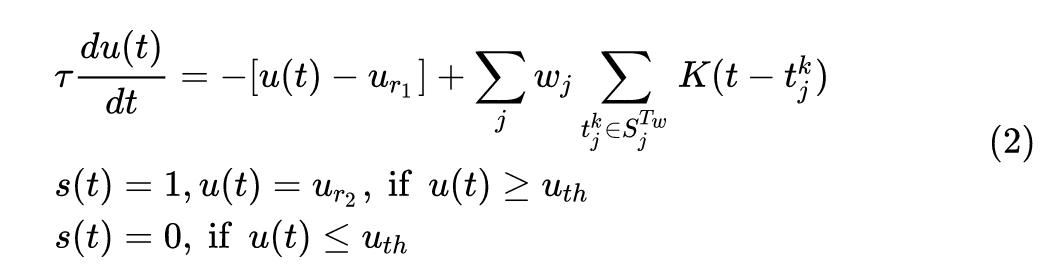
这个式子看起来很麻烦,我们先来理解下每个变量的含义。
式中
t
t
t 代表时间步长,
τ
\tau
τ 是常数,
u
u
u 和
s
s
s 代表膜电位和输出峰值。
u
r
1
u_{r_1}
ur1 和
u
r
2
u_{r_2}
ur2 分别是静息电位和重置电位。
w
j
w_j
wj 是第
j
j
j 个输入突触的权重。
t
j
k
t_j^k
tjk 是当第
j
j
j 个输入突触的第
k
k
k 个脉冲在
T
w
T_w
Tw 这个积分时间窗口内激发了 (即状态为1) 的时刻。
K
(
⋅
)
K(\cdot)
K(⋅) 是代表延时效应的核函数。
T
w
T_w
Tw 是积分时间窗口。
u
t
h
u_{th}
uth 是个阈值,代表要不要点火 (Fire) 一次。
接下来我们用人话解释一下2式是什么意思:
1 当膜电位
u ( t ) u(t) u(t) (也就是细胞体 Soma 这个隐含电位) 高于阈值 u t h u_{th} uth 时,脉冲神经元看做一次点火,此时输出电位 s ( t ) s(t) s(t) 置为1,同时膜电位 u ( t ) u(t) u(t) 回归到重置电位 u r 2 u_{r_2} ur2 。2 当膜电位
u ( t ) u(t) u(t) (也就是细胞体 Soma 这个隐含电位) 低于阈值 u t h u_{th} uth 时,不点火,此时输出电位 s ( t ) s(t) s(t) 保持为0。3 在每个 time step,膜电位
u ( t ) u(t) u(t) 的更新过程满足一个微分方程,即2.1式。4 在每个 time step,膜电位
u ( t ) u(t) u(t) 值应下降 u ( t ) − u r 1 u(t)-u_{r_1} u(t)−ur1 这么大的值,其中 u r 1 u_{r_1} ur1 是静息电位。5 同时在每个 time step,膜电位
u ( t ) u(t) u(t) 值应上升一个值,这个值来的大小与这个神经元的 j j j 个输入突触有关,每个输入突触的权值是 w j w_j wj ,这个突触对膜电位上升的贡献值是 ∑ t j k ∈ S j T w K ( t − t j k ) \sum_{t_j^k\in S_j^{T_w}}K(t-t_j^k) ∑tjk∈SjTwK(t−tjk) ,即在 S j T w S_j^{T_w} SjTw 个脉冲中,如果 t j k t_j^k tjk 时刻的输入脉冲是点火状态 (即1状态),那么计算一次 K ( t − t j k ) K(t-t_j^k) K(t−tjk) 并累积起来。
与 ANN 不同的是,SNN 使用脉冲的序列来传递信息,每个脉冲神经元都经历着丰富的动态行为。 具体而言,除了空间域中的信息传播外,时间域中的过去历史也会对当前状态产生紧密的影响。 因此,与主要通过空间传播和连续激活的神经网络相比,神经网络通常具有更多的时间通用性,但精度较低。 由于只有当膜电位超过一个阈值时才会激发尖峰信号,因此整个尖峰信号通常很稀疏。 此外,由于尖峰值 (Spike) 是二进制的,即0或1,如果积分时间窗口
T
w
T_w
Tw 调整为1,输入和权重之间的乘法运算就可以消除。由于上述原因,**与计算量较大的 ANN 网络相比,SNN 网络通常可以获得较低的功耗。**
3 脉冲神经网络数据集
这一节介绍下脉冲神经网络的基本数据集。
像 MNIST,CIFAR10 这类基于帧的静态图像,广泛应用于 ANN 中,我们称之为 ANN-oriented dataset,如下图2的前2行所示。
CIFAR-10:32×32×3 RGB image,Training set:50000,Testing set:10000
MNIST:28×28×1 grayscale image,Training set:60000,Testing set:10000

图2的后2行 N-MNIST 和 DVS-CIFAR10 叫做 SNN-oriented dataset。这里的 DVS 叫做 dynamic vision sensor,代表使用了动态视觉传感器扫描每张 images 得到的 spike 数据。它除了具有与 ANN-oriented dataset 相似的空间信息外,还包含更多的动态时间信息,而且尖峰事件与神经网络中的信号格式自然兼容,因此我们称之为 SNN-oriented dataset。
DVS 产生两个通道的脉冲事件,命名为 On 和Off 事件 (分别如图2中红色和蓝色所示)。因此,DVS 将每个图像转换为
r
o
w
×
c
o
l
u
m
n
×
2
×
T
row\times column\times 2\times T
row×column×2×T 的脉冲模式。
N-MNIST:34×34×2×T spatio-temporal spike pattern,Training set:60000,Testing set:10000
DVS-CIFAR-10:128×128×2×T spatio-temporal spike pattern,Training set:9000,Testing set:1000
一般来说,ANN 接收帧为基础的图像,而 SNN 接收事件驱动的脉冲信号。因此,有时需要将相同的数据转换为另一个域中的不同形式来处理。本文以视觉识别任务为例,主要介绍了四种信号转换方法,如下图3所示。
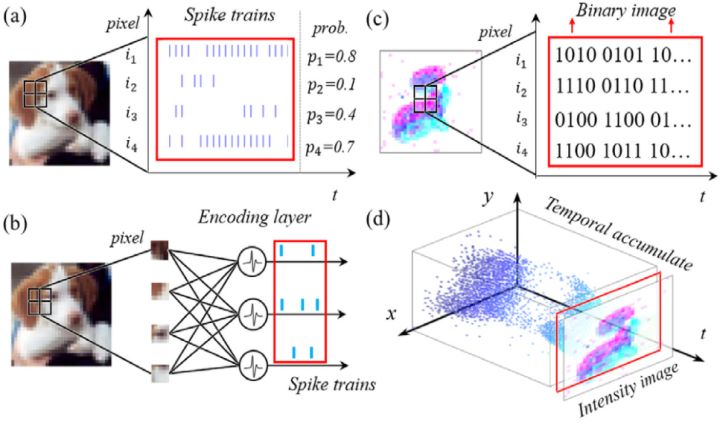
Image to spike pattern
由图片信号转化为脉冲信号的方法比较直观。
一种方法是:如图3 (a) 所示。 在每一个时间步骤,采样的原始像素强度 (pixel intensity) 到一个二进制值 (通常归一化为[0,1]),其中的这个强度值就等于发射一个脉冲的概率。这个采样样遵循一个特定的概率分布,例如伯努利分布或泊松分布。
例如,图3(a) 中的
i
1
i_1
i1 神经元,对应于标准化强度为 0.8 的 intensity,产生一个二进制尖峰序列,跟随着伯努利分布
B
(
0.8
,
T
)
B(0.8,T)
B(0.8,T) 。这里
T
T
T 是取样的时间窗口。
再例如,图3(a) 中的
i
2
i_2
i2 神经元,对应于标准化强度为 0.1 的 intensity,产生一个二进制尖峰序列,跟随着伯努利分布
B
(
0.1
,
T
)
B(0.1,T)
B(0.1,T) 。这里
T
T
T 是取样的时间窗口。
这种方法在取样的时间窗口
T
T
T 比较短时有一个较大的精度损失。
另一种方法是: 如图3 (b) 所示。使用一个编码器来产生全局的脉冲信号。这个编码器的每个神经元接受图片多个像素的强度值intensity 信号作为输入, 而产生脉冲作为输出。 虽然编码层是 ANN-SNN 混合层,而不是像网络中的其他层那样的完整 SNN 层,但它的权重是可训练的,因为我们的训练方法也是 BP 兼容的。由于神经元的数量可以灵活定制,参数也可以调整,因此它可以适应整体最佳化问题,从而获得更高的精确度。
Spike pattern to image
由脉冲信号转化为图片信号的输出主要有2种:
- binary image with 0/1 pixels。
- intensity image with real-valued pixels。
如图3(c) 所示,代表把脉冲pattern转化为二值图片。2D 脉冲 pattern 可以直接看做一个二值图像 (每个脉冲 Event 代表像素强度为1,否则像素强度为0)。 为了转换为强度图像 (Intensity image),需要在一个时间窗
T
T
T 内随时间对脉冲时间的累积。
如图3(d)所示,代表把脉冲pattern转化为强度图片。描述了100毫秒内脉冲事件的累积过程,累积脉冲数将被归一化为具有适当强度值的像素。由于 DVS 的相对运动和固有噪声,使得图像常常模糊,边缘特征模糊。这种转换只允许一个强大的假设,每个脉冲位置不应该移动,否则将严重损害生成的图像质量。
- ANN-oriented workloads
ANN-oriented workloads 的含义是目标是识别在 ANN 中经常使用的基于帧的数据集 (如 MNIST 和 CIFAR10)。有3种基准模型:
1 如下图4(a) 所示,最直接的解决办法是 ANN 训练 + ANN 推理。
2 如下图4(b) 所示,这种方案是先在 ANN 数据集上使用 BP 算法训练一个 ANN,再把这个训练好的 ANN 转化成 SNN。这个 SNN 与 ANN 拥有相同的结构,但是不同的神经元。这个 SNN 在推理时使用的是 ANN 数据集转化得到的 SNN-oriented dataset。
3 如下图4(c) 所示,这种方案是直接使用 SNN-oriented dataset 训练一个 SNN,训练方法是 BP-inspired Training。在每个时刻和位置的梯度直接由 spatio-temporal backpropagation (STBP) 方法得到。

- SNN-oriented workloads
SNN-oriented workloads 的含义是目标是识别在 SNN 中经常使用的脉冲数据集 (如 N-MNIST 和 DVS-CIFAR10)。有2种基准模型:
1 如下图5(a) 所示,把脉冲数据集转化成图片,即 ANN-oriented dataset,然后使用 BP 算法训练 ANN 并推理。脉冲数据集转化成图片的方法就是图3的 (c)(d) 所示。
2 如下图5(b) 所示,这种方案是直接使用 SNN-oriented dataset 训练一个 SNN,训练方法是 BP-inspired Training。在每个时刻和位置的梯度直接由 spatio-temporal backpropagation (STBP) 方法得到。
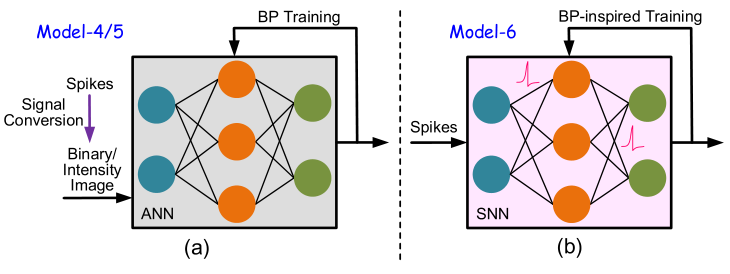
4 脉冲神经网络训练方法
- ANN 的 BP 训练方法
可以用下式表示:
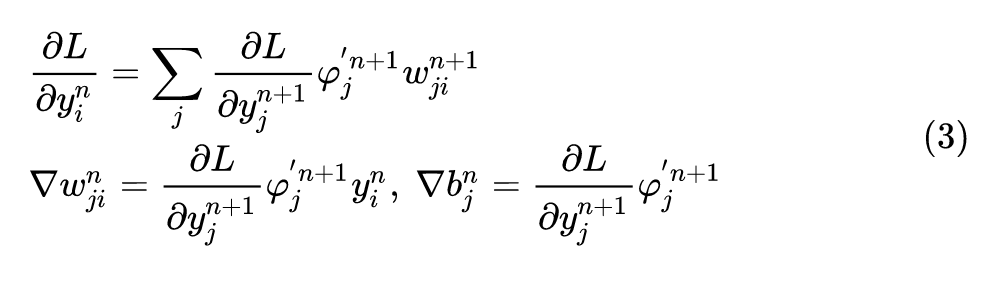
式中,
φ
j
′
n
+
1
\varphi_j^{'n+1}
φj′n+1 是
n
+
1
n+1
n+1 层的第
j
j
j 个神经元的激活函数的导数。
L
L
L 是损失函数,比如可以是 MSE Loss:
L
=
1
2
∣
∣
Y
−
Y
label
∣
∣
2
2
L=\frac{1}{2}||Y-Y_{\text{label}}||_2^2
L=21∣∣Y−Ylabel∣∣22 。
- SNN 的 STBP (时空反向传播) 训练方法
基于的前向模型是2式的 LIF 的 SNN 模型,为了阅读的方便再把2式写一遍。
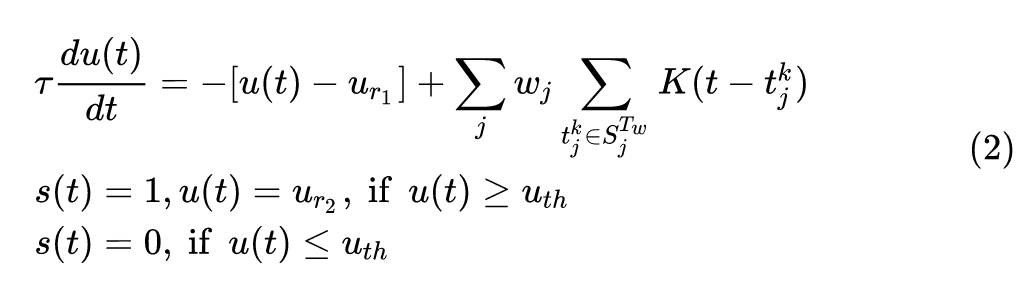
LIF 模型的迭代版本可以用下式表示:
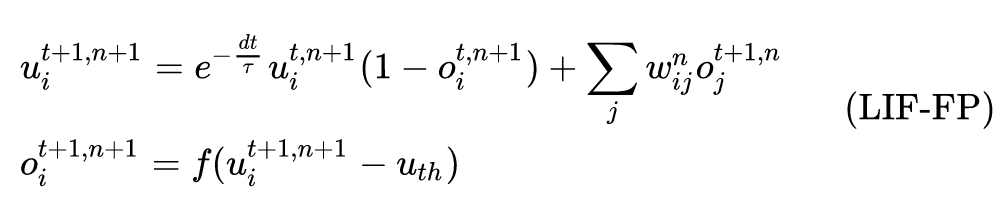
式中,
o
o
o 代表脉冲输出,
t
t
t 代表 time step,
n
n
n 代表 layer index。
e
−
d
t
τ
e^{-\frac{dt}{\tau}}
e−τdt 代表膜电位的延迟效应。
f
(
⋅
)
f(\cdot)
f(⋅) 是阶跃函数 (step function)。 这种迭代的 LIF 模型包含了原始神经元模型中的所有行为,包括集成 (integration),触发 (fire) 和重置 (reset)。
注意,为了简单起见,我们在原来的 LIF 模型中设置了
u
r
1
=
u
r
2
=
0
,
T
w
=
1
,
K
(
⋅
)
=
1
u_{r_1}=u_{r_2}=0,T_w=1,K(\cdot)=1
ur1=ur2=0,Tw=1,K(⋅)=1 。给定迭代 LIF 模型,梯度沿着时间和空间维度传播,**LIF 模型的迭代版本的参数更新可以按照如下方式进行:**

从膜电位
u
u
u 到输出
o
o
o 是个阶跃函数,它是不可导的。为了解决这个问题,有下面这个辅助函数计算输出
o
o
o 到膜电位
u
u
u 的导数值:
∂
o
∂
u
=
1
a
sign
(
∣
u
−
u
t
h
∣
<
a
2
)
(4)
\frac{\partial o}{\partial u}=\frac{1}{a}\text{sign}(|u-u_{th}|<\frac{a}{2})\tag{4}
∂u∂o=a1sign(∣u−uth∣<2a)(4)
式中,参数
a
a
a 决定了梯度宽度。
L
L
L 是损失函数,比如可以是 MSE Loss:
L
=
1
2
∣
∣
1
T
∑
t
=
1
T
O
t
,
N
−
Y
label
∣
∣
2
2
L=\frac{1}{2}||\frac{1}{T}\sum_{t=1}^{T}{O^{t,N}}-Y_{\text{label}}||_2^2
L=21∣∣T1∑t=1TOt,N−Ylabel∣∣22 。
5 脉冲神经网络评价指标
众所周知,基于 SNN 的模型通常无法在绝对识别准确性方面击败当前基于 ANN 的 AI 系统,而真正的大脑在其他指标上表现更好,比如操作效率。然而,在最近的研究中,识别精度仍然是判断哪个模型 (ANN 或 SNN) 更好的主流指标,特别是在算法研究中。这是不公平的,因为 ANN 和 SNN 有非常不同的特点。例如,数据的精度 ANN 比 SNN 更高,这就使得在网络大小相同的情况下,ANN 通常比 SNN 更容易获得更好的识别精度。所有这些都表明模型评估需要更全面的度量。除了通常的精度比较,这里我们进一步介绍了内存和计算成本作为互补的评估指标。
- 识别精度 (Recognition accuracy)
在 ANN 中,这个精确度意味着正确识别样本的百分比。如果标签类别与模型预测的最大激活值相同,则识别结果对当前样本是正确的。
在 SNN 中,我们首先计算每一个输出神经元的 fire rate,即脉冲率,当然是在给定的时间窗
T
T
T 内。然后取 fire rate 最高的那个神经元作为输出,写成公式就是:
C
^
=
arg
max
i
{
1
T
∑
t
=
1
T
o
i
t
,
N
}
(5)
\hat C=\arg\max_i \left\{ \frac{1}{T}\sum_{t=1}^{T}{o_i^{t,N}} \right\}\tag{5}
C^=argimax{T1t=1∑Toit,N}(5)
式中,
o
i
t
,
N
o_i^{t,N}
oit,N 代表网络的第
N
N
N 层,第
i
i
i 个神经元在第
t
t
t 时刻的输出。
下面介绍的内存花销和计算花销都是指推理过程。原因有2点,一方面, spatio-temporal gradient propagation 相对于推理过程来讲非常复杂。另一方面, 大多数支持 SNN 的神经形态学设备只执行推理阶段 (inference phase)。
- 内存花销 (Memory cost)
通常,在嵌入式设备上部署模型时,内存占用 (Memory cost) 非常重要。
在 ANN 中,存储器成本包括 权重内存 (weight memory) 和激活值内存 (activation memory)。activation memory 的开销被忽略,但是如果使用查找表来实现的话应该被计算在内。
在 SNN 中,内存成本包括 权重内存 (weight memory),膜电位内存 (membrane potential memory) 和脉冲内存 (spike memory)。其他参数如点火阈值
u
t
h
u_{th}
uth 和时间常数
τ
\tau
τ 等可以忽略,因为它们可以被同一层或整个神经网络的所有神经元共享。只有当脉冲触发时,脉冲内存 (spike memory) 开销才会出现。总之,内存开销可以通过下式计算:
A
N
N
:
M
=
M
w
+
M
a
S
N
N
:
M
=
M
w
+
M
p
+
M
s
(6)
\begin{aligned} &A N N: M=M_{w}+M_{a} \\ &S N N: M=M_{w}+M_{p}+M_{s} \end{aligned} \tag{6}
ANN:M=Mw+MaSNN:M=Mw+Mp+Ms(6)
式中,
M
w
,
M
a
,
M
p
M_w,M_a,M_p
Mw,Ma,Mp 由网络结构决定,而
M
s
M_s
Ms 由每个时间戳最大脉冲数动态地决定。
- 计算花销 (Compute cost)
计算开销对于运行延迟和能量消耗是至关重要的。
在 ANN 中,计算开销主要由方程中的 MAC 运算决定。
在 SNN 中,主要的计算成本来自脉冲输入的这个积分的过程。与 ANN 有两点不同:
- 代价高昂的乘法运算可以省去,如果假设 T w = 1 , K ( ⋅ ) = 1 T_w=1,K(\cdot)=1 Tw=1,K(⋅)=1 。此时树突的这个积分运算 (integration,注意看2式) 就变成了 ∑ j w j s j = ∑ j ′ w j ′ \sum_jw_js_j=\sum_{j^{'}}w_j^{'} ∑jwjsj=∑j′wj′ ,成为了一个纯加法运算。
- 积分是事件驱动的,这意味着如果没有收到脉冲信号就不会进行计算。
计算开销可以通过下式计算:
A
N
N
:
C
=
C
m
u
l
+
C
a
d
d
S
N
N
:
C
=
C
a
d
d
(7)
\begin{aligned} &A N N: C=C_{m u l}+C_{a d d} \\ &S N N: C=C_{a d d} \end{aligned} \tag{7}
ANN:C=Cmul+CaddSNN:C=Cadd(7)
在细胞体中的计算开销 (例如 ANN 中的激活函数和 SNN 中的膜电位更新和触发活动) 被忽略,这是神经网络设备中的一种常见方式。
注意,在 SNN 中,
C
a
d
d
C_{add}
Cadd 与 Spike 事件的总数成正比。
版权归原作者 极市平台 所有, 如有侵权,请联系我们删除。