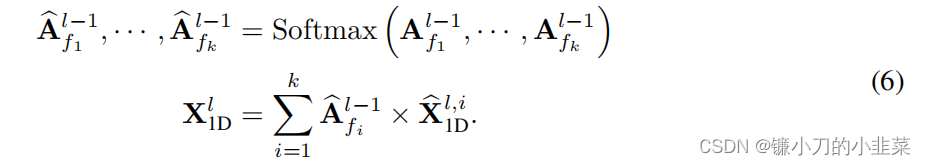论文解读 ——TimesNet 模型
论文一:TEMPORAL 2D-VARIATION MODELING
FOR GENERAL TIME SERIES ANALYSIS
论文:
文章解读
本文是2023年2月ICLR发表出来的一篇关于深度学习的预测模型,该模型围绕时序变化建模展开,设计提出了时序基础模型TimesNet,在长时、短时预测、缺失值填补、异常检测、分类五大任务上实现了全面领先。(这点就比较夸张了,看图)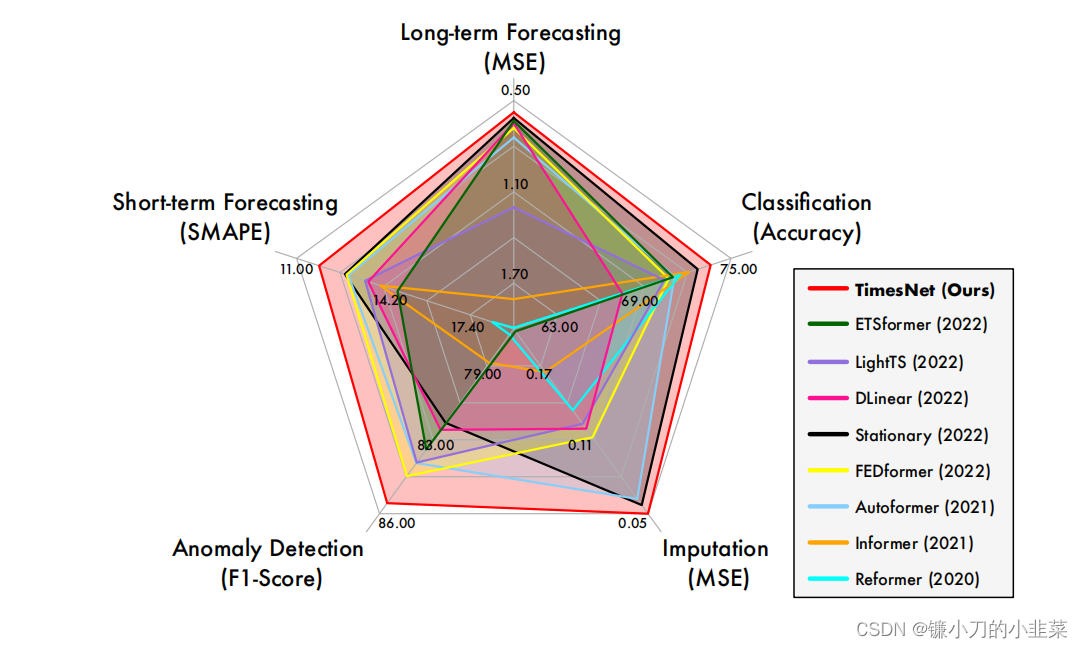
粉色部分代表TimesNet模型在5大领域均处于领先水平。
理论部分
先看图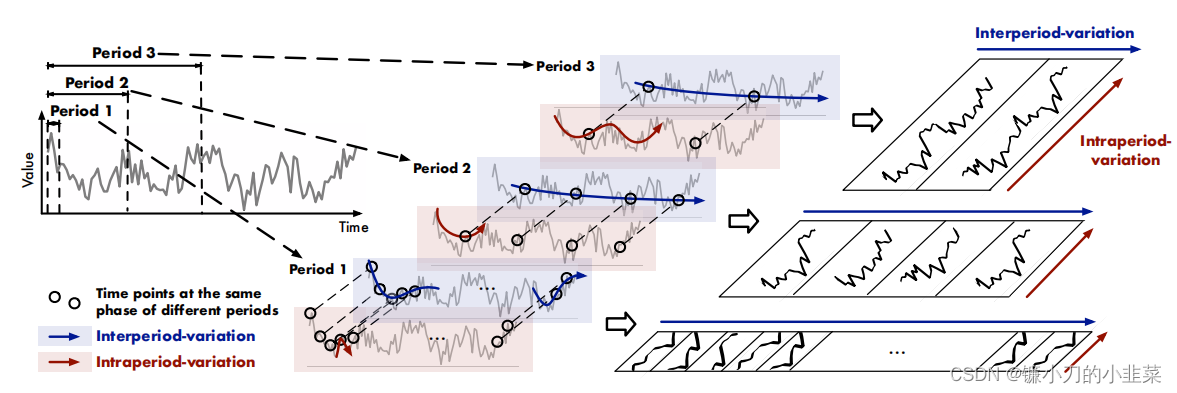
这张图表示 利用傅里叶变换(FFT)求时序序列周期,然后按照求得的不同周期进行分解(下面简单讲解一下)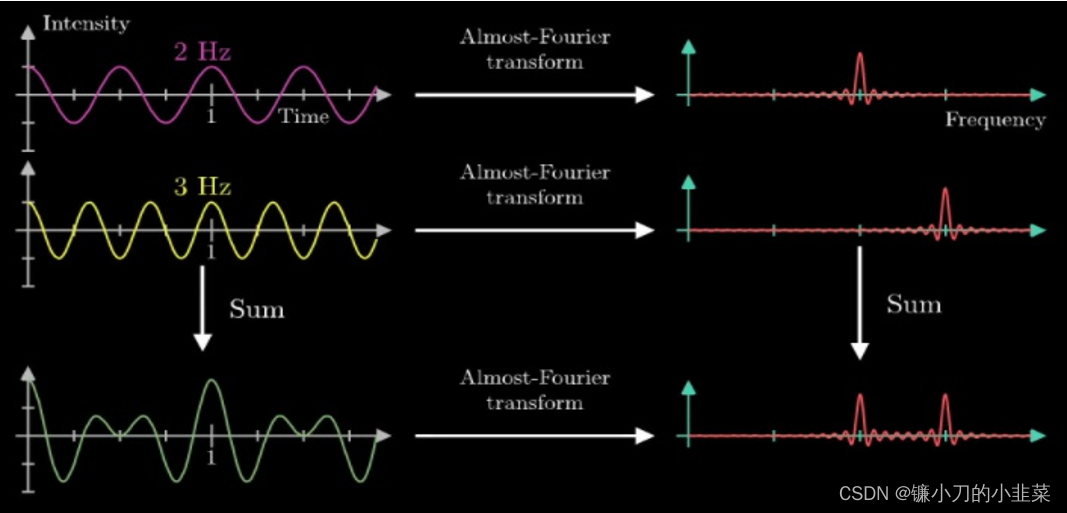
这张图中可以看出,一个线性序列可以转换成两个正弦函数,然后分别求这俩正弦函数的周期和幅度,一个2Hz,一个3Hz。
对于任意一个序列,利用FFT将其转换为多组三角函数的组合,然后求出所有三角函数的周期的最小共倍数。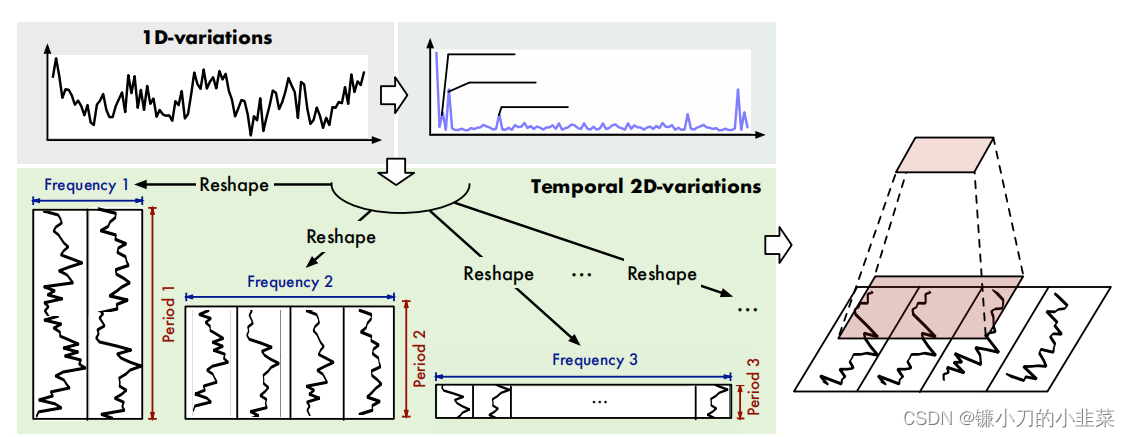
如上图所示,将其按照不同的频率进行切割,这样就将一维时序序列边成了多张二维张量。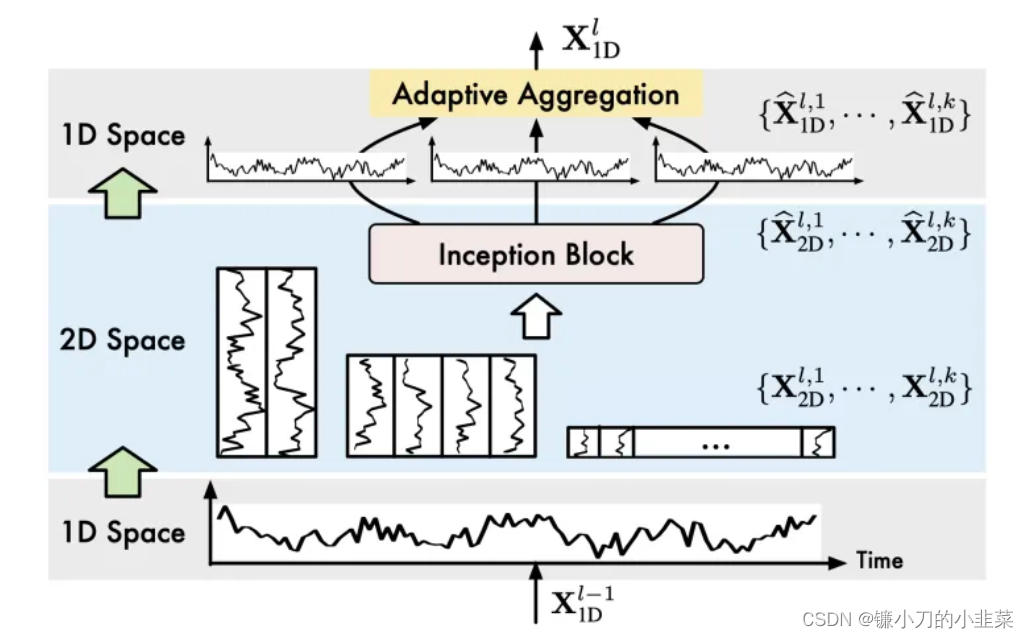
这里呢,有一个比较巧妙的设计,就是整个模型的运算过程中,其实是一维变成二维,再又二维又变成一维的过程,但是中间保留了周期内及周期间的特征。如下图为整体模型部分: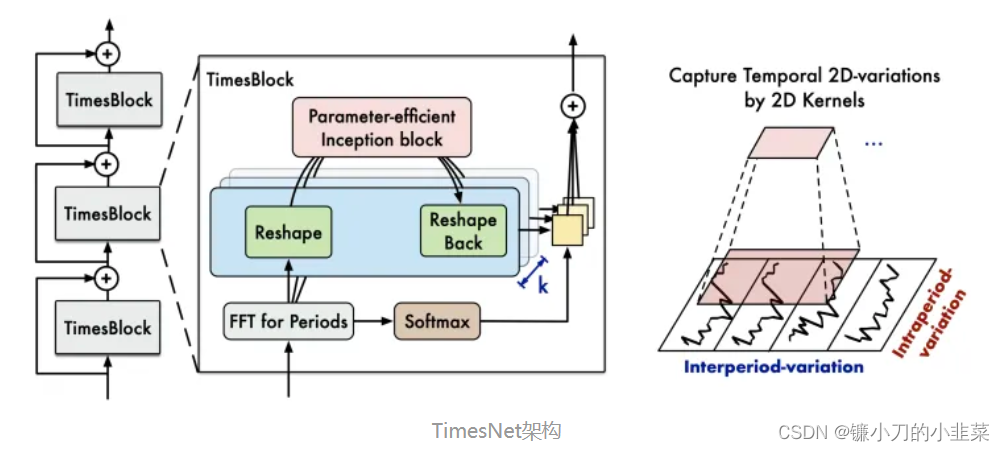
整个模型和nbeats 长得很像。该模型也是有一个一个的timesblock 模块构成。
公式推导
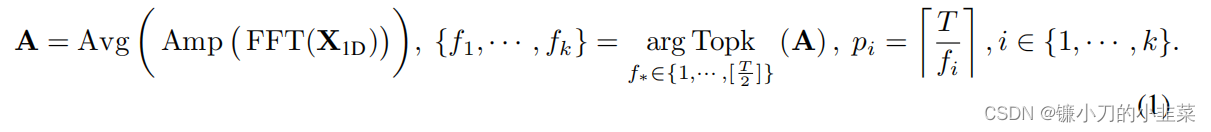
公式(1)FFT(.)代表求对应序列的频率f (f的取值范围由1到2/T), Amp (.) 表示求频率对应的周期幅度p,Avg(.)文中表示说是(which is averaged from C dimensions by Avg(·) )我理解的意思是说,首先对应C组(多组时序序列),每组时序序列都可用FFT求出一组对应的pi(周期幅度)出来。这里的平均值,不是说所有的相加求平均,而是求多组序列里面的共同周期幅度(均有的)(也包括最小公倍数的形式)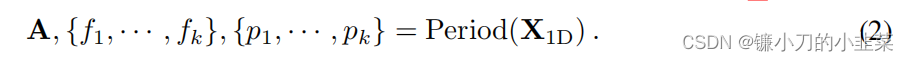
公式二表示确定的频率和对应的周期长度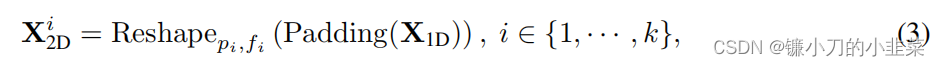
公式三中 pi fi 表示二维张量的行数和列数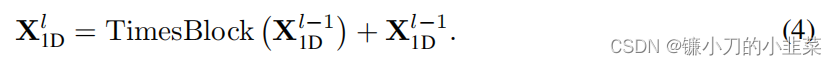
如上图所示,TimesNet由堆叠的TimesBlock组成。输入序列首先经过嵌入层得到深度特征。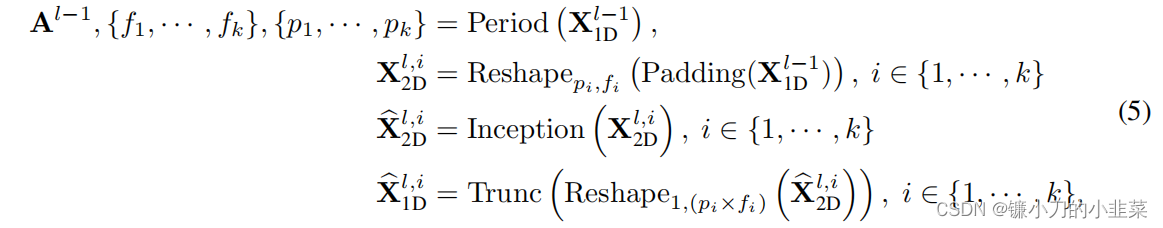
(1)一维变换至二维:首先对输入的一维时序特征提取周期,并将之转换成为二维张量来表示二维时序变化。
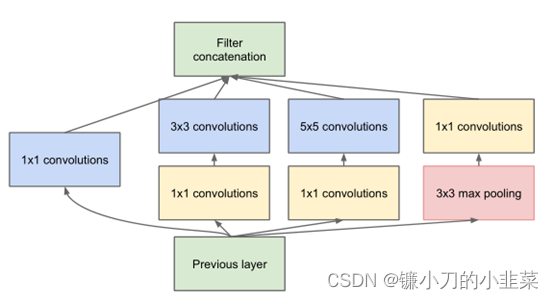
(2)提取二维时序变化表征:对于二维张量,由于其具有二维局部性,因此,我们可以使用2D卷积提取信息。在这里,我们选取了经典的Inception模型。
https://arxiv.org/pdf/1512.00567v3.pdf
inception v1网络
(3)二维变换至一维:对于提取的时序特征,我们将其转化回一维空间以便进行信息聚合。这里选择的是Adaptive aggregation,我们将得到的一维表征以其对应频率的强度进行加权求和,得到最终输出。
https://arxiv.org/pdf/2106.13008.pdf
实验部分
版权归原作者 镰小刀的小韭菜 所有, 如有侵权,请联系我们删除。