深度学习常用损失MSE、RMSE和MAE

MSE 均方差损失（ Mean Squared Error Loss）

MSE是深度学习任务中最常用的一种损失函数，也称为 L2 Loss

MSE是真实值与预测值的差值的平方然后求和平均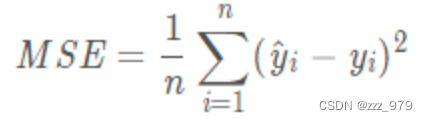

范围[0,+∞)，当预测值与真实值完全相同时为0，误差越大，该值越大

MSE 曲线的特点是光滑连续、可导，便于使用梯度下降算法，是比较常用的一种损失函数。而且，MSE 随着误差的减小，梯度也在减小，这有利于函数的收敛，即使固定学习因子，函数也能较快取得最小值。

平方误差有个特性，就是当 yi 与 f(xi) 的差值大于 1 时，会增大其误差；当 yi 与 f(xi) 的差值小于 1 时，会减小其误差。这是由平方的特性决定的。也就是说， MSE 会对误差较大（>1）的情况给予更大的惩罚，对误差较小（<1）的情况给予更小的惩罚。从训练的角度来看，模型会更加偏向于惩罚较大的点，赋予其更大的权重。

如果样本中存在离群点，MSE 会给离群点赋予更高的权重，但是却是以牺牲其他正常数据点的预测效果为代价，这最终会降低模型的整体性能。

RMSE 均方根误差（Root Mean Square Error）

RMSE就是对MSE开方之后的结果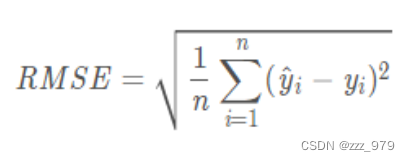

MAE 平均绝对误差损失 （Mean Absolute Error Loss）

MAE也是常用的损失函数之一，也称为 L1 Loss

MAE是真实值与预测值的差值的绝对值然后求和平均

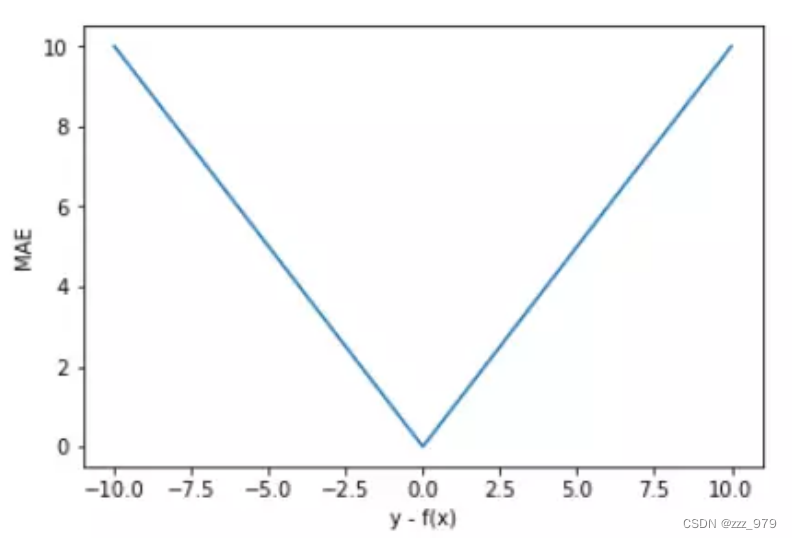
MAE 的曲线呈 V 字型，连续但在 y-f(x)=0 处不可导，计算机求解导数比较困难。而且 MAE 大部分情况下梯度都是相等的，这意味着即使对于小的损失值，其梯度也是大的。这不利于函数的收敛和模型的学习。

值得一提的是，MAE 相比 MSE 有个优点就是 MAE 对离群点不那么敏感，更有包容性。因为 MAE 计算的是误差 y-f(x) 的绝对值，无论是 y-f(x)>1 还是 y-f(x)<1，没有平方项的作用，惩罚力度都是一样的，所占权重一样。

MSE与MAE区别

1、一般情况下，MSE收敛速度更快

2、MAE不易受到异常值影响

3、误差关系

MAE损失与误差间为线性关系，而MSE与误差间则是平方关系，当误差越来越大，会使得MSE损失远远大于MAE损失，当MSE损失非常大时，对模型训练的影响也很大

4、鲁棒性

MSE假设服从标准高分布，而MAE服从拉普拉斯分布
而拉普拉斯分布本身就对异常值更具鲁棒性，当异常值出现时，拉普拉斯分布相比高斯分布受到的影响要小很多，因此以拉普拉斯分布假设的MAE在处理异常值是比高斯分布假设的MSE更加鲁棒

实现代码

基于上述原理，可以采用多种方式实现MSE和MAE

MSE

1、直接使用pytorch库实现

`torch.nn.MSELoss(reduction='mean')# reduction取值 - none / mean (返回loss和的平均值) / sum (返回loss的和) /默认为 mean`

2、直接根据数学公式计算

loss =1/(2*m)* np.sum((y-y_pred)**2)

MAE

1、直接使用pytorch库实现

torch.nn.L1Loss(reduction='mean')# reduction取值 - none / mean (返回loss和的平均值) / sum (返回loss的和) /默认为 mean

2、直接根据数学公式计算

loss =1/m * np.sum(np.abs(y-y_pred))