MultiHeadAttention多头注意力作为Transformer的核心组件,其主要由多组自注意力组合构成。
1. self-Attention自注意力机制
在NLP任务中,自注意力能够根据上下文词来重新构建目标词的表示,其之所以被称之为注意力,在于从上下文词中去筛选目标词更需要关注的部分,比如"他叫小明","他"这个词更应该关注"小明"这个上下文。
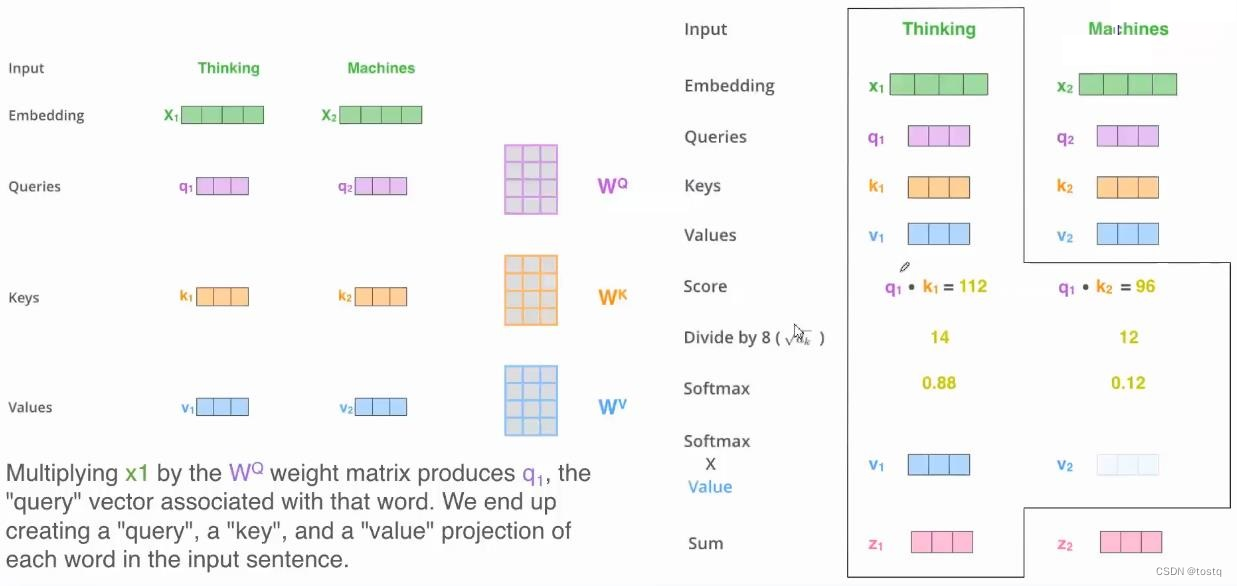
上图提示了一个输入为两个单词[Thinking, Matchines]的序列在经过自注意力构建后的变换过程:
通过Embeding层,两个单词的one-hot向量转换为embedding向量X=[x1, x2]
通过三组矩阵运算得到query、key、value值,这三组矩阵的输入都是原来同一个输入向量[x1,x2],这也是被称之为自注意力的原因。
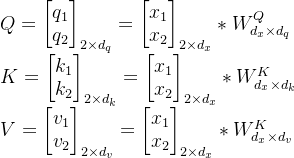计算query、key间的相似度得分,为了提升计算效率,此处采用缩放点积注意力,其需要query、key向量的维度是相等的,并且都满足零均值和单位方差,此时得分表示:
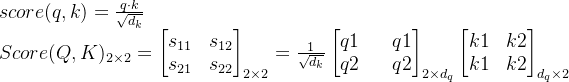对相似度得分矩阵求softmax进行归一化(按axis=1维进行),在实际中由于进行transformer中的输入序列要求是定长的,因此会有补余向量,此时这里softmax会有一个掩蔽操作,将补余部分都置为0。
![softmax(\begin{bmatrix} \xrightarrow[]{s_{11} \ s_{12}}\\ \xrightarrow[]{s_{21} \ s_{22}}\end{bmatrix})=\begin{bmatrix} p_{11} & p_{12}\\ p_{21} & p_{22} \end{bmatrix}](https://latex.csdn.net/eq?softmax%28%5Cbegin%7Bbmatrix%7D%20%5Cxrightarrow%5B%5D%7Bs_%7B11%7D%20%5C%20s_%7B12%7D%7D%5C%5C%20%5Cxrightarrow%5B%5D%7Bs_%7B21%7D%20%5C%20s_%7B22%7D%7D%5Cend%7Bbmatrix%7D%29%3D%5Cbegin%7Bbmatrix%7D%20p_%7B11%7D%20%26%20p_%7B12%7D%5C%5C%20p_%7B21%7D%20%26%20p_%7B22%7D%20%5Cend%7Bbmatrix%7D)乘以value向量得到输出z:
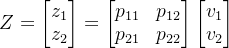
完成了结构的分析后,接下来,我们考虑一个新的问题,为什么自注意力机制会有效?通过三组矩阵Q、K、V我们获得了原来的输入三种不同表征形式,其通过query-key的比较来衡量目标词和上下文词的相似性关联,通过value来提取词的本质特征,最终通过自注意力机制,我们建立了结合上下文信息的词的新特征向量,其本质是特征提取器。
2. MultiHeadAttention多头注意力机制
多头注意力是多组自注意力构件的组合,上文已经提到自注意力机制能帮助建立包括上下文信息的词特征表达,多头注意力能帮忙学习到多种不同类型的上下文影响情况,比如"今天阳光不错,适合出去跑步",在不同情景下,"今天"同"阳光"、"跑步"的相关性是不同,特别是头越多,越有利于捕获更大更多范围的相关性特征,增加模型的表达能力。

上图描述了多头注意力的处理过程,其实际上将多个自注意机制的产出再经过参数矩阵得到一个新输出。我们将上述自注意步骤引入多头情况,介绍如何通过矩阵来计算,其由3组自注意力组合,输入为2个单词的序列。
query、key、value表征向量的计算
计算query、key间的相似度得分
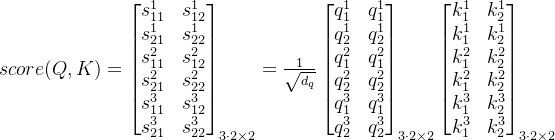对相似度得分矩阵求softmax
乘以value向量得到各自注意力模块输出,并乘以输出权重矩阵得到最终输出矩阵O,其最终还是得到了多头注意力的输出,其
为输出词向量维度,如果其维度等于输入词向量维度时,输出和输入的尺度是一致的,因此多头注意力机制本质仍是特征抽取器。
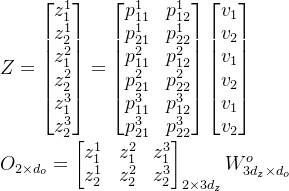
3. MultiHeadAttention多头注意力机制的代码

上图左侧为单点积注意力Dot-Product Attention组件的结构(当Q,K,V为同一输入时称之为自注意力),右侧为多个单注意力组件组成多头注意力,以下是paddle的实现代码:
class DotProductAttention(nn.Layer):
def __init__(self, query_size, query_vec_size, hidden_vec_size, **kwargs):
"""
input:
query_size: int, 序列长度(词数)
query_vec_size: int, 词向量长度
hidden_vec_size: int, 输出词向量长度
"""
super(DotProductAttention, self).__init__(**kwargs)
self.query_size = query_size
self.query_vec_size = query_vec_size
self.hidden_vec_size = hidden_vec_size
# 线性变换层
self.W_q = nn.Linear(query_vec_size, hidden_vec_size)
self.W_k = nn.Linear(query_vec_size, hidden_vec_size)
self.W_v = nn.Linear(query_vec_size, hidden_vec_size)
def forward(self, queries, keys, values, valid_lens):
"""
input:
queries,keys,values: tensor([batch_size, query_size, query_vec_size]), 输入
valid_lens: tensor([batch_size]), 序列中有效长度
output:
output: tensor([batch_size, query_size, hidden_vec_size]), 输出
"""
#1. Linear: queries, keys, values的线性变换, out shape: [batch_size, query_size, hidden_vec_size]
queries = self.W_q(queries)
keys = self.W_k(keys)
values = self.W_v(values)
# 2. score, shape: [batch_size, query_size, query_size]
scores = paddle.bmm(queries, keys.transpose((0, 2, 1))) / math.sqrt(self.hidden_vec_size)
scores = scores.reshape([-1, self.query_size])
# 3. mask, shape: [batch_size * query_size, query_size]
mask = paddle.arange(self.query_size, dtype=paddle.float32)[None, :] < paddle.repeat_interleave(valid_lens, self.query_size)[:, None]
scores[~mask] = float(-1e6)
# 4. softmax [batch_size, query_size, query_size]
scores = scores.reshape([-1, self.query_size, self.query_size])
scores = nn.functional.softmax(scores, axis=-1)
# 5. output [batch_size, query_size, query_size] * [batch_size, query_size, hidden_vec_size]
return paddle.bmm(scores, values)
在实际中,多个单注意力组件的计算可以通过同一矩阵进行并行计算,如第2节所描述,以下完成最终多头注意力的代码,可以看出其同单注意力的代码几乎差不多:
class MultiHeadAttention(nn.Layer):
def __init__(self, query_size, query_vec_size, hidden_vec_size, output_vec_size, head_num, **kwargs):
"""
input:
query_size: int, 序列长度(词数)
query_vec_size: int, 词向量长度
hidden_vec_size: int, 变换层词向量长度
output_vec_size: int, 输出层词向量长度
head_num: int, 头数
"""
super(MultiHeadAttention, self).__init__(**kwargs)
self.query_size = query_size
self.query_vec_size = query_vec_size
self.hidden_vec_size = hidden_vec_size
self.output_vec_size = output_vec_size
self.head_num = head_num
# 线性变换层
self.W_q = nn.Linear(query_vec_size, hidden_vec_size * head_num)
self.W_k = nn.Linear(query_vec_size, hidden_vec_size * head_num)
self.W_v = nn.Linear(query_vec_size, hidden_vec_size * head_num)
self.W_o = nn.Linear(hidden_vec_size * head_num, output_vec_size)
def forward(self, queries, keys, values, valid_lens):
"""
input:
queries,keys,values: tensor([batch_size, query_size, query_vec_size]), 输入
valid_lens: tensor([batch_size]), 序列中有效长度
output:
output: tensor([batch_size, query_size, hidden_vec_size]), 输出
"""
#1. Linear: queries, keys, values的线性变换, out shape: [batch_size, query_size, hidden_vec_size * head_num]
queries = self.W_q(queries)
keys = self.W_k(keys)
values = self.W_v(values)
# 2. score, shape: [batch_size * head_num, query_size, query_size]
queries = queries.reshape([-1, self.query_size, self.hidden_vec_size, self.head_num])\
.transpose((0, 3, 1, 2))\
.reshape([-1, self.query_size, self.hidden_vec_size])
keys = keys.reshape([-1, self.query_size, self.hidden_vec_size, self.head_num])\
.transpose((0, 3, 1, 2))\
.reshape([-1, self.query_size, self.hidden_vec_size])
values = values.reshape([-1, self.query_size, self.hidden_vec_size, self.head_num])\
.transpose((0, 3, 1, 2))\
.reshape([-1, self.query_size, self.hidden_vec_size])
scores = paddle.bmm(queries, keys.transpose((0, 2, 1))) / math.sqrt(self.hidden_vec_size)
scores = scores.reshape([-1, self.query_size])
# 3. mask, shape: [batch_size * head_num * query_size, query_size]
mask = paddle.arange(self.query_size, dtype=paddle.float32)[None, :] < paddle.repeat_interleave(valid_lens, self.query_size * self.head_num)[:, None]
scores[~mask] = float(-1e6)
# 4. softmax [batch_size, query_size * head_num, query_size]
scores = scores.reshape([-1, self.head_num, self.query_size, self.query_size])
scores = nn.functional.softmax(scores, axis=-1)
# 5. output [batch_size, query_size, head_num * hidden_vec_size]
z = paddle.bmm(scores.reshape([-1, self.query_size, self.query_size]), values)
z = z.reshape([-1, self.head_num, self.query_size, self.hidden_vec_size]).transpose((0, 2, 1, 3))
# 6. output linear
return self.W_o(z.reshape([-1, self.query_size, self.head_num * self.hidden_vec_size]))
4. 为什么要用注意力机制

按论文Attention Is All You Need的观点,上图为 self-attention同cnn、rnn在复杂度上的比较,其中n是指序列的长度,d是序列词向量的维度,k表示卷积核的大小,我们为什么将self-attention作为序列数据特征编码或解码器,主要基于三点理由:
- Complexity per Layer 计算量:计算量是指每层的计算量,可以看出当词向量的维度大于序列长度时,self-attention的计算量是要更小的。
- Sequential Operations 并行实现:self-attention完全可以通过矩阵运算来实现并行计算。
- Maximum Path Length 上下文依赖特征获取难易:比如序列中第1个词同最后1个词,上下文依赖特征获取难易是指要获取这两个词相互特征需要经过多少步,对于RNN网络需要经过序列长度的步,而对于CNN同卷积核和层数有关,对于self-attention只需要1步就能建立第1个词同最后1个词的关系。
版权归原作者 tostq 所有, 如有侵权,请联系我们删除。