传统语音增强——基本的维纳滤波语音降噪算法

一、维纳滤波的基本原理
基本维纳滤波就是用来解决从噪声中提取信号问题的一种过滤（或滤波）方法。它基于平稳随机过程模型，且假设退化模型为线性空间不变系统的。实际上这种线性滤波问题，可以看成是一种估计问题或一种线性估计问题。基本的维纳滤波是根据全部过去的和当前的观察数据来估计信号的当前值，它的解是以均方误差最小条件下所得到的系统的传递函数H（z）或单位样本响应h（n）的形式给出的，因此更常称这种系统为最佳线性过滤器或滤波器。设计维纳滤波器的过程就是寻求在最小均方误差下滤波器的单位样本响应h（n）或传递函数H（z）的表达式，其实质是解维纳-霍夫（Wiener-Hopf）方程。

设带噪语音信号为x(n)=s(n)+v(n)
其中，x（n)表示带噪信号；v（n)表示噪声。则经过维纳滤波器h（n)的输出响应y（n)为

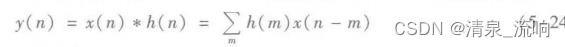
理论上，x（n)通过线性系统h（n）后得到的y（n)应尽量接近于s（n)，因此y（n)为s（n)
的估计值，可用 表示，即

从上式可知，卷积形式可以理解为从当前和过去的观察值x（n)，x（n-1)，x（n-2）…x（n-m），…来估计信号的当前值。因此，用h（n）进行滤波实际上是一种统计估计问题。

按最小均方误差准则使和s（n）的均方误差ξ=E[e^2（n）]=E[{s（n）-}^2]
达到最小。使ξ最小的充要条件是ξ对于h（n）的偏导数为零，即

上式整理可得

这就是正交性原理或投影原理。可得

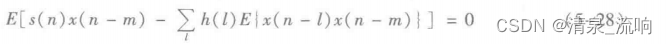
已知，s（n)和d（n)是联合宽平稳的，因此令x（n)的自相关函数Rx(m-l)=E{x（n-m)x(n-l)}，s(n)与x(n)的互相关函数Rsx（m)=E{s（n)x(n-m)}，则上式可变为

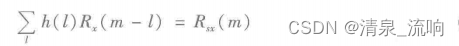
上式称为维纳滤波器的标准方程或维纳-霍夫（Wiener-Hopf）方程。如果已知Rsx（m）和Rx（m-l），那么解此方程即可求得维纳滤波器的冲激响应。

当l从0到N-1取有限个整数值时，设滤波器冲激响应序列的长度为N，冲激响应矢量为

滤波器输入数据矢量为

则滤波器的输出为

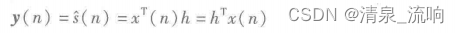
这样，上式所示的维纳-霍夫方程可写成Q = Rh
其中，Q=E[x（n)s（n)]是s（n)与x（n)的互相关函数，它是一个N维列矢量；R是x（n)的自相关函数，是N阶方阵R=E[x（n)x^T（n)]，则最优的维纳滤波器的冲激响应为hopt=R^(-1)Q

如果进行傅里叶变换可得

式中，Px（k)为x（n)的功率谱密度；Psx（k)为x（n)与s（n)的互功率谱密度。
由于v（n)与s（n)互不相关，即Rsv（k)=0，则可得

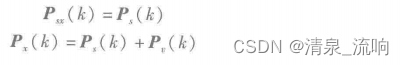
此时，上可变为

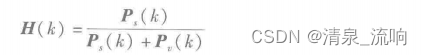
该式为维纳滤波器的谱估计器。此时，的频谱估计值为

此外，H（k）还可以写为

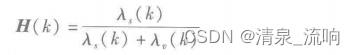
式中，λs（k）和λv（k）分别为第k个频点上的信号和噪声的功率谱。
传统的维纳滤波法需要估计出纯净语音信号的功率谱，一般用类似谱减法的方法得到，
即用带噪语音功率谱减去估计到的噪声功率谱，这种方法会存在残留噪声大的问题。

二、维纳滤波语音增强实验

基本维纳滤波函数Weina_Norm

名称：Weina_Norm
功能：基本维纳滤波算法。
调用格式：
enhanced = Weina_Norm(x, wind, inc, NIS,alpha,beta)
说明：输入参数x是输入的含噪语音信号；wlen为窗函数或窗长；inc是帧移；NIS是前导无话段帧数；alpha和beta是谱减法的参数。enhanced是降噪后的信号。

函数程序如下：

% 维纳滤波 enhanced=Weina_Norm(x,wind,inc,NIS,alpha,beta)
% MS估计噪声功率谱,需要估计纯净信号功率Ps
% x:输入语音信号
% framesize:帧长
% overlap:帧重叠长度
% NIS：无声帧帧数
% alpha,beta:抑制参数
% ---------------------------------------------------------------------------------------------------------------
 %%
function enhanced=Weina_Norm(x,wind,inc,NIS,alpha,beta)
    nwin=length(wind);           % 取窗长
    if (nwin == 1)              % 判断窗长是否为1，若为1，即表示没有设窗函数
       framesize= wind;               % 是，帧长=win
       wnd=hamming(framesize);                      % 设置窗函数
    else
       framesize = nwin;              % 否，帧长=窗长
       wnd=wind;
    end
    
    y=enframe(x,wnd,inc)';             % 分帧
    framenum=size(y,2);                           % 求帧数
    y_fft = fft(y);                         % FFT
    y_a = abs(y_fft);                       % 求取幅值
    y_phase=angle(y_fft);                   % 求取相位角
    y_a2=y_a.^2;                            % 求能量
    noise=mean(y_a2(:,1:NIS),2);               % 计算噪声段平均能量
    signal=zeros(framesize,1);
    for i=1:framenum
         frame=y(:,i);                                 %取一帧数据
         y_fft=fft(frame);                 %对信号帧y_ham进行短时傅立叶变换,得到频域信号y_fft
         y_fft2=abs(y_fft).^2;     %计算频域信号y_fft每帧的功率谱y_w
     
         %带噪语音谱减去噪声谱
         for k=1:framesize
                if   abs( y_fft2(k) )  >=alpha*noise(k)%(k,i)
                      signal(k)=y_fft2(k)-alpha*noise(k);%(k,i);
                      if signal(k)<0
                          signal(k)=0;
                      end
                else
                      signal(k)=beta*noise(k);%*0.01;
                end
                
         end
         %计算H(W)
         Hw=( signal./(signal+1*noise) ).^1 ;
         %维纳滤波器输出
         yw(:,i)=Hw.*y_fft;
         yt(:,i)=ifft(yw(:,i));
    end
  %采用相位，反而信噪比低
    enhanced=filpframe(yt',wnd,inc);

信噪比计算函数SNR_Calc

名称：SNR_Calc
功能：计算信噪比。
调用格式：
snr=SNR_Calc(x,xn)

说明：输入信号x是输入的纯净语音信号；xn是输入的含噪信号。输出参数snr是计算的信噪比。

函数程序如下：

function snr=SNR_Calc(I,In)
% 计算带噪语音信号的信噪比
% I 是纯语音信号
% In 是带噪的语音信号
% 信噪比计算公式是
% snr=10*log10(Esignal/Enoise)
I=I(:)';                             % 把数据转为一列
In=In(:)';
Ps=sum((I-mean(I)).^2);              % 信号的能量
Pn=sum((I-In).^2);                      % 噪声的能量
snr=10*log10(Ps/Pn);                 % 信号的能量与噪声的能量之比，再求分贝值

案例、用基本的维纳滤波算法给语音减噪

程序如下：

clear all; clc; close all;

[xx, fs] = audioread('C5_3_y.wav');           % 读入数据文件
xx=xx-mean(xx);                         % 消除直流分量
x=xx/max(abs(xx));                      % 幅值归一化
IS=0.25;                                % 设置前导无话段长度
wlen=200;                               % 设置帧长为25ms
inc=80;                                 % 设置帧移为10ms
SNR=5;                                  % 设置信噪比SNR
NIS=fix((IS*fs-wlen)/inc +1);           % 求前导无话段帧数
alpha=2;
beta=0.01;
signal=awgn(x,SNR,'measured','db');               % 叠加噪声
output=Weina_Norm(x,wlen,inc,NIS,alpha,beta) ;
output=output/max(abs(output));
len=min(length(output),length(x));
x=x(1:len);
signal=signal(1:len);
output=output(1:len);

snr1=SNR_Calc(x,signal);            % 计算初始信噪比
snr2=SNR_Calc(x,output);            % 计算降噪后的信噪比
snr=snr2-snr1;
fprintf('snr1=%5.4f   snr2=%5.4f   snr=%5.4f\n',snr1,snr2,snr);

% 作图
time=(0:len-1)/fs;                        % 设置时间
subplot 311; plot(time,x,'k'); grid; axis tight;
title('纯语音波形'); ylabel('幅值')
subplot 312; plot(time,signal,'k'); grid; axis tight;
title(['带噪语音 信噪比=' num2str(SNR) 'dB']); ylabel('幅值')
subplot 313; plot(time,output,'k');grid;%hold on;
title('滤波后波形'); ylabel('幅值'); xlabel('时间/s');

运行结果如下：

实验使用到的语音数据下载链接如下：

传统语音增强——最小方均(LMS)自适应滤波算法-数据集文档类资源-CSDN下载

参考文献：语音信号处理实验教程；梁瑞宇、赵力、魏昕（编著）