
个人主页:****欢迎来到 Papicatch的博客
** 课设专栏 :**学生成绩管理系统
**专业知识专栏: **专业知识

🍉引言
在当今科技飞速发展的时代,人工智能已然成为了引领变革的关键力量。其中,反向传播算法作为人工智能神经网络训练的核心机制,对于推动人工智能的进步发挥着举足轻重的作用。
回顾人工智能的发展历程,从早期的理论探索到如今广泛的实际应用,每一次的突破都离不开算法的创新与优化。而反向传播算法的出现,无疑是其中的一个重要里程碑。
它不仅使得神经网络能够处理更为复杂和庞大的数据,还极大地提高了模型的学习能力和预测精度。然而,如同任何技术一样,反向传播算法也并非完美无缺,在实际应用中仍面临着诸多挑战和问题。
在接下来的内容中,我们将深入探讨人工智能反向传播算法的方方面面,包括其原理、应用、优势以及局限性等,以期为读者呈现一个全面而深入的理解。
🍉反向传播

🍈定义
反向传播(Backpropagation)是一种在人工神经网络中用于计算误差梯度并据此调整网络参数(如权重和偏置)的数学算法。
在神经网络中,数据从输入层经过一系列隐藏层的处理,最终在输出层产生输出。然后,将输出与期望的目标值进行比较,得到误差。
反向传播的核心在于利用微积分中的链式法则,从输出层开始,逐层向后计算误差对于每个神经元的输入的梯度。这些梯度反映了参数的微小变化对误差的影响程度。
具体来说,对于每一个神经元,反向传播计算其输出值相对于其输入值(包括与前一层神经元连接的权重和偏置)的偏导数。这个过程从输出层开始,依次反向传播到隐藏层,直至输入层。
通过这种方式,网络中的每一个权重和偏置都能得到一个对应的梯度值。这些梯度值用于指导如何调整权重和偏置,以减小误差,从而使得神经网络在经过多次训练迭代后,能够对新的输入数据做出更准确的预测或分类。
🍈反向传播的作用
** 反向传播在人工神经网络的训练中具有极其重要的作用,主要体现在以下几个方面:**
🍍参数优化
- 神经网络的性能很大程度上取决于权重和偏置等参数的取值。反向传播通过计算误差对这些参数的梯度,为优化算法(如随机梯度下降)提供了方向和步长的信息,使得参数能够朝着减小误差的方向调整。
- 例如,在一个用于图像识别的卷积神经网络中,通过反向传播计算出每个卷积核的权重梯度,从而调整卷积核的参数,以提高对不同图像特征的提取能力。
🍍学习复杂模式
- 现实世界中的数据往往具有复杂的内在模式和关系。反向传播使得神经网络能够自动从大量的数据中学习到这些模式。
- 比如在自然语言处理中,通过反向传播,网络可以学习到单词之间的语义关系、语法结构等复杂的语言模式,从而能够进行文本分类、机器翻译等任务。
🍍提高泛化能力
- 良好的泛化能力意味着模型能够对未见过的数据做出准确的预测。反向传播在训练过程中不断调整参数,使得模型能够捕捉到数据的一般规律,而不仅仅是记住训练数据的特定细节,从而提高模型在新数据上的表现。
- 假设一个用于预测股票价格的神经网络,通过反向传播在历史数据上进行训练,模型能够学习到影响股票价格的普遍因素,而不是仅仅适应特定时间段的价格走势,从而在新的市场情况下也能做出相对准确的预测。
🍍构建深度网络
- 随着计算能力的提高和算法的改进,深度神经网络在处理复杂任务上表现出色。反向传播为训练深度网络提供了可行的方法,使得误差能够有效地在多层网络中传播和调整参数。
- 例如,在图像识别的深度残差网络中,反向传播能够确保信息在多层传递过程中的准确性和有效性,从而使网络能够学习到更高级和抽象的特征。
🍍适应大规模数据
- 当今的数据量越来越大,反向传播能够高效地处理大规模的数据训练。通过梯度计算和参数更新,网络能够从海量数据中挖掘有用的信息。
- 像在互联网搜索引擎的排序算法中,基于反向传播的神经网络可以利用大量的用户点击数据来学习最优的排序模型,以提供更准确和相关的搜索结果。
🍈工作原理
反向传播是一种用于训练人工神经网络的算法,其工作原理基于微积分中的链式法则。
首先,在神经网络的前向传播阶段,输入数据通过网络的各层,经过一系列线性和非线性变换得到输出。
假设神经网络有 L 层,对于第 ι 层的神经元,其输入为 zι ,输出为 aι 。
** 前向传播的计算过程为:**

其中,ωι 是第 ι 层的权重矩阵,bι 是偏置向量,σ 是激活函数。
接下来是反向传播阶段。首先计算输出层的误差。假设损失函数为 C ,对于输出层的神经元,误差 δι 为:

其中,⊙ 表示元素相乘,σ ‘ 是激活函数的导数。
然后,从输出层开始,逐层反向计算误差。对于第 ι 层的误差 δι ,其计算公式为:

有了误差之后,就可以计算权重和偏置的梯度。对于权重 ωι 的梯度为:

对于偏置 bι 的梯度为:

最后,根据计算得到的梯度,使用优化算法(如随机梯度下降)来更新权重和偏置:

其中,α 是学习率。
例如,假设有一个简单的三层神经网络,输入层有两个神经元,隐藏层有三个神经元,输出层有一个神经元。在前向传播中,输入数据经过计算得到输出。然后,将输出与真实值比较得到误差。在反向传播中,先计算输出层的误差,然后根据公式依次计算隐藏层的误差,进而得到权重和偏置的梯度,进行参数更新。通过多次这样的前向传播和反向传播的迭代,网络逐渐学习到最优的参数,以提高预测的准确性。
综上所述,反向传播通过从输出层向输入层逐层计算误差的梯度,实现了对神经网络参数的有效调整和优化。
🍈数学原理
反向传播的数学原理基于微积分中的链式法则。
考虑一个简单的多层神经网络,假设具有 L 层,第 层有
个神经元。
对于第 层的第
个神经元,其输入为:

其中, 是第
层的第
个神经元的输出,
是连接第
层的第
个神经元和第
层的第
个神经元的权重,
是第
层的第
个神经元的偏置。
经过激活函数 得到输出:

设损失函数为 ,我们的目标是最小化这个损失函数。
在反向传播中,我们要计算损失函数对每个权重和偏置的梯度。
对于输出层(第 层),误差
为:

对于中间层(),误差
为:

接下来计算权重和偏置的梯度:
权重 的梯度:

偏置 的梯度:

以一个具体的例子来说明。假设有一个二层神经网络,输入层有两个神经元,隐藏层有两个神经元,输出层有一个神经元。
输入层到隐藏层的权重分别为 ,,,,隐藏层的偏置分别为:、。。隐藏层到输出层的权重分别为 :、,输出层的偏置为:。假设输入为 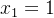,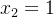,激活函数为 sigmoid 函数 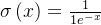 ,损失函数为均方误差,假设目标值 。
前向传播计算:
隐藏层的输入:

隐藏层的输出:

输出层的输入:

输出层的输出:

计算误差:

反向传播计算:
输出层的误差:

隐藏层的误差:

权重和偏置的梯度:

通过这样的计算,可以根据梯度使用优化算法(如随机梯度下降)来更新权重和偏置,以不断优化神经网络的性能。
🍈应用场景
🍍图像识别
- 例如人脸识别、物体检测和分类等任务。通过反向传播调整神经网络的参数,使其能够学习到不同图像的特征,从而准确识别图像中的内容。
🍍语音识别
- 帮助模型学习语音信号的特征和模式,实现对语音的准确转录和理解。
🍍自然语言处理
- 包括文本分类、情感分析、机器翻译等。模型可以通过反向传播理解语言的结构和语义信息。
🍍医疗诊断
- 分析医学影像(如 X 光、CT 扫描)、预测疾病风险等。
🍍金融预测
- 如股票价格预测、信用评估等,基于历史数据进行学习和预测。
🍈反向传播的优势
🍍强大的学习能力
- 能够处理大规模、高维度的数据,自动提取复杂的特征和模式。
🍍适应性强
- 可以应用于各种不同类型的任务和数据,只需适当调整网络结构和参数。
🍍精度高
- 经过充分训练,能够达到较高的预测和分类精度。
🍍自动化特征工程
- 无需手动设计特征,模型自身能够学习到最有效的特征表示。
🍈反向传播的局限性
🍍计算资源需求高
- 特别是对于大型复杂的神经网络,训练过程需要大量的计算时间和内存。
🍍梯度消失和梯度爆炸
- 在深度网络中,可能出现梯度在反向传播过程中逐渐减小为零(梯度消失)或迅速增大(梯度爆炸),导致训练困难。
🍍过拟合
- 容易对训练数据过度拟合,导致在新数据上的表现不佳。
🍍解释性差
- 难以解释模型是如何做出决策和生成输出的,使得其在一些对可解释性要求高的场景中应用受限。
🍍对数据质量敏感
- 数据中的噪声和偏差可能会对训练结果产生较大影响。
🍈代码实现
import numpy as np
class NeuralNetwork:
def __init__(self, input_dim, hidden_dim, output_dim):
self.input_dim = input_dim
self.hidden_dim = hidden_dim
self.output_dim = output_dim
# 随机初始化权重
self.W1 = np.random.randn(input_dim, hidden_dim)
self.b1 = np.zeros(hidden_dim)
self.W2 = np.random.randn(hidden_dim, output_dim)
self.b2 = np.zeros(output_dim)
def sigmoid(self, z):
return 1 / (1 + np.exp(-z))
def forward_propagation(self, X):
self.z1 = np.dot(X, self.W1) + self.b1
self.a1 = self.sigmoid(self.z1)
self.z2 = np.dot(self.a1, self.W2) + self.b2
self.a2 = self.sigmoid(self.z2)
return self.a2
def back_propagation(self, X, y):
m = X.shape[0]
# 计算输出层的误差
dZ2 = self.a2 - y
dW2 = np.dot(self.a1.T, dZ2) / m
db2 = np.sum(dZ2, axis=0, keepdims=True) / m
# 计算隐藏层的误差
dZ1 = np.dot(dZ2, self.W2.T) * (self.a1 * (1 - self.a1))
dW1 = np.dot(X.T, dZ1) / m
db1 = np.sum(dZ1, axis=0, keepdims=True) / m
return dW1, db1, dW2, db2
def update_parameters(self, dW1, db1, dW2, db2, learning_rate):
self.W1 -= learning_rate * dW1
self.b1 -= learning_rate * db1
self.W2 -= learning_rate * dW2
self.b2 -= learning_rate * db2
def train(self, X, y, epochs, learning_rate):
for epoch in range(epochs):
output = self.forward_propagation(X)
dW1, db1, dW2, db2 = self.back_propagation(X, y)
self.update_parameters(dW1, db1, dW2, db2, learning_rate)
if epoch % 100 == 0:
loss = np.mean((output - y) ** 2)
print(f'Epoch {epoch}, Loss: {loss}')
# 示例用法
X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
y = np.array([[0], [1], [1], [0]])
nn = NeuralNetwork(2, 3, 1)
nn.train(X, y, epochs=1000, learning_rate=0.1)
🍍代码分析
class NeuralNetwork:
def __init__(self, input_dim, hidden_dim, output_dim):
self.input_dim = input_dim
self.hidden_dim = hidden_dim
self.output_dim = output_dim
# 随机初始化权重
self.W1 = np.random.randn(input_dim, hidden_dim)
self.b1 = np.zeros(hidden_dim)
self.W2 = np.random.randn(hidden_dim, output_dim)
self.b2 = np.zeros(output_dim)
定义了
NeuralNetwork
类,在初始化方法
__init__
中:
- 接收输入维度
input_dim、隐藏层维度hidden_dim和输出维度output_dim作为参数。- 使用
np.random.randn随机初始化输入层到隐藏层的权重W1和隐藏层到输出层的权重W2。- 使用
np.zeros初始化隐藏层偏置b1和输出层偏置b2为零向量。
def sigmoid(self, z):
return 1 / (1 + np.exp(-z))
定义了
sigmoid
激活函数,用于对神经元的输入进行非线性变换。
def forward_propagation(self, X):
self.z1 = np.dot(X, self.W1) + self.b1
self.a1 = self.sigmoid(self.z1)
self.z2 = np.dot(self.a1, self.W2) + self.b2
self.a2 = self.sigmoid(self.z2)
return self.a2
forward_propagation
方法实现前向传播过程:
- 计算输入层到隐藏层的线性变换结果
z1,并通过sigmoid函数得到隐藏层的激活输出a1。- 基于
a1计算隐藏层到输出层的线性变换结果z2,再通过sigmoid函数得到输出层的激活输出a2,并返回a2。
def back_propagation(self, X, y):
m = X.shape[0]
# 计算输出层的误差
dZ2 = self.a2 - y
dW2 = np.dot(self.a1.T, dZ2) / m
db2 = np.sum(dZ2, axis=0, keepdims=True) / m
# 计算隐藏层的误差
dZ1 = np.dot(dZ2, self.W2.T) * (self.a1 * (1 - self.a1))
dW1 = np.dot(X.T, dZ1) / m
db1 = np.sum(dZ1, axis=0, keepdims=True) / m
return dW1, db1, dW2, db2
back_propagation
方法实现反向传播过程:
- 首先获取样本数量
m。- 计算输出层的误差
dZ2,然后根据误差计算输出层权重和偏置的梯度dW2和db2。- 通过输出层的误差计算隐藏层的误差
dZ1,进而得到隐藏层权重和偏置的梯度dW1和db1,最后返回这些梯度。
def update_parameters(self, dW1, db1, dW2, db2, learning_rate):
self.W1 -= learning_rate * dW1
self.b1 -= learning_rate * db1
self.W2 -= learning_rate * dW2
self.b2 -= learning_rate * db2
update_parameters
方法根据反向传播得到的梯度和学习率更新权重和偏置。
def train(self, X, y, epochs, learning_rate):
for epoch in range(epochs):
output = self.forward_propagation(X)
dW1, db1, dW2, db2 = self.back_propagation(X, y)
self.update_parameters(dW1, db1, dW2, db2, learning_rate)
if epoch % 100 == 0:
loss = np.mean((output - y) ** 2)
print(f'Epoch {epoch}, Loss: {loss}')
train
方法用于训练神经网络:
- 在每次迭代中,进行前向传播得到输出,然后进行反向传播得到梯度,最后更新参数。
- 每隔 100 个 epoch 计算并打印均方误差损失。
# 示例用法
X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
y = np.array([[0], [1], [1], [0]])
nn = NeuralNetwork(2, 3, 1)
nn.train(X, y, epochs=1000, learning_rate=0.1)
在示例用法中,定义了输入数据
X
和目标输出
y
,创建了神经网络对象
nn
,并调用
train
方法进行 1000 次迭代的训练,学习率设置为 0.1。
🍉示例
🍈代码实现
import numpy as np
class NeuralNetwork:
def __init__(self, input_dim, hidden_dim, output_dim):
"""
初始化神经网络的参数
参数:
input_dim (int): 输入层的维度
hidden_dim (int): 隐藏层的维度
output_dim (int): 输出层的维度
"""
self.input_dim = input_dim
self.hidden_dim = hidden_dim
self.output_dim = output_dim
# 随机初始化权重
self.W1 = np.random.randn(input_dim, hidden_dim)
self.b1 = np.zeros(hidden_dim)
self.W2 = np.random.randn(hidden_dim, output_dim)
self.b2 = np.zeros(output_dim)
def sigmoid(self, z):
"""
Sigmoid 激活函数
参数:
z (ndarray): 输入值
返回:
ndarray: Sigmoid 激活后的结果
"""
return 1 / (1 + np.exp(-z))
def forward_propagation(self, X):
"""
前向传播
参数:
X (ndarray): 输入数据
返回:
ndarray: 前向传播的输出结果
"""
self.z1 = np.dot(X, self.W1) + self.b1
self.a1 = self.sigmoid(self.z1)
self.z2 = np.dot(self.a1, self.W2) + self.b2
self.a2 = self.sigmoid(self.z2)
return self.a2
def back_propagation(self, X, y):
"""
反向传播计算梯度
参数:
X (ndarray): 输入数据
y (ndarray): 真实标签
返回:
tuple: 包含隐藏层和输出层的权重和偏置梯度
"""
m = X.shape[0] # 样本数量
# 计算输出层的误差
dZ2 = self.a2 - y
dW2 = np.dot(self.a1.T, dZ2) / m
db2 = np.sum(dZ2, axis=0, keepdims=True) / m
# 计算隐藏层的误差
dZ1 = np.dot(dZ2, self.W2.T) * (self.a1 * (1 - self.a1))
dW1 = np.dot(X.T, dZ1) / m
db1 = np.sum(dZ1, axis=0, keepdims=True) / m
return dW1, db1, dW2, db2
def update_parameters(self, dW1, db1, dW2, db2, learning_rate):
"""
根据梯度更新参数
参数:
dW1 (ndarray): 隐藏层权重梯度
db1 (ndarray): 隐藏层偏置梯度
dW2 (ndarray): 输出层权重梯度
db2 (ndarray): 输出层偏置梯度
learning_rate (float): 学习率
"""
self.W1 -= learning_rate * dW1
self.b1 -= learning_rate * db1
self.W2 -= learning_rate * dW2
self.b2 -= learning_rate * db2
def train(self, X, y, epochs, learning_rate):
"""
训练神经网络
参数:
X (ndarray): 输入数据
y (ndarray): 真实标签
epochs (int): 训练轮数
learning_rate (float): 学习率
"""
for epoch in range(epochs):
output = self.forward_propagation(X)
dW1, db1, dW2, db2 = self.back_propagation(X, y)
self.update_parameters(dW1, db1, dW2, db2, learning_rate)
if epoch % 100 == 0:
loss = np.mean((output - y) ** 2)
print(f'Epoch {epoch}, Loss: {loss}')
# 示例用法
X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
y = np.array([[0], [1], [1], [0]])
nn = NeuralNetwork(2, 3, 1)
nn.train(X, y, epochs=1000, learning_rate=0.1)
🍈代码分析
NeuralNetwork
类用于构建和训练一个简单的两层神经网络。
__init__方法初始化网络的结构和随机生成权重和偏置。sigmoid函数定义了 Sigmoid 激活函数,用于引入非线性。forward_propagation执行前向传播计算,依次计算各层的线性组合和激活输出。back_propagation进行反向传播,根据输出层的误差逐步计算各层的梯度。update_parameters依据计算得到的梯度和学习率更新权重和偏置。train方法执行训练过程,在每一轮中进行前向传播、反向传播和参数更新,并定期打印损失值。
在示例用法中,我们定义了简单的输入数据
X
和目标标签
y
,创建了神经网络对象
nn
,并使用指定的学习率和训练轮数进行训练。通过观察每 100 轮的损失值,可以了解训练过程中模型的性能改进情况。
🍉总结
反向传播是人工智能中神经网络训练的核心算法,具有至关重要的作用。
它通过巧妙地运用微积分中的链式法则,从输出层开始,将误差逐层反向传播至输入层,从而计算出网络中各个参数(如权重和偏置)对于误差的梯度。
反向传播的主要优势在于能够高效地优化神经网络的参数,使网络能够从大量的数据中自动学习到有用的特征和模式,从而在图像识别、语音处理、自然语言处理等众多领域取得出色的表现。
然而,反向传播并非完美无缺。在实际应用中,它面临着一些挑战,如计算资源需求大、可能出现梯度消失或爆炸问题、容易过拟合以及模型解释性差等。
尽管存在局限性,反向传播仍然是推动人工智能发展的关键技术之一,研究人员不断探索和改进,以克服其不足,进一步提升神经网络的性能和应用效果。

版权归原作者 Papicatch 所有, 如有侵权,请联系我们删除。