1. 什么是指数分布
设随机变量X具有如下形式的密度函数，那么则称X服从参数为θ的指数分布, 记为X~EXP(θ).
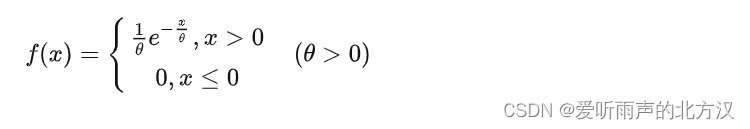
** 指数分布的分布函数为：**
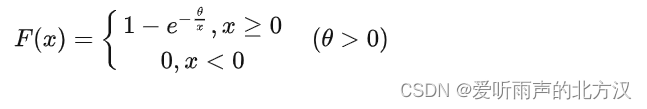
2. 指数分布的期望和方差
①数学期望
如果X 服从参数为λ (λ>0)的指数分布,那么指数分布X~EXP(θ)的数学期望： λ
②方差
设X 服从参数为λ (λ>0)的指数分布,指数分布X~EXP(θ)的方差：λ^2。
总结一下，我们经常遇到的指数分布、均匀分布和正态分布的概率密度函数与图形如下：
本文转载自: https://blog.csdn.net/qq_25018077/article/details/127087195
版权归原作者 爱听雨声的北方汉 所有， 如有侵权，请联系我们删除。
版权归原作者 爱听雨声的北方汉 所有， 如有侵权，请联系我们删除。