模型评估：可决系数与纳什效率系数

1、可决系数 R2

  可决系数（Coefficient of determination，R）是用来度量一个统计模型的拟合优度的。其数学表达式如下：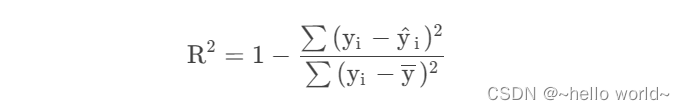

式中：yi 是变量观测值；

      y 
     
    
      ‾ 
     
    
   
  
    \overline{y} 
   
  
y​ 是变量观测值的均值；

 
  
   
    
     
     
       y 
      
     
       ^ 
      
     
    
      i 
     
    
   
  
    \hat{y}_i 
   
  
y^​i​ 是统计模型的变量模拟值；

   R2 的取值范围为[0,1]。

2、纳什效率系数 NSE

   纳什效率系数（Nash-Sutcliffe Efficiency, NSE）常用于用于量化模拟模型（如水文模型）的预测精度。其数学表达式如下：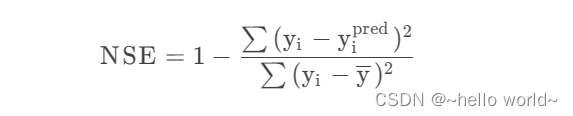

式中：yipred 是预测模型对变量的预测值。预测值属于回归样本外得到的预测结果，和回归模型的模拟值有很大区别，模型误差的平方和 ( yi− yipred)2 可能大于总平方和 ( yi−

      y 
     
    
      ‾ 
     
    
   
  
    \overline{y} 
   
  
y​ )2 ，对于一个完美的模型，估计的误差的方差等于0，则 NSE=1；相反，一个模型产生的估计误差方差等于观察到的时间序列的方差，结果 NSE=0。实际上，NSE=0表示该模型具有与时间序列平均值相同的预测能力，即误差平方和。当预测模型得到的估计误差方差显著大于观测值方差时，NSE<0。NSE值越接近1，表明模型预测能力越好。因此NSE的取值范围为 (- 
 
  
   
   
     ∞ 
    
   
  
    \infty 
   
  
∞, 1]。

   但是，如果将NSE用于模型回归中，则和 R2 完全等价，范围是[0,1]。