10.1 概率建模
模型描述了世界的（一部分）运作方式。
模型总是简化的：
- 可能没有考虑到每个变量，不关心或者无法为其建模。
- 可能没有考虑到变量之间的所有相互作用，无法发现或者代价昂贵。
- 所有的模型都是错的；但有些是有用的。
在<人工智能学习（七）：概率>中，我们主要谈论了动作，选择动作，动作序列，链式推理。但是在这一篇博文，我们要讨论的不是动作而是关于信念度。我们希望描述的是世界的某些部分，我们关心的变量是如何工作的。
我们用概率模型做什么？
我们（或我们的代理）需要通过给定证据对未知变量进行推理。
- 解释（诊断性推理）
- 预测（因果推理）
- 信息的价值
10.1.1 独立性
如果两个变量是独立的：
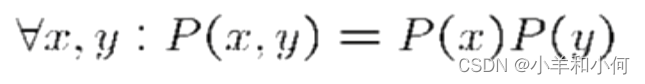
注意：公式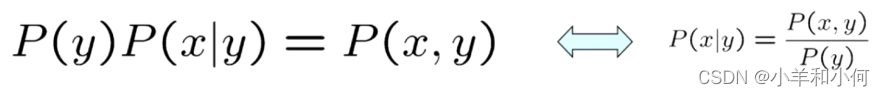 
是普适的，而上面的公式有一个前提条件是两个变量相互独立，并不是普适的。
这就是说，他们的联合分布是由两个更简单的分布组成的产物。
另一种形式：
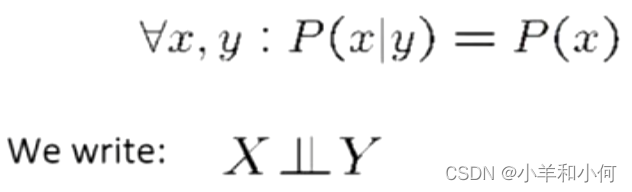
独立性是一个简化的建模假设：经验性的联合分布：最多 "接近 "独立。不存在完美的独立性。
通过计算发现不相等，我们可以说和
是不独立的两个变量：
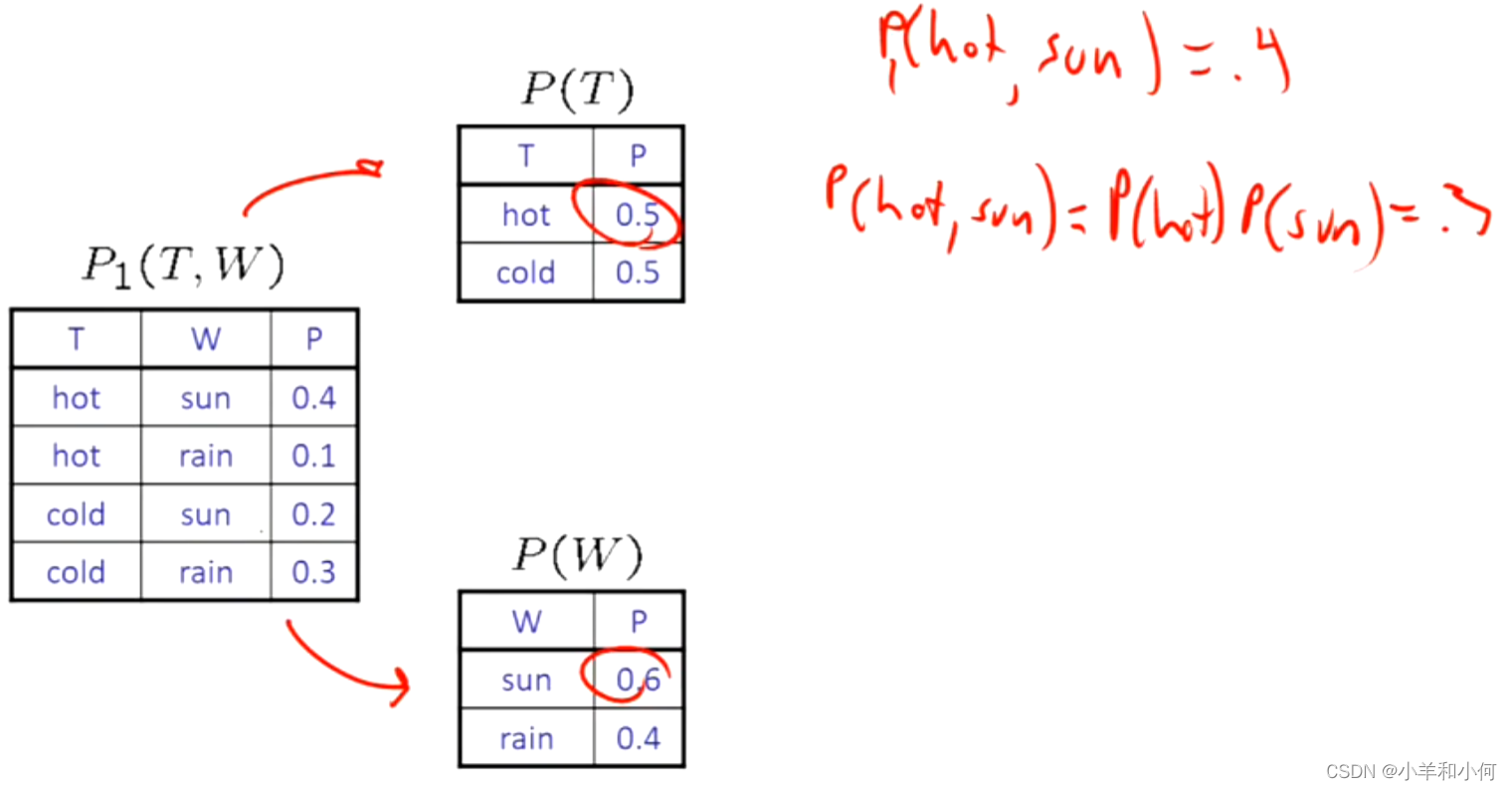
下面通过计算就满足独立性：
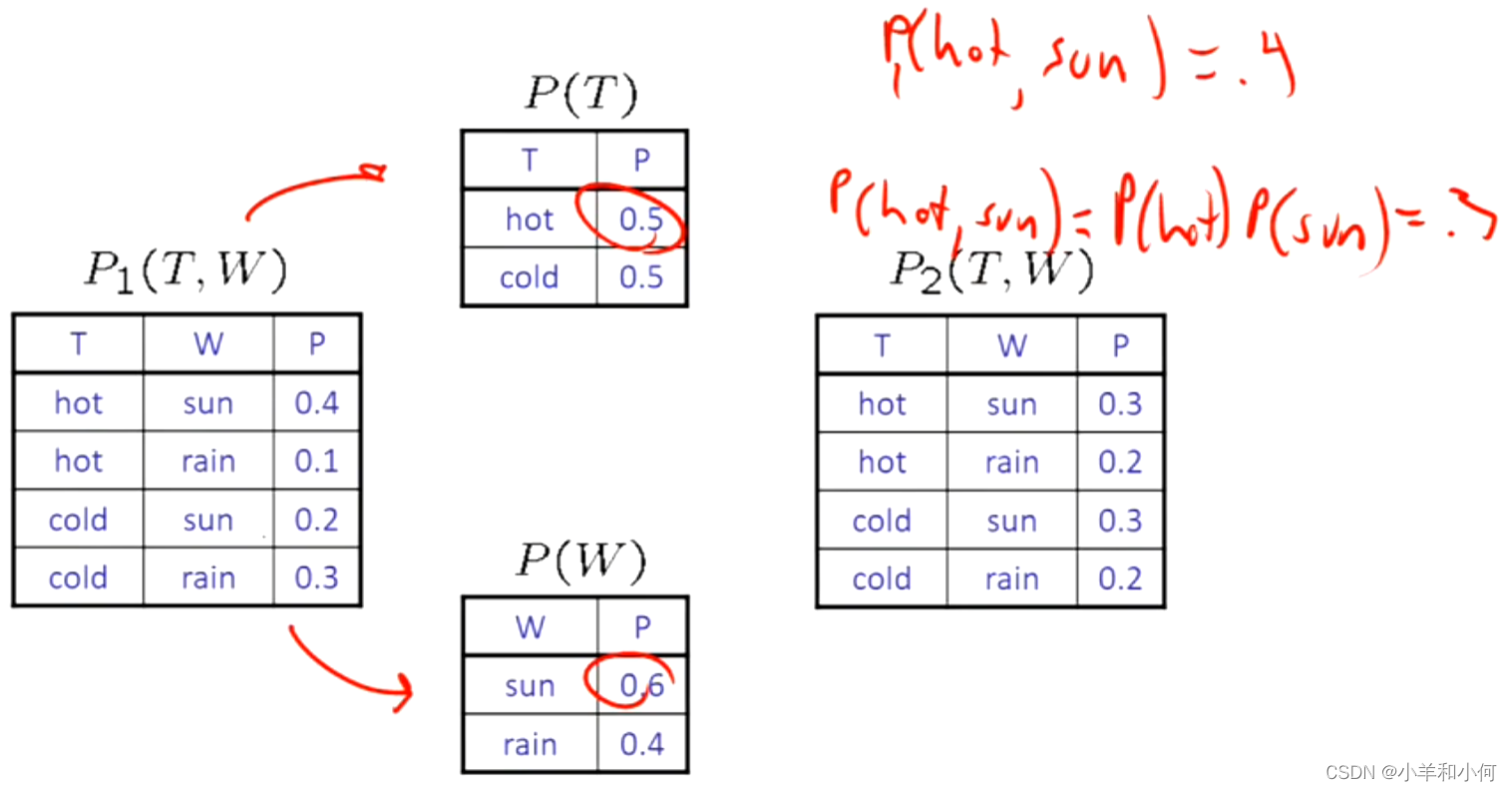
一个极端的例子，如果我们通过抛枚硬币，我们不需要写出指数级的联合分布表，只需要写出单个的概率表，因为变量之间是相互独立的。如果你问我任何有关联合分布的问题，我都可以通过将变量相乘得到答案。更加极端的说，其实我们可以给出更紧凑的表，一个表就可以代表所有东西，因为它们都是相同的。
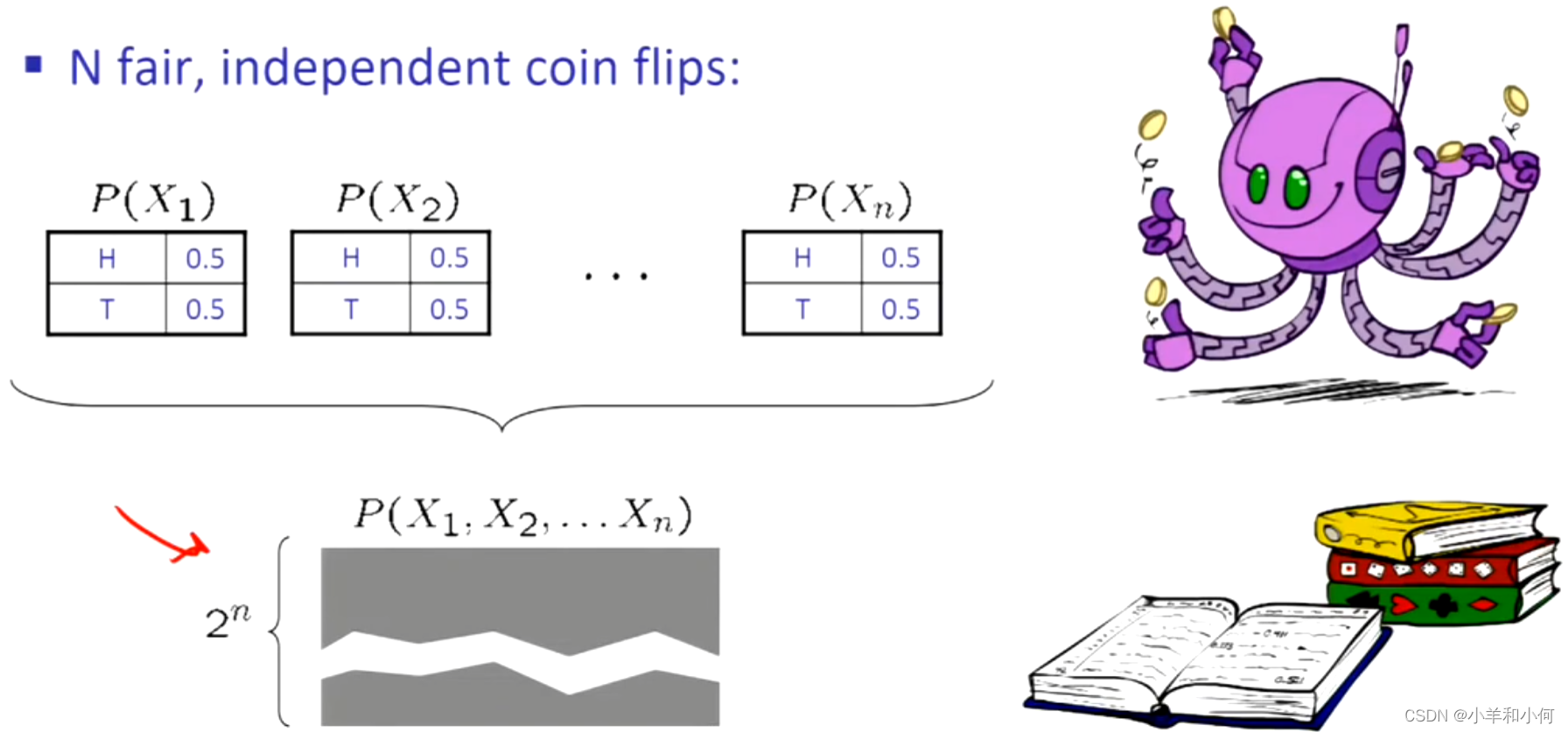
10.1.2 条件独立
在条件独立中，我们不会说两个变量没有交互作用。我们说它们的互动在某种程度上是由另一个变量介导的。
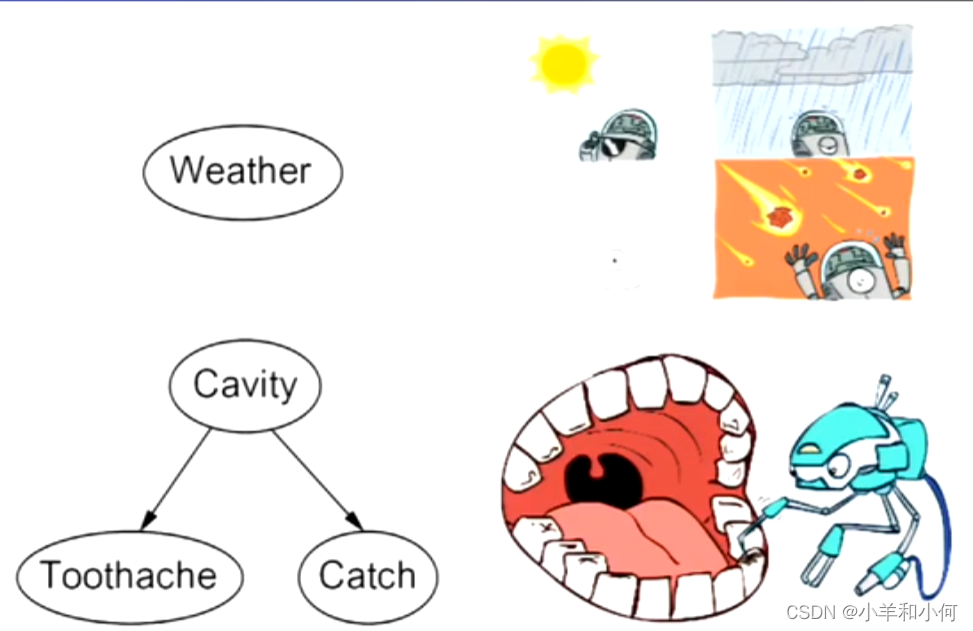
如果我有一个蛀牙（），探针卡（
）在里面的概率并不取决于我是否有牙痛：
如果没有蛀牙，同样的独立性也是成立的：
以上两个例子是说明，一旦了解了蛀牙，我就了解了是否卡住需要注意的所有问题，牙齿疼痛就不再重要了。这是独立吗？并不是，我们只能说随机变量，给定蛀牙（有条件的），独立于牙齿疼痛。是否卡住有条件的独立于牙痛。
Equivalent statements：
一个可以很容易地从另一个导出。
无条件（绝对）独立性非常罕见。
有条件的独立性是我们对不确定环境的最基本和最有力的知识形式。
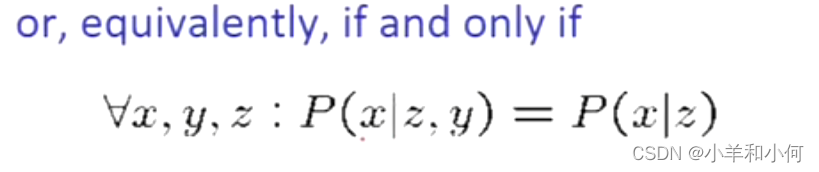
交通情况和雨伞在给定下雨的条件下独立：
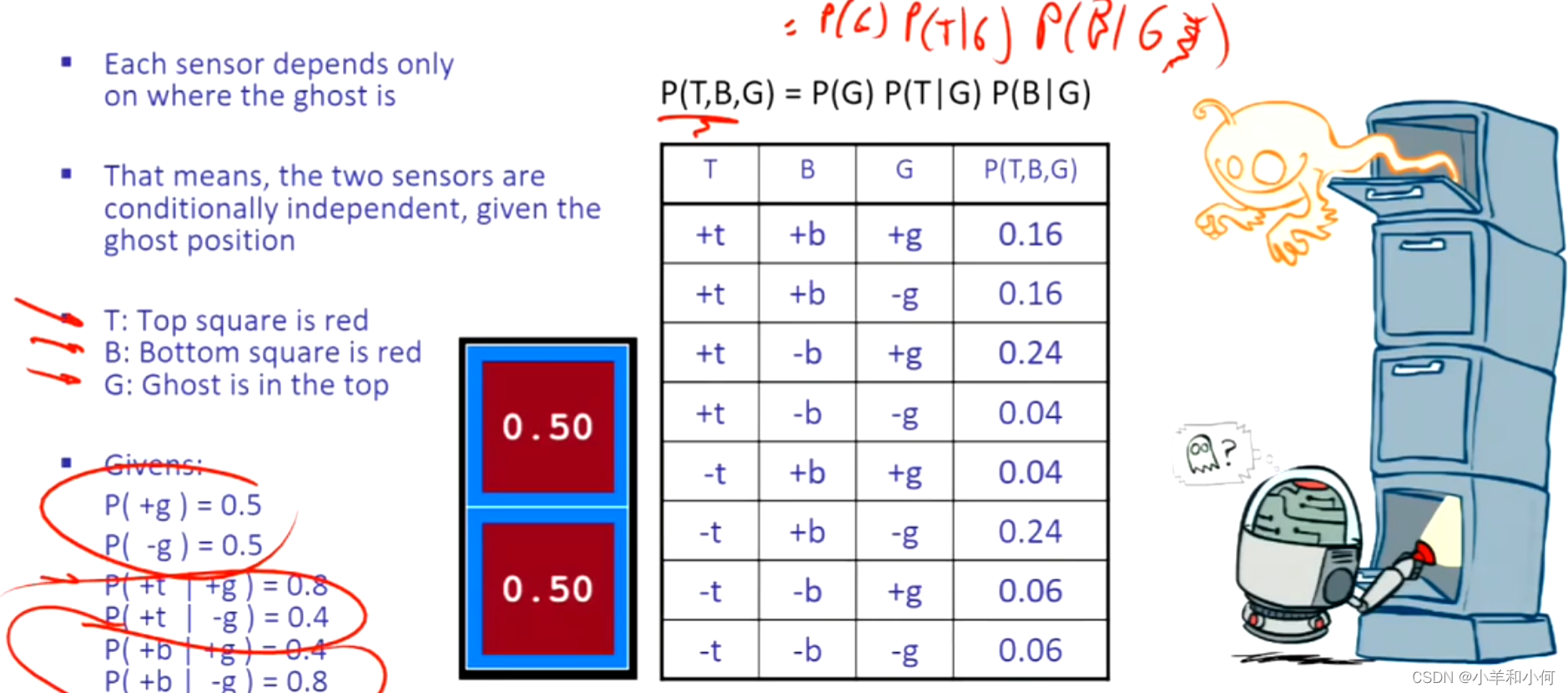
火和警报在给定烟雾的情况下独立：
10.1.2.1 条件独立和链式法则
10.2 贝叶斯网络
贝叶斯网络是一个描述大量变量的复杂分布的工具。其中大的分布由小块组成，这意味着局部相互作用，以及得出这些局部相互作用的产物描述了整个领域的结论所需的假设。
使用完整的联合分布表作为我们的概率模型有两个问题：
- 除非只有几个变量，否则联合分布表太大，无法明确表示。
- 每次从经验上很难学到（估计）超过几个变量的东西
贝叶斯网络：
一种使用简单的局部分布（条件概率）来描述复杂的联合分布（模型）的技术。
- 更恰当地称为图形模型
- 我们描述变量如何进行局部互动。
- 局部的相互作用连锁在一起，产生全局的、间接的相互作用。
例子：
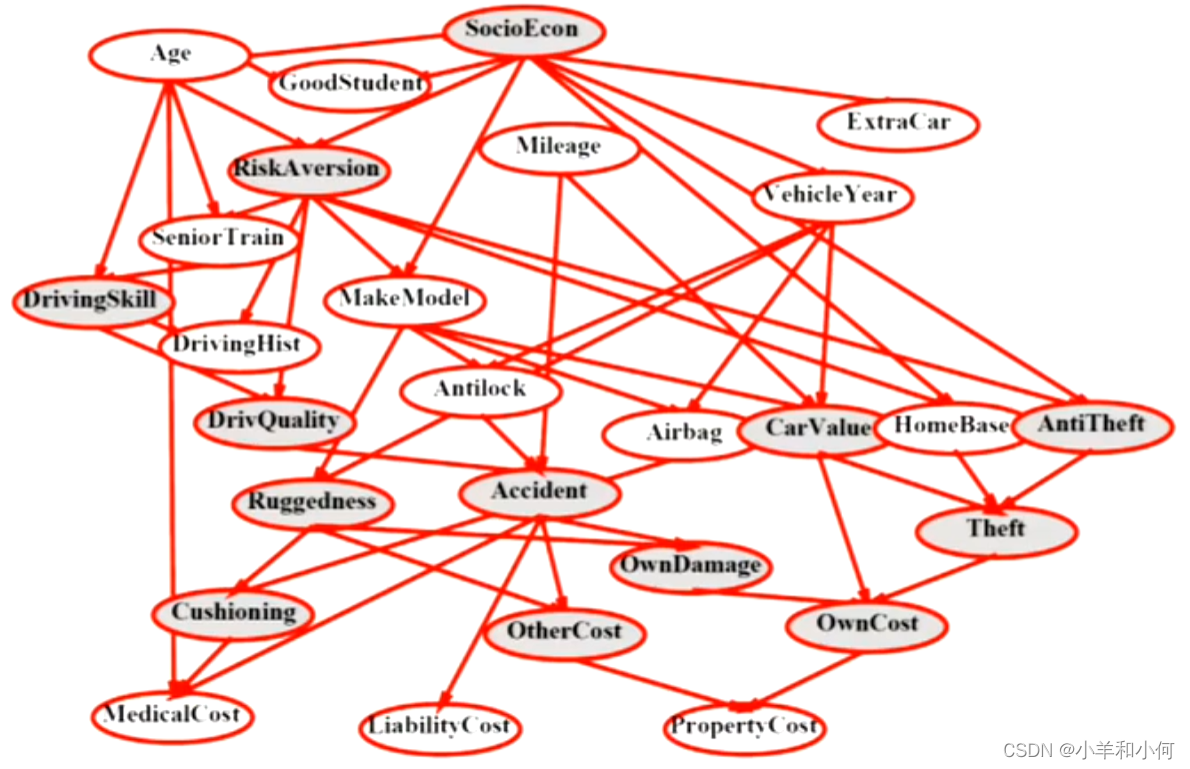
10.2.1 图形化的模型符号
节点：变量（有域）：
- 可以是指定的（观察到的）或未指定的（未观察到的）。
弧：相互作用
- 类似于
约束。
- 表明变量之间的 "直接影响"。
- 形式上：编码有条件的独立性（后面会有更多内容）。
现在：想象一下，箭头意味着直接因果关系（一般来说，它们不是！）。
10.2.2 贝叶斯网络的构建
下面有两个该域上的有效图形模型或贝叶斯网络，但是第二个模型要好一些，因为配备模型2的代理可以做出一些事情，比如看到交通，然后得到关于雨的结论，或者看到雨得到有关交通的结论。
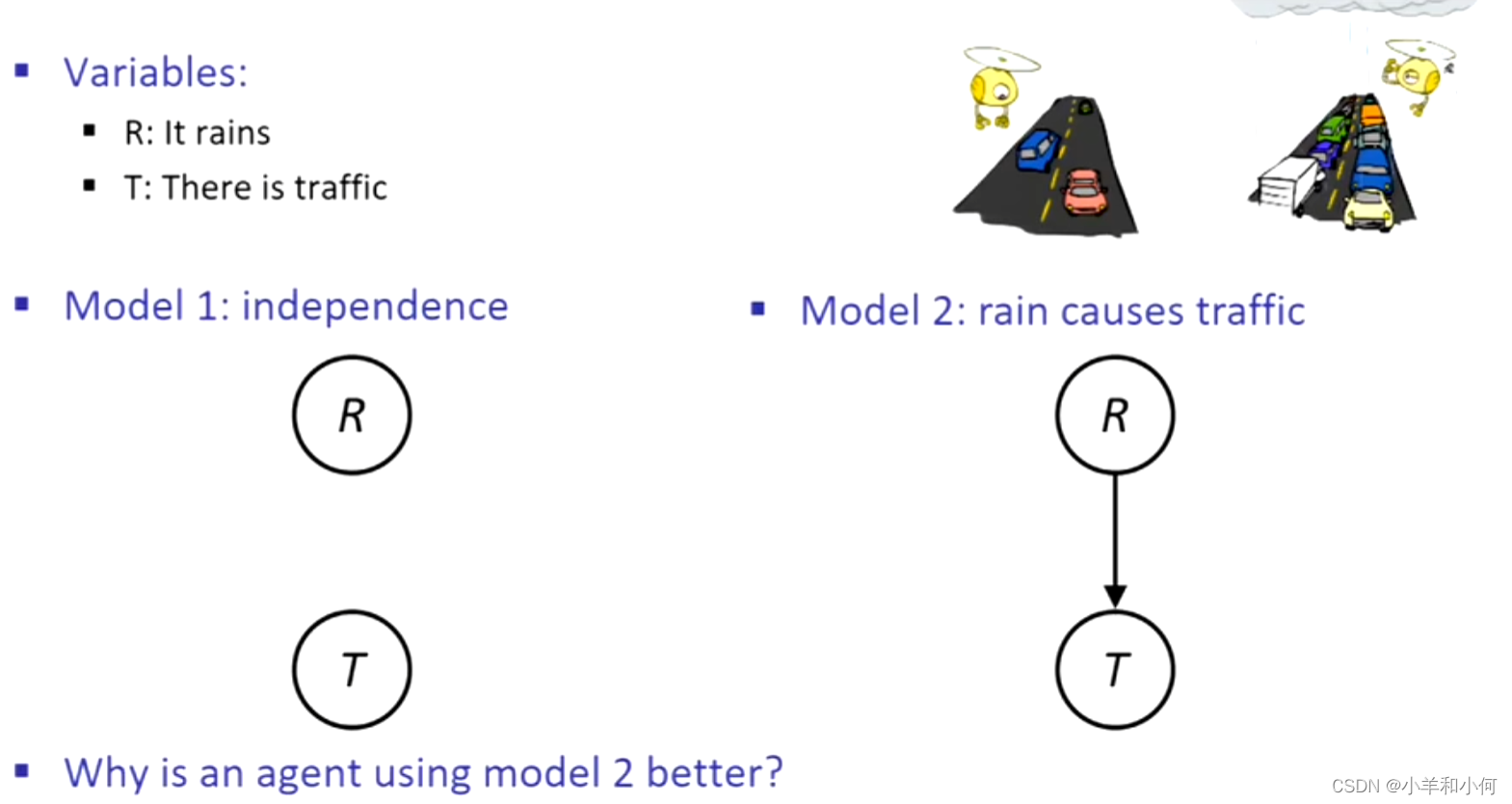
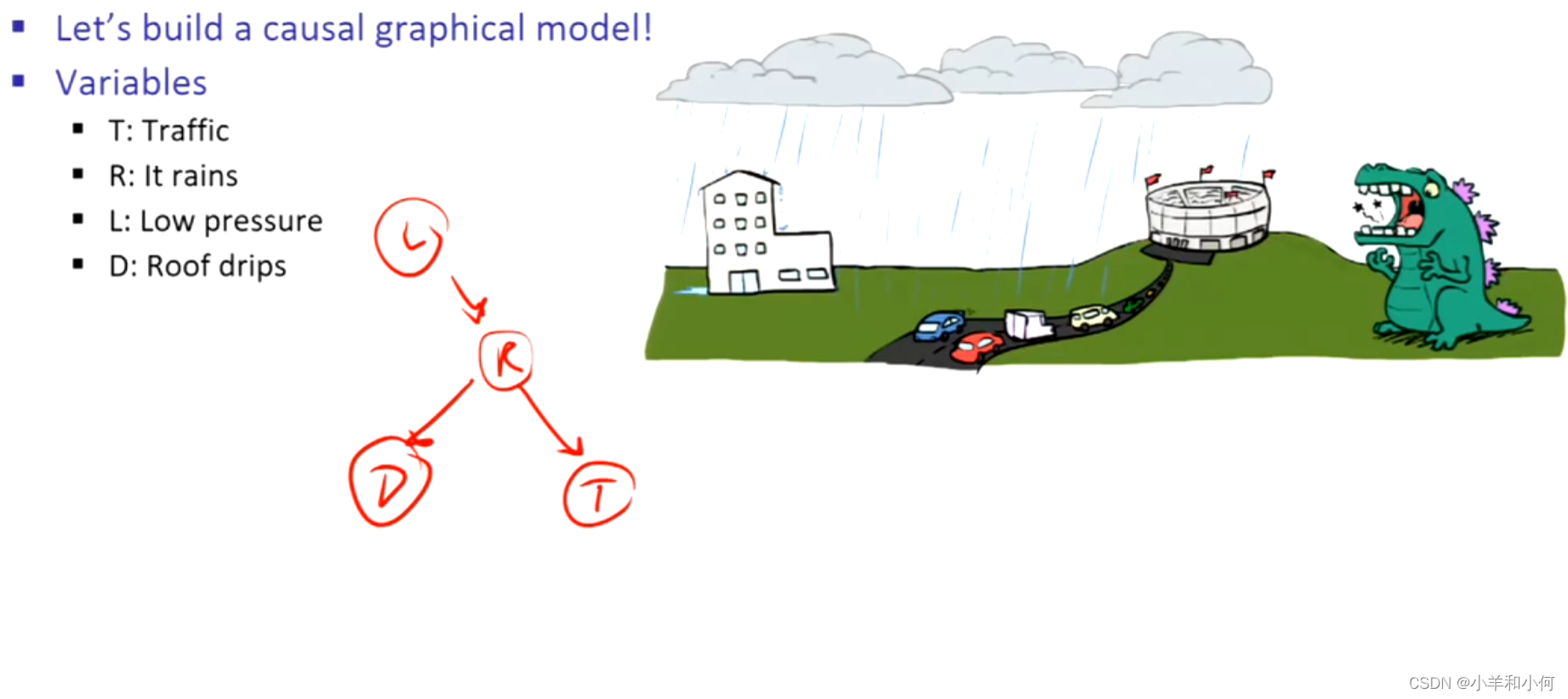
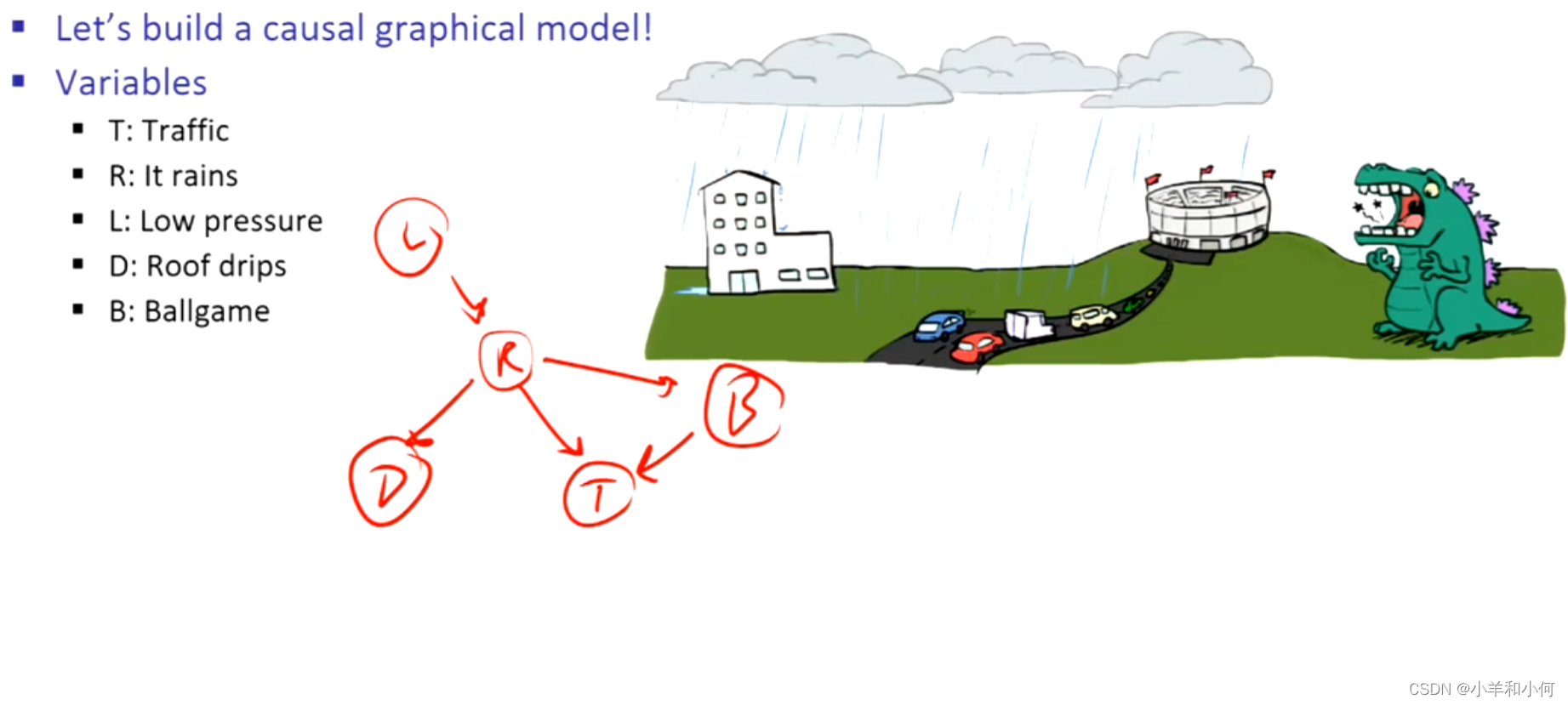
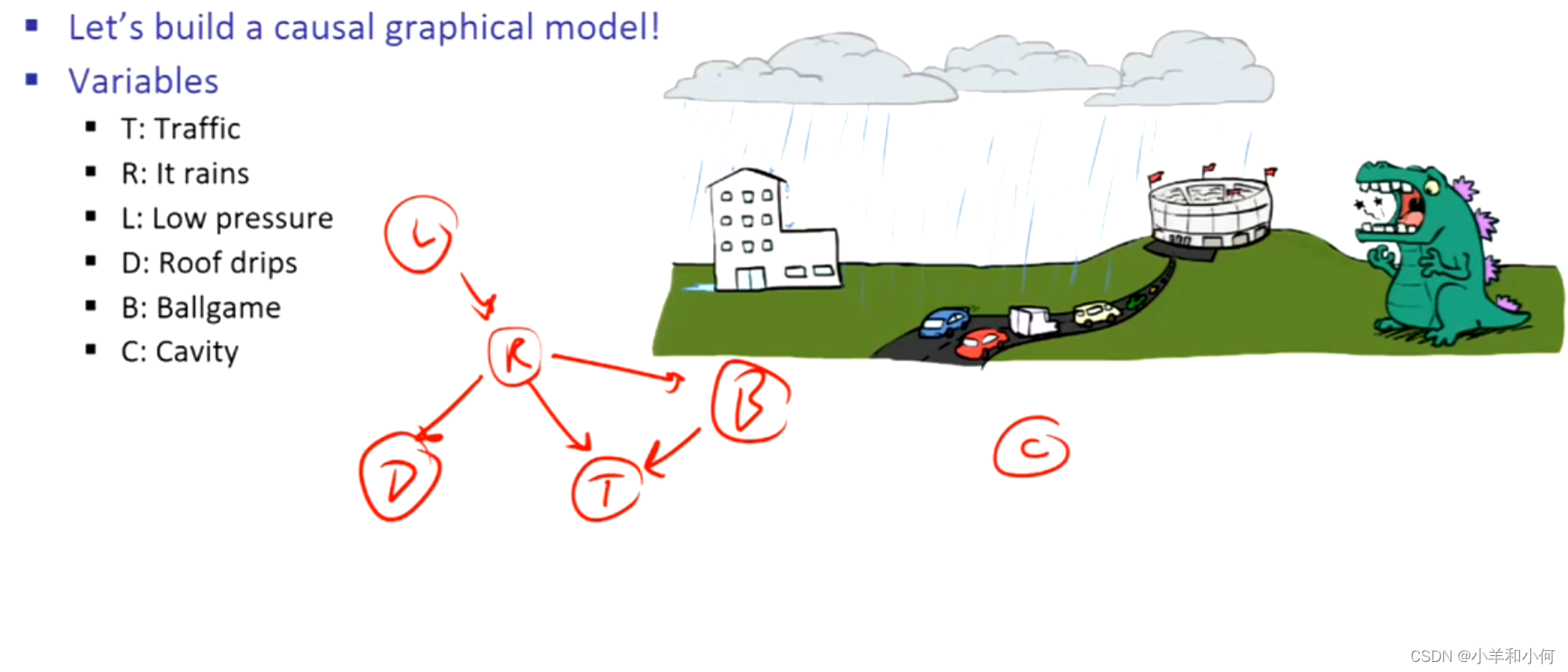
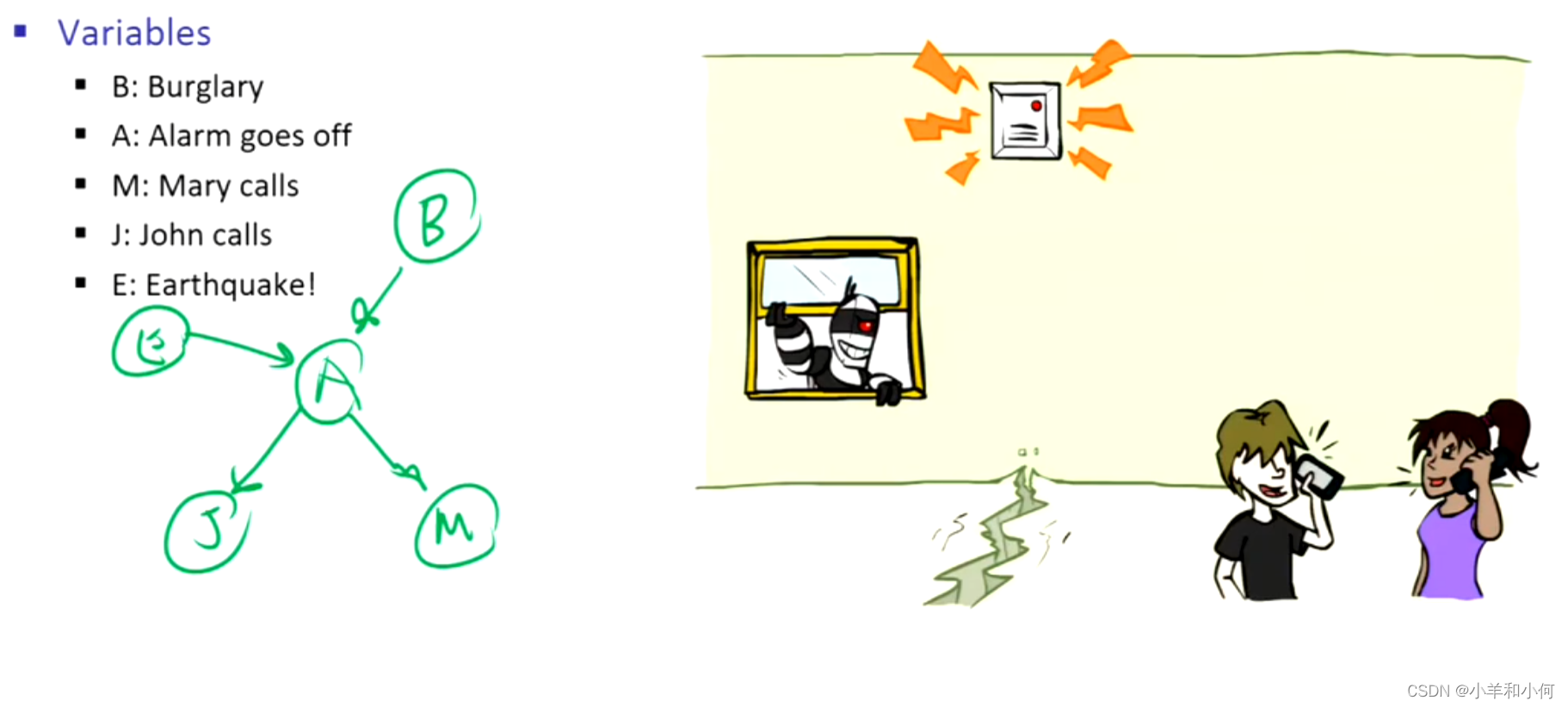
10.2.3 贝叶斯网络的语义
一组节点，每个变量有一个，
一个有向、无环的图，
隐藏在每个节点内部的是条件分布：
- 一组关于
的分布，每个父节点的值的组合都有一个分布
。
：条件概率表。（节点中的东西）
- 描述一个嘈杂的“因果”过程。
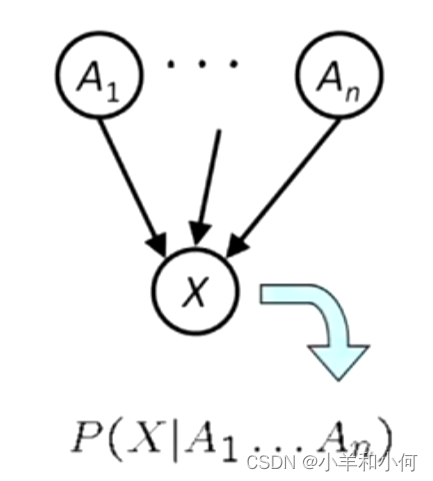
所以贝叶斯网络是一种拓扑结构，意味着一个图加上存在于节点内的小局部条件概率。
10.2.3 贝叶斯网络中的概率
贝叶斯网隐含着对联合分布的编码：
- 作为局部条件分布的乘积。
- 要看一个
给一个完整的分配的概率是多少，把所有相关的条件乘在一起。
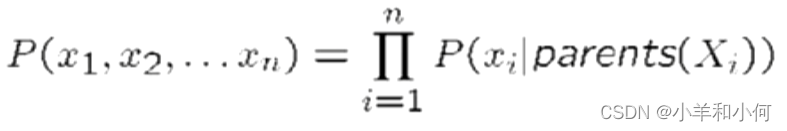
为什么我们能保证设置
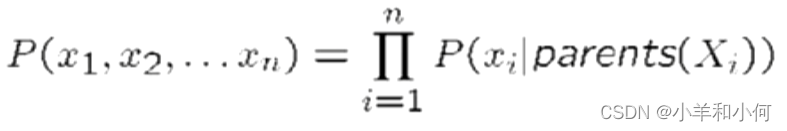
的结果是正确的联合分布？
对于链式法则，公式很相似，但它是：
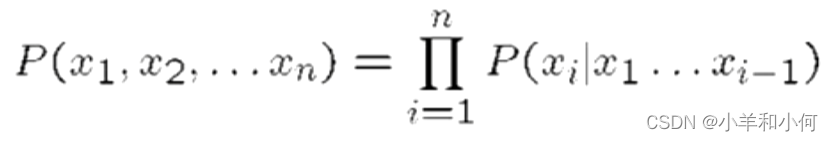
但是我们有条件独立的假设，所以我们的公式为：
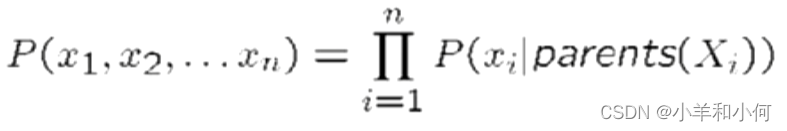
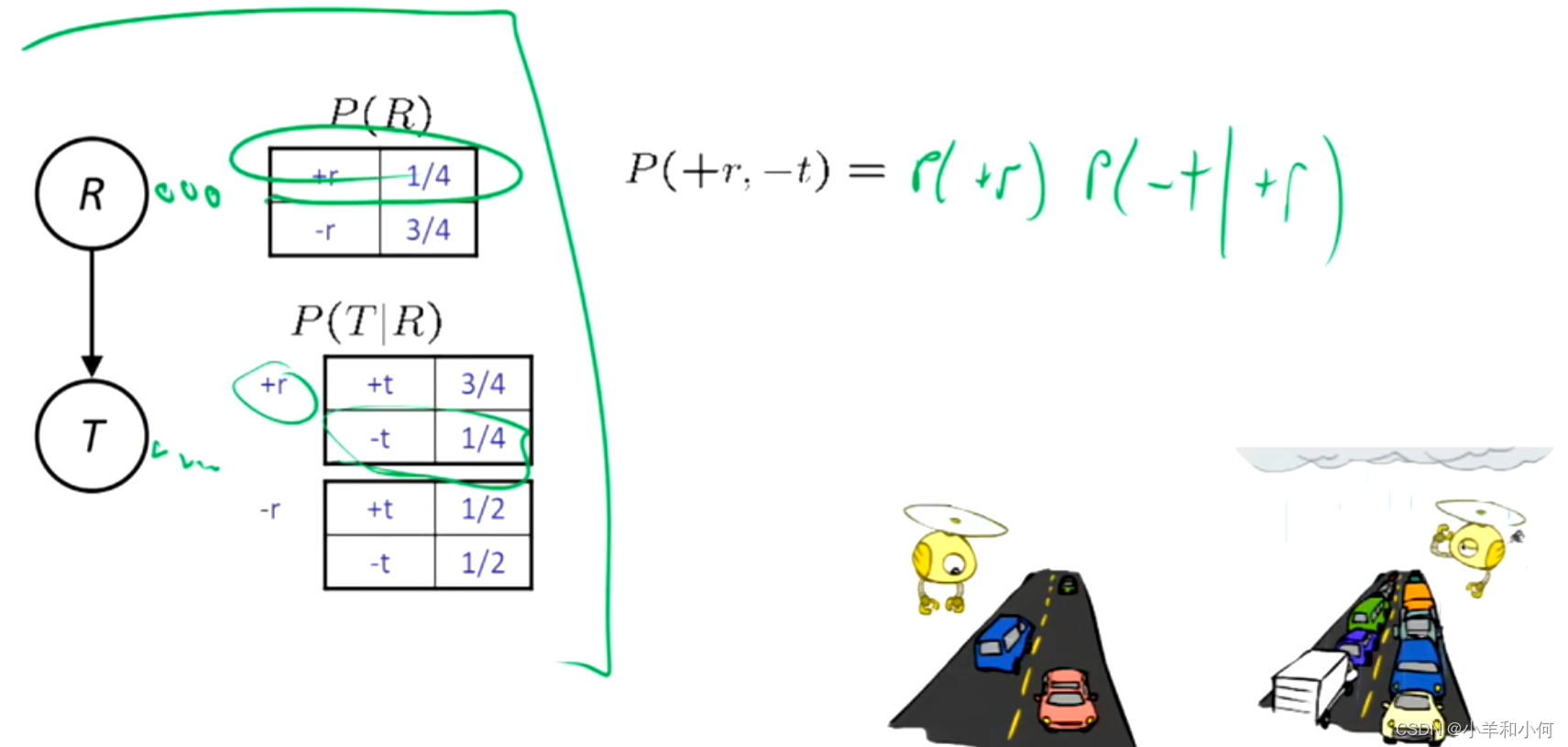
不是每个都能代表每个联合分布：如果我想表示两个变量的联合分布，但不是全部，我们表示的是变量独立的那些，如果我想表示那些不独立的就要有箭头。
- 拓扑结构强制执行某些条件的独立性
例子：
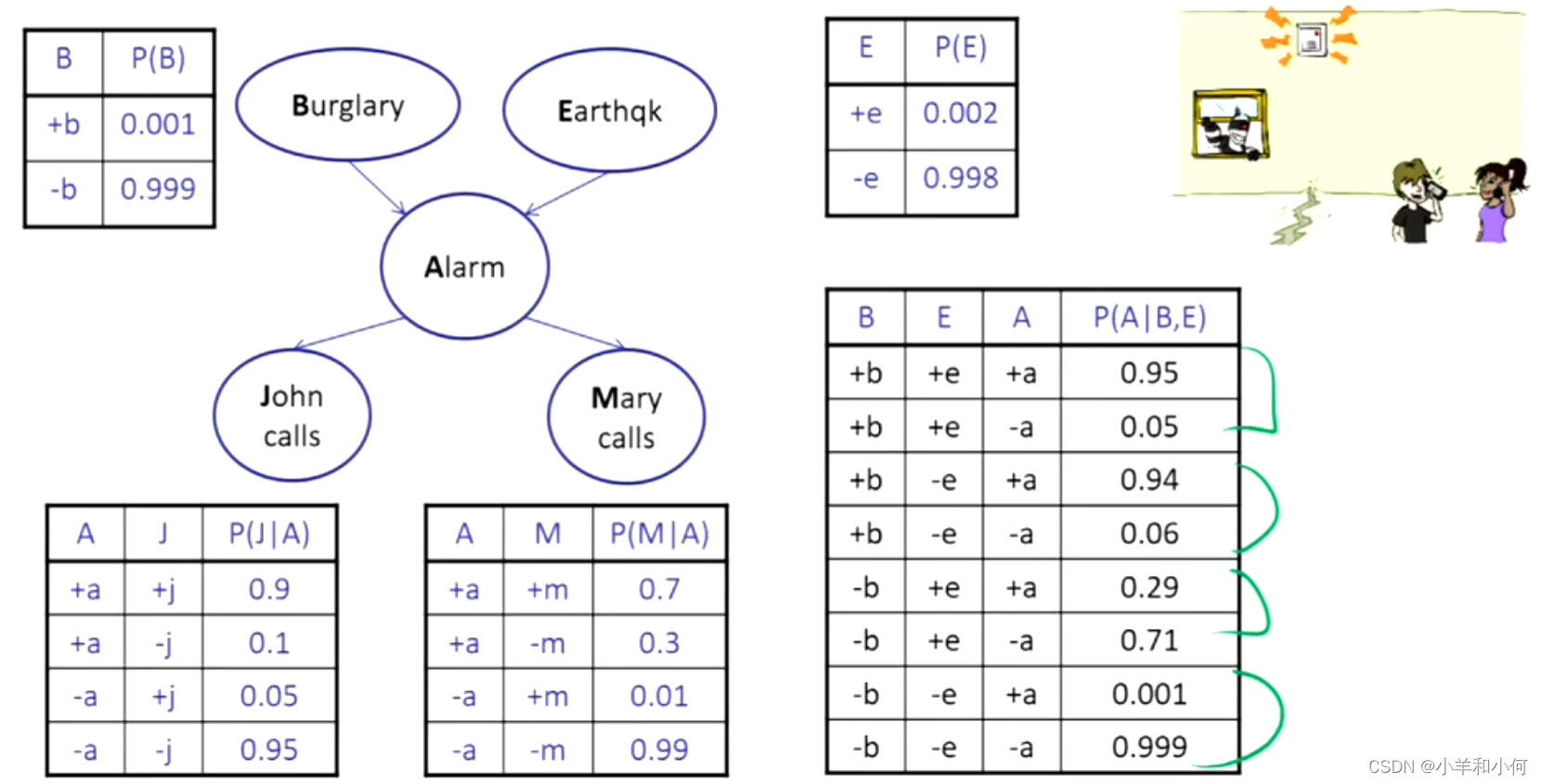
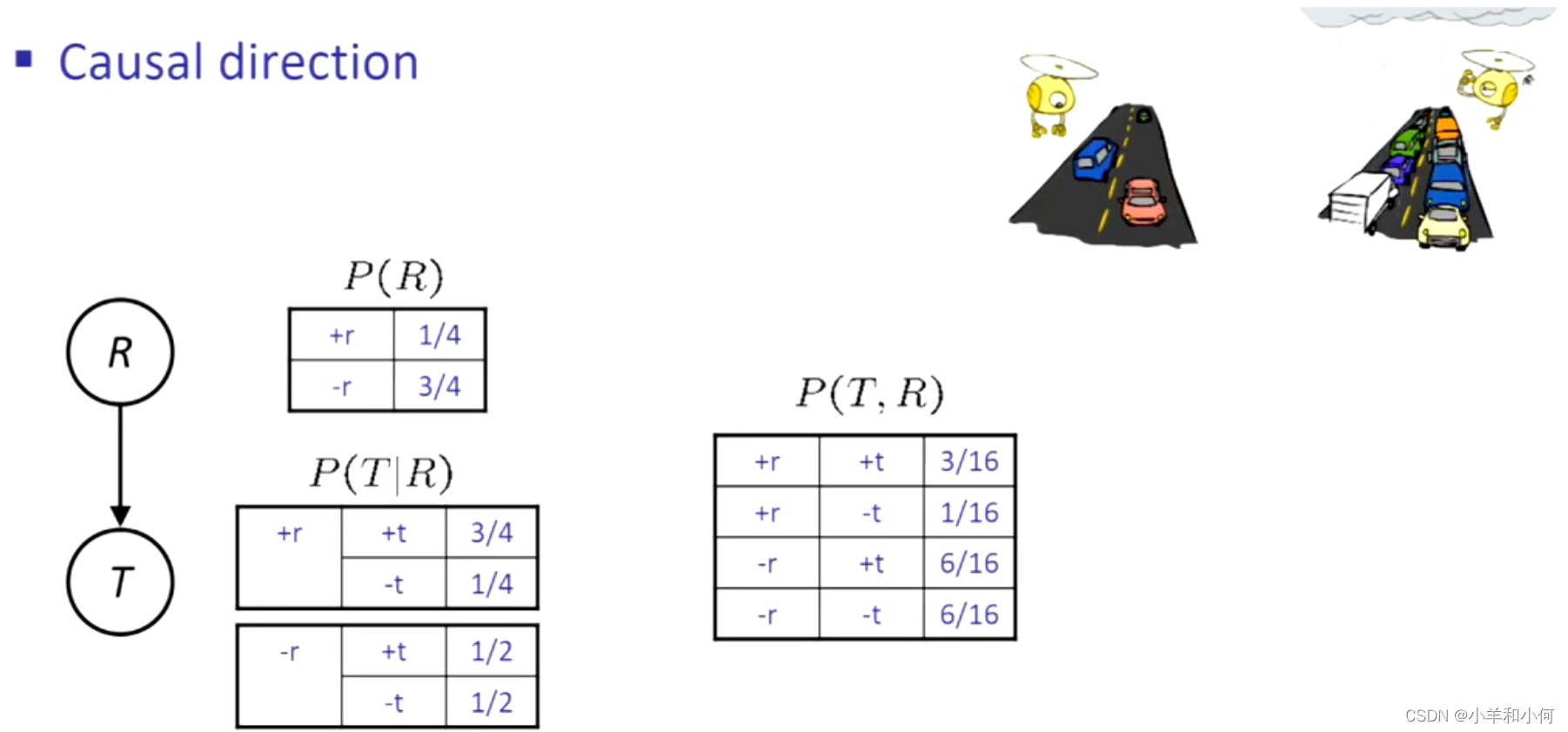
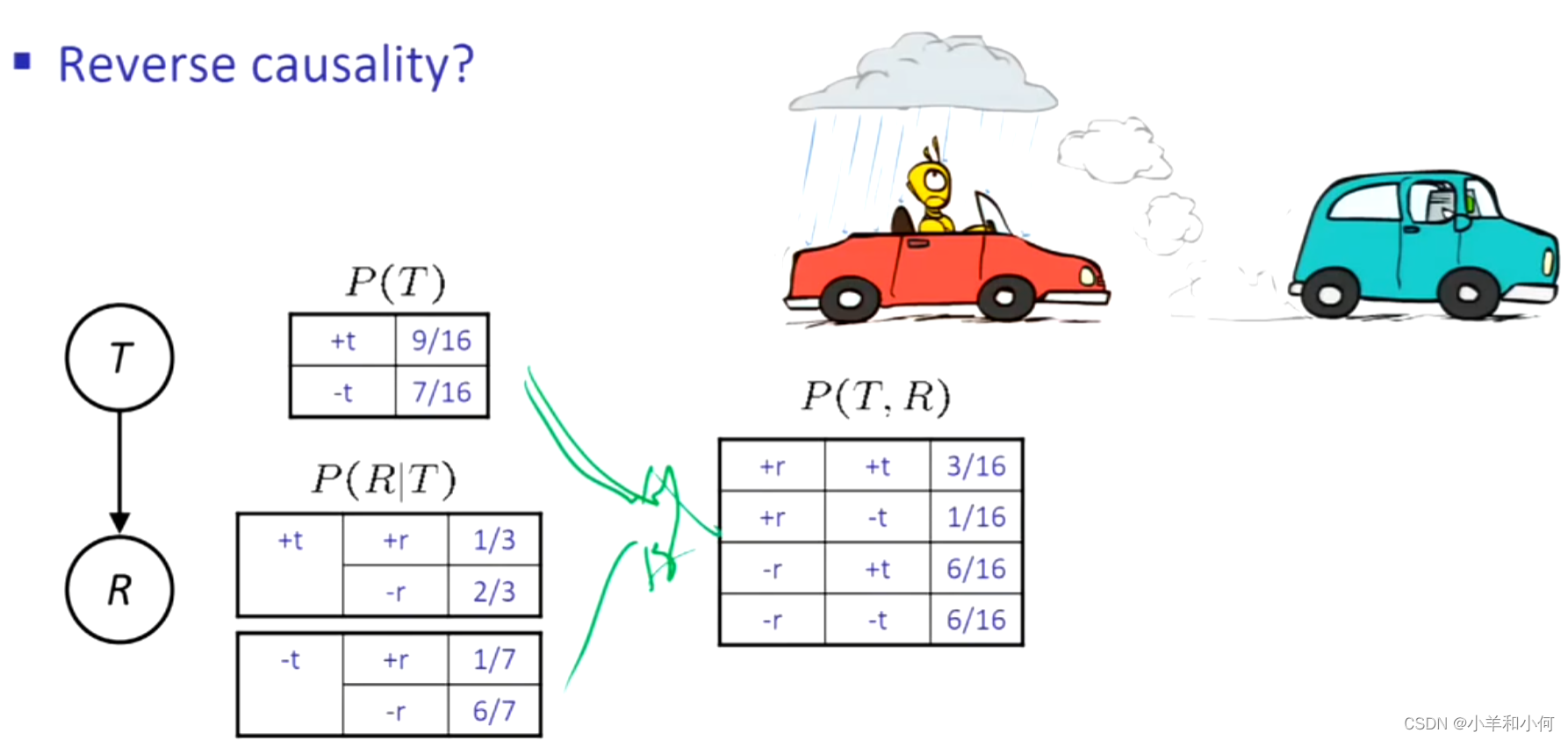
10.2.4 因果关系
当贝叶斯网反映真实的因果模式时：
- 往往更简单（节点有较少的父母）。
- 往往更容易思考。
- 通常更容易从专家那里得到启发。
贝叶斯网不一定真的是因果关系：
- 有时领域中不存在因果网（特别是在变量缺失的情况下）。
- 例如，考虑交通和下雨这两个变量。
- 最终的箭头反映的是相关性，而不是因果关系。
箭头的真正含义是什么？
- 拓扑结构可能刚好编码了因果结构
- 拓扑结构实际上编码了条件独立性
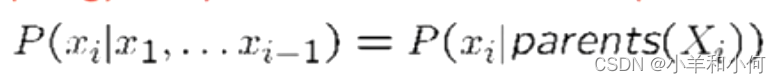
版权归原作者 小羊和小何 所有， 如有侵权，请联系我们删除。