人脸识别AdaFace学习笔记

原文链接：https://openaccess.thecvf.com/content/CVPR2022/papers/Kim_AdaFace_Quality_Adaptive_Margin_for_Face_Recognition_CVPR_2022_paper.pdf

背景

由于人脸图像的模糊和退化，在低质量的数据集中进行人脸识别具有一定的挑战性。如图1所示，低质量人脸图像的缺陷在于当图像退化过大时，会丢失掉相关身份信息，导致无法正常识别。由于在视频监控等场景中经常出现低质量的图像，低质量图像正逐渐成为人脸识别数据集的重要组成部分，如何在训练中利用好这些低质量图像已成为亟需解决的问题。

图1 具有不同图像质量的图像示例

创新点

（1）作者提出了一种基于图像质量自适应的损失函数，该函数能够根据图像质量为不同难度的样本分配不同的权重。

（2）作者观察到角度裕值 (angular margin) 会根据训练样本的难度来对梯度进行缩放。基于这一现象，作者自适应地改变裕值函数以在图像质量高时强调难例样本，如果图像质量低则忽略超难例样本（无法识别的图像）。

（3）作者证明了特征规范化可以表示图像质量，从而无需使用额外的模块来估计图像质量。

相关工作

1、基于裕值的损失函数

将裕值添加到基于softmax loss的损失函数中可以增强学习特征的判别力，经典的方法有SphereFace、CosFace以及ArcFace，通用公式如下：

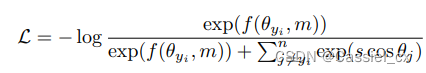
其中， 是特征向量与第 个分类器权重向量之间的夹角， 是 标签的索引， 是裕值，是一个尺度超参数。 是裕值函数，不同损失函数有不同的 ，公式如下：

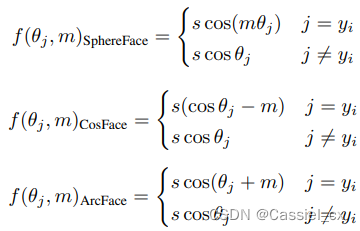
2、自适应损失函数

许多研究已经在训练目标中引入了自适应学习，如 CurricularFace，它在训练的初始阶段将余弦相似度的裕值设置得较小，以便学习简单样本，在训练后期，裕值逐渐增大以学习难例样本。公式如下：

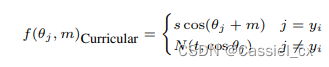
其中，

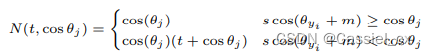
是随着训练进行而逐渐增加的参数。

方法论

对于样本 ，它的 cross entropy-softmax 损失如下：

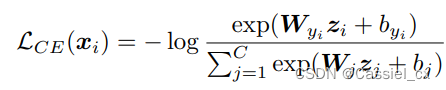
其中， 是样本 的嵌入特征， 是 对应的标签。 是最后一个全连接层权重矩阵的第 j 列， 是对应的偏移值。 是训练集中的样本类别总数。

为了使训练目标直接优化余弦距离，SphereFace 和 NormFace 使用归一化的 softmax，其中偏移值设置为零，并且在训练期间对特征 进行归一化并用 s 进行缩放。 修改后的损失函数如下：

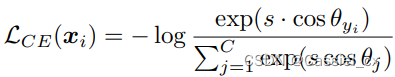
基于上述公式，ArcFace 和 CosFace 在此基础上引入了一个裕值以减少类内变化并增强特征的判别力。

1、裕值和梯度

以前关于基于裕值的 softmax 的工作集中在裕值如何改变决策边界以及它们的几何解释是什么。作者展示了在反向传播期间，角度裕值可以在梯度方程中引入一个附加项，根据样本的训练难度缩放信号。为了证明以上说法，作者展示梯度方程如何随裕值函数变化，

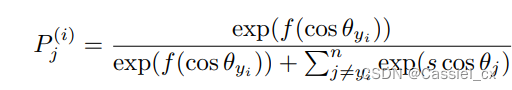
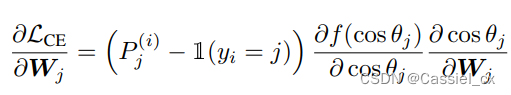
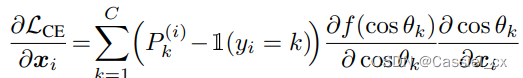
其中， 是对输入 进行 softmax 运算并预测为第 j 类的概率输出，可以将公式中的前两项视为梯度缩放项 (GST) 并表示为：

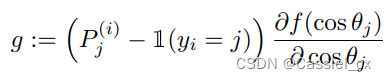
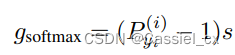
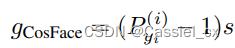
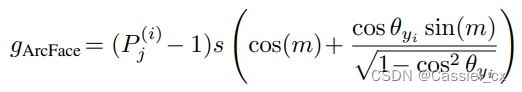
因为 GST 是关于 和 的函数，那么则可以根据训练难度 () 对不同的样本分配不同的权重。

在图3中， 和 分别表示不带和带有裕值的决策边界，简单样本会靠近 （正确分类），而困难样本则会靠近 （错误分类）。弧线里面的颜色代表了 GST 的大小，深红色区域的样本对训练的贡献更大，裕值只影响决策边界的位置，而不影响 GST 的大小。然而，正角度裕值不仅会移动决策边界的位置，还使得决策边界附近的 GST 较大、远离决策边界位置的 GST 较小，因此没有利用好难例样本。AdaFace则基于特征范数值自适应地改变裕值函数，当范数较大时，会对远离决策边界的样本分配较大的权重，当范数较低时，则强调靠近决策边界的样本。

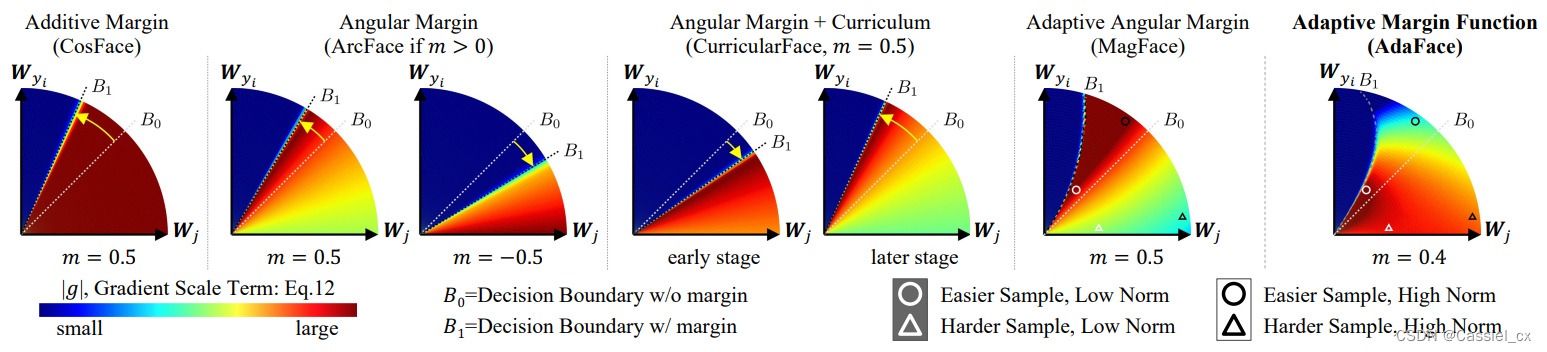
图3 不同裕值函数及其在特征空间上的GST

2、规范化和图像质量

图像质量是一个综合术语，涵盖了亮度、对比度和清晰度等特征。 图像质量评估 (IQA) 在计算机视觉中得到了广泛的研究。在 AdaFace 中，无需引入一个额外的模块来计算图像质量，而直接使用特征范数 (feature norm) 来表示图像质量，特征范数与图像质量密切相关，如图4所示。从图4(a)可以看出，特征范数与图像质量之间的相关性大于概率输出与图像质量之间的相关性。

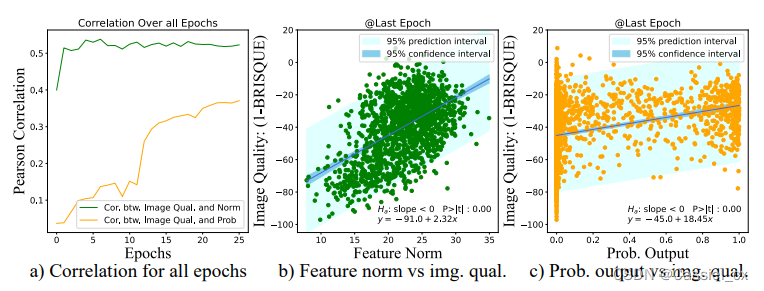
图4 a)各变量间的皮尔逊相关系数图；b)特征范数与图像质量之间的散点图；c)概率输出与图像质量之间的散点图

3、基于特征范数的自适应裕值(AdaFace)

为了解决无法识别的图像引起的问题，AdaFace 基于特征范数来调整裕值函数。此外，由于裕值函数可以改变决策边界的位置，因此可以利用裕值函数来强调样本的不同训练难度。

作为特征范数， 是模型相关量，作者使用批量统计值 和 对特征范数进行归一化，公式如下：

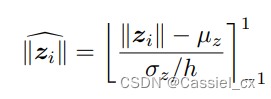
其中， 和 分别是在一个 batchsize 内，所有 的均值和标准差。作者将上式的输出范围限制在-1到1之间。 为0.33，使得 尽可能在 [-1,1] 之间。

此外，如果训练时的 batchsize过小， 和 可能会不太稳定，因此使用指数滑动平均 (EMA) 来稳定批处理统计信息 和 ，公式如下：

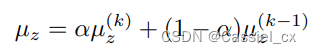
其中， 表示第 次迭代优化， 是一个值为0.99的动量。 公式同上。

AdaFace 损失函数满足以下两个要求：1) 如果图像质量高，则强调难例样本，2）如果图像质量低，则不强调难例样本。作者通过两个自适应项 和 来实现上述功能，这两项分别对应角度裕值和附加裕值。AdaFace 损失函数的公式如下：

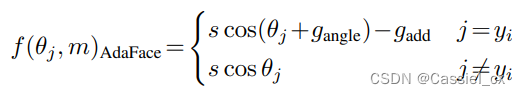
其中， 和 是关于图像质量指标 () 的函数，它们的定义如下：

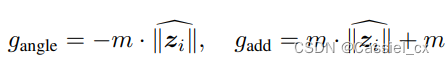
注意到，当 = -1 时，损失函数变成了 ArcFace；当 = 0 时，则变成了 CosFace；当 = 1 时，变成了带有偏移量的负角度裕值。这样，当特征范数较高时，将在远离决策边界的地方获得更高的梯度尺度，而当特征范数较低时，将在决策边界附近获得更高的梯度尺度。 对于低范数特征，远离边界的难例样本被淡化。

实验结果

表1 对各超参数进行的消融实验结果

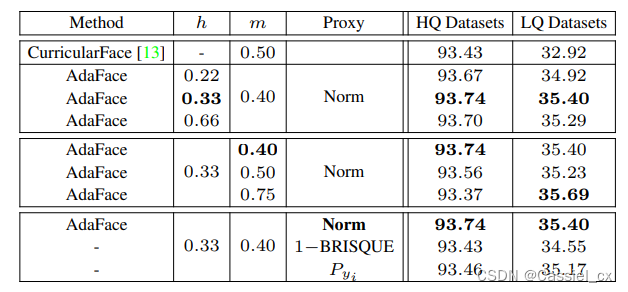
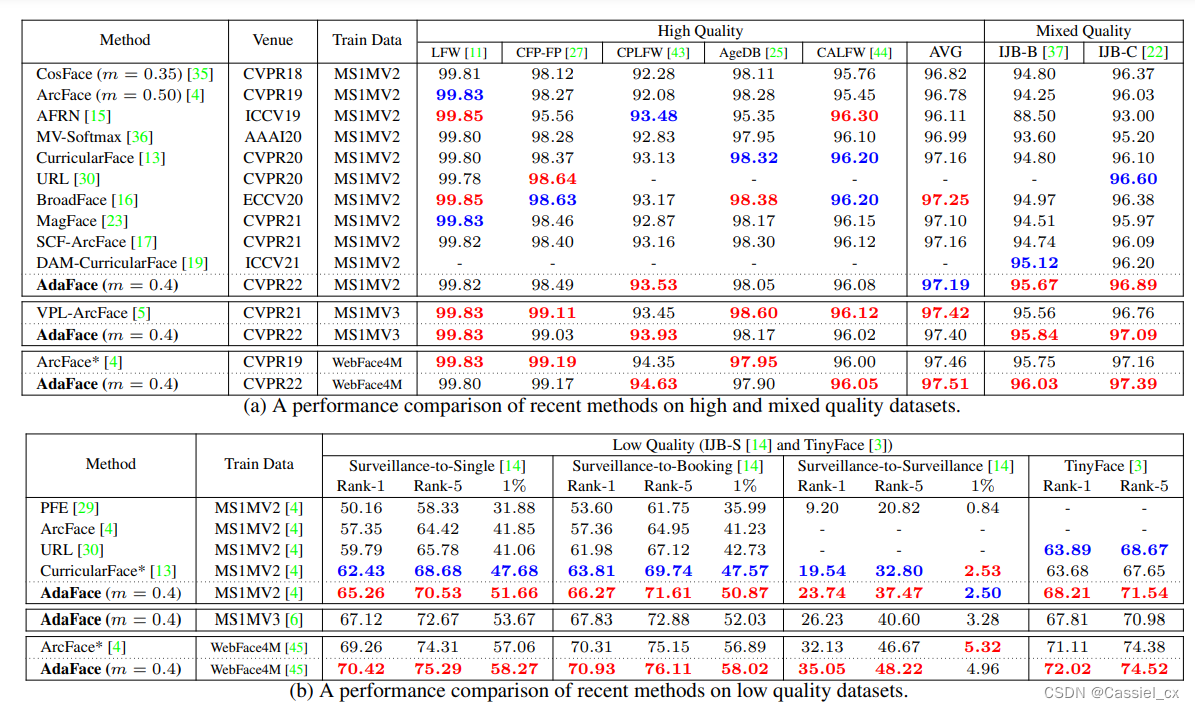
表2 在不同图像质量的数据集中与 SoTA 方法的比较