手搓人工智能—聚类分析（下）谱系聚类与K-mean聚类

“无论结果如何，至少我们存在过”

——《无人深空》

前言

    除了上一篇手搓人工智能-聚类分析（上）中提到的两种简单聚类方式，还有一些更为常用、更复杂的聚类方式：谱系聚类，K-均值聚类。

谱系聚类

    谱系聚类又被称为是系统聚类，层次聚类，它的思想主要来源于社会科学和生物分类学，目标不仅是要产生样本的不同聚类，而且要生成一个完整的样本分类谱系。

谱系聚类合并算法

    先给出一般谱系聚类算法：

• 初始化：每个样本作为一个单独的聚类，
• 循环，直到所有样本属于一个聚类为止： - 寻找当前聚类中最相近的两个聚类：- 删除聚类 和 ，增加新的聚类
• 输出：样本的合并过程，形成层次化谱系

    但是，对于一个聚类问题来说，将所有样本合并为一个聚类的结果显然是毫无意义的。我们可以设置一个终止条件，当满足该条件时，输出当前的聚类。常用的终止条件包括

• 预定类别数：预先设定一个目标聚类数，当合并过程中剩余的聚类数量达到预定的目标聚类数时，停止合并。
• 距离阈值：预先设定一个距离阈值，当最近的两个聚类之间的距离大于阈值时，停止合并过程，输出当前的聚类。
• “最优”聚类数：在合并过程中按照某种准则判断当前的聚类结果是否达到“最优”的聚类数，以“最优”聚类数作为终止合并的条件。依据什么样的准则确定一个给定样本集的“最优”聚类是大多聚类分析方法需要面对的问题。根据样本间距离准则，有 - 最大距离法：以两个聚类 和 中相距最远的两个样本间距离度量聚类之间的相似程度 - 最小距离法：以两个聚类 和 中相距最近的两个样本间距离度量聚类之间的相似程度 - 平均距离法：计算两个集合中任意一对样本的距离，以所有的距离平均值来度量集合之间的相似程度 - 平均样本法：以两类样本均值之间的距离度量集合之间的相似程度

    算法在第 K 轮合并之前需要计算 ![n-k+1](https://latex.csdn.net/eq?n-k+1) 个聚类之间的距离，生成整个谱系需要 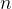![n](https://latex.csdn.net/eq?n) 轮合并，因此总的距离计算次数是：

    在具体实现过程中，可以利用距离矩阵 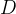![D](https://latex.csdn.net/eq?D) 来记录当前各个聚类之间的距离，通过寻找其中的最小元素来确定下一步进行合并的两个聚类；合并聚类后更新距离矩阵 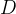![D](https://latex.csdn.net/eq?D)，根据所用不同距离度量方式计算新生成聚类与其他聚类之间的距离

    优化后的算法流程如下：

• 初始化：每个样本作为一个单独的聚类，，每个聚类的样本数：，计算每个样本间的距离，构成距离矩阵 ，聚类数
• 循环，直到满足聚类的终止条件为止： - 寻找距离矩阵 中上三角矩阵元素的最小值 - 删除聚类 ，增加新的聚类 - 更新距离矩阵
• 输出：聚类，聚类数

示例代码（C++）

采用距离度量为欧式距离，取最小距离

void Clustering::Lineageclustering(std::vector<std::vector<double>> sample, double theta, const char* type, int p)
{
    Distance distance;
    std::vector<std::vector<double>> Distancemartix;
    std::vector<std::vector<double>> centers;
    //初始化
    for (int i = 0; i < sample.size(); i++) {
        clusters.push_back(std::vector<std::vector<double>>());
        clusters[i].push_back(sample[i]);
    }
    Distancemartix = distance.DistanceMartix(sample, type, -1);
    //遍历每个样本
    double min = 0;
    while (min < theta) {
        //更新聚类中心
        for (int m = 0; m < clusters.size(); m++) {
            centers.push_back(GetCenter(clusters[m]));
        }
        //找到最近的两个聚类，并合并聚类
        min = DBL_MAX;
        int select_index1 = 0;
        int select_index2 = 0;
        for (int i = 0; i < centers.size(); i++) {
            for (int j = i; j < centers.size(); j++) {
                if (i == j) continue;
                min = (min < distance.SelectDistance(centers[i], centers[j], type, p)) ? min : distance.SelectDistance(centers[i], centers[j], type, p);
                select_index1 = (min < distance.SelectDistance(centers[i], centers[j], type, p)) ? select_index1 : i;
                select_index2 = (min < distance.SelectDistance(centers[i], centers[j], type, p)) ? select_index2 : j;
            }
        }
        for (int i = 0; i < clusters[select_index2].size(); i++) {
            clusters[select_index1].push_back(clusters[select_index2][i]);
        }
        clusters.erase(clusters.begin() + select_index2);
        if (centers.size() < 2) {
            break;
        }
    }
}

输入测试样本 ,阈值设为2

data = { {1, 1}, {1, 3}, {3, 5}, {3, 3}, {3, 7}, {3, 9} };

分类结果

Cluster 0: (1, 1)
Cluster 1: (1, 3)
Cluster 2: (3, 5)
Cluster 3: (3, 3)
Cluster 4: (3, 7) (3, 9)

K-mean 聚类

    K-均值算法的想法最早由 Hugo Steinhaus 于 1957 年提出，Stuart Lloyd 于 1957 年在 Bell 实验室给出了标准K-均值聚类算法。由于算法实现简单，计算复杂度和存储复杂度低，对很多简单的聚类问题可以得到令人满意的结果，K-均值算法已经成为最著名和常用的聚类算法之一

K-mean 算法的目标是将 个样本依据最小化类内距离的准则分到 K 个聚类之中

直接对上述类内距离准则优化存在一定困难，不妨换一个思路：

首先假设每个聚类的均值 是固定已知的，那么这个优化问题就很容易求解了

现在这个问题变成了：

每一个样本 选择加入一个聚类 ，使得类内距离准则最小

很显然，如果 ，应该将样本 放入聚类 ，这样可以使得 最小。

然而，已知每个聚类的均值 的假设是不成立的，因为在知道每个聚类包含哪个样本之前是无法求得样本均值的，聚类的均值只能根据这个聚类中所有样本求得。

K-均值的思想是首先对每类均值做出假设 ，得到对聚类结果的猜想 ，将样本分类后更新均值，得到一个迭代的过程

经过多轮迭代，分类结果不再发生变化，可以认为算法收敛到了一个对 的优化结果

K-mean 聚类算法

K-mean算法流程

• 初始化：随机选择K个聚类均值
• 循环，直到K个均值不在变化为止 - - for i = 1 to n - - 更新 K 个聚类的均值： -
• 输出：聚类

示例代码（C++）

struct Point {
    std::vector<double> coordinates;
};

// 计算两个数据点之间的欧氏距离
double distance(const Point& p1, const Point& p2) {
    double sum = 0.0;
    for (size_t i = 0; i < p1.coordinates.size(); ++i) {
        sum += std::pow(p1.coordinates[i] - p2.coordinates[i], 2);
    }
    return std::sqrt(sum);
}

// K-means聚类算法
std::vector<int> kMeans(const std::vector<Point>& data, int k, int maxIterations) {
    std::vector<int> labels(data.size(), 0); // 存储每个数据点的簇标签
    std::vector<Point> centroids(k); // 存储簇中心

    // 随机初始化簇中心
    std::srand(std::time(0));
    for (int i = 0; i < k; ++i) {
        int randomIndex = std::rand() % data.size();
        centroids[i] = data[randomIndex];
    }

    for (int iteration = 0; iteration < maxIterations; ++iteration) {
        // 分配数据点到最近的簇中心
        for (size_t i = 0; i < data.size(); ++i) {
            double minDist = std::numeric_limits<double>::max();
            int closestCentroid = 0;
            for (int j = 0; j < k; ++j) {
                double dist = distance(data[i], centroids[j]);
                if (dist < minDist) {
                    minDist = dist;
                    closestCentroid = j;
                }
            }
            labels[i] = closestCentroid;
        }

        // 更新簇中心
        std::vector<int> count(k, 0);
        std::vector<Point> newCentroids(k, {std::vector<double>(data[0].coordinates.size(), 0.0)});
        for (size_t i = 0; i < data.size(); ++i) {
            int clusterIndex = labels[i];
            count[clusterIndex]++;
            for (size_t j = 0; j < data[i].coordinates.size(); ++j) {
                newCentroids[clusterIndex].coordinates[j] += data[i].coordinates[j];
            }
        }
        for (int i = 0; i < k; ++i) {
            for (size_t j = 0; j < data[0].coordinates.size(); ++j) {
                centroids[i].coordinates[j] = newCentroids[i].coordinates[j] / count[i];
            }
        }
    }

    return labels;
}